Методические указания к курсовому проектированию по курсу Проектирование систем электрификации идипломному проектированию по курсу

• Название: Методические указания к курсовому проектированию по курсу Проектирование систем электрификации идипломному проектированию по курсу
• Дата: 28.03.2022
• Размер: 3.43 Mb.
• Имя файла: Dok_PROKT_E-FIKATsII_soft_Word.doc
• Тип: Методические указания; #420913
• страница: 30 из 31

.

При использовании уголков для вертикальных электродов в качестве диаметра принимаем эквивалентный диаметр уголка:

d = d_ЕР = 0,95  b.

где b ширина полки равнобокого уголка.

Для уголка с шириной полки b=0,06 [ м ]:

d= 0,95  b= 0,95  0,06 = 0,057 [ м ],

Находим сопротивление растеканию одного вертикального электрода: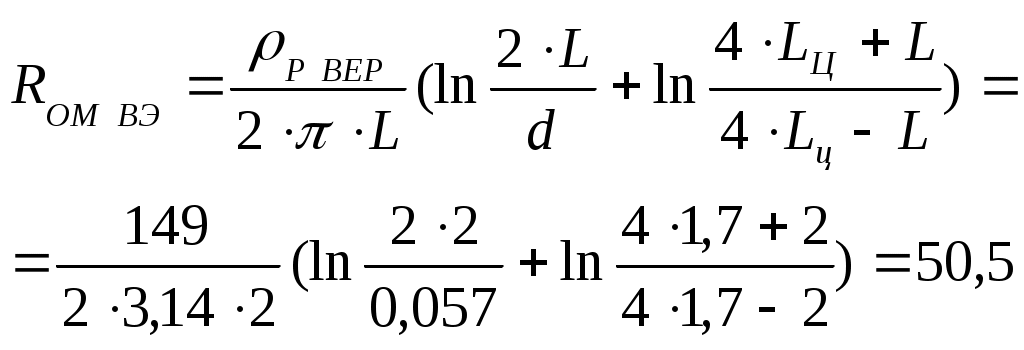

. [ Ом ]

Определяем примерное количество вертикальных заземлителей при предварительно принятом коэффициенте использования. Коэф­фициент использования вертикальных электродов в случае размеще­ния их по контуру без учета влияния горизонтальных электродов связи находим по справочным данным. Отношение расстояния между вертикальными электродами А = 4 [ м ] к их длине L = 2 [ м ]: (А / L ) = ( 4 / 2 ) = 2.

Используя справочные данные, выбираем предварительно коэф­фициент использования: k _{И В} = 0,66 (при числе уголков порядка 60 и отношении (А / L ) = ( 4 / 2 ) = 2 ). Примерное число n вертикальных заземлителей :

n = [R_{ОМ ВЭ} / ( k _{И В}  R_И)];

где R_И  необходимое сопротивление искусственного заземлителя [ Ом ] .

Находим примерное число n вертикальных заземлителей :

n = [R_{ОМ ВЭ} / ( k _{И В}  R_И)] = [ 50,5 / ( 0,66  1,33 )] = 57,5;

округляем до ближайшего большего значения;  необходимое число вертиакальных зазаемлителей, расположенных по контуру заземления равно n = 58.

Определяем сопротивление, оказываемое току горизонталь­ным заземлителем, состоящий из полос b x h = 40 x 4 мм, приваренных к верх­ним концам уголков. Коэффициент использования горизонтальной соединительной полосы в контуре заземления: k _{И Г} = 0,28 (при числе уголков 60 и отношении расстояния между вертикаль­ными электродами к их длине (А / L ) = ( 4 / 2 ) = 2.

Сопротивление полосы:

.

Расположение горизонтально протяженного заземлителя ниже уровня земли показано на рисунок 11.8.

LЦ L h Рисунок 11.8  Горизонтальный эаземлитель

Расстояние между вертикальными электродами D= 4 м. Предпола­гаемое количество электродов 60, тогда периметр периметр контура зазаемления, то которому прокла­дываются горизонтальные полосы, будет составлять L_ПК = 58  4 = 232 м.

Находим сопротивление горизонтального контура периметромL_ПК = 232 м. :

. Ом

Уточненное сопротивление вертикальных электродов:

. [ Ом ]

Уточненное число вертикальных электродов определяем при коэф­фициенте использования k_ИВ = 0,58, при числе уголков 60 и отношении расстояния между вертикаль­ными электродами к их длине (А / L ) = ( 4 / 2 ) = 2:

n = [R_{ОМ ВЭ} / ( k _{И В}  R_И)] = [ 50,5 / ( 0,58  1,64 )] = 53,1;

Окончательно принимаем к установке 58 вертикальных уголка, расположенных по контуру РП.

Изменение потенциала в пределах площадки, на которой размеще­ны электроды заземлителя, происходит плавно; при этом напряжение прикосновения U_ПРи напряжение шага U_Шимеют небольшие значения по сравнению с потенциалом заземлителя ₃. Однако за пределами контура по его краям наблюдается крутой спад ₃. Чтобы исключить в этих местах опасные напряжения шага, которые особенно высо­ки при больших токах замыкания на землю, по краям контура, за его пределами, в первую очередь в местах проходов и проездов, укладыва­ют в землю на различной глубине дополнительные стальные полосы, соединенные с заземлителем. Благодаря этому спад потенциала в этих местах происходит по пологой кривой.

Дополнительно к контуру заземления из вертикальных заземлителей, связанных горизонтальной полосойна территории распределительной подстанции устанавливается сетка из полос на расстоянии 0,8 – 1, 0 м от оборудования с шагом 0,8 – 1, 0 м, с попнрнчными связями через 6 м . Эти не учтенные расчетом электроды уменьшают общее сопротивление заземления, точно так же, как и дополнительные вертикальные электроды (58 вместо 54).

Проверяем термическую стойкость полосы b x h = 40 x 4 мм. Минимальное сечение S [ мм² ] полосы из условия термической стойкости при коротком замыкании на землю определяется из выражения:

,

где I_РАСЧ = 1,24 [ кА ]  расчетный ток через проводник;

t_ПР = 1,25 [ с ]  приведенное время протекания тока короткого замыкания на землю;

С_СТАЛЬ = 74 – постоянная, зависящая от материала электрода заземлителя и заземляющего проводника.

Подставляем значения::

. [ мм² ]

По результатам расчетов полоса S = b x h = 40 x 4 = 160 [ мм² ] > 18,7 [ мм² ] условия термической стойкости удовлетворяет.


12 Задачи на компенсацию реактивной мощности

12.1 Условия задач на компенсацию реактивной мощности
Задача № 1 .

Освещение помещения выполнено люминесцентноыми лампами ЛБ – 40

(мощностью по Р_Л = 40 [ Вт ] каждая). Потребляемая из сети лампой и

дросселем мощность составляет Р_С = 50 [ Вт ]. Коэффициент мощности светильника Cos φ= 0,5, напряжение сети U = 220 [ В ]. Найти емкость конденсатора C для полной компенсации реактивной мощности в цепи лампы.
Задача № 2.

В параллель включено два потребителя, имеющих следующие электрические характеристики: Р₁ = 5 [ кВт ]; Сos φ₁= 0,5, Р₂ = 10 [ кВт ]; Cos φ₂= 0,6. U = 220 [ В ]. Найти емкость конденсатора C для полной компенсации реактивной мощности потребителей.

Задача № 3.

Электроприемник полной мощностью S = 10 [ кВА ] потребляет активную энергию Р = 5 [ кВт ]. Напряжение питающей сети составляет U = 220 [ В ]. В целях уменьшения реактивных потерь совместно с электроприемником (параллельно ему) включен фазосдвигающий конденсатор емкостью С = 500 [ мкФ ] ( рисунок 12.1).

Найти полную потребляемую мощность ( S_НК ) и коэффициент мощности (Соs φ _НК ) потребителя после неполной компенсации сдвига фаз.

.

R L C Рисунок 12.1  Электроприемник (RL) с фазосдвигающим конденсатором С

.

Задача № 4.

Электроприемник обладающий активным сопротивлением и индуктивностью ( последовательная RL цепь ) запитан от сети напряжением U = 220 [ В ], частотой f = 50 [ Гц ]. Ток протекающий через электроприемник I ₁ = 10 [ А ]; коэффициент мощности Соs φ ₁ = 0,68 (φ _НК = 46 ⁰ ). Для повышения коэффициента мощности параллельно RL цепи включили конденсатор С (рисунок 12.1). В результате ток, протекающий через RLC цепь снизился до величины I ₂ = 7,5 [А] , а коэффициент мощности стал равным: Соs φ₂ = 0,9 (φ_НК = 24,5). Найти емкость конденсатора, построить векторную диаграмму.
Задача № 5.

Электроприемник с активным сопротивлением и индуктивностью (последовательная RL цепь ) запитан от сети напряжением U = 220 [ В ], частотой f = 50 [ Гц ]. Ток протекающий через электроприемник составляет I ₁ = 10 [ А ]; коэффициент мощности Соs φ ₁ = 0,68 (φ _НК = 46 ⁰ ). Для полной компенсации угла сдвига фаз между векторами тока и напряжения в целях повышения коэффициента мощности параллельно RL цепи включили конденсатор С (рисунок 12.1). В результате коэффициент мощности увеличился и стал равным: Соs φ ₂ = 1 (φ _НК = 0 ⁰ ). Найти емкость конденсатора, построить векторную диаграмму, определить ток через RLC цепь.

Задача № 6.

Последовательно с реактором ( дросселем ) индуктивностью L = 0,1

[ Гн ] ( активное сопротивление которого составляет R _L = 10 [ Ом ] ) включено активное сопротивление R = 90 [ Ом ]. Для компенсации угла сдвига фаз между векторами тока и напряжения параллельно реактору включен конденсатор емкостью C = 40 [ мкФ ] (рисунок 12.2).

R L L R C Рисунок 12.2  Электроприемник (RL) с фазосдвигающим конденсатором С.

Определить коэффициент мощности цепи без компенсации и с компенсацией и реактивную мощность RLC цепи до и после компенсации, построить векторную диаграмму. Питающее напряжение цепи составляет 220 [ В ] частотой f = 50 [ Гц ].
Задача № 7

В цепь переменного тока напряжением U = 36 [ В ] параллельно включены RL и RC цепочки ( рисунок 12.3. ), значения сопротивлений которых составляют: R_L= 8 [ Ом ]; R _C = 3 [ Ом ]; X_L = 2 [ Ом ]; X_C = 10 [ Ом ]. Построить векторную диаграмму токов, найти полную и активную мощности RLRC цепи. Найти коэффициент мощности RL и RLRC цепей.

.

R1 L R2 C Рисунок 12.3  Электроприемник – параллельно включенные RL и RС цепочки

.
Задача № 8

. В цепь переменного тока напряжением U = 220 [ В ] параллельно включены RL и RC цепочки (рисунок 12.3), значения сопротивлений которых составляют: R_L = R_C = 12 [ Ом ]; | X_L| = | X_C | = 16 [ Ом ]. Построить векторную диаграмму токов, найти полную и активную мощности цепи. Найти коэффициент мощности RL и RLRC цепей.
Задача № 9

В цепь переменного тока частотой f = 50 [ Гц ] напряжением U = 36 [ В ] параллельно включены RL и RC цепочки (рисунок 12.3), значения сопротивлений которых составляют: R_L= 8 [ Ом ]; R _C = 3 [ Ом ]; X _L = 2 [ Ом ]. Найти емкость конденсатора при полной компенсации реактивной мощности (случай резонанса токов). Найти полную и активную мощности RLRC цепи. Найти коэффициент мощности RL и RLRC цепей.

Задача № 10

Последовательная RL цепь, включенная в сеть переменного тока напряжением U = 220 [ В ] (рисунок 12.4) потребляет активную мощность Р = 1,2 [ кВт ] . По цепи течет ток I = 11 [ А ]. Определить емкость конденсатора, который необходимо включить параллельно RL цепи, чтобы коэффициент мощности RLС цепи стол равным Соs φ = 0,91

R L C Рисунок 12.4  Электроприемник (RL) с фазосдвигающим конденсатором С

Задача № 11

Коэффициент мощности электроприемника с индуктивной составляющей состаляет Соs φ = 0,5 , напряжение сети U = 220 [ В ] , по цепи течет ток I = 60 [ А ]. Определить емкость конденсатора, включенного параллельно электроприемнику для повышения коэффициента мощности до величины Соs φ _К = 0,8. Найти суммарный ток цепи после компенсации реактивной мощности электроприемника и токи ветвей.

Задача № 12

Два активно – индуктивных электроприемника включенных параллельно в сеть напряжением U = 220 [ В ] мощностью Р ₁ = 5,5 [ кВт ] и Р ₂ = 2,92 [кВт] потребляют электрический ток I ₁ = 38,8 [ А ] и I ₂ = 22 [ А ] соответственно. Определить суммарный коэффициент мощности цепи. Рассчитать реактивную мощность, потребляемую конденсатором, который необходимо включить параллельно потребителю для частичной компенсации индуктивной мощности для повышения коэффициента мощности до Соs φ _К = 0,9. Найти суммарный ток, полную и реактивную мощности электропротребителя до и после частичной компенсации реактивной мощности.

12.2 Решение задач на компенсацию реактивной мощности
Задача № 1 . Решение.

1. 
   Находим тангенс угла потерь tg φ: _________
   

________ tg φ = ( Sin φ / Cos φ ) = [ (1 – Cos ² φ ) / (Cos φ ) ] =

= [ (1 – 0,5 ² ) / 0,5 ] = 1,73.

2. Из выражения 5.27 находим еакость фазосдвигающего конденсатора при полной компенсации сдвига фаз:

С = [ (РС tg φ ) / (ω  U 2 ) ] = [ (РС tg φ ) / ( 2 π  f  U 2 ) ] = = [ (50 1,73) / (2  3,14  50 2202 ) ] = 5,7  10 –6 [ Ф ].

Выбираем конденсатор стандартной емкости С = 6 [ мкФ ].

Задача № 2. Решение.

1. Находим тангенс угла потерь потребителей tg φ ₁ и tg φ ₂:

________

tg φ ₁ = ( Sin φ₁/ Cos φ₁) =[ (1 – Cos ²φ₁) / Cos φ₁ ) ] =

________

= [(1 – 0,5 ²) / 0,5 ] = 1,73.

__________

tg φ ₂ = ( Sin φ₂/ Cos φ₂ ) =[ (1 – Cos ²φ ₂) / Cos φ ₂ ) ] =

________

= [(1 – 0,6 ²) / 0,6 ] = 1,6.

2. 
   Из выражения 5.27 находим емкость фазосдвигающих конденсаторов при полной компенсации сдвига фаз потребителей:
   

С ₁ = [ (Р₁ tg φ₁) / (ω  U ² ) ] = [ (Р₁ tg φ₁) / ( 2 π  f U ² ) ] =

= [ (5000 1,73) / (2  3,14  50  220² ) ] = 569  10 ^–6 [ Ф ].

С 2 = [ (Р 2 tg φ 2) / (ω U 2 ) ] = [ (Р 2 tg φ 2) / ( 2 π  f U 2 ) ] = = [ (10000 1,6) / (2 3,14 50 2202 ) ] = 105 10 –6 [ Ф ].

3 . Суммарная емкость фазосдвигающих конденсаторов:

С _Σ = С ₁ + С ₂ = 569 + 105 = 674 мкФ

Задача № 3. Решение.

1. Находим коэффициент мощности потребителя RL без фазосдвигающего конденсатора С (рисунок 12.1 ): Cos φ = ( Р / S ) = (5 / 10 ) = 0,5

Q C φ Р Q L S Рисунок 12.5  Треугольник мощностей Р; Q ; S

2. Из выражения S = U  I [ ВАр ] находим полный ток I [ А ] в цепи некомпенсированного электропотребителя RL:

I = S / U = 10000 / 220 = 45,45 [ А ].

3. Из треугольника токов Cos φ = (I _АКТ / I ) находим активный ток I _АКТ:

I _АКТ = I  Cosφ = 45,45  0,5 = 22,725 [ А ].

4. Из треугольника токов находим реактивный (индуктивный) ток I _L:

_________ _______________ ___________

I _L = I ² - I _АКТ² =  I ² - (I ? Cosφ)² = I ²  1 - (Cosφ)² =

_________ __

= I ²  1 - (0,5)² = 0,5 I ²  3 = 0,5 45,45 1,73 = 39,3 [ А ].

5. Из треугольника мощностей находим реактивную (индуктивную) мощность Q _L: _______ ________

Q _L =  S ² - P ² =10² - 5² = 8,6 [ кВАр ].

6. Используя закон Джоуля – Ленца находим реактивное (индуктивное) сопротивление потребителя Х _L: Х _L= Q _L / (I _L) ² = 8600 / 3,93 ² = 5,6 [ Ом ].

7. 
   Используя закон Ома находим активное сопротивление потребителя R:
   

R = U / I _АКТ = 220 / 22,725 = 9,7 [ Ом ].

8. Найдем емкостное (реактивное) сопротивление Х_С фазосдвигающего конденсатора С (рисунок 12.1. ):

Х _С = 1 / ω С = 1 / 2 π f С = 1 / 2  3,14  50 0,0005 = 6,37 [ Ом ].

9. Определим полное сопротивление цепи Z [ Ом ] после шунтирования

ее фазосдвигающим конденсатором:

________ __________ |  R 2+ Х L2 | Х С |  9,72+ 5,6 2 |6,4 Z НК = – –––––––––––––––– = –––––––––––––––– = 7,4 [ Ом ].  R 2+ ( Х L - Х С ) 2 9,7 2+ ( 5,6 - 6,4 ) 2

10. Вычислим полную мощность электропотребителя S_НК [ ВА ] при неполной компенсации сдвига фаз: S_НК = U ² / Z _НК = 220² / 7,4 = 6540 [ ВА ]

11. Из треугольника мощностей вычислим коэффициент мощности электропотребителя Соs φ _НК при неполной компенсации сдвига фаз:

Соs φ _НК= P / S_НК = 5 / 6,54 = 0,76 .

Задача № 4. Решение.

1. 
   Найдем активный ток RL цепи ( рисунок 12.1 ):
   

I _А = I ₁  Соs φ ₁ = 10  0,68 = 6,8 [ А ].

0 I А U I2 Р I 2 I С I 1Р I 1 Рисунок 12.6  Векторная диаграмма активно – реактивного потребителя электрической энергии с фазосдвигающим конденсатором.

2. 
   Реактивный ток RL С цепи составит:
   

_____________ _______

I _{2 Р} = I ₂  Sin φ ₂ = I ₂ 1 - ( Соs φ ₂ ) ² = 7,5 1 - 0,9 ² = 3,3 [ А ].

4. Ток через конденсатор равен: I _С = I _1Р I _{2 Р} = 7,3 – 3.3. = 4 [ A ].

5. Реактивное сопротивление емкости определяется из соотношения:

Х _С = U / I _С = 220 /4 = 55 [ Ом ] .

6. 
   Тогда емкость конденсатора будет:
   

С = 1 / ω Х _С = 1 / 2 π  f Х _С = 1 / 2  3,14  50  55 =

= 0,0000579 [ Ф ].= 57,9 [ мкФ ]..

Выбираем ближайшиее номинальное значение С = 60 мкФ.

Задача № 5. Решение.

1. 
   Векторная диаграмма представлена на рисунке 12.7:
   

0 U I С φ1 I А = I RLC I1 I1Р Рисунок 12.7  Векторная диаграмма активно – реактивного потребителя электрической энергии с фазосдвигающим конденсатором при полной компенсации угла сдвига фаз между векторами тока и напряжения

Сначала откладываем вектор напряжения U. Под углом φ₁ к нему в масштабе откладываем вектор тока I ₁. Проведя пунктинрую нормаль к вектору напряжения U находим вектор активного тока I _А . Проведя параллельно вектору напряжения U пунктирную линию восстановим из начала координат нормаль до пересечения с этой пунктирной линией; в результате получим вектор реактивного ( индуктивного ) тока I _1Р , который отстает от вектора напряжения U на угол 90 ⁰ . При полной компенсации угла сдвига фаз между векторами тока и напряжения вектор реактивного ( емкостного ) тока I _С опережает вектор напряжения U на угол 90 ⁰ , и равен по пбсолюной величине вектору индуктивного тока I _1Р . Сдвинув вектор реактивного ( емкостного ) тока из начала координат параллельно самому себе в конец ( на острие стрелки вектора индуктивного тока I _1Р ) получаем векторную диаграмму при полной компкнсации угла сдвига фаз.

2. Найдем активный ток RL цепи:

I _А = I ₁  Соs φ ₁ = 10  0,68 = 6,8 [ А ].

3. Реактивный ток RL цепи составит:

_____________ ________

I _1Р = I ₁  Sin φ ₁ = I ₁1 - ( Соs φ ₁ ) ² = 10 1 - 0,68 ² = 7,3 [ А ].

4. Ток через конденсатор равен: I _С = I _1Р = 7,3 [ A ].

5. Определяем реактивное сопротивление емкости:

Х _С = U / I _С = 220 /7,3 = 30,137 [ Ом ] .

6. 
   Тогда емкость конденсатора будет:
   

С = 1 / ω Х _С = 1 / 2 π  f  Х _С = 1 / 2  3,14  50  30,137 =

= 0,000096 [ Ф ].= 96 [ мкФ ]..

. 7. В этом случае ток через RLC цепи будет равен активному току :

I _RLC = I _А = 6,8 [ А ]

и наблюдается резонанс токов

.

Задача № 6. Решение.

1. 
   Найдем реактивное сопротивление индуктивности ( реактора ) и емкости ( конденсатора ) :
   

Х _L = ωL = 2 π  f  L = 2  3,14  50  0,1 = 31,4 [ Ом ];

Х _С = 1 / ω  С = 1 / 2 π  f  C = 1 / 2  3,14  50  0,00004 = 79,6 [ Ом ].

2. Определим полное сопротивление цепи до компенсации:

_______________ _________________

Z ₁ =  ( R_L + R ) ² + Х _L ² =  ( 10 + 90 ) ² + 31,4 ² = 104,8 [ Ом ].

3. Вычислим полный ток RL цепи до компенсации ( Рис. 6.):

I ₁ = U / Z ₁= 220 / 104,8 = 2,1 [ А ].

4. Реактивная Q ₁, активная Р ₁ и полная мощности S ₁ RL цепи до компенсации равны:

Q ₁ = Х_L I ₁ ² = 31,4  2,1 ² = 138,5 [ ВАр ] ;

Р ₁ = ( R_L + R )  I ₁ ² = ( 10 + 90 )  2,1 ² = 441 [ Вт ] ;

S ₁ = Z ₁ I ₁ ² = 104,8  2,1 ² = 462,2 [ ВА ] .

5. Коэффициент мощности RL цепи до компенсации составляет:

Соs φ ₁ = Р ₁ / S ₁= 441 / 462,2 = 0,95 .

6. Активный и реактивный токи RL цепи до компенсации определяются из соотношений : I _1А = I ₁  Соs φ ₁ = 2,1  0,95 = 2 [ А ];

_____________ _________

I _1Р = I ₁  Sin φ ₁ = I ₁1 - ( Соs φ ₁ ) ² = 2,1  1 - 0,95 ² = 0,7 [ А ].

7. Векторная диаграмма RL цепи до компенсации  рисунок 5.10.

8. Определим полное сопротивление реактора до компенсации:

__________ __________

Z _Р =  R_L ² + Х _L ² =  10 ² + 31,4 ² = 32,95 [ Ом ].

В комплексной форме:. __

Z _Р = R_L + j Х _L = 10 + j 31,4 [ Ом ].

0 φ1 I A1 U I P1 I 1 Рисунок 12.8. Векторная диаграмма RL цепи до компенсации.

9. Полное сопротивление в комплексной форме записи фазосдвигающего конденсатора и реактора после компенсации определяются выражениями: __

Z _С = – j Х _С = – j 79,6 [ Ом ].

___ ___ __ __ __

Z _РК = (Z _Р  Z _С ) / (Z _Р + Z _С ) = (10 + j 31,4) (– j 79,6 ) / (10 + j 31,4 – j 79,6)=

= (2499 – j 796) / ( 10 – j 48,2) = (2499 – j 796) (10 + j 48,2) / (10 ² + 48,2 ²) =

= (24990 + 38367 + j 120452 – j 7960 ) / ( 100 + 2323) =

= ( 63357 + j 112492) / 2423 = 26,15 + j 46,43 [ Cм ].

Или: ___________ ______________

Z _РК =  R _РК ² + X _РК ² =  26,15 ² + 46,43 ² = 53,3 [ Cм ]

10. Найдем полное сопротивление цепи после компенсации:

__ __ __

Z _К = Z _РК + Z _R = 26,15 + j 46,43 + 90 = 116,15 + j 46,43 [ Ом ].

Или: __________ ______________

Z _К =  R _К ² + X _К ² =  116,15² + 46,43 ² = 125,1 [ Cм ]

11 . Реактивное сопротивление цепи после компенсации составило:

Х _К = 46,43 [ Ом ].

Так как реактивное сопротивление цепи увеличилось, следует говорить о недокомпенсации.

12. Активное сопротивление цепи:

R _A = 116,15 [ Ом ].

13. Вычислим полный ток RLС цепи ( Рис. 6.):

I _К = U / Z _К = 220 / 125,1 = 1,76 [ А ].

14 . Реактивная Q _К, активная Р _К и полная мощности S _К RLС цепи после компенсации равны:

Q _К = Х _К? I _К ² = 46,43 ? 1,76 ² = 143,8 [ ВАр ] ;

Р _К = R_А  I _К ² = 116,13  1,76 ² = 359,7 [ Вт ] ;

S _К = Z _К I _К ² = 125,1  1,76 ² = 387,5 [ ВА ] .

15. Коэффициент мощности RLС цепи после перекомпенсации:

Соs φ _К = Р _К / S _К= 359,7 / 387,5 = 0,93 .

16. Активный и реактивный токи RLС цепи после перекомпенсации определяются из соотношений : I _АК = I _К  Соs φ _К = 1,76  0,93 = 1,64 [ А ];

_____________ _________

I _ХК = I _К  Sin φ _К = I _К1 - ( Соs φ _К ) ² = 1,76  1 - 0,93 ² = 0,65 [ А ].

17 . Векторная диаграмма RLС цепи после перекомпенсации:

0φК I AК U I ХК I К Рисунок 12.10  Векторная диаграмма RLС цепи после компенсации.

Задача № 7. Решение.

1. Нпйдем полное сопротивление RL и RC цепей::

_________ _________

Z _RL = R _L ² +X_L ² = 12 ² + 16 ² = 20 [ Oм ];

_________ _________

Z _RC = R _C ² +X_C ² =  12 ² + 16 ² = 20 [ Oм ].