лабы архитект. Методические указания к лабораторным работам для студентов 1го курса фпми
 Скачать 417 Kb. Скачать 417 Kb.
|
|
Операции преобразования типов
Другие функции
Команды для инициализации и работы с памятью Инициализация памяти
Инициализация значений
Операции записи
Поддержка кэш-памяти в SSE
3. Использование встроенных функций SSE в программе на языке Си // скалярное произведение векторов #include #include #define N 10000000 // «обычная» функция float inner1(float *x,float *y,int n) { float s; int i; s=0; for(i=0;i s+=x[i]*y[i]; return s; } // функция с использованием SSE intrinsics float inner2(float *x,float *y,int n) { float sum; int i; __m128 *xx,*yy; __m128 p,s; xx=(__m128 *)x; yy=(__m128 *)y; s=_mm_set_ps1(0); for (i=0;i { p=_mm_mul_ps(xx[i], yy[i]); // векторное умножение четырех чисел s=_mm_add_ps(s,p); // векторное сложение четырех чисел } p=_mm_movehl_ps(p,s); // перемещение двух старших значений s в младшие p s=_mm_add_ps(s,p); // векторное сложение p=_mm_shuffle_ps(s,s,1);//перемещение второго значения в s в младшую позицию в p s=_mm_add_ss(s,p); // скалярное сложение _mm_store_ss(&sum,s); // запись младшего значения в память return sum; } int main() { float *x,*y, s; long t; int i; // выделение памяти с выравниванием x=(float *)_mm_malloc(N*sizeof(float),16); y=(float *)_mm_malloc(N*sizeof(float),16); for (i=0;i { x[i]=10*i/N; y[i]=10*(N-i-1)/N; } // Using x87 s=inner1(x,y,N); printf("Result: %f\n",s); // Using SSE s=inner2(x,y,N); printf("Result: %f\n",s); _mm_free(x); _mm_free(y); return 0; } Задание. Реализовать процедуру умножения квадратных матриц (размером кратным четырём) без использования специальных расширений и с использованием расширений SSE, сравнить время выполнения этих реализаций (Обязательное задание – 10 баллов). В соответствии с вариантом задания реализовать матрично-векторную (с одинаковым размером матриц и векторов кратным четырём) процедуру с использованием расширений SSE (Дополнительное задание – 7 баллов). С использованием инструкции cpuid определить наличие расширения SSE (Дополнительное задание – 3 балла). Крайний срок сдачи – 7 мая 2011 года. Варианты. В предложенных вариантах предполагается, что Операция Операция Операция Операция Операция Операция Операция Операция Операция Операция Лабораторная работа № 4 Программирование многоядерных архитектур Цель работы. Использование интерфейса OpenMP для программирования простых многопоточных приложений. Методические указания. 1. Интерфейс OpenMP OpenMP – интерфейс прикладного программирования (API) для масштабируемых SMP-систем (симметричные мультипроцессорные системы) в модели общей памяти. Исполняемый процесс в памяти может состоять из множественных нитей, которые имеют общее адресное пространство, но разные потоки команд и раздельные стэки. В простейшем случае, процесс состоит из одной нити, выполняющую функцию main. Нити иногда называют также потоками, легковесными процессами, LWP (light-weight processes). OpenMP основан на существовании множественных потоков в общедоступной памяти [3]. Схема процесса представлена на рисунке. 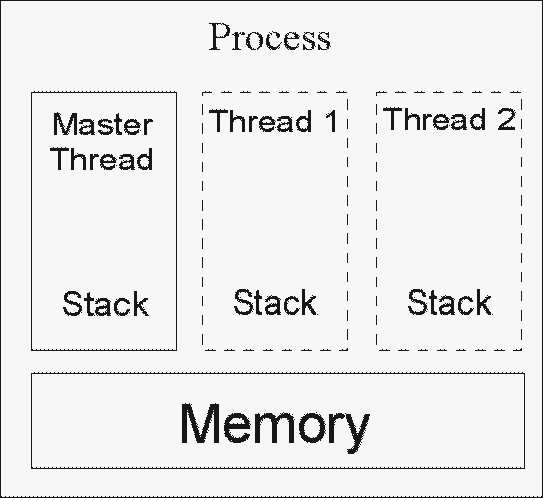 Рисунок 8. Все программы OpenMP начинаются как единственный процесс с главным потоком. Главный поток выполняется последовательно, пока не сталкиваются с первой областью параллельной конструкции. Создание нескольких потоков (FORK) и объединение (JOIN) проиллюстрировано на рисунке. 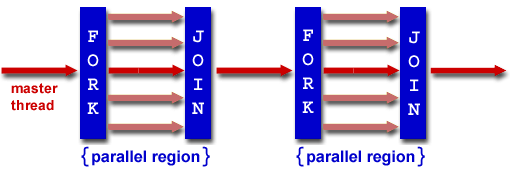 Рисунок 9. 2. Примеры программ с использованием OpenMP 2.1. Определение и печать номера потока #include #include void main () { int nthreads, tid; /* Fork a team of threads giving them their own copies of variables */ #pragma omp parallel private(tid) { /* Obtain and print thread id */ tid = omp_get_thread_num(); printf("Hello World from thread = %d\n", tid); /* Only master thread does this */ if (tid == 0) { nthreads = omp_get_num_threads(); printf("Number of threads = %d\n", nthreads); } } /* All threads join master thread and terminate */ } 2.2. Распределение работы #include #include #define CHUNKSIZE 100 #define N 1000 void main () { int i, chunk; float a[N], b[N], c[N]; /* Some initializations */ for (i=0; i < N; i++) a[i] = b[i] = i * 1.0; chunk = CHUNKSIZE; #pragma omp parallel shared(a,b,c,chunk) private(i) { #pragma omp for schedule(dynamic,chunk) nowait for (i=0; i < N; i++) c[i] = a[i] + b[i]; } /* end of parallel section */ } 2.3. Использование секций #include #include #define N 1000 void main () { int i; float a[N], b[N], c[N], d[N]; /* Some initializations */ for (i=0; i < N; i++) { a[i] = i * 1.5; b[i] = i + 22.35; } #pragma omp parallel shared(a,b,c,d) private(i) { #pragma omp sections nowait { #pragma omp section for (i=0; i < N; i++) c[i] = a[i] + b[i]; #pragma omp section for (i=0; i < N; i++) d[i] = a[i] * b[i]; } /* end of sections */ } /* end of parallel section */ } 2.4. Параллельная реализация одиночных циклов #include #include #define N 1000 #define CHUNKSIZE 100 void main () { int i, chunk; float a[N], b[N], c[N]; /* Some initializations */ for (i=0; i < N; i++) a[i] = b[i] = i * 1.0; chunk = CHUNKSIZE; #pragma omp parallel for shared(a,b,c,chunk) private(i) schedule(static,chunk) for (i=0; i < n; i++) c[i] = a[i] + b[i]; } 2.5. Критические секции #include void main() { int x; x = 0; #pragma omp parallel shared(x) { #pragma omp critical x = x + 1; } /* end of parallel section */ } 2.6. Редуцируемые операции #include #include void main () { int i, n, chunk; float a[100], b[100], result; /* Some initializations */ n = 100; chunk = 10; result = 0.0; for (i=0; i < n; i++) { a[i] = i * 1.0; b[i] = i * 2.0; } #pragma omp parallel for default(shared) private(i) schedule(static,chunk) \ reduction(+:result) for (i=0; i < n; i++) result = result + (a[i] * b[i]); printf("Final result= %f\n",result); } Задание. В соответствии с вариантом задания реализовать алгоритм с использованием интерфейса OpenMP (Дополнительное задание: варианты 1,2 и 3 – 20 баллов, вариант 4 – 30 баллов). Защита лабораторной работы (Дополнительное задание – 10 баллов). Крайний срок сдачи – 20 мая 2011 года. Крайний срок защиты – 25 мая 2011 года. Варианты. Скалярное произведение двух векторов. Умножение матрицы на вектор. Умножение матрицы на матрицу. Решение системы линейных алгебраических уравнений методом Гаусса. Литература Спецификация инструкции cpuid для процессоров Intel http://www.intel.com/Assets/PDF/appnote/241618.pdf Спецификация инструкции cpuid для процессоров AMD http://support.amd.com/us/Embedded_TechDocs/25481.pdf Корнеев В.Д. Параллельное программирование кластеров // Новосибирск. НГТУ. 2008. – 312 с. |
