Лабы. ЛабРаб_С_Шафеева. Методические указания к лабораторным работам Омск 2008 Составители Ольга Павловна Шафеева, канд техн наук, доцент
 Скачать 0.93 Mb.
|
Задание 1 (программа 1_1)
Задание 2 (программа 1_2) Идет k секунда суток. Определить, сколько целых часов (h) и целых минут (m) и секунд (s) прошло к этому моменту. Определить площадь трапеции с основаниями а, b, высотой h и объем усеченного конуса, если считать а, b - площадями оснований. 3. Определить координаты центра тяжести трех материальных точек с массами m1,m2,m3 и координатами (x1,y1), (x2,y2), (x3,y3). 4. Вычислить по заданному радиусу R объем шара и площадь круга, найти соотношение между ними. 5. Вычислить медианы треугольника по заданным сторонам a, b, c. 6. Вычислить площадь поверхности и объем конуса по заданным радиусам и высоте h. 7. По заданному радиусу найти объем шара и площадь поверхности. 8. Вычислить, какая идет секунда суток при положении стрелок в h часов, m минут и s секунд, а также угол (в градусах) между положением часовой стрелки в начале суток и ее положением в указанный момент. 9. Ввести двузначное целое число х<15. Написать программу перевода его в восьмеричную систему счисления. 10. Ввести координаты двух точек (х1, y1), (x2,y2). Найти расстояние между ними. Лабораторная работа 2 Программирование разветвленных алгоритмов. Операторы передачи управления Структура условного оператора передачи управления: if (<выражение>) <оператор 1> else <оператор 2>; (Если) (иначе) - ключевые слова, где <условие> - это произвольное выражение логического типа, которое может принимать два значения: истина (TRUE) и ложь (FALSE); <оператор> - любой оператор языка СИ, заканчивается точкой с запятой. Сокращенная форма условного оператора: if (<выражение>) <оператор>; Оператор безусловного перехода: goto <идентификатор-метка>; Меткой является идентификатор. Метка размещается перед оператором С/С++, к которому выполняется переход и отделяется двоеточием (:). Пример 1. Составить программу для начисления базовой зарплаты согласно следующему правилу: если стаж работы сотрудника менее трех лет, то зарплата равна 100$, при стаже работы от трех до 5 лет - 150$, свыше 5 лет зарплата повышается с каждым годом на 10$, причем при стаже, превышающем 20 лет, она составляет 300$. Для программирования решения этой задачи определим математическую формулировку задачи:  100, если ST < 3;ZP= 150, если 3 ≤ST 5; 150+ (ST -5)*10, если 5 < ST≤ 20; 300, если ST > 20; где ZP - зарплата, ST - стаж работы. Далее построим СА (рис.2,а), ей соответствует следующая программа: #include #include void main () { int ST; // ST - стаж (байтовый (целый) тип беззнаковый) float ZP; // ZP - зарплата (плавающий тип) printf ("\n Введите стаж "); scanf ("%d",&ST); if (ST<3) ZP = 100; else if (ST<5) ZP = 150; else if (ST>=20) ZP=300; else ZP=150+(ST- 5)*10; printf ("\n Зарплата = %10.2f$\n",ZP); getch(); } Оператор выбора switch позволяет в зависимости от значения какой-либо переменной или выражения (ключа выбора) выполнить те или иные операторы, помеченные соответствующими константами. Структура оператора: switch (<выражение> ) { case <константа 1>: <группа операторов 1>; case <константа 2>: <группа операторов 2>; . . . case <константа N>: <группа операторов N> default: <операторы>; 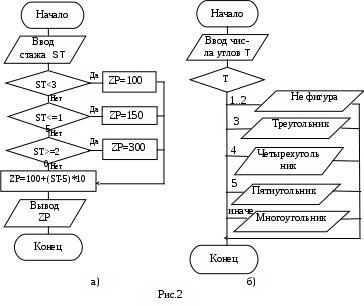 } где <выражение> - выражение (переменная) любого порядкового типа; <константа> - константа того же типа, что и <выражение>; <оператор> - произвольный оператор C/C++. Пример 2.Напечатать в зависимости от числа углов название фигуры (треугольник, четырехугольник, пятиугольник, шестиугольник, многоугольник). Вариант реализации задачи с применением оператора выбора представлен СА (рис.2,б) и следующей программой: #include #include void main () { int T; // T – число углов clrscr(); // очистка экрана printf ("Введите число углов "); scanf ("%d",&T); switch (T) { case 1: case 2 : printf ("Это не фигура\n "); break; case 3: printf ("С %d углами - треугольник\n ", T); break; case 4: printf ("С %d углами - четырехугольник\n ", T); break; case 5 : printf ("С %d углами - пятиугольник\n ", T ); break; case 6: printf ("С %d углами - шестиугольник\n ", T ); break; default : printf ("С %d углами - многоугольник\n ", T ); } getch(); } Задание 1 (программа 2_1) Вычислить значение функции в зависимости от интервала, в который попадает вводимый с клавиатуры аргумент: 1  . Для t [0,3],  a t2 ln t при 1 ,где a=-0.5,b=2 z = 1 при t<1, e a t cos b t при t>2, 2  . Для x [0,4],  при x2,где а=2.3 f = х при 0.3< x 2, cos(x-a) при x  ,3 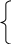 . Для x [0,7], (a+b)/(ex+cosx) при 0 x2.3,где a=-2.7,b=-0.27 z = (a+b)/(x+1) при 2.3 x5, ex+sinx при 7  ,4 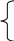. Для i [7,12], a i4 + b i при i< 10, где a=2.2,b=0.3. y = tg(i + 0.5) при i = 10, e2i +  при i >10,5  . Для x [0.9,5],  x2 - 7/x2 при x<1.3,где a=1.5 y = ax3 + 7  при 1.3 x3,lg(x + 7 ) при x , 6  . Для t [-1.4],  при t<0.1,где a=2.1,b=0.37. z = at + b при 0.1 t 2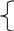,  при t ,7  . Для x [0,6], a esin x +2.5 при x<0.3,где a=1.5. y = ecos x + a при 0.3 x<4,  (sin x)/ (a + ex) при x 4,8. Для x [1,2], y = a/x + b x2 - c при x ,где a=1.8,b=-0.5, c=3.5 (a + bx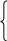)/  при x>1.2, 9  . Для t [1,5], t при t>a,где a=2.5 z = t sin a t при t=a, e-at cos a t при t  10. Для x [0,4], e-bx sin b x при x<2.3,где a=1,b=3. y= сos bx при 2.3  ,e-ax cos b x при x  1 1. Для t [0.5,3], a t2 – b  при tгде a=1.3,b=6.5 z= a - b при a  a t2/3 -  при t>b, 12. Для x [0,2], |e-2x sin bx| при x >1,где b=-2.9 y = cos bx при x = 1, e-x cos bx при x < 1,  13. Для x [0.5,2] sin (cos a x) при x >1,где a=-0.8 z = tg ax при x = 1, a2 x при x < 1, 1  4. Для x [1,2], ln bx - 1/(bx+1) при x < 1.3,где b=1.3. y = bx + 1 при 1.3 x 1.7, ln bx +1/(bx+1) при x > 1.7, 15. Для x [-1,1], ax2+bx2/3 при x<0.1, где a=2.5,b=-0.9. z= a x2 при x=0.1, b x2/3 при x>0.1. 16. Ввести координаты точки (x, y). Напечатать, в каком квадранте или на какой оси координат находится эта точка. 17. Ввести радиусы R1, R2 и высоту. Вычислить объем усеченного конуса:  , где S- площадь оснований. Если R1 = R2 - объем и площадь цилиндра, если R1 = 0 или R2 = 0 - объем (hπr2) и площадь πr( ) поверхности конуса.18. Ввести с клавиатуры цифру. Определить, какой системе счисления она может принадлежать. 19. Ввести число. Определить, делится ли оно нацело на два, три или пять. 20. Ввести a, b, h. Если h=0, вычислить площадь прямоугольника; при a = b, найти площадь квадрата; в противном случае подсчитать площадь трапеции. Задание 2 (программа 2_2) 1. Определить остаток от деления на восемь введенного числа х и написать восьмиричную цифру прописью. 2. По цифре, введенной с клавиатуры, напечатать название этой цифры. 3. С клавиатуры ввести число k (1..30). Определить, какому дню недели оно соответствует, если первое число - понедельник. 4. Ввести число и номер месяца. Напечатать дату прописью. 5. Идет k секунда суток. Вычислить, сколько прошло часов и полных минут к этому моменту, при этом согласовать со значением слова (час, часа, часов, минута, минуты, минут). 6. В зависимости от номера (N) типа фигуры, организовать ввод необходимых данных и вычислить при N = 1 - площадь круга, N = 2 - объем шара (4/3πR3), N=3 -объем цилиндра, N = 4 - площадь поверхности сферы 4πr2. 7. Ввести число N (0 ≤ N ≤ 15). Определить и напечатать шестнадцатеричную цифру, ему соответствующую. 8. Для целого числа К (1…99) напечатать фразу « Мне К лет », при определенных значениях К слово «лет» заменить словом «год» или «года». 9. В зависимости от номера (N) типа фигуры, организовать ввод необходимых данных и вычислить при N = 1 - площадь прямоугольника, при N=2 - площадь параллелограмма, при N = 3 - площадь трапеции 1/2(a+b)h. В последнем случае напечатать: является ли трапеция параллелограммом или ромбом. 10. Перевести число 0 ≤ х ≤ 31 в шестнадцатеричную систему счисления. 11. Напечатать прописью остаток от деления любого целого числа на пять. 12. По введенному номеру напечатать нужный цвет в радуге. 13. Спроектируйте программу, которая показывает, что, если сумма цифр двузначного числа кратна трем, то и само число делится на три без остатка. 14. Разработайте программу, которая доказывает, что квадрат двузначного числа k5 (последняя цифра - 5), равен k * (k + 1) * 100 + 25 (т.е. может быть получен умножением старшей цифры k на следующую по порядку и припиской «25»). Например, 35 * 11 = 3*4*100 + 25. Для задания 2 номер варианта определяется остатком от деления индивидуалного варианта на число 12. Лабораторная работа 3 Программирование циклических алгоритмов с заданным числом повторений Оператор цикла с счетчиком: for (<выражение1> ; <условие выполнения> ; <выражение2>) <оператор>; где <выражение1> - это выражение инициализации цикла (может содержать несколько операторов, разделенных запятыми); <выражение2> - изменение параметра цикла (не обязательно целое). Пример 1. Вычислить сумму элементов s=1+1/4+1/9+1/16+... . На основе анализа изменения параметра знаменателя определим алгоритм решения задачи (pис. 3) и напишем программу: #include # 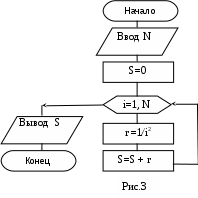 include void main () { float s = 0, r; int i,N; clrscr(); //очистка экрана printf ("\n Введите N "); scanf ("%d",&N); for ( i=1; i<=N; i++ ) { r = 1.0/ (i*i); s+ = r; // s = s + r } printf ("Сумма = %6.2f\n ",s); getch(); } Пример 2. Вычислить значения двух функций F1(x) = tg(x) и F2(x) = sin(x) в n точках, равномерно распределенных на интервале a ≤ x ≤ b, где a = -π/4, b = π. Для реализации первого варианта данной задачи разработана СА (pис. 4) и cледующая программа: # 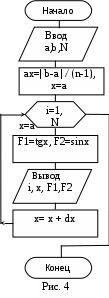 include #include #include # define b 3.1415 void main () { float F1, F2, x, dx, a = - b/4; // dx - шаг изменения x int i, n; // i - переменная цикла clrscr(); // очистка экрана printf ("Введите число точек \n"); scanf ("%d", & n); dx = fabs(b-a)/(n-1); x = a; printf (" ___________________ \n"); printf ("| I | X | F1 | F2 | \n"); printf ("|---|--------|--------|--------|\n"); for ( i=1; i<=n; ++i ) // оператор цикла { F2 = sin(x); F1 = tan(x); // вычисление tg x printf (" |%3d| %8.3f |%8.4f| %8.4f|\n", i, x, F1, F2); x=x+dx; // x += dx } printf (" ____________________ \n"); getch(); } Если точки не нумеровать, можно в цикле применить параметр х и шаг изменения dx. Тогда во втором варианте программы оператор цикла имеет вид: for ( x = a; x <= b + dx/2; x+ = dx ) { . . . } Задание 1 (программа 3_1) Для заданных с клавиатуры значений переменных x и n вычислить 1. X = 1 + 1/2 + 1/3 + ... + 1/10. 2. Z = 2. 4. 6. 8. ... .20. 3. Y = -x + 4x - 9x + ... - 81 x.. 4. Y = x + x/3 + x/5 + ... + x/17. 5. Y = n! = 1. 2 . 3 .....n. 6. Y = 1 - 3 + 32 - 33 + . . . + 310. 7. Y=  x2/(2i-1). 8. Z =  (x+i)/i. 9. Y= x2/i. 10. Y = 1 + x/2 + x2/4 + x3/6 + ... + xi/2i + ... + x9 /18 . 11. Y = 1 + x2/1! + x4/2! + x6/3! + … + x20/10! = 1 +  x2i/i!. 12. Y = 1 - x +x3/3! -x5/5!+ ...+(-1)n x2n-1/(2n-1)!+ ... +x11/11!. 13. е = 1 + 1/1! + 1/2! + ... + 1/n! + ... (сравнить результат со значением функции EXP(1), определенной в Паскале). 14. π = 4(1-1/3+1/5-1/7+…+(-1)n/(2n+1)+…) (результаты сравнить с определенным в языке Паскаль числом Pi). 15. Y = arctg x = x - x3/3 + x5/5- ... + (-1)n x2n+1/(2n+1)+ ... (|х|<1). 16. Z = LN(1+x) = x - x2/2 + x3/3 - ... + (-1)n-1 xn/n + ... (|x|<1). 17. S = x - x3/3! + x5/5! - ... +(-1)n x2n+1/(2n+1)! + ... . 18. Вычислить суммы положительных и отрицательных значений функции z = cos(nx + a) sin(nx-a), где n = 1,2,...,5, a и x - вещественные числа. 19. Вычислить сумму четных и сумму нечетных чисел натурального ряда до N. 20. Найти сумму факториала M=  i !.Задание 2 (программа 3_2, программа 3_3) Вычислить значения двух функций в n равномерно распределенных в диапазоне а≤x≤b точках. Результаты оформить в виде таблицы.
Программирование циклических алгоритмов с предусловием Цель работы: научиться разрабатывать и отлаживать программы с неразветвленными и разветвленными циклами, управляемыми условиями. Структура оператора цикла с предусловием (с предварительной проверкой условия): while ( <выражение>) <оператор>; где <выражение> - это любое логическое выражение, <оператор> - это произвольный оператор Си, в том числе и составной. Пример. Для трех значений а = 0.1, 0.2, 0.3 протабулировать функцию y=a.tg(x/4) при изменении аргумента x на интервале [0.5,0.9] с шагом, равным a. Д 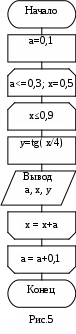 ля СА (рис.5) решения данной задачи программа может быть следующей:#include #include #include void main () { float a,x,y; clrscr(); printf ("-------------------------------\n"); printf (" a| x| y |\n"); printf ("-------------------------------\n"); a=0.1; while (a<=0.31) { printf ("%5.2f\n",a); x = 0.5; while (x<=0.91) { y=a*tan(x/4); printf (" %12.2f| %10.2f\n",x,y); x=x+a; // x+=a; } printf("-------------------------------\n"); a=a+0.1; // a+=0.1; } getch(); } Второй вариант программы можно реализовать через циклы …. Задание 1 (программа 4_1) Начертите структурную схему алгоритма, напишите и отладьте программу для табуляции следующих функций: 1. S = a e-xsin ax+  при -1 <= x <=1 с шагом 0.2,a = 0.75, 1<=y <=5 с шагом 1.5. 2. Z =  + 1,3 sin(x-a) при 2 <=x <=5 с шагом 0.5,a = 1.9, -1<=y<=1 с шагом 0.5. 3. S = e2 t ycos(t-a) при 1<=t<=2 с шагом 0.2,a = -2.1, 2<= y<=3 с шагом 0.3. 4. Z = bx  (tx+2.1) при 1<= x<=2 с шагом 0.2, b = 3.5 0<= t<=1 с шагом 0.2.   , если 0 <= x <= 2, a = 0.50; 0.75, Z= если 2 < x <= 3.6, шаг dx=a/2. 6   . sin ax - , если 0.1 <=x <= 0.4,Y= a cos2(px), если 0.4 < x <= 1.2, a = 1.0; 1.5,  2 - sin ax, если 1.2 < x <=1.6, шаг dx=a/5.7 . Z= ln(a+x2/ ) , если 0 <=x <= 2, a=1.0; 1.3; 1.6,2 e2x , если 2 < x <= 3.6, шаг dx=a/4. 8  . a(ex+2a+e-(x-3a), если 0.1 <= x < 0.5, Z = sin x, если x = 0.5, a = 2; 2.1, a + a cos(x+3a), если 0.5 < x <= 1.5, шаг dx=a/10. 9 . -a ex-3a, если 0 < x<= 3, a = 1; 1.5,Z= -a(1+ln(x-3a)), если 3 < x <= 4, шаг dx=a/2. 1 0. - (x+3a)2 - 2a, если -1 <=x <= 0, a = 0.7; 1,Y = a cos(x+3a) - 3a, если 0 < x < 1, dx=(a+0.2)/2.  a ex, если x = 1, 1 1. a(x-a)3/2, если 1 <= x <= 2.5, a = 0.5; 1.0,Z= a/2(ex/a+e-x/a), если 2.5 < x <= 4, шаг dx=a/2. 1 2.  , если 0.5 <= x < 1.5, a=0.1; 0.2; 0.3,Y = a cos x, если x = 1.5, шаг dx=2a. (a x2 + 1)x, если 1.5 < x <= 3, 1 3. (sin2x +a)2 ea sinX , если 0.1<=x<= 0.5, a=0.1;0.2;0.3,Z = tg(x/4), если 0.5 < x <=0.9, шаг dx=a. 1  4. tg(a2 +sin px), если 0 <= x <= 1, Y = a sin(p- cos px), если 1 < x <= 2, a=0.5; 0.75; 1; lg x, если 2 < x < 3, шаг dx=a/4. 1 5. Z= ecos x -a sin2(px), если 0.5 <= x <= 1.5 a=0.1;0.7;1.3,a x2 - cos px, если 1.5 < x <= 2 шаг dx= a/4. 1 6. 1/x, если 0.1 <= x <= 0.4 Y = ln(x2+ ax), если 0.4 < x <= 1.2 a = 1.0; 1.5, x2, если 1.2 < x < 1.6 шаг dx = a/5. 17. Дана непустая последовательность различных натуральных чисел, за которой следует нуль (признак конца последовательности). Определить порядковый номер наименьшего из них и его значение. 18. Найти первый отрицательный член последовательности cos (ctg), где n = 1,2,3,... . Напечатать его номер и значение. Распечатать всю последовательность 19. Вычислить наибольший общий делитель (k) натуральных чисел d и f. Оператор FOR не использовать. 20. Дан ряд неотрицательных вещественных чисел. Определить, сколько из них больше своих «соседей»: предыдущего и последующего чисел. Признаком окончания ряда чисел считать появление отрицательного числа. Задание 2 (программа 4_3) Модифицировать (изменить) программу 3_2 для вычисления функций F1(x) и F2(x) с применением вместо счетного цикла оператора цикла с предусловием. Выполнить ее и сравнить результаты с полученными в предыдущей работе. Лабораторная работа 5 Программирование циклических алгоритмов с постусловием Стpуктуpа оператора цикла с постусловием do {<операторы>} while (<условие выполнения>); Пример. Вычислить 15 значений функций y1(x) = tg(x); и y2(x) = ctg(x) при a ≤ x ≤ b, a=0.6*Pi, b=0.7*Pi. Для вычислений разработана СА (рис.6) и следующая программа: #include #include #include void main() {  int n=14; float a=0.6*M_PI, b=0.7*M_PI; float x, y1, y2, dx; clrscr(); dx=fabs((a-b)/n); x=a; do { y1=tan(x); y2=1/y1; printf ("x= %6.4f y1= %7.4f y2= %7.4f\n",x,y1,y2); x=x+dx; } while (x<=b); getch(); } Пример 2. Вычислить сумму элементов s = 1+1/4+1/9+1/16+... c точностью до E = 0.00001 (рис. 7). #include #include void main () { 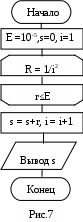 float E=0.00001; float s, r; // s- сумма, r-слагаемое int i; // счетчик слагаемых s = 0; i = 1; do { r = 1.0/(i*i); // вычисление слагаемых s = s + r; // s+ = r; i++ ; // i = I +1; } while (r>E); // сравнение слагаемых с Е printf ("Сумма=%9.5f\n",s); // вывод суммы getch(); } Задание 1 (программа 5_1) |
- sin x
e -x