Главная страница
Навигация по странице:

  • Задание 3

  • Программирование алгоритмов обработки одномерных массивов

  • [конст. выраж1][конст. выраж2]…;

  • Обработка двумерных массивов

  • [конст. выраж1][конст. выраж2]…, [конст. выраж1][конст. выраж2]…;

  • Задание

  • Задание 2

  • Программирование с применением функций

  • [класс] тип имя ([список параметров])[

  • Программирование с возвратом из функций нескольких значений

    		•

    Лабы. ЛабРаб_С_Шафеева. Методические указания к лабораторным работам Омск 2008 Составители Ольга Павловна Шафеева, канд техн наук, доцент


    Скачать 0.93 Mb.
    НазваниеМетодические указания к лабораторным работам Омск 2008 Составители Ольга Павловна Шафеева, канд техн наук, доцент
    Дата17.12.2020
    Размер0.93 Mb.
    Формат файлаdoc
    Имя файлаЛабРаб_С_Шафеева.doc
    ТипМетодические указания
    #161701
    страница4 из 8
    1   2   3   4   5   6   7   8
    Модифицировать программу 3_2 для вычис­ления функций F1(x) и F2 (x) с применением опе­ратора цикла с постусловием. Выполнить ее и сравнить результаты с полученными ранее.

    Задание 2 (программа 5_2)

    Начертить структурную схему алгоритма, написать и отладить прог­рамму для одной из следующих задач.

    1. Вычислить приближенное значение z = arctg x и сравнить с

    x - x3/3 + x5/5 - ... + (-1)nx2n+1/(2n+1) + ... (|х|<1), прекращая вычисления, когда очередной член по абсолютной величине бу­дет меньше eps=0.00001.

    2. Вычислить y = x - x2/2 + x3/3 - ... + (-1)n-1xn/n + ... с точностью eps=0.00001, где |x|<1. Сравнить результат с вычисленным через стандартную функцию значением y = LN(1+x).

    3. Вычислить y = 1 + x/1! + x2/2! + ... + xn/n! + ... с точностью eps=0.00001 и срав-нить результат с вычисленным через стандартную функцию значением y = ЕXP(x).

    4. Вычислить y = sin x = x - x3/3! +x5/5! -...+ (-1)nx2n+1/(2n+1)!+... с точностью eps=0.00001.

    5. Вычислить y = 1 - x2/2! + x4/4! - ... + (-1)n x2n /(2n)! + ... с точностью eps = 0.0001 и сравнить результат с вычисленным через стандартную функцию значением y = cos (x).

    6. Найти произведение цифр заданного натурального числа.

    7. Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа.

    8. Определить номер первого из чисел sin x, sin(sin x), sin(sin(sin x)), .. , меньшего по модулю 10-3.

    9. Дана непустая последовательность различных целых чисел, за которой следует нуль. Определить порядковый номер и величину наиболь­шего среди отрицательных чисел этой последовательности.

    10. Вычислять периметры и площади прямоугольных треугольников по длинам катетов, пока один из заданных катетов не окажется нулевым.

    11. Дана непустая последовательность положительных целых чисел, за которой следует отрицательное число (это признак конца последова­тельности). Вычислить среднее геометрическое этих чисел.

    12. Дана непустая последовательность ненулевых целых чисел, за которой следует нуль. Определить, сколько раз в этой последователь­ности меняется знак.

    13. Числа Фибоначчи (fn) определяются формулами

    f0 = f1 = 1; f n = f n-1 + f n-2 при n = 2,3,... .

    Вычислить сумму всех чисел Фибоначчи, которые не превосходят 1000.

    14. Дана непустая последовательность положительных вещественных чисел х1, х2, х3,..., за которыми следует отрицательное число. Вычис­лить величину

    х1 + 2х2 + ... + (N-1)xN-1 + N хN, где N заранее не известно.

    15. Вычислить длины окружностей, площади кругов и объемы шаров для ряда заданных радиусов. Признаком окончания счета является нулевое значение радиуса.

    16. Определить, есть ли среди цифр заданного числа одинаковые.

    17. Определить, является ли заданное натуральное число палиндромом, т. е. таким, десятичная запись которого читается одинаково слева направо и справа налево.

    18. Вычислить наименьшее общее кратное натуральных чисел a и b.

    19. Дано число L. Определить первый отрицательный член последовательности х1, х2, х3,..., где х1= L, xi = tg(xi-1).

    20. Определить, является ли заданное натуральное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, совершенное число 6=1+2+3).
    Задание 3 (программа 5_3)

    Модифицировать программу 4_1 с использованием оператора цикла с постусловием do … while и сравнить с полученными результатами в работе 4.
    Лабораторная работа 6

    Программирование алгоритмов обработки одномерных массивов
    Цель работы: научиться разрабатывать и отлаживать программы с использованием регулярных типов (векторов).

    Массив – набор элементов, способных хранить данные одинакового типа. Объявляя массив, необходимо сначала указать тип хранимых данных, имя массива и его размер в квадратных скобках. Размером массива называется количество его элементов.

    <класс><тип><идетификатор>[конст. выраж1][конст. выраж2]…;

    Квадратные скобки здесь обязательны, константное выражение в квадратных скобках задает количество элементов в массиве (размерность) по каждому измерению. Число измерений определяется числом квадратных скобок. Индексирование элементов в языке Си начинается с нуля.

    Пример. Найти значение и номер наименьшего элемента в одномерном массиве. При задании элементов исходного массива типизированной константой СА решения задачи имеет вид (рис.8, а) и используется следующая программа:


    #include

    #include

    void main ()

    {

    int a[10] = {5,2,7,1,8,3,4,5,6,6};

    int i, min, n;

    min = a[0];

    n = 0;

    for (i=0; i<10; i++)

    {

    if (a[i]
    { min = a[i];

    n=i+1;

    }

    }

    printf ("минимальный элемент %d-й равен %d\n ", n, min);

    getch();

    }

    Если элементы массива вводятся с клавиатуры, то СА имеет вид (рис.8,б) и текст программы изменится:

    #include

    #include

    void main ()

    { int a[10];

    int i, min, n;

    printf(“Введите элементы массива: ”);

    scanf ("%d",&a[0]);

    min = a[0];

    n = 1;

    for (i=1; i<10; i++)

    {

    scanf ("%d", &a[i]);

    if (a[i]
    { min = a[i];

    n = i+1;

    }

    }

    printf ("минимальный элемент %d равен n= %d\n ", n, min);

    getch();

    }

    Задание 1

    Начертить структурную схему алгоритма, написать и отладить прог­рамму для одной из следующих задач. В программе 6_1 исходные массивы задать типизированными константами. В программе 6_2 элементы исходных массивов ввести через оператор ввода.

    1. Дан массив из N чисел (N<12). Вычислить среднее геомет­рическое значение.

    2. Дан массив из N чисел (10
    3. Дано 20 чисел. Найти их среднее арифметические значение.

    4. Дано 12 вещественных чисел. Найти порядковый номер того из них, которое наиболее близко к какому-нибудь заданному целому числу Х.

    5. Дана последовательность из 15 целых чисел. Определить коли­чество отрицательных чисел в ней и максимальное число подряд следую­щих отрицательных чисел.

    6. Дано 15 целых чисел. Найти наибольшее из них. Определить, сколько из чисел принимает наибольшее значение.

    7. Дано целое n>1 и вещественные числа x1,x2,..,xn. Вычислить математическое ожидание и дисперсию по формулам

    M= , D= .

    8. Дан массив из N чисел (8
    9. Даны два одномерных массива А и В. Вычислить элементы массива С по правилу: если аi и bi различны, то сi присвоить их сумму, при одинаковых аi, bi в сi переписать соответствующий элемент массива А.

    10. Дано 10 вещественных чисел. Вычислить разность между макси­мальным и минимальным из них.

    11. Дано 10 вещественных чисел. Определить, образуют ли они воз­растающую последовательность.

    12. Дан массив X из n чисел (6
    y = x1 - x2 + x3 - ...- xn-1 + xn .

    13. Дано 18 чисел. Определить, количество элементов, отличных от последнего числа.

    14. Дано 12 чисел. Напечатать сначала все отрицательные , а затем все остальные.

    15. Сформировать одномерный массив из 15 простых чисел.

    16. Дано восемь натуральных чисел. Найти их наибольший общий де­литель.

    17. Дана последовательность натуральных чисел. Вычислить сумму тех из них, порядковые номера (индексы) которых - простые числа.

    18. Дан массив из 20 натуральных чисел. Вычислить сумму тех из них, порядковые номера которых - числа Фибоначчи, определяемые форму­лами f0 = f1 = 1; fn = fn-1 + fn-2 при n = 1, 2 ,3 ,... .

    19. Дан массив X из n чисел. Вычислить:

    y = xn(xn+xn-1)(xn + xn-1 + xn-2)...(xn + ... + x1) .

    20. Дано 24 целых числа. Распечатать их в обратном порядке по шесть чисел в строке.

    Задание 2 (программа 6_3)

    Модифицировать программу 3_2 для функций F1(x) и F2 (x) таким образом, чтобы результаты были сформированы в виде трех одномерных массивов. Выполнить ее и сравнить результаты с полученными в лабора­торных работах 3 и 4.
    Лабораторная работа 7

    Обработка двумерных массивов

    Цель работы: научиться разрабатывать и отлаживать программы с использованием матриц.

    Массив можно представить как ряд или последовательность данных, а можно как таблицу, данные которой распределены по строкам и столбцам. В двумерном массиве, одна размерность соответствует строкам, а вторая столбцам. При объявлении массива каждая размерность представляет собой дополнительный индекс.

    Описание двумерного массива (матрицы):

    <класс><тип><идетификатор>[конст. выраж1][конст. выраж2]…,

    <идетификатор>[конст. выраж1][конст. выраж2]…;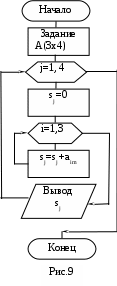




    Пример. Вычислить суммы элементов

    в столбцах двумерного числового массива

    А размером [1..3,1..4].

    Текст программы для СА (рис. 9):

    #include

    #include

    void main ()

    {

    int a [3][4]={{1,2,3,4},{1,2,3,4},{1,2,3,4}};

    int s[4]; // массив сумм

    int i, j; clrscr();

    for ( j=0; j<4; ++j)

    {

    s[j] = 0;

    for ( i=0; i<3; ++i )

    s[j] = s[j] + a[i][j];

    printf (" s[%d] = %d ", j, s[j]);

    }

    getch();

    }

    Задание 1 (программа 7_1)

    1. Даны матрицы A,B [1..4,1..4] вещественных чисел. Вычислить матрицу С поэлементным сложением соответствующих элементов матриц А и В.

    2. Дана матрица B[1..5,1..5] вещественных чисел. Найти для нее транспонированную матрицу.

    3. Даны матрица A[1..4,1..4] вещественных чисел и константа К. Вычис­лить матрицу С=А*К.

    4 . Сформировать массив по правилу 1 0 0 ... 0

    2 1 0 ... 0

    3 2 1 ... 0

    ...

    10 9 8 ... 1 .

    5. Даны натуральное N и элементы квадратной вещественной матрицы А пятого порядка. Вычислить N-ю степень каждого элемента этой матрицы

    (аij1 = аij, аij2 = аij * аij, аij3 = аij2 * аij и т.д., где i, j = 1,2,...,5).

    6 . Сформировать массив по правилу 0 0 0 ...0

    0 1 0 ...0

    0 0 2 ...0

    …

    0 0 0 ...9 .

    7. Сформировать массив последовательностью натуральных чисел:

    1 2 ... 10

    11 12 ... 20

    21 22 ... 30

    ...

    91 92 ... 100 .

    8. Сформировать двумерный массив:

    1 2 3 4 5

    5 1 2 3 4

    4 5 1 2 3

    3 4 5 1 2

    2 3 4 5 1 .

    9. Дана матрица A[1..N,1..N] целых чисел. Сформировать век­тор В из максимальных элементов каждой строки.

    10. Дана матрица A[1..6,1..6] челых чисел и переменная Х. Элементы нечетных строк матрицы А заменить на Х.

    11. Дана матрица B[1..5,1..5]. Получить массив С удалени­ем (либо об-нулением) n-й строки и k-го столбца из матрицы В.

    12. Определить, является ли заданная квадратная матрица девятого порядка магическим квадратом, т. е. такой, в которой суммы элементов во всех строках и столбцах одинаковы.

    13. Определить, является ли заданная целая квадратная матрица шестого порядка симметричной (относительно главной диагонали).

    14. Дана вещественная матрица A[1..7,1..4]. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент оказался в верхнем левом углу.

    15. Дана вещественная матрица размером 4х8. Упорядочить ее стро­ки по неубыванию сумм их элементов.

    16. Для заданной целой матрицы размером 6х8 элементов напечатать индексы всех ее седловых точек. Элемент матрицы называется седловой точкой, если он является наименьшим в своей строке и одновременно на­ибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце.

    17. Дана матрица A[1..6,1..2] вещественных чисел. Рассмат­ривая A [i,1] и A [i,2] как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь кото­рого попадают все эти точки.

    18. Дан массив F[1..N,1..M] из целых малых величин, определить количество «особых» элементов в нем. Элемент считается «особым», если он больше суммы остальных элементов своего столбца.

    19. Дана матрица D[1..5,1..6] из целых чисел. Упорядочить эле­менты строк в нем по убыванию.

    20. Дан массив М координат точек на плоскости. Найти наибольшее расстоя-ние между этими точками.

    Задание 2 (программа 7_2)

    Сформировать таблицу Пифагора.

    Задание 3 (программа 7_3)

    Модифицировать программу 6_3 таким образом, чтобы значения X, F1 и F2 были представлены двумерным массивом, состоящим из трех строк.
    Лабораторная работа 8

    Программирование с применением функций

    Цель работы: научиться разрабатывать и отлаживать программы с использованием подпрограмм (функций).

    Объявление функции (прототип, заголовок) задает ее имя, тип возвращаемого значения и список передаваемых параметров. Определение функции содержит, кроме объявления, тело функции, представляющее собой последовательность операторов и описаний в фигурных скобках:

    [класс] тип имя ([список параметров])[throw (исключения)] {тело функции}

    С помощью необязательного модификатора класс можно явно задать область видимости функции, используя ключевые слова extern, static:

    extern – глобальная видимость во всех модулях программы (по умолчанию);

    static – видимость только в пределах модуля, в котором определена функция.

    Тип возвращаемого функцией значения может быть любым, кроме массива и функции (но может быть указателем на массив или функцию). Если функция не должна возвращать значение, указывается тип void.

    Список параметров определяет величины, которые требуется передать в функцию при ее вызове. Элементы списка параметров разделяются запятыми. Для каждого параметра, передаваемого в функцию, указывается его тип и имя (в объявлении имена можно опускать).

    Механизм возврата из функции в вызвавшую ее функцию реализуется оператором

    return [выражение];

    Пример. Даны три массива A (5), B (5), C (5). Найти среднее арифме­тическое значение наименьших элементов массивов.

    До написания программы разрабатывается СА главной программы (рис.10, а) и СА для подпрограммы нахождения наименьшего элемента в любом массиве (рис.10, б). Отлаженная программа решения задачи имеет следующий вид: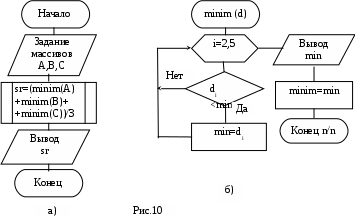




    #include

    #include

    typedef int* mass; // переопределение типа: mass – указатель на целые

    // функция вычисления минимального элемента в массиве

    int minim (mass d)

    {

    int i, min;

    min = d[0];

    for (i=1; i<5; ++i)

    if ( d[i]
    min = d[i];

    printf ("минимальный элемент равен %d\n", min);

    return min;

    }

    void main ()

    {

    int a[] = {5,2,7,1,8};

    int b[] = {3,4,5,6,6};

    int c[] = {3,8,5,2,6};

    int n;

    float sr;

    sr = (minim(a) + minim(b) + minim(c)) / 3;

    printf(" sr= %5.2f ", sr);

    getch();

    }

    Задание 1 (программа 8_1)

    Написать и отладить программы для задач из лабораторных работ 1 и 6 с применением подпрограммы - функции с параметрами. Вычисление функции (или обработку массива) выполнить в подпрограмме, а ввод ис­ходных данных и вывод результатов - в основной программе. Предусмот­реть, по крайней мере, два обращения к функции с различными фактичес­кими параметрами (двумя массивами).

    Для отладки программ использовать средства среды Си (см. прил. А): пошаговое исполнение программы (трассировку) с контролем значений переменных в окне отладчика Watch.

    Задание 2 (программа 8_2)

    1. По заданным вещественным массивам A [1..6], B [1..6] и C [1..6] вычислить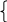

    (max B)/max A + (max C)/max(B+C) при min A < max B,

    max(B+C) + max C в противном случае.

    2. Даны две квадратные вещественные матрицы шестого порядка. Напечатать квадрат той из них, в которой наименьший след (сумма диагональных элементов), считая, что такая матрица одна.

    3. Определить координаты центра тяжести трех материальных точек с массами m1,m2,m3 и координатами (x1,y1), (x2,y2), (x3,y3) по форму­лам

    xc = (m1x1+m2x2+m3x3)/(m1+m2+m3), yc = (m1y1+m2y2+m3y3)/(m1+m2+m3).

    Вычисление координаты оформить функцией с параметрами.

    4. Вычислить все медианы для каждого из трех треугольников по заданным в массивах A, B, C сторонам: ma=0.5 , mb= 0.5 , mc=0.5 . Вычисление медианы оформить функцией.

    5. Даны три одномерных массива вещественных чисел A [1..6], B [1..8] и С[1..7]. Найти общую сумму положительных элементов в масси­вах. Нахождение суммы элементов в массиве оформить функцией.

    6. Даны два двумерных массива целых чисел с размерами (4х5) эле­ментов. Подсчитать количество отрицательных элементов в каждом из них.

    7. Даны два одномерных массива целых чисел A [1..8] и B[1..8]. Найти сумму их максимальных элементов. Для нахождения максимального элемента в массиве использовать функцию.

    8. Даны два двумерных массива целых чисел с размерами (5х5) эле­ментов каждый. Подсчитать произведение элементов главных диагоналей в каждом из них.

    9. Даны три одномерных массива вещественных чисел A[1..6], B[1..8] и С[1..7]. Найти среднее геометрическое значение положитель­ных элементов для каждого.

    10. Даны две матрицы целых чисел M[1..3,0..1], К[1..3,0..2]. Найти среднее арифметическое значение для каждой из них.

    11. Даны три одномерных массива целых чисел A[1..6], B[1..8] и С[1..7]. Подсчитать количество неотрицательных элементов в каждом.

    12. Даны две матрицы целых чисел S[1..3,0..2], К[1..3,0..2], в каждой из которых имеется по два одинаковых числа. Распечатать их значения.

    13. Даны два одномерных массива целых чисел A[1..6] и B[1..8]. Вычислить значение Z=(min A[i] + min B[j]) / min (A[i]+B[j]).

    i j i, j

    14. По заданным целым массивам X[0..7] и Y[8..15] вычислить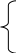

    xi2 при xi yi+8>0,

    yi2 в противном случае.

    15. Дана матрица целых чисел D[1..6,1..5]. Найти наименьшую из сумм неотрицательных элементов строк матрицы. Для вычисления суммы использовать подпрограмму (функцию).

    16. Дана матрица целых чисел E [1..3,1..5]. Используя функцию, найти среднее геометрическое значение для каждого столбца матрицы.

    17. Дана матрица целых чисел F [1..4,1..5]. Найти наименьшие зна­чения элементов в каждой из строк матрицы с помощью функции.

    18. Даны две квадратные вещественные матрицы шестого порядка. Напечатать квадрат той из них, в которой наименьший след (сумма диа­гональных элементов), считая, что такая матрица одна.

    1 9. Сформировать двумерный массив 1 2 3 4 5

    1 4 9 16 25

    1 8 27 64 125

    ... .

    Найти правило и оформить функцией вычисление любой строки.

    20. Даны две матрицы целых чисел V [1..2,1..3], W [1..3,1..2]. Найти суммы элементов строк и столбцов в этих матрицах.

    Лабораторная работа 9

    Программирование с возвратом из функций нескольких значений

    Цель работы: научиться разрабатывать и отлаживать программы с использованием функций, вычисляющих несколько значений.

    Для возврата значений из функции можно использовать два способа. Первый способ заключается в использовании глобальных переменных. Второй способ позволяет возвратить одно значение с помощью оператора return, а другие записать в ячейки памяти с указанными адресами. В последнем случае в функцию необходимо передать адреса ячеек, куда надо помес­тить значения. Это выполняется с помощью указателей.

    Пример 1. Написать программу, функция в которой будет вычислять квадрат и куб аргумента. (Одно значение будем возвращать из функции оператором return, другое будет записываться по указателю int*.)

    # include

    # include // для потоковых функций ввода/вывода

    int fun(int, int*); // прототип функции

    void main()

    {

    int a, kub, qv;

    cin>>a; // ввод из потока

    qv=fun(a,&kub); //исходное число, адрес ячейки,

    куда поместить второе значение

    cout<<"для числа " << a<< "\t квадрат=" <
    nt vvod(int d[])

    {

    int i, k;

    printf("Vvedite chislo elementov ");

    scanf("%d",&k);

    printf("Vvedite massiv is %d elementov \n", k);

    for ( i=0; i
    scanf("%d", &d[i]);

    return k;

    }

    float sr(int k, int f[], double *g)

    {

    int i;

    long int s, p ;

    s = 0; p = 1;

    for ( i = 0; i
    {

    s += f[i]; // s = s + f[i];

    p *= f[i]; // p = p * f[i];

    }

    *g = pow((double)p, 1.0/k);

    return ((float)s)/k;

    }

    void main ()

    {

    int ka, kb, kc; double ga, gb, gc;

    int a[5], b[5], c[5];

    clrscr();

    ka=vvod(a);

    printf("srA = %5.2f \t ", sr(ka,a,&ga));

    printf(" srGA = %5.2f \n", ga);

    kb=vvod(b);

    printf("srA = %5.2f \t ",sr(kb,b, &gb));

    printf("srGB = %5.2f \n", gb);

    kc=vvod(c);

    printf("srA = %5.2f \t ",sr(kc,c, &gc));

    printf("srGC = %5.2f \n", gc);

    getch();

    }

    Задание 1 (программа 9_1)

    Написать и отладить программу для задачи из лабораторной работы 7 с выделением алгоритма обработки или формирования массива. Организовать вызов процедуры с параметрами-массивами для двух наборов исходных данных. (Для ускорения отладки массив можно задать константой).

    Задание 2 (программа 9_2)

    1. Даны массивы A [1..6], B [1..6], C [1..6], вычислить суммы положительных и отрицательных элементов. Получить А*B, B*С, А*C. Вычисление произведения массивов оформить подпрограммой.

    2. Даны массивы A [1..5], B [1..6]. Получить новые массивы путем сдвига элементов в массивах на два разряда вправо, освободившиеся слева элементы обнулить. Сдвиг элементов в массиве оформить подпрограммой, из подпрограммы вернуть выпавшие справа разряды.

    3. Даны два одномерных массива А [1..6] и C [1..6]. Получить A2, С2, А*С. Подсчитать число четных и число нечетных чисел в полученных массивах. Перемножение массивов и подсчет выполнить в подпрограмме.

    4. Даны матрицы целых чисел S[1..3,0..2], K[1..3,0..2], в которых имеется по два одинаковых числа. Найти и напечатать их значения и индексы.

    5. Вычислить значение функции Z = x1+ex2, где x1, x2 - корни уравнения Aix2+Bix+Ci = 0, где i = 1,2,..,N. Коэффициенты уравнения заданы в массивах A [1..N], B [1..n], C [1..N]. Для вычисления корней использовать подпрограмму.

    6. Составить подпрограмму для переменных двух квадратных матриц, с помощью которой вычислить вторую, третью и четвертую степени матрицы M [1..5,1..5]. Для каждой матрицы вычислить сумму и среднее арифметическое значение элементов.

    7. Даны массивы A [1..6], B [1..6], C [1..6]. Преобразовать их, каждому элемен-ту массива, присваивая значение, соседнего с ним справа. Последнему элементу присвоить значение первого. Напечатать исходные, результирующие массивы и отдельно последние два элемента результирующего.

    8. По заданным вещественным массивам A[1..6], B[1..6] и С[1..6] вычислить (minAi)/maxAi + (maxCi)/min(Ci) + max(B+C)I / min(B+C)i.

    9. Даны массивы A [1..6], B[1..8]. Выбрать из них положительные элементы и записать соответственно в массивы A [1..k] и B [1..k], где k<6, n<8; из отрицательных элементов сформировать массивы A2 [1..6-k],B2 [1..8-n]. Напечатать суммы и произведения элементов для каждого.

    10. Даны массивы A [1..6], B [1..6], C [1..6]. Переставить элементы в них таким образом, чтобы слева подряд были записаны отрицательные, а справа положительные, подсчитать количество положительных и число отрицательных в каждом массиве.

    11. Даны две целые квадратные матрицы четного порядка. Элементы массивов с четными номерами строки и столбца заменить нулем (стереть). Напечатать исходные и полученные массивы, количество четных и число нечетных чисел в каждом.

    12. Даны одномерные массивы A[1..6], B[1..8], C[1..10]. Записать их в виде матриц AA [1..3,1..2], BB [1..2,2..4], CC [1..5,1..2], найти наименьшие элементы в каждой и напечатать их номера.

    13. Даны две целые квадратные матрицы шестого порядка. Распечатать элементы главных диагоналей каждой из них и вычислить суммы элементов отдельно главной и побочной диагоналей.

    14. По заданным 10 элементам вещественных массивам A, B и С вычислить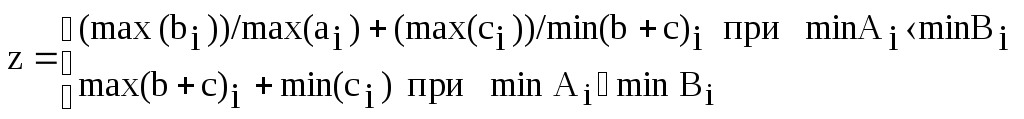



    15. Даны матрицы целых чисел V (-1..2,0..3), W [1..3,0..2]. Сформировать из них одномерные массивы VV и WW, записывая элементы построчно. Напечатать индексы исходных мартиц для максимальных значений.

    16. Дана матрица чисел H [1..5,1..6]. Переставить элементы в строкам матрицы таким образом, чтобы они были расположены в порядке возрастания их модулей. Подсчитать сколько в исходных матрицах положительных и отрицательных чисел.

    17. Дана матрица чисел G [1..2,1..6]. Переставить элементы в матрице так, чтобы элементы каждого столбца матрицы были смещены циклически вправо. Перестановку элементов в столбце реализовать подпрограммой, напечатать два «выпавших» элемента.

    18. Даны массивы A [1..6], B [1..6], C [1..6]. Упорядочить элементы в них в порядке убывания их модулей, напечатать наименьшее и наибольшее значения.

    19. Даны две матрицы целых чисел V [1..2,1..3], W [1..2,1..3]. Найти общие суммы элементов строк, из функции вернуть две суммы.

    20. Даны две целые квадратные матрицы шестого порядка. Вычислить суммы элементов выше главной диагонали и ниже нее. Определить, можно ли отражением относительно главной диагонали преобразовать одну в другую.
    1   2   3   4   5   6   7   8

    написать администратору сайта