Определить собственные значения и собственные векторы матрицы третьего порядка.. Раздел 1. Задача 1. Решение. Задана квадратная матрица А. Ненулевой вектор Х
 Скачать 27.61 Kb. Скачать 27.61 Kb.
|
|
З А Д А Н И Е 1 Аналитическая геометрия Раздел №1. Задача 1. Вариант 20. Дано: А= 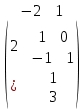 Определить собственные значения и собственные векторы матрицы третьего порядка. Решение. Задана квадратная матрица А. Ненулевой вектор Х= 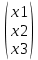 называется собственным вектором матрицы А, если существует такое ненулевое число λ, что AX=λX. Число λ при этом называется собственным значением вектора Х относительно матрицы А. Матрица А-λЕ называется характеристической матрицей матрицы А, многочлен IA-λEI называется характеристическим многочленом матрицы А, уравнение IA-λEI =0 называется характеристическим уравнением матрицы А. называется собственным вектором матрицы А, если существует такое ненулевое число λ, что AX=λX. Число λ при этом называется собственным значением вектора Х относительно матрицы А. Матрица А-λЕ называется характеристической матрицей матрицы А, многочлен IA-λEI называется характеристическим многочленом матрицы А, уравнение IA-λEI =0 называется характеристическим уравнением матрицы А.Собственными числами матрицы А являются корни характеристического уравнения IA-λEI =0 и только они. А= 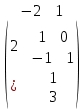 . .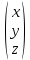 = =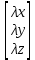  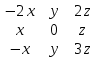 = =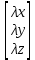 Составляем систему для определения координат собственных векторов: (-2 - λ)x + 1y + 2z = 0 1x + (0 - λ)y + 1z = 0 -1x + 1y + (3 - λ)z = 0 Составляем характеристическое уравнение и решаем его. 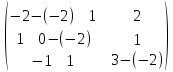 =0 =0
Для этого находим определитель матрицы и приравниваем полученное выражение к нулю. (-2 - λ) • ((0 - λ) • (3 - λ)-1 • 1)-1 • (1 • (3 - λ)-1 • 2)+(-1 • (1 • 1-(0 - λ) • 2)) = 0 После преобразований, получаем: -λ3+λ2+6*λ = 0; -λ(λ2 – λ – 6) = 0; 1) λ2 = 0; 2) λ2 – λ – 6 = 0; λ1= -2; λ3 = 3. Распределим собственные значения матрицы по порядку возрастания: λ1= -2; λ2 = 0; λ3 = 3. а) Для отыскания собственного вектора подставим найденные значения λ2 = -2 в систему уравнений: (-2 – (-2))x + y + 2z = 0 x +(0-(-2)y + z = 0 -x + y +(3-(-2)z = 0 Решим полученную систему методом Гаусса. Выпишем основную матрицу этой системы. 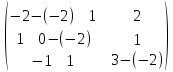 = = 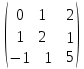
Меняем 1-ую и 2-ую строку местами, Третью строку разделим на 3: 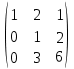 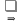 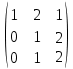
В матрице 2-ая и 3-я строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. 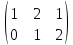
Найдем ранг матрицы: rang(A) = 2 Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно. Этот минор является базисным. Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид: 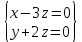 Система имеет множество решений 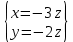 Зададим: Пусть 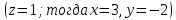 Собственный вектор: X= 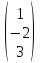 б) Для отыскания собственного вектора подставим найденные значения λ=λ2 =0 в систему уравнений: (-2 – 0)x + y + 2z = 0 x +(0-0)y + z = 0 -x + y +(3-0)z = 0. Решим полученную систему методом Гаусса. Выпишем основную матрицу этой системы. 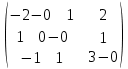 = = 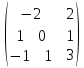 ; ;
Умножим вторую строку на (2). Добавим 2-ую строку к 1-ой; Добавим 3-ю строку ко второй 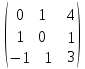  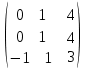 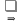 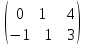 ; ;
Найдем ранг матрицы: rang(A) = 2 Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно. Этот минор является базисным. Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид: 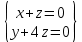 Система имеет множество решений 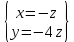 Зададим: Пусть 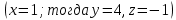 Собственный вектор: X= 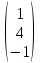 в) Для отыскания собственного вектора подставим найденные значения λ=λ3 =3 в систему уравнений: (-2 – 3)x + y + 2z = 0 x +(0-3)y + z = 0 -x + y +(3-3)z = 0. Решим полученную систему методом Гаусса. Выпишем основную матрицу этой системы. 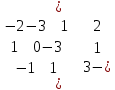 = = 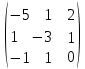 ; ;
Умножим вторую строку на (5). Добавим 2-ую строку к 1-ой; 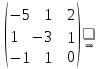 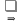 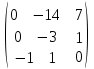 Добавим 3-ю строку ко второй 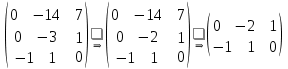 ; ;
Найдем ранг матрицы: rang(A) = 2 Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно. Этот минор является базисным. Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид: 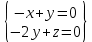 Система имеет множество решений 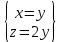 Зададим: Пусть 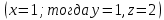 Собственный вектор: X= 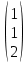 Ответ: Собственные значения: λ1 =-2; λ2 =0; λ3 =3; Собственные векторы: X1 = 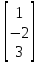 ; X2 = ; X2 = 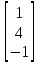 ; X3 = ; X3 = 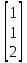 . . |
