Индуктивность. Методические указания к выполнению лабораторной работы по физике для студентов всех специальностей всех форм обучения
 Скачать 1.17 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Саратовский государственный технический университет ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ КАТУШКИ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА Методические указания к выполнению лабораторной работы по физике для студентов всех специальностей всех форм обучения Электронное издание локального распространения Одобрено редакционно-издательским советом Саратовского государственного технического университета САРАТОВ-2006 Все права на размножение и распространение в любой форме остаются за разработчиком. Нелегальное копирование и использование данного продукта запрещено. Составитель - Царев Вячеслав Павлович. Под редакцией - Зюрюкина Юрия Анатольевича. Рецензент - Никишин Евгений Леонардович. 410054, Саратов, ул. Политехническая 77, Научно-техническая библиотека СГТУ, тел. 52-63-81, 52-56-01 http: // lib.sstu.ru Регистрационный номер 060542Э © Саратовский государственный технический университет 2006 г. Цель работы: изучение поведения соленоида в цепях постоянного и переменного тока, экспериментальное определение индуктивности катушки с вдвигающимся в нее ферромагнитным сердечником. Явление электромагнитной индукции. |
 , | (1) |
где
.
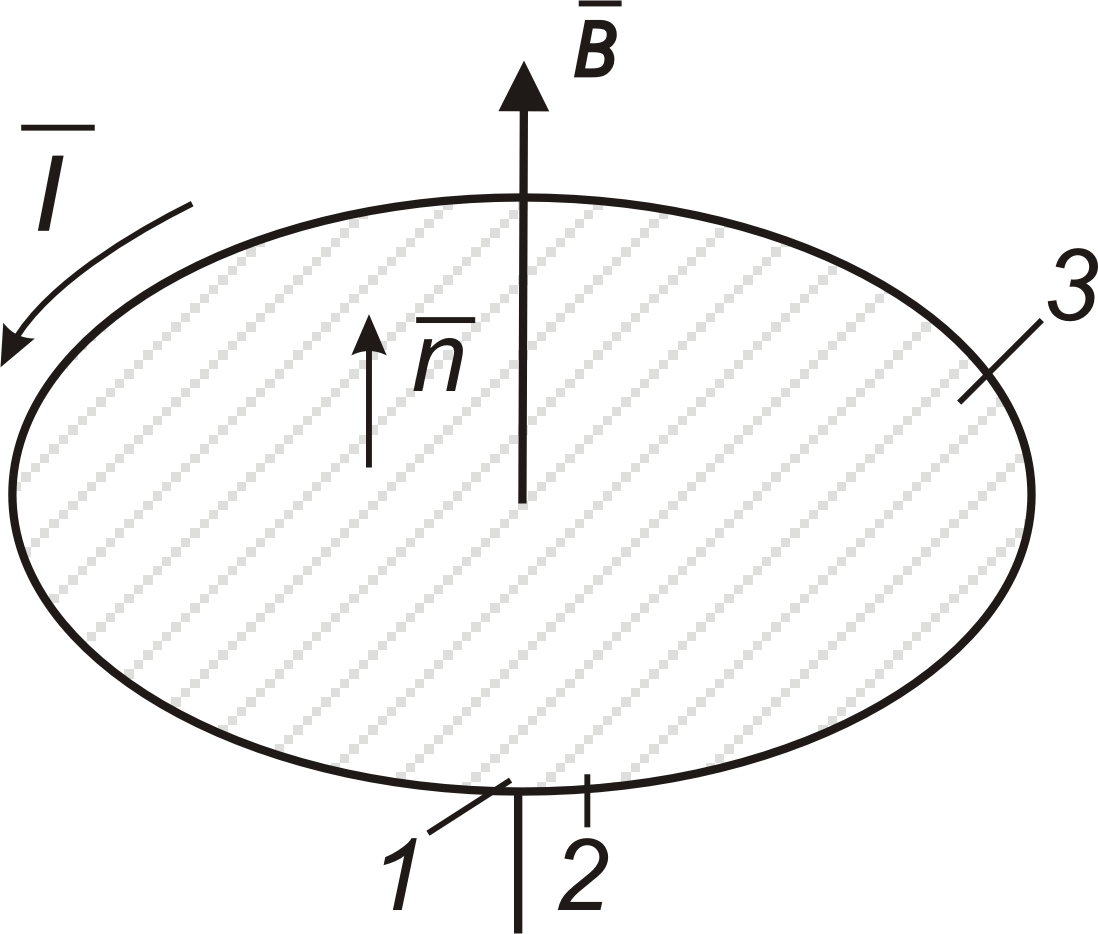
рис. 1
При этом поток магнитной индукции может изменяться как в результате движения контура в постоянном магнитном поле, так и за счёт изменения индукции магнитного поля во времени, когда контур неподвижен. В первом случае индукционный ток вызывается магнитной составляющей силы Лоренца. Но какая же сила возбуждает индукционный ток в неподвижном контуре? Ответ на этот вопрос был дан Максвеллом. Согласно его выводу, всякое переменное магнитное поле возбуждает в окружающем пространстве переменное электрическое поле. Согласно Фарадею, электромагнитная индукция состоит в возбуждении электрического тока при наличии замкнутого проводника. Максвелл же определил сущность электромагнитной индукции, прежде всего в возбуждении электрического поля, а не тока. При этом электрическое поле производит различные действия, например, оно может поляризовать диэлектрик, вызвать пробой конденсатора, может создать ток как в замкнутом, так и в незамкнутом проводнике. Формулировка закона индукции Максвелла является более общей, чем формулировка Фарадея. Математически закон индукции в понимании Максвелла выражается формулой (1), где S – произвольный математический замкнутый контур, который может быть проведён в проводнике, в диэлектрике и т.д.
Знак минус в соотношении (1) выражает правило Ленца: индукционный ток направлен таким образом, что создаваемый им поток через поверхность противодействует изменению внешнего магнитного потока, которое вызывает появление индукционного тока в контуре. Если внешнего магнитного поля нет, а по контуру течёт переменный ток I, то он вызывает появление переменного собственного магнитного поля. Изменение магнитного потока индуцирует ЭДС не только в других проводниках, но и в самом контуре, создающем это магнитное поле. Это явление называется самоиндукцией. Самоиндукция особенно сильно проявляется при замыкании или размыкании цепей. Она препятствует скачкообразному изменению тока. Поток самоиндукции пропорционален току:
 , | (2) |
а закон Фарадея (1) переписывается в виде:
 . | (3) |
Коэффициент пропорциональности L в формулах (2) и (3) является электрической характеристикой данного контура и называется индуктивностью контура.
Значение величины L зависит от геометрической формы контура, его размеров и относительной магнитной проницаемости среды
, в которой находится контур. Например, индуктивность соленоида длиной l, с общим числом витков N и площадью одного витка S определяется формулой:  . | (4) |
Из соотношения (3) видно, что величина индуктивности контура численно равна ЭДС самоиндукции в контуре при изменении в нем силы тока на единицу за одну секунду (
при 
). Это определяет ФИЗИЧЕСКИЙ СМЫСЛ понятия индуктивности контура E. Она является мерой "инертности" контура по отношению к изменению тока в нем. В этом смысле индуктивность L контура в электродинамике играет такую же роль, как масса или момент инерции в механике. За единицу измерения индуктивности L в системе СИ принимается индуктивность такого контура, в котором при силе тока в 1А возникает магнитный поток Ф, равный 1Вб (вебер). Эту единицу называют генри (Гн). Если электрическая цепь содержит несколько индуктивностей, последовательно соединенных друг с другом, то эквивалентная индуктивность определяется формулой:
В случае параллельного соединения нескольких индуктивностей в цепи зависимость приобретает вид:
Векторные диаграммы
В данной лабораторной работе для определения индуктивности катушки используется переменный электрический ток, значение которого изменяется во времени по гармоническому закону. Гармонические колебания можно представить в виде проекции точки равномерно движущейся по окружности. Представление гармонических колебаний с помощью вращающихся векторов называется векторной диаграммой. Если вектор А вращается с угловой скоростью вокруг центра против часовой стрелки, то проекция конца этого вектора на ось ОХ совершает гармоническое колебание вдоль оси X. Уравнение этого колебания:
.Вращающийся вектор
называется вектором амплитуды. Угол поворота вектора 
в данный момент времени t численно равен фазе колебания за данный промежуток времени. Если имеется два колебания, которые происходят с одинаковой круговой частотой 
и с разностью фаз 
, то их можно изобразить с помощью двух векторов амплитуды 
и 
расположенных под углом друг к другу (рис. 2). В этом случае точки 
и 
колеблются с разностью фаз . Принято изображать положение векторов амплитуды в начальный момент времени считая, что их вращение происходит против часовой стрелки (рис. 3).  |  |
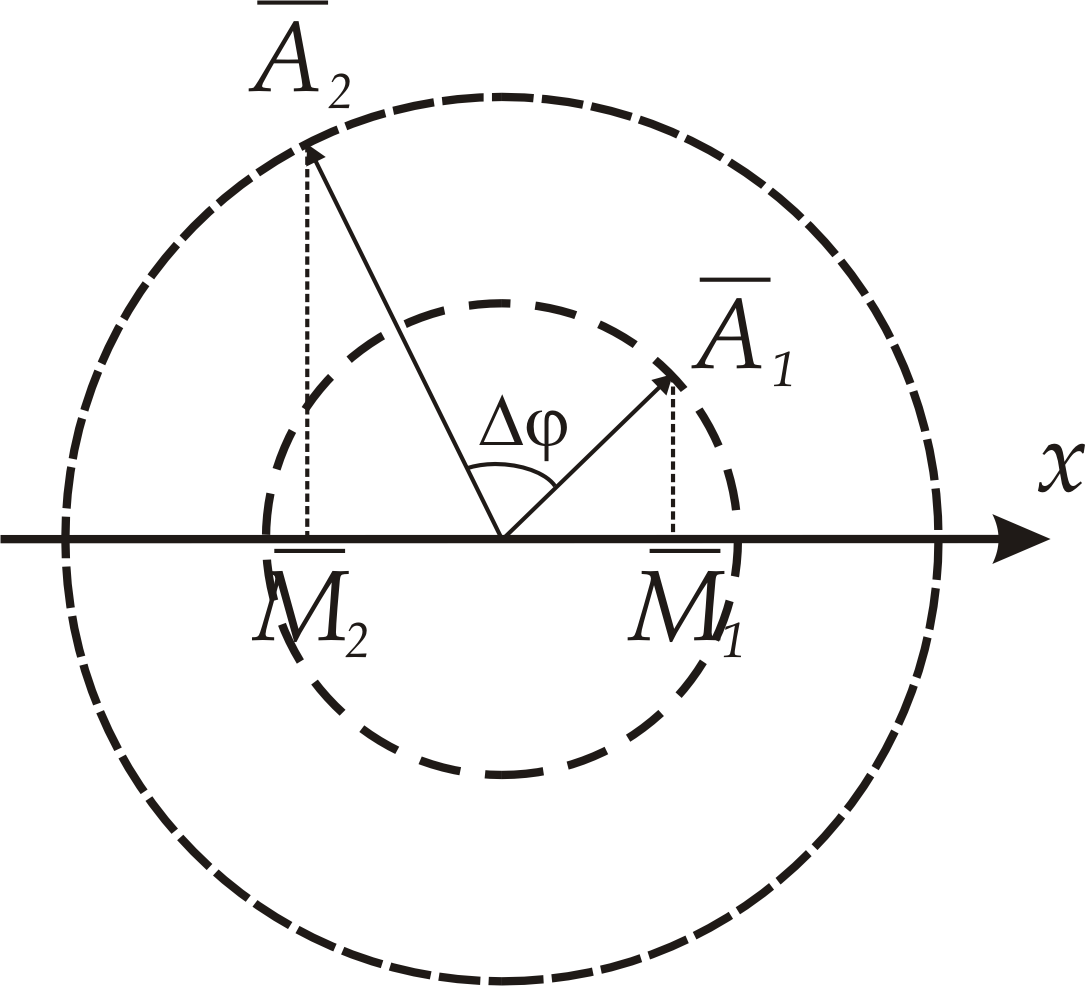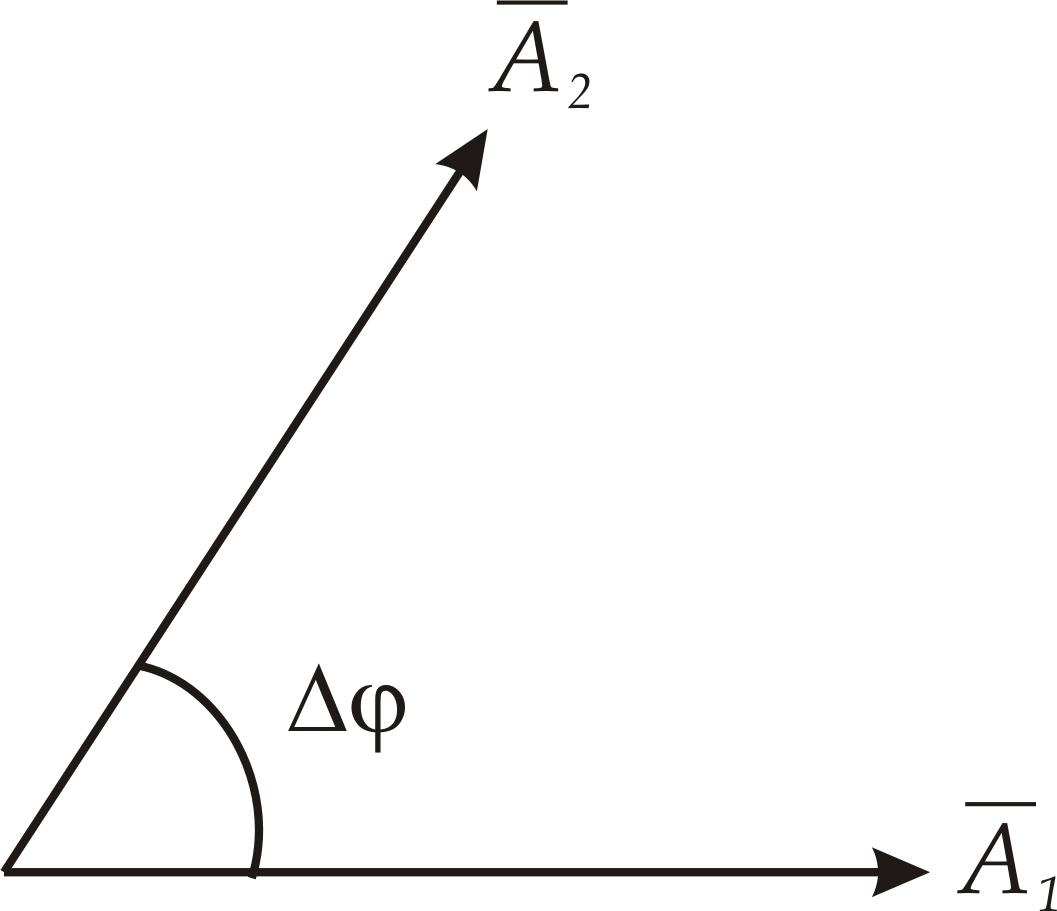| рис. 2 | рис. 3 |
Катушка индуктивности в цепи переменного тока
Если в цепи, содержащей только индуктивность (R=0, C=0), приложено переменное напряжение, то в ней потечет переменный ток
, вследствие чего возникнет ЭДС самоиндукции.
.Закон Ома для такого участка цепи (рис. 4) будет иметь вид:
.или:
 | (5) |
Между напряжением и током в цепи, содержащей только .индуктивность, возникает разность фаз (сдвиг фаз) равная
, т.е. напряжение опережает ток на 
(или Т / 4).
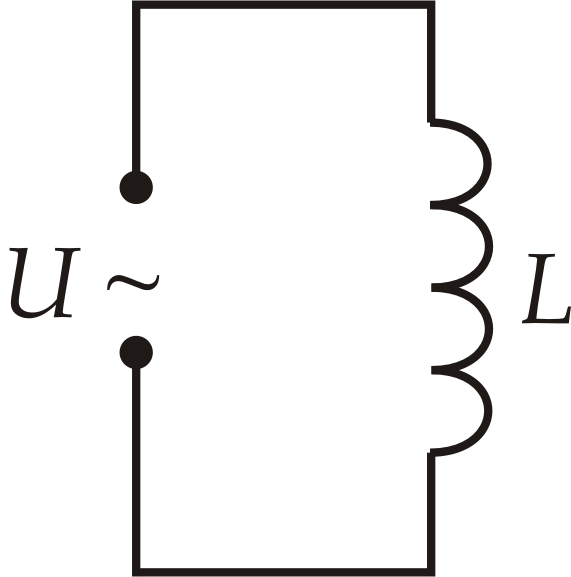
рис. 4
Очень наглядно полученный результат можно изобразить на векторной диаграмме (рис. 5).
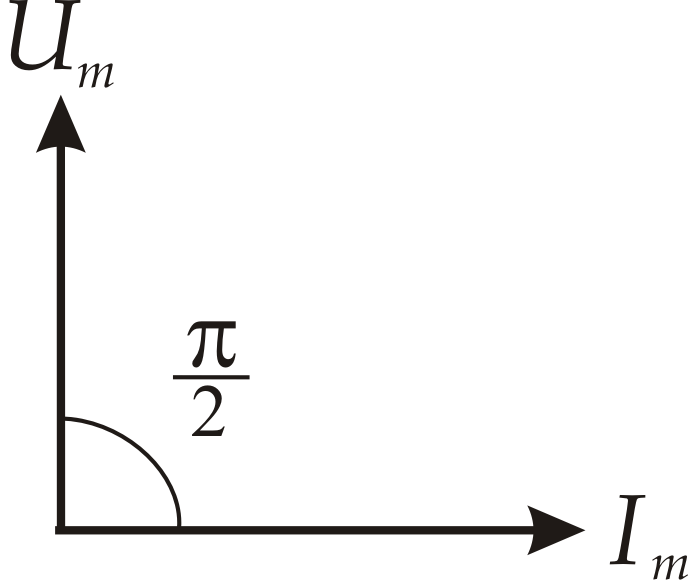
рис. 5
Горизонтальную ось примем за ось токов. Отложим вдоль этого направления вектор тока, численно равный амплитудному значению тока
. Так как напряжение опережает ток по фазе на , то вектор 
повернут относительно оси токов на против часовой стрелки. Из равенства (5) следует, что амплитуда напряжения 
. Разделив правую и левую части этого выражения на 
, получим закон Ома для цепи с индуктивностью:
,где
и 
– эффективные (действующие) значения напряжения и тока.На практике обычные вольтметры и амперметры в цепи переменного тока показывают не амплитудные (максимальные) значения тока и напряжения, а именно эффективные значения, которые в
раз их меньше. Таким образом, из закона Ома мы видим, что величина 
играет роль сопротивления переменному току и называется индуктивным сопротивлением 
. Последовательное соединение резистивного, индуктивного
и емкостного элементов в цепи переменного тока
Обычно реальная электрическая цепь представляет собой достаточно сложную комбинацию индуктивного, емкостного и омического сопротивлений. Рассмотрим простой случай последовательного соединения индуктивности, емкости и резистора (рис. 6).
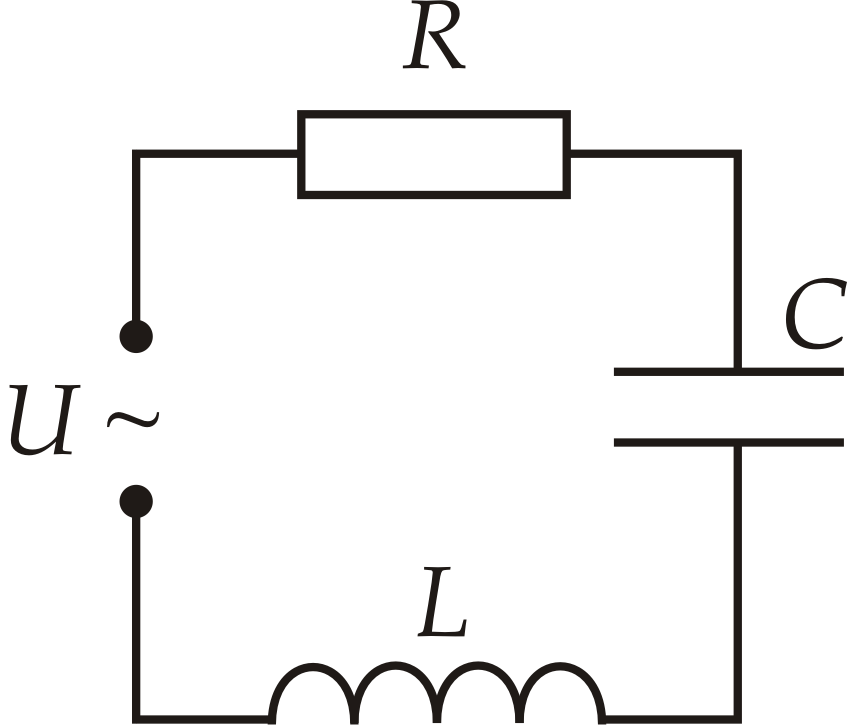
рис. 6
Согласно второму закону Кирхгофа, уравнение для мгновенных значений напряжений в такой цепи имеет вид:
 | (6) |
Так как в данном случае общим для всех участков цепи является ток, то целесообразно выбрать его начальную фазу, равную 0. Известно, что напряжение на резистивном элементе совпадает по фазе с током цепи, на индуктивном элементе напряжение опережает ток на угол
, а напряжение на емкости отстает от тока на угол . Тогда, выразив напряжение через ток и соответствующие сопротивления участков цепи, получим:
 | (7) |
Амплитудное значение напряжения, приложенного к цепи Umравно векторной сумме напряжений на всех элементах цепи, то есть
Um =UR m +ULm+ UCm.
Сложение этих трёх векторов легко провести на векторной диаграмме. Треугольник ОАВ на векторной диаграмме напряжений (рис. 7) называют треугольником напряжений.
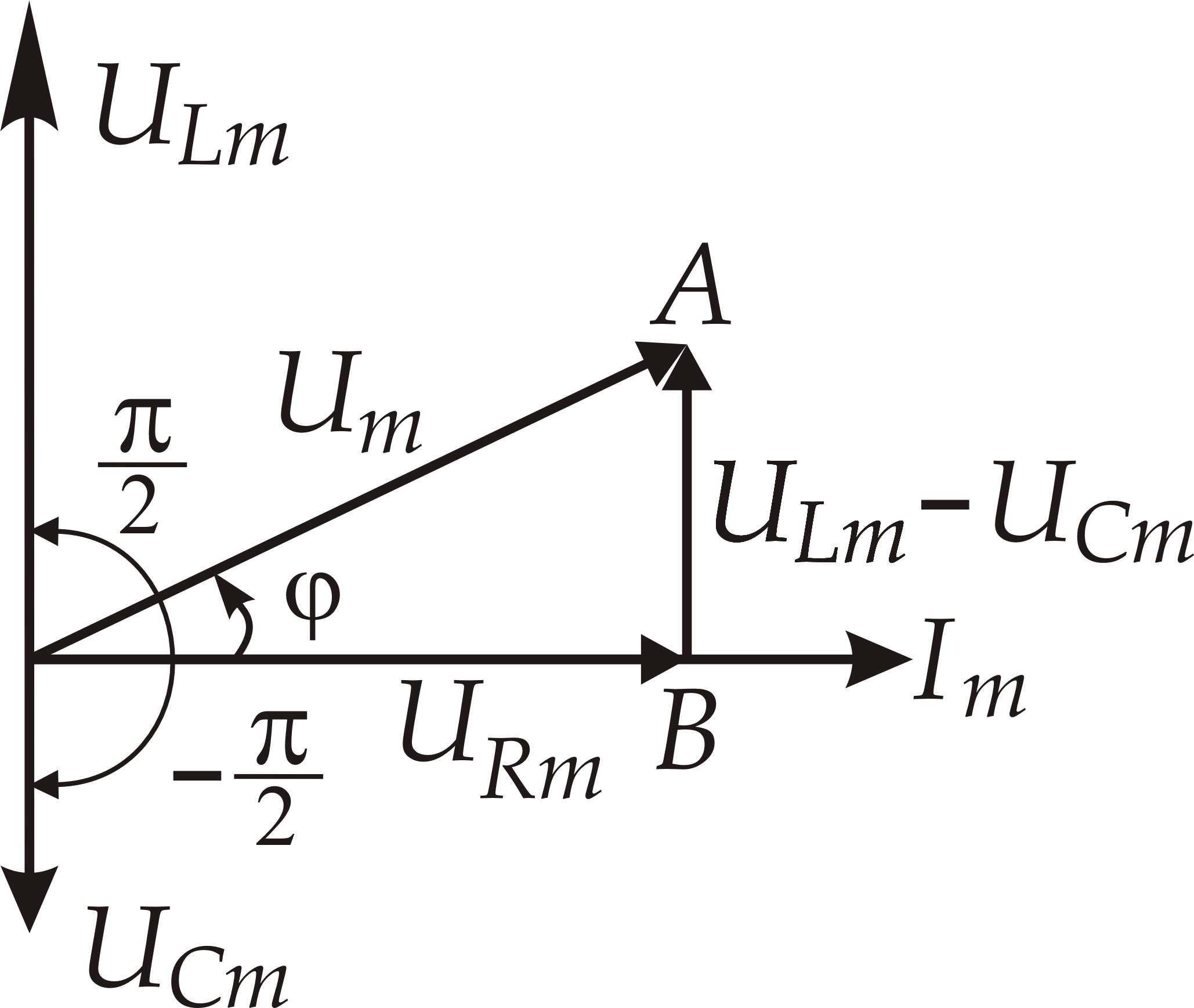
рис 7
В общем виде выражение для мгновенного значения напряжения в цепи в зависимости от значения L или C можно записать так:
. С учетом этой записи уравнение (7) принимает вид:  | (8) |
Полагая вэтом уравнении
, получаем выражение:  | (9) |
При
, получаем:  , | (10) |
где:
– называется реактивным сопротивлением цепи.Возведя равенства (9, 10) каждое в квадрат, а затем, сложив их вместе, получим:
, откуда находим:  , | (11) |
Величина
называется полным сопротивлением цепи переменному току.Разделив левую и правую части равенства (11) на
, найдем связь между током и напряжением, т.е. закон Ома для цепи с последовательным соединением R, L, С.  . | (12) |
Рассмотрим треугольник напряжений на рис 7 и величину напряжения каждой его стороны разделим на ток
, тогда получим треугольник сопротивлений (рис. 8а).Стороны треугольника сопротивлений представляют собой отрезки, т.к. сопротивления не векторные величины. Умножая величины напряжений каждой стороны треугольника сопротивлений на ток
, получим треугольник мощностей (рис. 8б).
рис. 8
На рис. 8 изображены треугольник сопротивлений и мощностей для случая, когда
. Из треугольника мощностей и сопротивлений легко найти связь между различными параметрами цепи. В электротехнике большую роль играет
- коэффициент мощности цепи, который можно определить как
(13)где Р - активная мощность цепи, измеряемая в Вт.,
S – полная мощность цепи, измеряемая в ВА.
Реальные конденсаторы и катушки индуктивности обладают активным сопротивлением. Потери энергии в них обусловлены нагреванием обмотки катушки, нагреванием сердечника токами Фуко и работой по его перемагничиванию, а также нагреванием диэлектрика конденсатора в переменном электрическом поле. Обычно для учета потерь каждый из этих элементов представляют состоящим из двух последовательно соединенных элементов – чисто реактивного и чисто активного. Это позволяет пользоваться выражением (13) для расчета мощности в любой цепи переменного тока.
Лабораторная установка
Схема установки изображена на рис.9. Экспериментальная установка включает в себя два источника питания цепи: один постоянного тока, а второй – переменного.
р
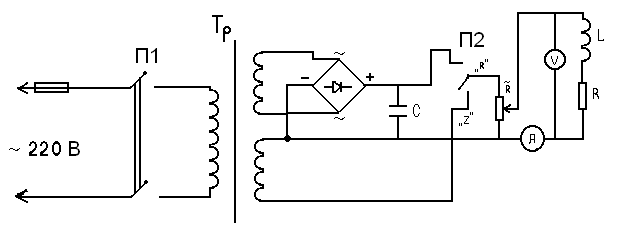
ис. 9.
Регулировка подаваемого на индуктивность напряжения осуществляется потенциометром R. Измерение тока осуществляется амперметром А, а напряжения на катушке индуктивности – вольтметром V. Подключение постоянного или переменного напряжения осуществляется переключателем П2. В установке предусмотрены не показанные на схеме из-за излишней громоздкости элементы, позволяющие переключать соединения и измерять одним и тем же прибором магнитоэлектрической системы характеристики и постоянного и переменного тока. Причём в режиме измерения переменного тока амперметр и вольтметр включаются соответственно в диагонали мостов, собранных на полупроводниковых диодах. Выпрямитель преобразует синусоидальный ток в пульсирующий (одного направления), среднее значение которого измеряется магнитоэлектрическим прибором.
Методика определения индуктивности катушки и обработка результатов измерения
Если цепь имеет только индуктивное сопротивление ХL = ωL и активное R, а ёмкостное сопротивление отсутствует ХС = 1/ωС = 0, то полное сопротивление цепи равно:
(14)
Этот случай часто реализуется на практике, поскольку применяемые катушки индуктивности кроме индуктивного сопротивления, имеют конечное активное сопротивление, а ёмкостное сопротивление пренебрежимо мало. Индуктивность катушки можно выразить из формулы (14):
(15)
Выражение (15) является рабочей формулой для определения индуктивности. Чтобы воспользоваться рабочей формулой, нужно знать круговую частоту переменного тока ω, полное сопротивление цепи переменному току Z и активное сопротивление R. Круговая частота равна ω = 2πν, где ν=50 Гц. Полное сопротивление Z можно найти из формулы (12),
Z = Uэф/Iэф, (16)
поэтому полное сопротивление можно определить с помощью амперметра и вольтметра, питая цепь катушки переменным током.
Активное сопротивление R можно определить, питая цепь постоянным ком (ω = 0). Как видно из формулы в этом случае Z = R.
R = Uп/Iп. (17)
Обработка результатов измерения состоит в следующем:
На основании результатов измерений следует вычислить величину активного сопротивления катушки по формуле (17) .
Необходимо далее вычислить полное сопротивление катушки без сердечника по формуле (16).
Окончательно следует вычислить индуктивность катушки без сердечника по формуле (15).
Аналогично следует определить индуктивность катушки с введенным сердечником. По рассчитанным значениям необходимо построить треугольник сопротивлений для средних значений R,Z и индуктивности L и найти коэффициент мощности для обеих цепей.
Порядок выполнения работы.
Задание 1. Определение индуктивности катушки с выведенным и с полностью введенным сердечником.
Измерения осуществляются в такой последовательности:
Включить на стенде тумблер «СЕТЬ» (переключатель П1). Стальной сердечник из катушки вывести, для чего рукоятку на приборе справа прижать к корпусу. В положении «R» переключателя П2 зафиксировать ток и напряжение на активном сопротивлении катушки при различных положениях ручки потенциометра R.
В положении «Z» переключателя П2 снять зависимость тока в цепи переменного тока Iэфф от напряжения на катушке Uэфф и произвести определение расчетным путем значений индуктивности.
Вставить в катушку сердечник на всю его длину, что соответствует выдвижению до предела рукоятки сердечника вне корпуса. Снять зависимость тока в цепи переменного тока Iэфф от напряжения Uэфф. и вновь произвести определение расчетным путем значений индуктивности.
Результаты всех измерений свести в таблицу.
Таблица
| № опыта | U0 B | I0 A | R Ом | Uэфф В | Iэфф А | Z Ом | ωi рад/с | L Гн | Lср Гн |
| Без сердечника 1 2 3 | | | | | | | | | |
| С сердечником 4 5 6 | | | | | | | | | |
Задание 2 /учебно – исследовательское/. Определение зависимости индуктивности соленоида и коэффициента мощности цепи от длины вводимого в соленоид сердечника.
Здесь предлагается определить экспериментально величину индуктивности катушки для различных длин введенного в соленоид ферромагнитного сердечника (введение сердечника в соленоид следует осуществлять через 1 см.), используя методику определения индуктивности L, представленную в задании 1. По данным измерений построить зависимость индуктивности катушки и значения коэффициента мощности цепи от длины введенного в соленоид сердечника.
Контрольные вопросы
В чём состоит явление электромагнитной индукции? Что такое индукционный ток, ЭДС индукции?
В чём состоит правило Ленца?
В чём состоит явление самоиндукции?
Что такое индуктивность контура, её физический смысл?
Что такое векторная диаграмма?
Докажите, что напряжение на индуктивности опережает ток по фазе на π/2. Нарисуйте векторную диаграмму.
Нарисуйте и объясните векторную диаграмму для цепи, содержащей последовательно включенные омическое сопротивление, индуктивность и ёмкость.
Как выразить полное сопротивление цепи переменному току, постоянному току?
Получите рабочую формулу. Как измерить Ζ цепи?
Что такое коэффициент мощности цепи ?
Литература
1. Савельев И.В. Курс общей физики, т.2 / И.В. Савельев.-М.: Наука, Гл. ред. физ.мат.лит.,2004.
2. Трофимова Т.И. Курс физики / Т.И. Трофимова.- М.: Высшая школа,2002.