06.03.23 Расчетно- лабораторные расчеты. Методические указания по учебной практике для студентов по направлению подготовки

• Название: Методические указания по учебной практике для студентов по направлению подготовки
• Дата: 29.03.2023
• Размер: 0.68 Mb.
• Имя файла: 06.03.23 Расчетно- лабораторные расчеты.doc
• Тип: Методические указания; #1023524
• страница: 1 из 4

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ»
Кафедра «Радиолокация и радионавигация»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО УЧЕБНОЙ ПРАКТИКЕ

Для студентов по направлению подготовки

210400.62 - Радиотехника

МОСКВА 2014

Составители: Е.С. Беспалов, Т.Э. Гельфман, А.П. Пирхавка
Редактор Г.М. Чернявский
В методических указаниях описан порядок прохождения учебной практики, а также приводятся сведения о построении статистических моделей исследуемых объектов, изложена методика расчета энергетики линий связи и рассмотрены принципы компьютерного моделирования в среде приложения Simulink системы программирования MatLab.

Методические указания содержат требования к содержанию отчета о практике.

Соответствуют требованиям Федерального государственного образовательного стандарта по направлению подготовки 210400.62 – Радиотехника и Положению о практике СМКО МИРЭА 7.5.1/02.П.03-12.

Предназначены для студентов очной формы обучения по направлению подготовки 210400.62 – Радиотехника, проходящих учебную практику на кафедре «Радиолокация и радионавигация».

Печатаются по решению редакционно-издательского совета Московского государственного технического университета радиотехники, электроники и автоматики
Рецензенты: Т.И.Болдырева,

Е.М.Лазарев

 МГТУ МИРЭА, 2014

ПОРЯДОК ПРОХОЖДЕНИЯ УЧЕБНОЙ ПРАКТИКИ НА КАФЕДРЕ «РАДИОЛОКАЦИЯ И РАДИОНАВИГАЦИЯ»
Основной образовательной программой высшего профессионального образования подготовки бакалавров по направлению 210400.62 Радиотехника во втором семестре предусмотрена учебная практика.

Целью практики является закрепление теоретических знаний, полученных студентами по одной или нескольким дисциплинам, и ознакомление с особенностями и спецификой профессиональной деятельности по избранному направлению подготовки

Задачами учебной практики является ознакомление с основами будущей профессиональной деятельности, получение сведений о специфике избранного направления подготовки, а также овладение первичными профессиональными умениями и навыками.

Студентам до начала практики выдается задание, как правило, индивидуальное. Рекомендуемая типовая форма задания приведена в Приложении № 1. С целью формирования навыков работы студентов в группе, возможно оформление одного общего задания на несколько студентов (бригаду), при этом определяются отдельные (частные) задания для каждого студента и требования к их соответствующим индивидуальным отчетам.

На студента в период прохождения практики возлагаются следующие обязанности.

До начала практики пройти собеседование с руководителем практики и получить задание на практику.

Строго соблюдать установленные сроки прохождения практики.

Во время прохождения практики: изучить и строго соблюдать правила охраны труда, техники безопасности, производственной санитарии и пожарной безопасности, соблюдать трудовую дисциплину и правила внутреннего трудового распорядка; нести ответственность за выполняемую работу и ее результаты.

Полностью выполнить программу практики в соответствии с заданием на практику.

В течение 2 рабочих дней сообщить руководителю практики об изменении телефона, домашнего адреса, фамилии, а также причину отсутствия на практике, а в случае болезни представить медицинскую справку.

Подготовить отчет, своевременно его сдать и защитить.

Ниже приводится рекомендуемая структура отчета.

Титульный лист (см. Приложение № 2).

Задание на практику (см. Приложение № 1). Рекомендуется включать в отчет лист отметок о прохождении инструктажей и посещения практики.

Обязательными частями пояснительной записки отчета являются:

- содержание;

- введение, которое содержит сведения о предприятии, на котором проходила практика: административное устройство, структура предприятия, взаимодействие его отдельных частей, профиль деятельности, решаемые задачи, а также краткое описание и актуальность индивидуального задания;

- основная часть отчета (техническая, расчетная, исследовательская, конструкторская и т.п.);

- заключение, в котором приводятся основные результаты и выводы;

- список использованной литературы и источников (при необходимости).

При наличии большого количества дополнительных материалов: иллюстраций, таблиц, карт, текстов вспомогательного характера, они выносятся в приложения. Приложения могут быть оформлены отдельной папкой (томом).

Отчет представляется непосредственному руководителю практики в сброшюрованном виде (в папке-скоросшивателе и т.д.).

Работа оформляется в соответствии с требованиями ГОСТов (ГОСТ Р 30 – 2003 и др.). Работа, как правило, представляется в отпечатанном виде.

В зависимости от особенностей задания на практику отчет составляется каждым студентом индивидуально или общий на подгруппу (бригаду) студентов.

1. 
   ПОСТРОЕНИЕ СТАТИСТИЧЕСКОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
   

Цель: получение начальных знаний по математическим моделям - как основы математического моделирования.

Математическая модель – совокупность функциональных зависимостей, описывающих связь между параметрами исследуемой системы (объекта) с учётом влияния окружающей среды и технологических параметров производства. Эта совокупность функциональных зависимостей описывает связь между параметрами только в определённой заданной области параметров и факторов (определение математической модели в широком смысле слова). В соответствии с принятой терминологией под математической моделью следует понимать некоторое математическое выражение, находящееся в отношении подобия к моделируемому объекту (в узком смысле слова). Отношение подобия предполагает однозначное соответствие между двумя объектами: моделью и объектом исследования. Но математическая модель справедлива только в определённой заданной области и учитывает не все явления, происходящие в объекте, поэтому математические модели являются приближёнными, т.е. находящимися в отношении приближённого подобия к моделируемому объекту.

Стремление сделать модель более полной приводит к существенному усложнению, трудности дальнейшего анализа, к потере наглядности. Поэтому в процессе моделирования систем необходимо искать компромисс между сложностью модели и точностью получаемых результатов.

При классификации математических моделей выделяют модели теоретические и статистические, линейные и нелинейные, статистические и динамические, детерминированные и вероятностные.

Математическая модель позволяет:

- получать информацию о процессах, протекающих в объекте;

- рассчитывать, т.е. анализировать и проектировать объекты;

- получать информацию, которую можно использовать для управления моделируемым объектом.

Задание. Построение статистического ряда и гистограммы.

При построении статистического ряда весь диапазон изменения случайной величины x в выборке от x_min до x_max делится на k классовых интервалов. Величину k – можно выбрать по эмпирической формуле
k=1+3,32lg(n) (1.1)
с округлением до ближайшего целого; n – количество опытов.

Длины всех интервалов Δх выбираются одинаковыми
. (1.2)
Затем определяют количество m_j значений случайной величины х в каждом из классовых интервалов [x₁,x₂] и относительную частоту попадания случайной величины в соответствующий интервал
. (1.3)

Статистический ряд оформляется либо в виде таблицы (табл.1.1), либо в виде графика – гистограммы (рис.1.1), причем всем значениям x_j, попавшим вj-й интервал, приписывается значение середины данного интервалаx_jср. Высота гистограммы определяется по формуле:

. (1.4)
Таблица 1.1

Границы j –го интервала	[x1,x2]	[x2,x3]	…	[xk-1,xk]
Число попаданий mj	m1	m2	…	mk
Относительная частота			…

По построенному статистическому ряду вычисляется среднее значение величины x
. (1.5)
Мода M – наиболее часто встречающееся значение случайной величины. Определяется графически по гистограмме (рис.1.1).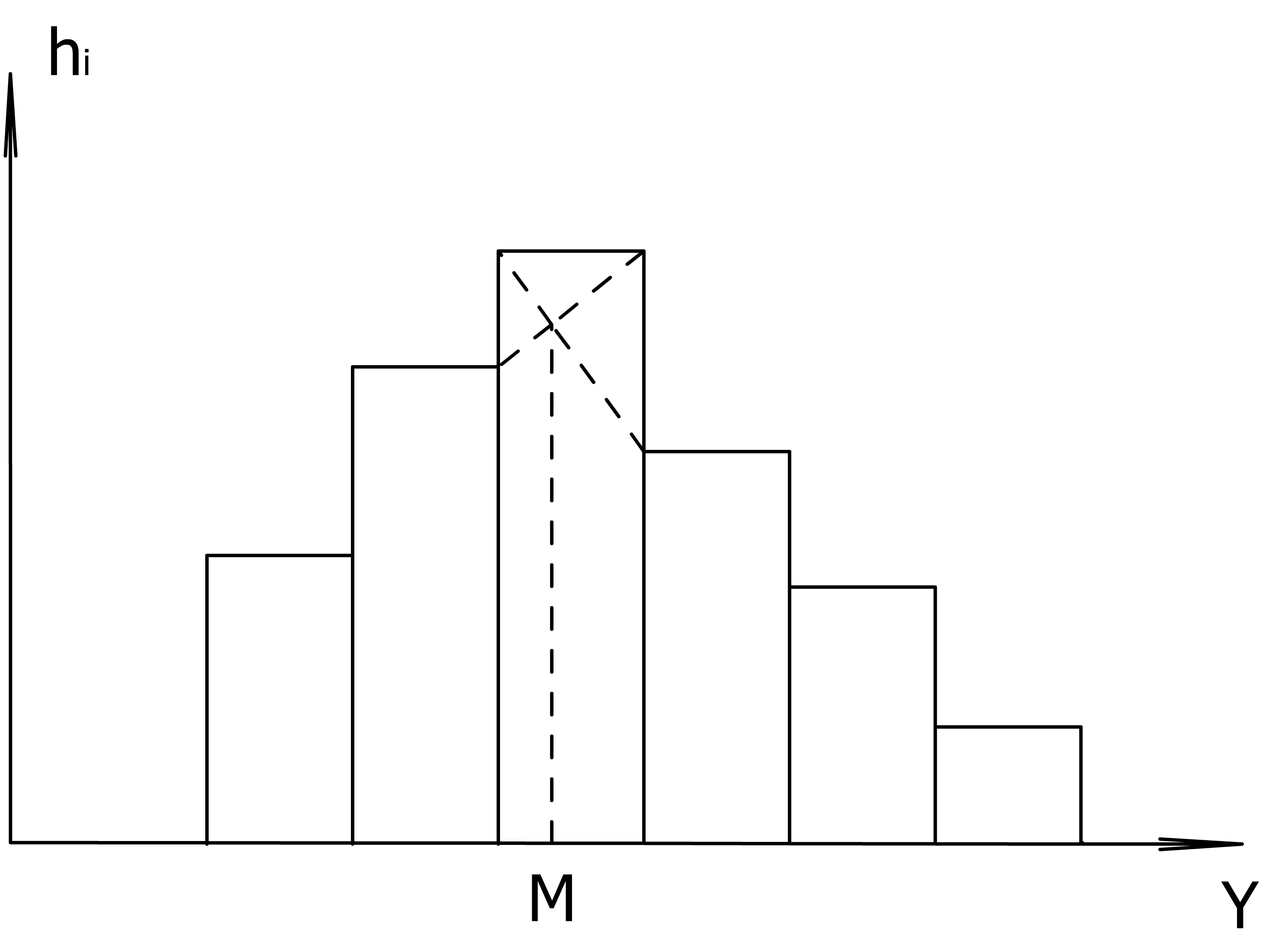


Рис. 1.1


Порядок расчета.

1. Исходные данные приведены в табл.1.2. Вариант задается преподавателем.

2. Рассчитать по формуле (1.1) количество классовых интервалов.

3. Определить по формуле (1.2) длину классовых интервалов.

4. Вычислить границы классовых интервалов.

5. Определить число попаданий m_j величины х в каждый классовый интервал.

6. Рассчитать по формуле (1.3) частоту попадания величины х в каждый классовый интервал.

7. Определить по формуле (1.4) высоту гистограммы.

8. Составить статистический ряд в виде таблицы и гистограммы.

9. Вычислить по формуле (1.5) среднее значение величины х.

10. Графически определить моду.

Отчет должен содержать исходные данные и результаты расчета, а также выводы по работе.
Таблица 1.2

Номер опыта	Номер варианта задания
	1	2	3	4	5	6	7	8
1	41,3	29,1	70,9	19,25	39,0	68,1	59,0	31,2
2	41,2	30,5	85,0	18,34	26,8	69,4	57,1	32,6
3	37,4	35,6	64,0	16,42	32,3	81,6	54,9	26,7
4	35	26,5	89,1	20,06	30,9	72,9	54,1	32,3
5	40,2	27,8	64,5	15,62	27,1	64,5	42,8	24,0
6	48,1	27,6	94,3	18,85	38,6	81,2	55,8	35,1
7	43,5	28,2	75,0	19,15	31,6	75,0	55,1	28,1
8	37	38,1	78,6	15,01	30,5	82,3	47,9	28,2
9	43,6	30,9	83,1	16,12	29,2	72,2	55,9	27,2
10	45,8	33,6	78,5	15,31	28,2	85,4	47,3	24,8
11	45,2	32,3	85,4	19,46	28,6	71,1	52,3	29,2
12	46,8	31,9	92,4	20,3	29,0	79,6	54,6	28,9
13	46,5	28,9	90,4	19,46	37,8	82,2	53,9	30,8
14	34,6	29,8	73,4	19,56	31,6	75,2	51,6	29,8
15	50,8	30,5	68,3	19,76	36,7	77,3	52,9	27,7
16	42,9	30,8	64,3	16,93	31,8	63,8	55,1	30,5
17	35	36,6	87,3	20,7	38,3	83,6	49,3	28,0
18	37	35,5	82,1	16,12	31,1	69,1	45,2	30,5
19	49,8	35,5	90,8	21,0	27,7	69,0	55,6	26,9
20	41,6	34,7	70,7	17,64	27,4	61,0	47,1	29,0
21	44,9	30,6	83,2	14,61	34,2	63,8	48,8	34,5
22	47,1	29,1	89,9	15,01	37,3	67,8	46,1	24,3
23	45,7	35,9	87,6	17,84	27,0	70,6	49,5	25,3
24	39,4	30,1	93,5	15,51	29,6	84,4	46,0	24,5
25	49,3	32	91,7	19,96	32,4	84,3	44,2	33,9
26	42,4	25,6	89,4	16,73	37,0	73,5	44,9	31,8
27	38,5	29,2	69,8	20,7	27,2	64,4	50,8	33,0
28	51,3	30,9	69,8	17,84	34,3	76,6	42,0	29,3
29	44,2	37,4	67,7	15,51	39,1	61,1	58,0	32,7
30	50,7	31	75,8	18,04	29,2	85,9	43,6	33,9
31	37,3	34,2	79,4	21,1	32,9	82,9	40,5	34,2
32	36,6	34,5	85,0	17,13	31,6	66,7	40,1	24,8
33	44,5	33,9	85,3	15,62	27,2	74,7	43,0	35,2
34	50,2	26,6	74,9	17,94	31,7	64,8	56,8	25,9
35	35,2	34,8	85,4	20,3	29,3	84,0	56,3	33,6
36	45,8	29,3	88,4	16,93	37,7	78,6	50,0	28,5
37	36,8	32	77,8	17,33	37,9	65,6	54,6	28,9
38	47,7	30	70,1	15,11	36,5	73,8	56,9	31,9
39	40,9	30,9	68,4	19,76	31,1	63,0	41,0	33,0
40	44,8	27,5	71,6	16,73	38,0	66,7	55,3	24,1
41	43,7	35,2	90,3	20,8	39,4	68,9	42,5	29,8
42	37,8	28,5	78,5	16,73	29,5	69,2	55,9	31,3
43	40,7	25,9	66,7	17,74	27,9	60,8	58,6	24,4
44	47,4	38	86,0	15,01	33,4	69,9	54,3	26,6
45	40,8	37,3	73,4	17,03	30,4	69,0	56,5	33,9
46	49,8	35,1	92,5	16,32	34,4	84,4	52,5	26,2
47	41,9	33,1	84,7	14,61	38,1	60,9	43,5	24,1
48	48,4	26,8	64,7	16,32	39,5	69,0	44,6	31,9
49	46,1	37,5	93,2	17,84	35,0	76,8	41,3	30,3
50	42,3	28,9	67,7	19,25	29,1	67,6	49,2	35,0
Номер опыта	9	10	11	12	13	14	15	16
1	32,2	17,6	78,7	63,9	27,5	14,1	11,8	40,3
2	34,8	23,9	85	56,4	21,5	15,9	12,2	33,1
3	33,1	17,1	64,8	62,3	22	13,2	14,6	31,4
4	33,1	18	64,3	49	23,5	14,1	16,5	36,9
5	24,2	22,8	81,6	47	27,6	16,9	14,3	34,6
6	24,5	22,9	69,9	48,3	25,3	13,6	13,5	33
7	27,2	17,5	75,1	53,9	28	14,2	13,7	27,4
8	26,7	22,8	71,4	45,4	27,3	18,9	15,5	32,3
9	26,5	19,4	86,5	60,8	21,1	13,9	12,6	35,6
10	26	19,3	80,2	56,4	26,1	13,3	12,7	39,1
11	27,7	19	62,2	46,9	27,5	13,2	15,8	29,4
12	32,7	16,1	62,3	61,8	28,6	12,9	12,3	29,6
13	28,7	20,9	68,7	59	26,7	16,9	14,9	28,4
14	32,7	17,5	71,6	48,1	20,9	17	11,5	37,6
15	33,8	22	64,4	60,2	25,2	15,9	15,3	35,4
16	31,4	18,6	84,1	45,1	28,7	18,5	15,5	33,6
17	26,5	17,1	71,3	60,4	25,3	16,9	13	30,6
18	27,5	22,8	83,8	44,6	28,1	18,6	14	36,5
19	24,8	17,5	84,8	45,7	21,3	13,7	13,4	27,2
20	32,2	17,9	71,1	48,1	21,2	16,5	16,5	30,8
21	33,4	22,2	71.6	55,5	26,6	17,5	13,9	27,3
22	30,8	22,9	63,1	54,2	20,4	16,8	14,7	35,1
23	29	18,6	75,5	55,5	20,6	13,7	11,7	32,6
24	25,2	18,1	64,1	46,6	28,9	13,3	16,4	33,8
25	27	23,7	71,8	46,5	24,8	15,1	15,3	31,3
26	27,3	22,8	62,5	48,2	24,5	16,7	16,5	40,3
27	25,2	17,1	82,4	46,2	20,5	15,3	13,2	39,1
28	34,9	18,7	83	51,8	20,6	18,1	12,9	40,3
29	33,7	32,3	85,4	44,7	25,4	18,6	11,5	39,3
30	28,7	19,7	77,6	50	22,1	14,1	15,4	34,5
31	33	19,5	64,3	46,7	24,1	17,5	12,5	34
32	24,4	19,4	86,7	48,5	25,9	14,1	15	39,4
33	29,2	22,7	82,4	52,5	29,7	14	14,6	27,6
34	27,9	16,9	69,3	50,4	23,8	17,9	15,8	40,4
35	33,9	19,1	62,3	58,3	21,1	18,3	14,6	30,7
36	31	21,9	74,4	50,1	27,5	14,7	14	33,3
37	31,8	23,1	69,7	55,5	29,5	19,1	12,8	29,1
38	30,5	17,3	79,4	63,6	20	15,9	12,2	37,2
39	28,7	16,7	63,7	60,7	42,9	14,8	14,1	40
40	24,3	17,1	83	48,4	26,8	18,8	13,9	35,8
41	28,2	16,9	76,4	63	21	13,5	14,1	33,8
42	24,8	23,8	86,6	51,5	23,4	13,3	13	40,7
43	30,2	22,4	67,1	51	25,1	18,5	15,1	35,4
44	25	19,1	63,5	64,1	20,8	17,6	15,1	31,1
45	35,6	18,6	79,2	53,4	24,4	14,7	13,9	39,7
46	28,4	23,8	83,1	47,6	27,4	14,4	15,2	35,1
47	33,1	17,2	75,1	49,1	26,4	16,4	16	30,3
48	28,9	17,3	66,8	60,8	22,2	16,7	15,4	33,4
49	28,1	19,3	87,6	62,4	25,8	16,8	13,8	32,3
50	26,4	16,8	66,4	45,2	25,2	13,3	13,7	34

2. 
   ОПРЕДЕЛЕНИЕ МОЩНОСТИ СИГНАЛА НА ВХОДЕ ПРИЕМНИКА ЛАБОРАТОРИИ КАФЕДРЫ
   

Цель: изучение приборного арсенала лабораторий кафедры и основных факторов, определяющих энергетику радиолиний.

Линии спутниковой связи и вещания состоят из двух участков: передающая земная станция (ЗС) – ретранслятор на искусственном спутнике Земли (ИСЗ) и ретранслятор ИСЗ – приемная ЗС. Мощность сигнала на входе приемника ЗС может быть определена из формулы, которая применяется для расчета любых радиолиний прямой видимости:
, (2.1)
где P_прд – мощность на выходе передатчика ретранслятора ИСЗ,

γ_прд и γ_прм – коэффициенты передачи трактов, связывающих соответственно выход передатчика с передающей антенной на ИСЗ и выход приемной антенны с приемником ЗС,

G_прд и G_прм - коэффициенты усиления передающей и приемной антенн соответственно,

L_o и L_доп – основные и дополнительные потери энергии сигнала в пространстве между ИСЗ и ЗС.

Основные потери L_o обусловлены рассеянием энергии в свободном пространстве при удалении от излучателя
, (2.2)
где λ – длина электромагнитной волны
, (2.3)
f – частота сигнала передатчика, c≈ 3∙10⁸ м/сек – скорость распространения электромагнитных волн,

d – расстояние между ИСЗ и ЗС.

Расстояние d между ИСЗ и ЗС зависит от высоты H орбиты спутника, которая определяет размеры зоны видимости ИСЗ.

Зоной видимости ИСЗ называют часть поверхности Земли, с которой спутник виден в течение заданной длительности сеанса связи под углом места не менее некоторого заданного угла .

Мгновенной зоной видимости ИСЗ называется зона видимости в определенный момент времени, т.е. при нулевой длительности сеанса связи. При движении ИСЗ мгновенная зона видимости перемещается, поэтому зона видимости в течение сеанса связи всегда меньше мгновенной. Размер мгновенной зоны видимости может быть оценен длиной дуги 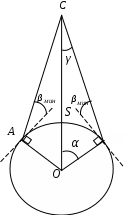или углами и (рис.2.1).