Информатика (методичка). Методическое пособие основы алгоритмизации
 Скачать 1.36 Mb.
|
4. АЛГОРИТМЫ ЦИКЛИЧЕСКОЙ СТРУКТУРЫ4.1. Структура и основные типы циклов В алгоритмах циклической структуры выполнение одних и тех же действий может повторяться несколько раз. Организация циклического вычислительного процесса выполняется в несколько этапов: 1-й этап – подготовка к выполнению цикла. На этом этапе задаются начальные значения для параметра цикла и переменных, использующихся для хранения накапливающихся величин (сумма, количество или произведение вычисляемых величин). Параметр цикла – это переменная, на основе которой строится цикл. Она должна удовлетворять трем условиям: являться исходной величиной для выполнения вычислений; изменяться по определенному закону (чаще всего это закон арифметической прогрессии); оказывать влияние на условие завершения повторяющихся вычислений. 2 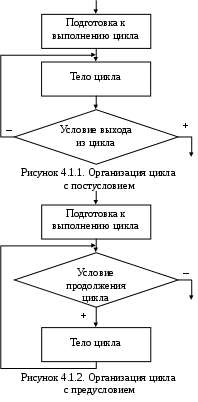 -й этап – тело цикла. Оно содержит арифметические и логические действия, которые могут повторяться определенное количество раз. В конце тела цикла обязательно должен быть блок, в котором изменяется значение параметра цикла.3-й этап – условие выхода из цикла, которое предотвращает бесконечное выполнение цикла. С помощью этого условия проверяется надо ли повторять вычисления, или выходить из цикла. Блок-схема изображающая этапы организации цикла представлена на рис. 4.1.1. Такая организация циклического вычислительного процесса называется циклом с постусловием. В этом случае, после каждого выполнения тела цикла, проверяется условие выхода из цикла. Если оно не выполняется, то происходит возврат на начало тела цикла и повторение вычислений. Когда условие выхода будет выполнено, произойдет завершение работы и выход из цикла. Наличие линии возврата в блок-схеме является основным признаком циклического вычислительного процесса. Кроме цикла с постусловием также существуют цикл с предусловием и цикл «Для». В цикле с предусловием (рис. 4.1.2) перед началом тела цикла проверяется условие продолжения цикла. При этом если условие продолжения цикла является истиной, то выполняются действия, составляющие тело цикла, и происходит переход в начало на проверку условия. Цикл завершает свою работу в том случае если условие продолжения цикла не выполняется – становится ложью. Таким образом, в цикле с постусловием в отличие от цикла с предусловием, тело цикла всегда выполнится хотя бы один раз. Цикл «Для» реализуется на основе блока модификации и представляет собой вариант цикла с предусловием, в котором предполагается, что часть действий по организации цикла выполняется автоматически. Работа цикла «Для» более подробно будет рассмотрена в последующих разделах. Цикл, в состав которого не входят другие циклы, называется простым. П 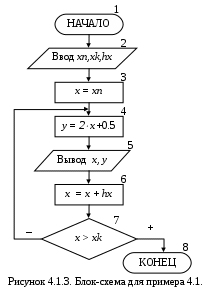 ример 4.1. Составить блок-схему алгоритма, вычисляющего значения функции у = 2∙x + 0.5, при различных значениях х, принадлежащих интервалу 1≤x≤3, hx= 0.5. Для решения поставленной задачи необходимо организовать перебор всех возможных значений х из заданного интервала с указанным шагом (1; 1.5; 2; 2.5; 3). Для каждого полученного х вычислить значение функции у, т.е. организовать циклический вычислительный процесс. Блок-схема алгоритма, в которой используется цикл с постусловием, приведена на рисунке 4.1.3. Исходными данными для решения поставленной задачи являются xn, xk, hx (начальное, конечное значения х из заданного интервала и шаг изменения х), которые вводятся в блоке 2. В нашем случае необходимо будет ввести xn=1, xk =3, hx =0.5. Такая организация ввода исходных данных обеспечивает соответствие блок-схемы двум свойствам алгоритма – определенность и массовость, и в дальнейшем будет называться составлением алгоритма в «общем виде» (все исходные данные должны вводиться, а не присваиваться в процессе выполнения алгоритма). Затем происходит подготовка к выполнению цикла – блок 3, в котором параметру цикла присваивается начальное значение. В качестве параметра цикла выбрана переменная х, удовлетворяющая трем условиям (х является исходным значением для вычислений, изменяется по закону арифметической прогрессии, и оказывает влияние на завершение работы цикла). После этого начинается тело цикла (блоки 4-7). Вычисляется значение y (блок 4). Рассчитанное значение у выводится на экран одновременно с соответствующим значением параметра цикла х (блок 5). Происходит изменение параметра цикла (блок 6), таким образом, получается следующее значение х из заданного интервала. В конце тела цикла стоит условие выхода из цикла x > xk (блок 7), с помощью которого проверяется, не вышло ли новое значение х за правую границу заданного интервала. Если значение х не превышает хk, то происходит возврат на начало тела цикла (блок 4) и повторяются те же самые действия. В случае выполнения условия происходит выход из цикла (переход в блок 8) и алгоритм завершает свою работу. Однократное выполнение тела цикла называется шагом. За один шаг вычисляется одно значение результирующей функции при одном (текущем) значении параметра цикла. Результаты пошагового выполнения цикла, приведенного на рис. 4.1.3, представлены в таблице 4.1. Таблица 4.1. Пошаговое выполнение цикла
Количество шагов выполнения цикла N можно вычислить до начала работы алгоритма по следующей формуле (1):  где ] [ обозначают целую часть выражения. Циклические вычислительные процессы, для которых можно вычислить количество шагов цикла без выполнения алгоритма, называются циклами с известным числом повторений. Для реализации циклов с известным числом повторений можно равноценно использовать любой из трех стандартных типов цикла (с постусловием, с предусловием, «Для»). Если в цикле при выполнении вычислений может возникнуть «аномалия», то завершать выполнение алгоритма, как в разветвляющемся вычислительном процессе, не надо. В этом случае необходимо пропустить все операции, использующие переменную, значение которой невозможно вычислить, и выполнить переход к блоку, в котором изменяется значение параметра цикла, т.е. продолжить работу цикла. При следующем значении параметра цикла «аномалия» может не возникнуть, и работа цикла пойдет естественным путем. 4.2. Алгоритмы нахождения суммы, произведения и количества вычисленных значений Часто наряду с циклическим вычислением значений величины или совокупности величин необходимо определить сумму, произведение или количество всех получаемых значений или некоторых из них. При выполнении суммирования и вычислении произведения или количества рационально использовать принцип постепенного накапливания значений величин, получаемых на каждом шаге цикла. Для хранения таких «накапливающихся» величин используются дополнительные переменные, которым предварительно необходимо задать начальные значения. Обычно это делается на этапе подготовки к выполнению цикла (см. п. 4.1). В качестве начального значения для суммы и количества используется ноль, для произведения – единица. Для пояснения принципа вычисления накапливающихся величин рассмотрим пример аналогичный примеру из п. 4.1. Пример 4.2. Составить блок-схему алгоритма, вычисляющего значения функции у = 2∙x + 1, при различных значениях параметра х, принадлежащих интервалу -3 ≤ x≤ 3, hx= 1. В качестве дополнительной задачи необходимо найти: количество (k) вычисленных значений y, которые ≤ 0; сумму (S) всех значений y(S = y) и произведение (Р) значений y, которые > 0 (  ).При решении этой задачи необходимо организовать перебор всех возможных значений х из заданного интервала с указанным шагом, и для каждого полученного х вычислить значение функции у. Разрабатываемый алгоритм является циклом с известным числом повторений, так как количество повторений вычислений можно определить по формуле (1):  Поэтому для реализации алгоритма, в отличие от примера 4.1, можно воспользоваться циклом с предусловием, блок-схема которого приведена на рис. 4.2. 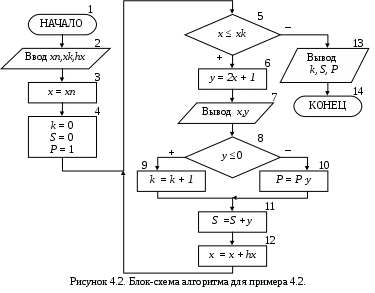 Исходными данными, как и в примере 4.1, являются xn, xk, hx, которые вводятся в блоке 2. В нашем случае необходимо будет ввести xn=-3, xk =3, hx =1. На этапе подготовки к выполнению цикла задаются начальные значения для параметра цикла x (блок 3) и дополнительных величин k, S, P (блок 4). Затем начинается тело цикла с предусловием (блоки 5-12). При входе в цикл проверяется условие продолжения вычислений в теле цикла (блок 5). Вычисляется (блок 6) и выводится на экран (блок 7) значение у при текущем значении параметра цикла х. Затем проверяется вычисленное значение у (блок 8), и если у ≤ 0, то k увеличивается на единицу (блок 9), в противном случае текущее значение у учитывается в произведении Р (блок 10). Кроме этого, каждое вычисленное значение у добавляется к сумме S (блок 11). В конце тела цикла выполняется изменение параметра цикла (блок 12), т. е. вычисляется следующее значение х из заданного интервала, и происходит возврат в начало цикла. После выхода из цикла выводятся значения переменных k, P, S (блок 13). Результаты пошагового выполнения цикла в алгоритме, приведенном на рис. 4.2, представлены в таблице 4.2. Таблица 4.2. Пошаговое выполнение цикла
Пошаговое выполнение цикла показывает, что итоговые значения суммы, количества и произведения (k=3, P=105, S=7) будут получены после завершения работы цикла. Поэтому они должны выводиться только после выхода из цикла. Если вывод k, P, S организовать внутри тела цикла, то будут выведены все промежуточные значения этих величин, приведенные в таблице. Также будет неправильно поставить вывод значения параметра цикла х и вычисляемой величины у (блок 7) после выхода из цикла. Из таблицы 4.2 видно, что в этом случае будут выведены последние значения, хранящиеся в этих переменных (х=4 и у=7). 4.3. Циклы с неизвестным числом повторений При решении некоторых задач может возникнуть ситуация, когда невозможно заранее определить количество повторений вычислений. В таких случаях речь идет о циклах с неизвестным числом повторений. В циклах с неизвестным числом повторений вычислительный процесс завершается при выполнении некоторого дополнительного условия. Значения параметра цикла уже не задаётся в виде диапазона, а только указывается его начальное значение и шаг изменения. Тем не менее, организация цикла выполняется по стандартной методике, указанной в п. 4.1. Отличие заключается в том, что не любой тип циклического вычислительного процесса можно использовать. Тип цикла определяется в соответствии с заданным дополнительным условием завершения вычислений. Это однозначно исключает возможность использование цикла «Для» на основе блока модификации. Для определения количества шагов повторения цикла необходимо организовать счетчик. Пример 4.3. Составить блок-схему алгоритма, вычисляющего значения функции у = ln(1 + 0.2∙x), при различных значениях параметра х, изменяющегося от xn≤ 3 с шагом hx= -2. При этом вычислять у до тех пор, пока выражение под знаком логарифма остается больше 0. Определить количество (k) вычисленных значений y. Перед решением задачи необходимо определить тип цикла, который будет использоваться. Вычисляемое выражение содержит «аномалию» (значение под знаком логарифма должно быть больше 0), которая в тоже время является условием завершения вычислений. Другими словами, необходимо вначале проверить возможность вычисления значения у, а только затем вычислять его. Поэтому в данном случае для организации вычислительного процесса можно использовать только цикл с предусловием (рис. 4.3). В качестве исходных данных вводятся значения переменных хn, hx (блок 2). В блоке 3 задаются начальные значения для параметра цикла x и счетчика количества повторений цикла k. После этого, в блоке 4 одновременно проверяются условие продолжения цикла и возможная «аномалия» (выражение под знаком логарифма должно быть больше 0). В теле цикла для текущего значения х вычисляется и выводится соответствующее значение у (блоки 5-6), а также увеличивается значение счетчика вычисленных у (блок 7). В конце тела цикла выполняется переход к следующему значению параметра цикла х (блок 8). Цикл работает до тех пор, пока под знаком логарифма не появится выражение ≤ 0. После выхода из цикла в блоке 9 выводится переменная k – количество вычисленных значений у. 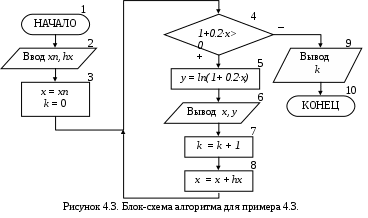 Результаты пошагового выполнения цикла в алгоритме, приведенном на рис. 4.3, представлены в таблице 4.3. Таблица 4.3. Пошаговое выполнение цикла
4.4. Вложенные циклы Решение некоторых задач требует выполнения перебора значений не одной, а нескольких величин одновременно. В этом случае речь идет о применении вложенных циклов, каждый из которых организовывается по стандартному принципу (может быть любого из трех типов) и осуществляет перебор только одного параметра. При этом первый цикл называется внешним, а вложенные в него – внутренними. Причем один и тот же цикл может быть внешним по отношению к одному и внутренним по отношению к другому циклу. Границы внутреннего цикла не могут выходить за границы внешнего по отношению к нему цикла. Для каждого значения параметра внешнего цикла происходит перебор всех возможных значений параметра внутреннего цикла. Другими словами, всегда выполняется в первую очередь самый внутренний цикл. Такая организация циклов дает возможность перебрать значения их параметров во всех возможных комбинациях. Пример 4.4. Составить блок-схему алгоритма, вычисляющего значения функции у = a - 2∙b, для всех возможных комбинаций значений параметров a и b, принадлежащих интервалам 0 ≤ a≤ 2, ha= 1 и -2 ≤ b≤ 2, hb= 2, соответственно. Определить среднее арифметическое (S) вычисленных значений y. Для решения поставленной задачи необходимо организовать два вложенных цикла по перебору параметровa и b. При этом каждый цикл является циклом с известным числом повторений, т. к. заранее можно вычислить количество значений a из заданного интервала (Na = ](2 – 0)/1[ + 1 = 3) и количество значений b из заданного интервала (Nb = ](2 – (-2))/2[ + 1 = 3), а следовательно и общее количество вычисленных значений y (N = NaNb). Значит, для организации циклов можно использовать любой из трех стандартных типов. Кроме этого y одновременно зависит от двух параметров a и b, поэтому не имеет принципиального значения по какому параметру делать внешний цикл, а по какому – внутренний (внешним может быть цикл по параметру a, а внутренним – по параметру b, и наоборот). В случае же если одна из вычисляемых величин зависит только от одного параметра, то цикл по этому параметру рационально сделать внешним и вычислять величины, зависящие только от этого параметра во внешнем цикле. Такая организация позволит избежать многократного вычисления одних и тех же значений во внутреннем цикле. На рисунке 4.4 представлена блок-схема алгоритма, в которой для решения поставленной задачи, используется два вложенных цикла: внешний цикл с предусловием по параметру a и внутренний цикл с постусловием по параметру b. Работа алгоритма начинается с ввода исходных данных (блок 2), которые представляют собой начальные, конечные значения и шаг изменения параметров aи b из заданных интервалов. На этапе подготовки к выполнению внешнего цикла (блок 3) параметру цикла a присваивается начальное значение an, а также о 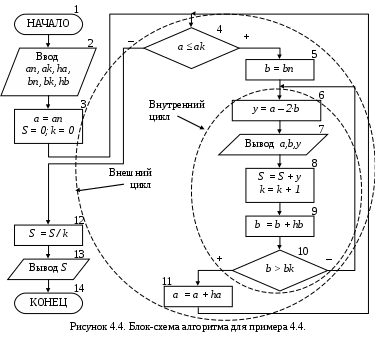 бнуляются переменные S и k, используемые для хранения суммы и количества вычисленных значений y. Тело внешнего цикла с предусловием включает блоки 4-11. Если текущее значение a не выходит за правую границу интервала (блок 4), то происходит выполнение тела внешнего цикла, которое включает в себя внутренний цикл. В блоке 5 происходит подготовка к выполнению внутреннего цикла, его параметру b присваивается начальное значение bn. Тело внутреннего цикла с постусловием включает блоки 6-10. В блоке 6 вычисляется текущее значение y, а в блоке 7 происходит вывод вычисленного y и соответствующих ему значений a и b. В блоке 8 полученное значение у добавляется к сумме S и увеличивается значение счетчика вычисленных у. Затем происходит изменение параметра внутреннего цикла b на значение шага hb (блок 9) и выполняется проверка условия выхода из внутреннего цикла (блок 10). Если текущее значение b не превышает конечного bk, то происходит возврат на начало внутреннего цикла и повторяется вычисление y при новом значении b. В тоже время значение параметра внешнего цикла a остается неизменным. Таким образом, при одном значении параметра внешнего цикла происходит перебор всех значений параметра внутреннего цикла. После выхода из внутреннего цикла в блоке 11 происходит изменение параметра внешнего цикла a на значение шага ha. Затем выполняется переход на начало цикла (блок 4) и повторяются описанные выше действия, пока не завершит работу внешний цикл. После выхода из внешнего цикла в блоках 12-13 вычисляется и выводится S - среднее арифметическое вычисленных значений y. Результаты пошагового выполнения циклов в алгоритме, приведенном на рис. 4.4, представлены в таблице 4.4. Таблица 4.4. Пошаговое выполнение алгоритма с вложенными циклами
Следует также обратить внимание на то, что начальное значение параметра внутреннего цикла b необходимо задавать каждый раз перед началом выполнения вложенного цикла (блок 5), т.е. внутри внешнего цикла. Если это будет сделано одновременно с заданием начального значения для параметра внешнего цикла a (блок 3), то внутренний цикл выполнится только при начальном значении a. На этом алгоритм завершит свою работу и, следовательно, не будут перебраны все возможные комбинации значений a и b. |