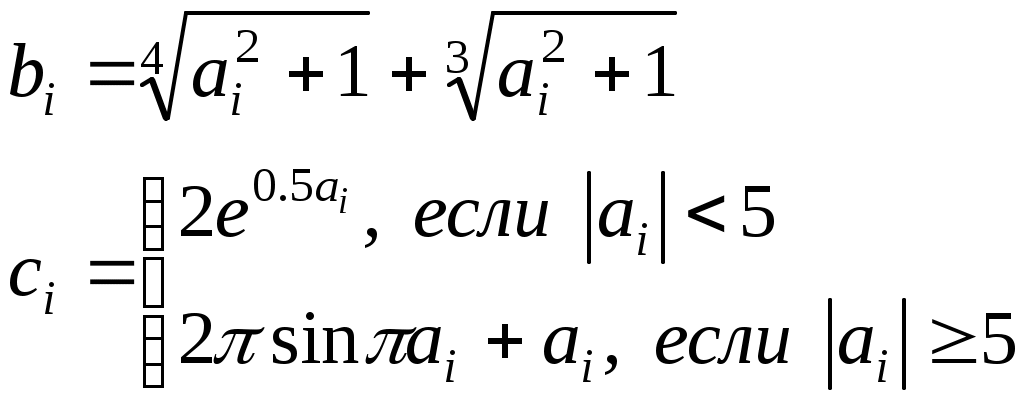Информатика (методичка). Методическое пособие основы алгоритмизации
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
Задание № 4. Организация вложенных цикловЗадание. Составить блок-схему алгоритма и программу решения поставленной задачи, которая в соответствии с исходными данными вычисляет значения заданных выражений. П 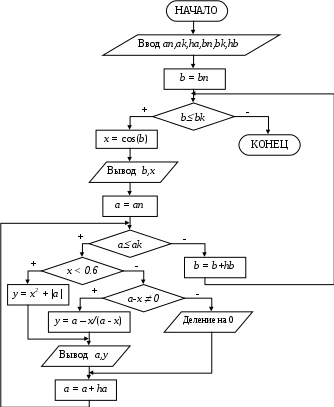 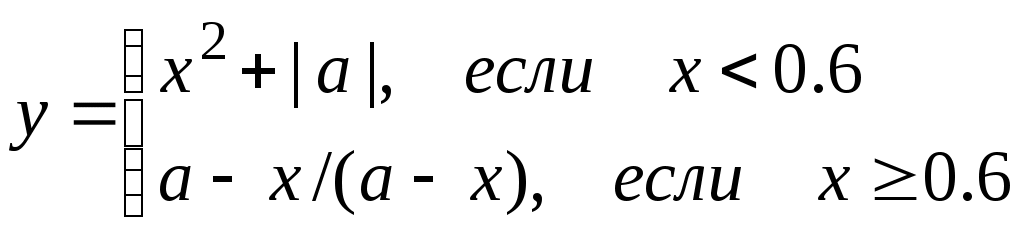 ример. Составить алгоритм и программу для вычисления значений xи у при всех возможных значениях a и b, которые лежат в интервале от an до ak с шагом ha и от bn до bk с шагом hb, соответственно. ример. Составить алгоритм и программу для вычисления значений xи у при всех возможных значениях a и b, которые лежат в интервале от an до ak с шагом ha и от bn до bk с шагом hb, соответственно. Блок-схема алгоритма: Программа на языке Турбо Паскаль: Program Pr4; Label m1; Var a, an, ak, ha, b, bn, bk, hb, x, y: real; Begin Write(‘Ввод an, ak, ha, bn, bk, hb’); Readln(an, ak, ha, bn, bk, hb); b:=bn; While b <= bk do Begin x := cos(b); writeln(‘b=’, b : 6 : 2, ‘ x=’, x : 6 : 2); a := an; While a <= ak do Begin If x < 0.6 Then y := Sqr(x) + Abs(a) Else If a – x < > 0 Then y := a – x / (a – x) Else Begin Writeln(‘Деление на 0’); Goto m1; End; writeln(‘a=’, a : 6 : 2, ‘ y=’, y : 6 : 2); m1: a := a + ha; End; b := b + hb; End; End. Варианты заданий.
Продолжение таблицы к заданию 4
Продолжение таблицы к заданию 4
Продолжение таблицы к заданию 4
Задание № 5. Обработка одномерных массивов Задание. Составить блок-схему алгоритма и программу решения поставленной задачи, которая в соответствии с исходными данными вычисляет значения заданных выражений. Пример. Составить алгоритм и программу формирования массива Y на основе исходного массива Х размерностью N. Определить максимальный положительный элемент массива Y. Элементы массива Y вычисляются по формуле: 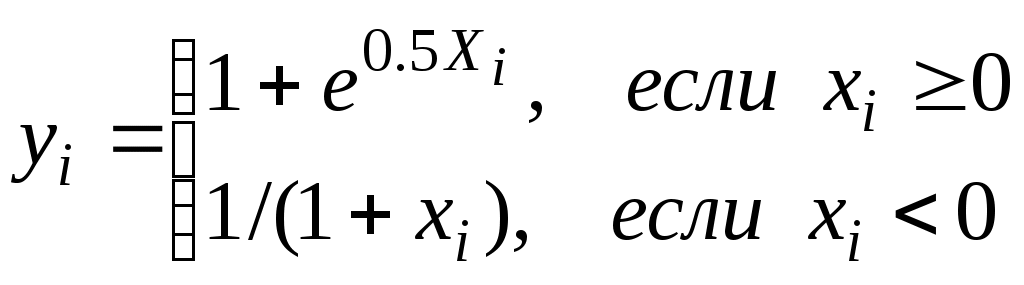 Программа на языке Турбо Паскаль: Program Pr5; Var x, y: array [1..20] of real; i, N, imax: byte; Begin Write(‘Ввод N’); Readln(N); for i:=1 to N do begin Write(‘Ввод x[’, i, ’] =’); Readln(x[i]); end; imax := 0; for i:=1 to N do begin if x[i] >= 0 then y[i] := 1+exp(0.5*x[i]) else if 1+x[i] <> 0 then y[i] := 1/(1+x[i]) else begin writeln(‘Аномалия’); y[i] := 0 end; writeln(‘y[‘, i, ’]=’, y[i] : 6 : 2); if y[i] > 0 then if imax = 0 then imax := i else if y[imax] < y[i] then imax := i; end; 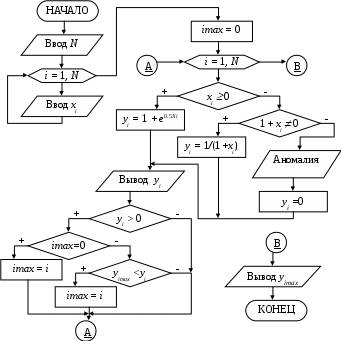 writeln(‘y[’, imax, ‘]=’, y[imax] : 6 : 2); End. Блок-схема алгоритма: Варианты заданий.
Продолжение таблицы к заданию 5
Продолжение таблицы к заданию 5
Продолжение таблицы к заданию 5
Задание № 6. Обработка двумерных массивов Задание. Составить блок-схему алгоритма и программу решения поставленной задачи обработки двумерного массива. Пример. Заменить максимальный элемент матрицы A размерностью MхN суммой элементов, расположенных на периметре матрицы. Блок-схема алгоритма: 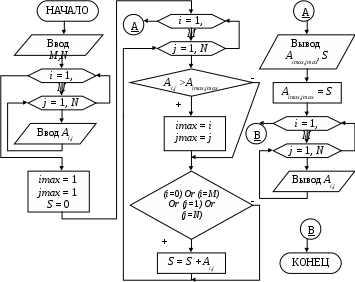 Программа на языке Турбо Паскаль: Program Pr6; Var a: array [1..10, 1..10] of real; i, j, M, N, imax, jmax: byte; S: real; Begin Write(‘Ввод M, N’); Readln(M,N); for i:=1 to M do for j:=1 to N do begin Write(‘Ввод A[’, i, j, ’] =’); Readln(a[i,j]); end; imax := 1; jmax: = 1; S: = 0; for i:=1 to M do for j:=1 to N do begin if a[i,j] >= a[imax,jmax] then begin imax := i; jmax := j; end; if (i=0) Or (i=M) Or (j=1) Or (j=N) then S := S + a[i,j] end; writeln(‘A[‘, imax, jmax, ’]=’, a[imax, jmax] : 6 : 2, ‘ S=’, S : 6 : 2); a[imax, jmax] : = S; for i:=1 to M do begin for j:=1 to N do Write(‘A[’, i, j, ’] =’, a[i,j] : 6 : 2, ‘ ‘ ); writeln end; End. Варианты заданий. 1. Определить номера строки и столбца максимального отрицательного элемента прямоугольной матрицы А= (аi,j)M,N. 2. Найти среднее арифметическое значение элементов прямоугольной матрицы Х=(xi,j)7,3, находящихся на периметре этой матрицы. 3. Сформировать вектор D=(d1,d2,…dM), каждый элемент которого равен среднему арифметическому значений элементов строк матрицы С размерностью MN. 4. В матрице А= (аi,j)M,М элементы главной диагонали заменить «1», если данный элемент больше последующих элементов соответствующей строки, и «0» - в противном случае. Вычислить элементы вектора G=(g1,g2,…gM), как произведение отрицательных элементов соответствующих строк заданной матрицы А размерностью MN. Рассчитать элементы матрицы С=(сi,j)3,3, являющейся произведением матриц А=(ai,j)3,4 и В=(bi,j)4,3. Элементы матрицы С рассчитываются по формуле: Подсчитать количество нулевых элементов матрицы размерностью MN и напечатать их индексы. Первый по счету нулевой элемент заменить суммой положительных элементов. Вычислить элементы матрицы Z размерностью 56 по элементам исходной матрицы Х=(хi,j)5,6. Главную диагональ оставить неизменной. zi,j=x2i,j. Сформировать вектор В=(b1,b2…b7), каждый элемент которого определяется как минимальный элемент соответствующего столбца исходной матрицы А=(аi,j)6,7. Преобразовать исходную матрицу А=(аi,j)5,7 так, чтобы последний элемент каждой строки был заменен суммой предыдущих элементов той же строки. Преобразовать заданную матрицу В=(bi,j)4,6 таким образом, чтобы первый элемент каждого столбца был заменен произведением последующих элементов того же столбца. Преобразовать матрицу С=(сi,j)8,8 так, чтобы все элементы расположенные ниже главной диагонали, были уменьшены вдвое, а элементы, расположенные выше главной диагонали – увеличены вдвое. Определить количество и номера отрицательных элементов в матрице А размерностью 67. Последний по счету отрицательный элемент заменить суммой положительных элементов матрицы. Найти отношение минимального элемента матрицы А=(аi,j)5,6 к максимальному элементу матрицы В=(bi,j)7,8. В заданной матрице А=(аi,j)4,5 найти нулевой элемент с наибольшим значением индекса i и все элементы столбца, в котором находится этот элемент, обнулить. Если в матрице нет нулевых элементов, отпечатать соответствующее сообщение. Найти отношение количества положительных элементов к количеству элементов отрицательных заданной матрицы F. В случае, если матрица F не содержит отрицательных элементов, то все положительные элементы уменьшить на 1. Для квадратной матрицы F=(fi,j)7,7 найти отношение суммы элементов, расположенных ниже главной диагонали, к сумме элементов, расположенных выше главной диагонали, предусмотрев соответствующее сообщение, если последняя сумма (делитель) окажется равной 0. В заданной матрице В=(bij)6,7. Найти элемент bij<5 c наибольшим значением индекса j. Все элементы столбца, в котором находится искомый элемент (кроме него) сделать равными 1. Получить матрицу-строку В, каждый элемент которой равен среднему геометрическому значений элементов соответствующей строки матрицы А размерностью 910. Все элементы матрицы С=(cij)9,9, расположенные выше главной диагонали преобразовать, умножив их на минимальный элемент матрицы С. Задание № 7. Использование процедур и функций Задание. Составить блок-схему алгоритма и программу решения поставленной задачи, которая в соответствии с исходными данными вычисляет значения заданных выражений. Расчет элементов массива и подпрограмму оформить в виде процедур с параметрами. Варианты заданий. 1. Для одномерного массива чисел А1,A2,…Am составить подпрограмму определения значения математического ожидания по формуле: Sl=1.7-3.6∙sin(l/4+0.2), Un=7.8+15.6∙sin(n/2+0.9). 2. Составить подпрограмму подсчета величины процента положительных элементов – Р в одномерном массиве А1,A2,…Am. Использовать подпрограмму для обработки массивов D[70], F[80], R[40], P[30], элементы которых вычисляются по формулам: Di=3.1i2-59.7i-16.2, Fj=5.4j2-82.1j+29.6, Rk=-6.9k2-+31.2k-10.5, Pm=-11.5m2+48.2m+15.6. 3. Составить подпрограмму определения разности g между максимальным и минимальным значениями элементов одномерного массива b1, b2,…bm. Подпрограмму использовать для обработки массивов A[40], D[80], H[50] и Q[70], элементы которых вычисляются по формулам: Ai=-(i-2)2+i3, Dj=1.5(j-3.2)2-1.1j3, Нk=2.7(k-0.2)2-0.5k3, Qn=3.3(n+2.5)2-1.8n3. 4. Составить подпрограмму определения номера строки матрицы A(M,N), в которой находится наибольший по абсолютной величине элемент матрицы. Подпрограмму применить для обработки матриц: X[30,40], Y[50,50], Z[60,40], элементы которых вычисляются по формулам: Xij=5.7∙j∙sin(i/2)+9.3∙i∙cos(j/2), Yij=12.1∙j∙sin(i/2)-3.8∙i∙cos(j/2), Zij=10.5∙j∙sin(i/2)+23.4∙i∙cos(j/2) 5. Составить подпрограмму формирования массива D=[d1,d2,d3,d4], где di – максимальный по модулю элемент соответственно массивов A[140], B[80], C[90], F[70], элементы которых вычисляются по формулам: Ai=9.6i-15.3∙tg(i2-0.5); Bj=11.6j-18.3∙tg(j2+1.5); Ck= -11.2k+10.1∙tg(k2-3.9); Fl=19.6 l-29.4∙tg(l2-3.3). 6. Составить подпрограмму формирования массива S=[S1,S2,S3,S4], где Si – минимальный положительный элемент массива A[12], B[16], C[20], D[8], соответственно. Элементы массивов вычисляются по формулам: Ai=3.8i2-12.4i+5.1, Bi=5.6i2+11.5i-29.3, Ck=18.1k2-6.8k-9.9, Dl=10.5l2-21.6l+6.9. 7. Составить подпрограмму формирования вектора Q=[Q1,Q2,Q3,Q4], компоненты которого равны произведению ненулевых элементов массивов A[9], F[10], Z[6], D[7], элементы которых вычисляются по формулам: Ai=1.2∙ (i-2) ∙sin(i), Fj=5.9∙ (j-5) ∙sin(j), Zk=12.3∙ (k-4) ∙sin(k), Dm=8.6∙ (m-1) ∙sin(m). 8. Составить подпрограмму вычисления скалярных произведений векторов Х и У по формуле Вi=2.8-(i+4.5)2, Ci=-12.6+(i-2.2)2, Zi=-9.1-(i+5.7)2, Si=8.5-(i-2.7)2, где i=1…100. 9. Составить подпрограмму нахождения разности между суммой элементов с четными индексами и суммой элементов с нечетными индексами в массивах C[60], R[80], S[100], U[70], элементы которых вычисляются по формулам: Сi=2.8+5.1∙sin(i/2+0.5), Rj=6.6+4.7∙sin(j/3-1.2), Sl=1.7-3.6∙sin(l/4+0.2), Un=7.8+15.6∙sin(n/2+0.9). 10. Составить подпрограмму нахождения суммы положительных элементов одномерного массива х1,х2,…хn. Подпрограмму использовать для обработки массивов A[90], F[100], Z[60], P[70], элементы которых вычисляются по формулам: Ai=1.2∙ (i-2) ∙sin(i), Fj=5.9∙ (j-5) ∙sin(j), Zk=12.3∙ (k-4) ∙sin(k), Pm=8.6∙ (m-1) ∙sin(m). 11. Составить подпрограмму, которая по исходным массивам C[60], R[80], S[100] формирует вектор Q=[Q1,Q2,Q3], где компоненты Qi равны произведению отрицательных значений элементов массива. Элементы массивов вычислять по формулам: Сi=2.8+5.1∙sin(i/2+0.5), Rj=6.6+4.7∙sin(j/3-1.2), Sl=1.7-3.6∙sin(l/4+0.2). 12. По исходным массивам A[40], D[80], H[50] сформировать массив G=[G1,G2,G3], компоненты которого равны суммам абсолютных значений исходных массивов. Расчет значения суммы оформить в виде отдельной программы. Элементы массивов вычислять по формулам: Ai=-(i-2)2+i3, Dj=1.5(j-3.2)2-1.1j3, Hk=2.7(k-0.2)2-0.5k3. 13. Заданы матрицы Сij, Djm, Smi (где i=1...40, j=1…30, m=1…50). Составить подпрограмму определения суммы элементов k строк каждой матрицы. Значение k задать при вводе. Элементы массивов определять по формулам: Сij=(i-3.5) ∙ (j+1.7), Djm=(j+4.2) ∙ (m-5.6), Smi=(m-7.6) ∙ (i+5.2). 14. Составить подпрограмму для расчета общего количества элементов массивов A[140], B[80], C[90], которые принадлежат отрезку [m;n]. Значения m и n задаются при вводе. Элементы массивов определять по формулам: Ai=9.6i-15.3∙tg(i2-0.5); Bj=11.6j-18.3∙tg(j2+1.5); Ck= -11.2k+10.1∙tg(k2-3.9). 15. Составить подпрограмму, которая по исходным массивам A[20], B[180], C[60], D[30] формирует массив Q=[Q1,Q2,Q3,Q4], компоненты которого равны минимальным по абсолютной величине элементам массивов A,B,C,D. Элементы исходных массивов вычислять по формулам: Ai=14.4i-2.9esin(i), Bj= -8.5j+1.6esin(j); Ck=11.3k-4.7esin(k), Dl=-18.1e+12.9esin(l). 16. Составить подпрограмму для определения суммы элементов квадратной матрицы X[n,n], лежащих на главной диагонали, и использовать ее для обработки матриц А[10,10], В[40,40], С[80,80]. Элементы матриц определяются по формулам: Aij=3.7-8.2ij2+10.4i2j, Bij=-5.2+13.9ij2-4.6i2j, Cij=8.4+4.6ij2-7.5i2j. 17. Cоставить подпрограмму подсчета произведения положительных элементов массива Х и использовать ее для обработки массивов A[12], B[16], C[20], D[8], элементы которых вычислять по формулам: Ai=3.8i2-12.4i+5.1, Bi=5.6i2+11.5i-29.3, Ck=18.1k2-6.8k-9.9, Dl=10.5l2-21.6l+6.9. 18. Составить подпрограмму определения отношения максимального и минимального элемента массива Х(n), с помощью которой рассчитать z=a+b+c, где a,b,c – отношения максимальных и минимальных элементов массивов A[140], B[80], C[90], F[70], рассчитываемых по формулам: Ai=9.6i-15.3∙tg(i2-0.5); Bj=11.6j-18.3∙tg(j2+1.5); Ck= -11.2k+10.1∙tg(k2-3.9); Fl=19.6 l-29.4∙tg(l2-3.3). 19. Заданы массивы A[12], B[16], C[20], D[8]. Составить подпрограмму для нахождения разницы между произведениями элементов с четными индексами и произведениями элементов с нечетными индексами каждого из массивов. Элементы массивов рассчитать по формулам: Ai=3.8i2-12.4i+5.1, Bi=5.6i2+11.5i-29.3, Ck=18.1k2-6.8k-9.9, Dl=10.5l2-21.6l+6.9. 20. Составить подпрограмму определения суммы элементов квадратной матрицы, лежащих выше главной диагонали, которую использовать для обработки матриц X[30,30], Y[50,50], Z[60,60]. Элементы указанных матриц определить по формулам: Xij=5.7∙j∙sin(i/2)+9.3∙i∙cos(j/2), Yij=12.1∙j∙sin(i/2)-3.8∙i∙cos(j/2), Zij=10.5∙j∙sin(i/2)+23.4∙i∙cos(j/2). Рекомендации к выполнению контрольной работыДля выполнения контрольной работы составить блок-схему алгоритма решения задачи и программу на языке программирования Турбо Паскаль в соответствии с выбранным вариантом задания. Номер варианта задания выбирается по буквам фамилии студента в соответствии с таблицей.
Например, для студента с фамилией Сидоров варианты в каждом задании будут такими: 1 задание – 17 вариант (буква С) 2 задание – 9 вариант (буква И) 3 задание – 5 вариант (буква Д) 4 задание – 14 вариант (буква О) 5 задание – 16 вариант (буква Р) 6 задание – 14 вариант (буква О) 7 задание – 3 вариант (буква В) Если фамилия состоит меньше, чем из 7 букв, то в качестве недостающих взять первые буквы имени. МЕТОДИЧЕСКОЕ ПОСОБИЕ«ОСНОВЫ АЛГОРИТМИЗАЦИИ» (для студентов заочной формы обучения) Составители: Павлыш Владимир Николаевич, д.т.н., проф.Ефименко Константин Николаевич, к.т.н., доц.Добровольский Юрий Николаевич, ст. преп.  Подп. в печать 12.11.12 г. Формат 60х84 1/16. Бумага KumLux. Ризографическая печать. Усл. печ. л. 4,65 Усл. кр.-отт. 4,70 Уч.-изд. л. 4,75 Тираж 50 экз. Заказ № 20/10 |

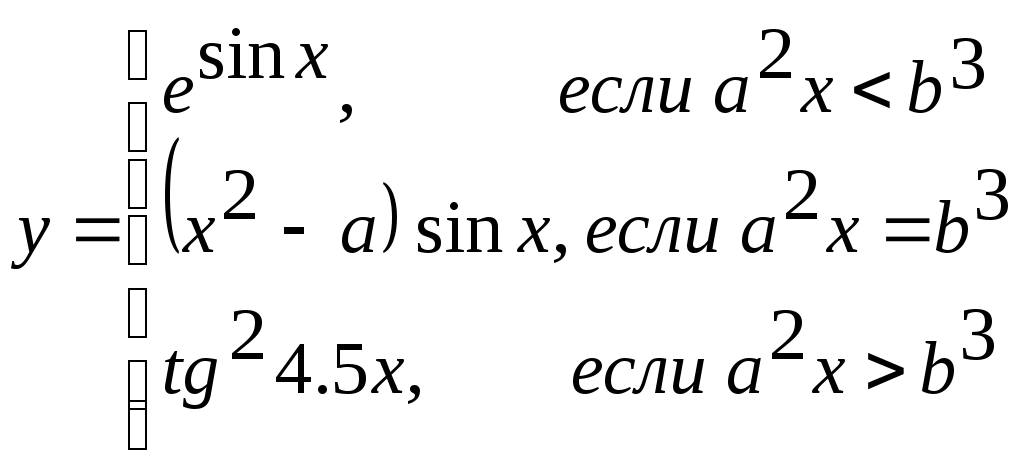
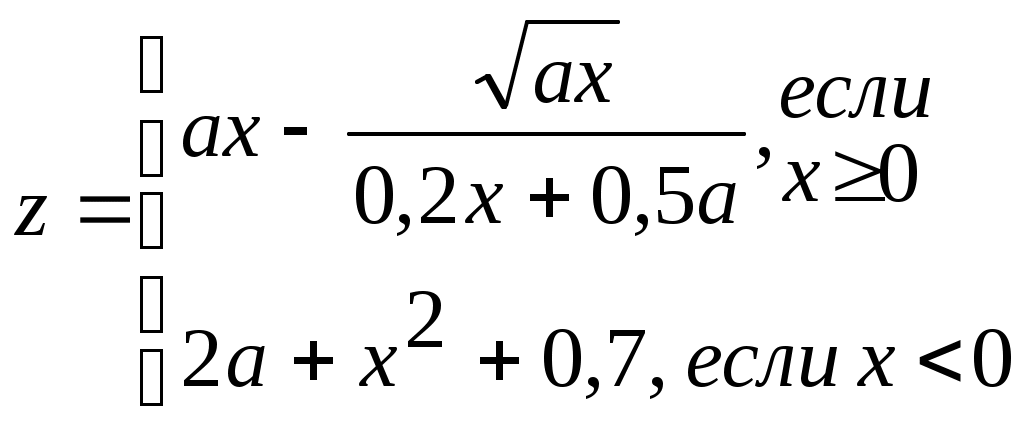
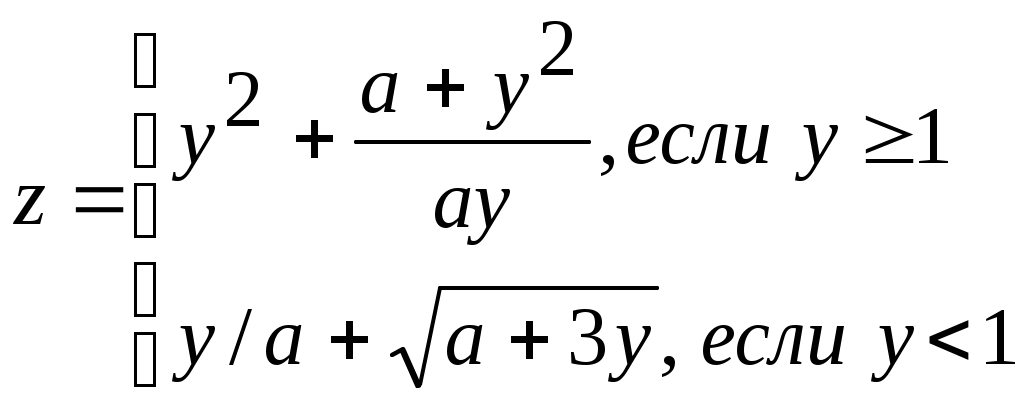
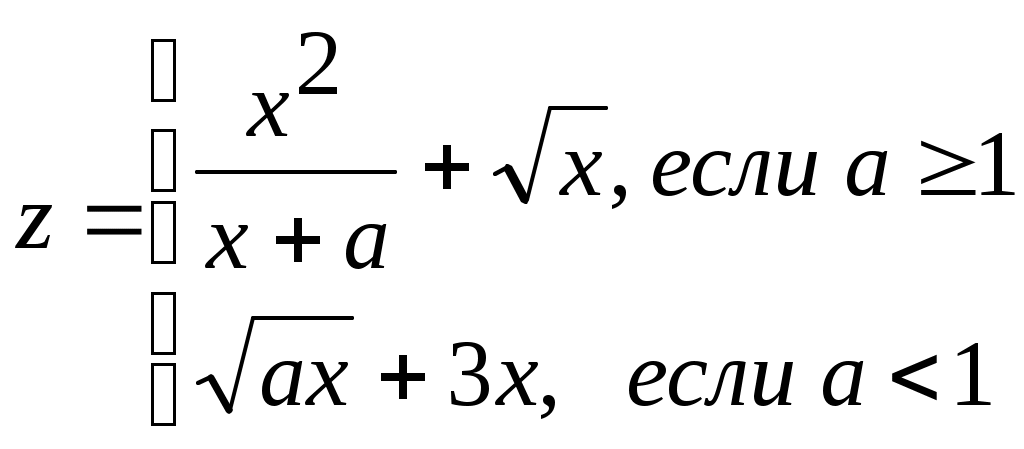
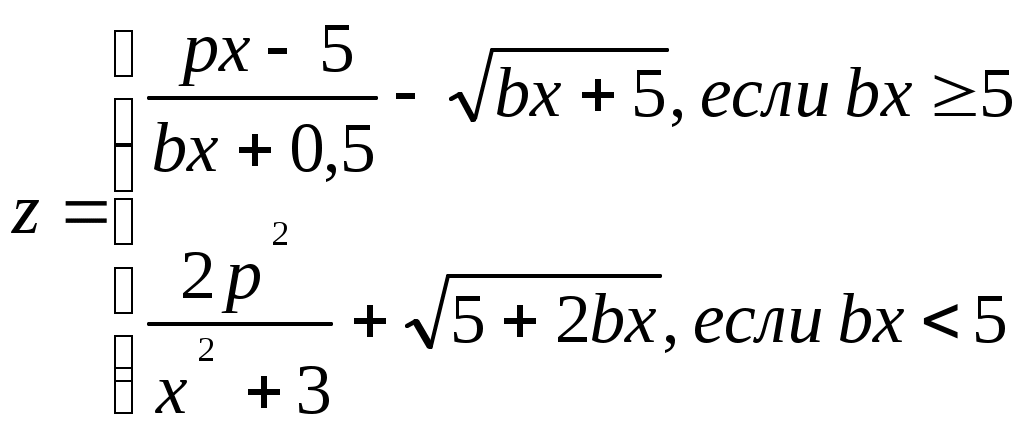
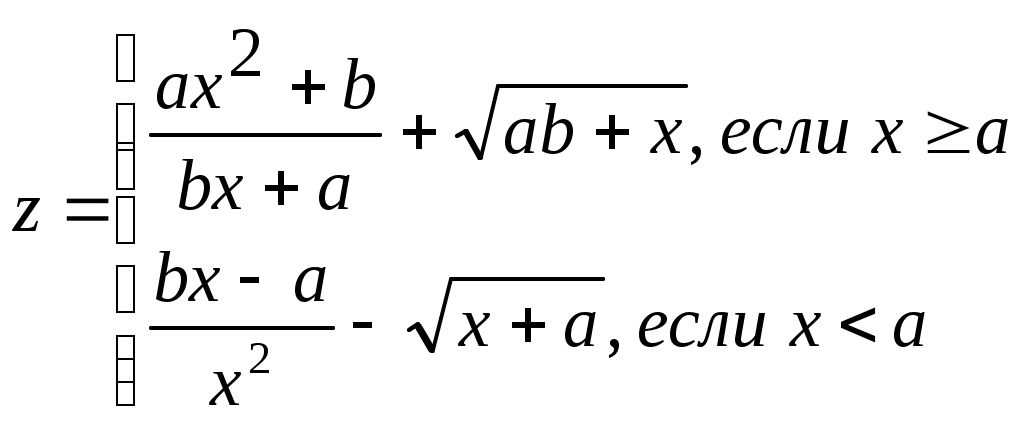
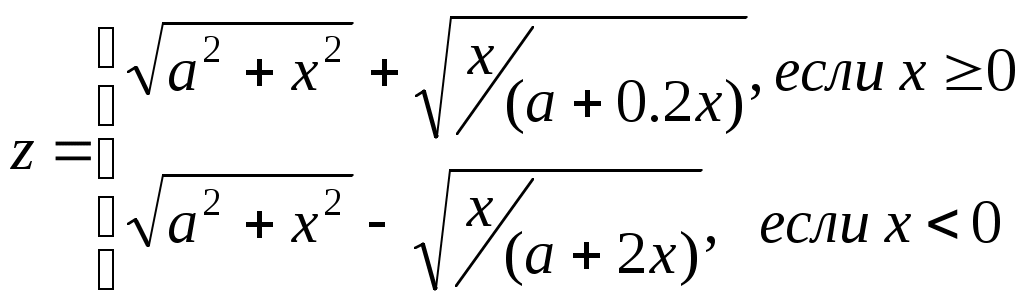
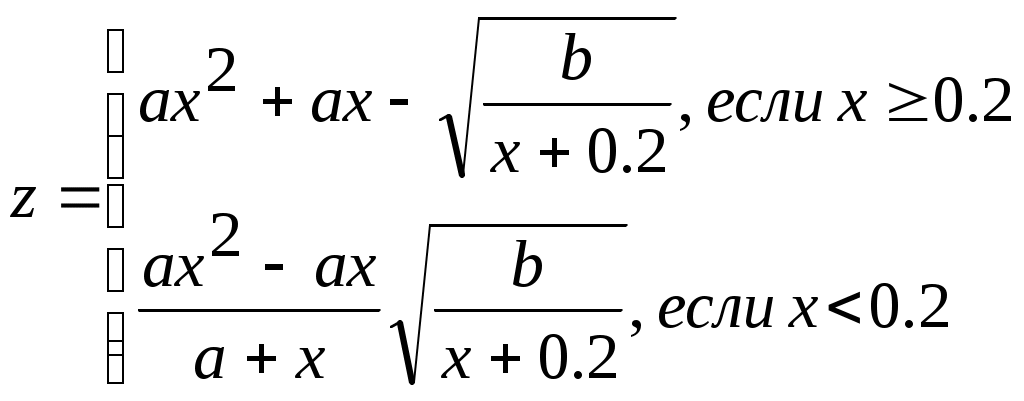
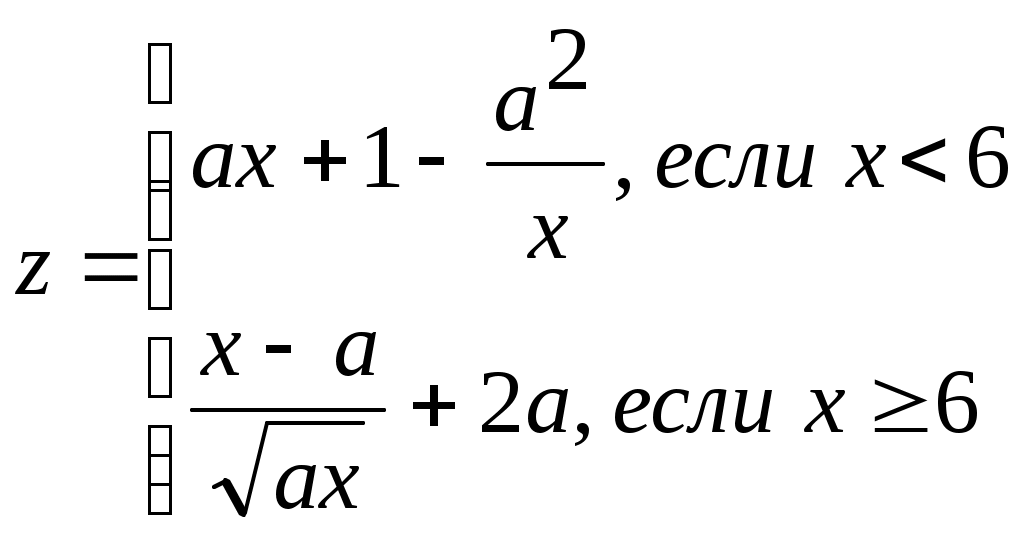
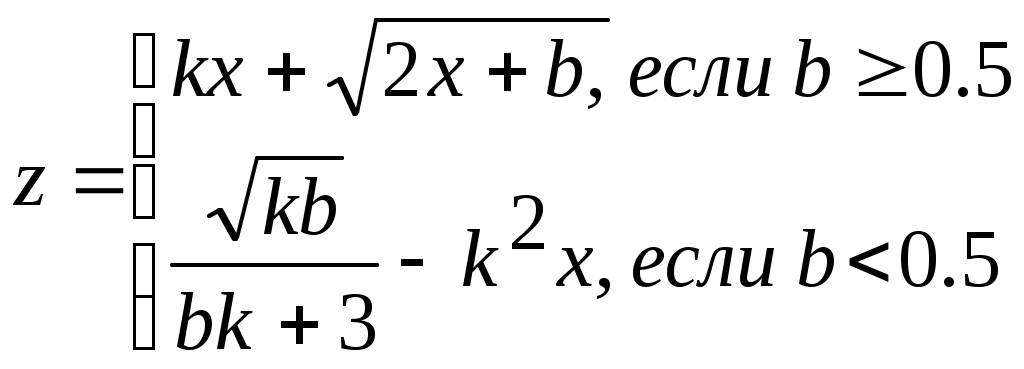
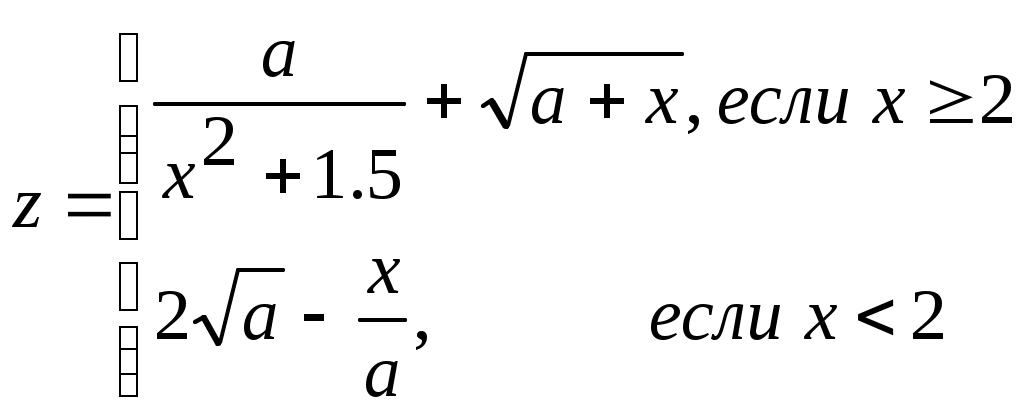
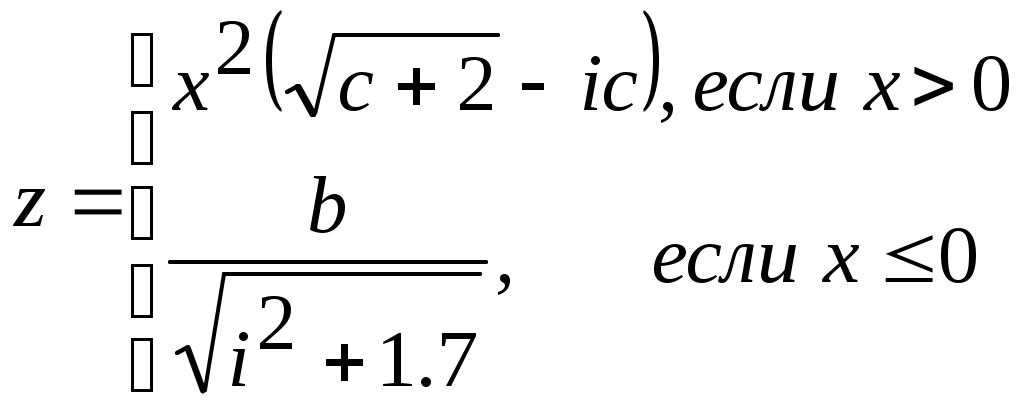
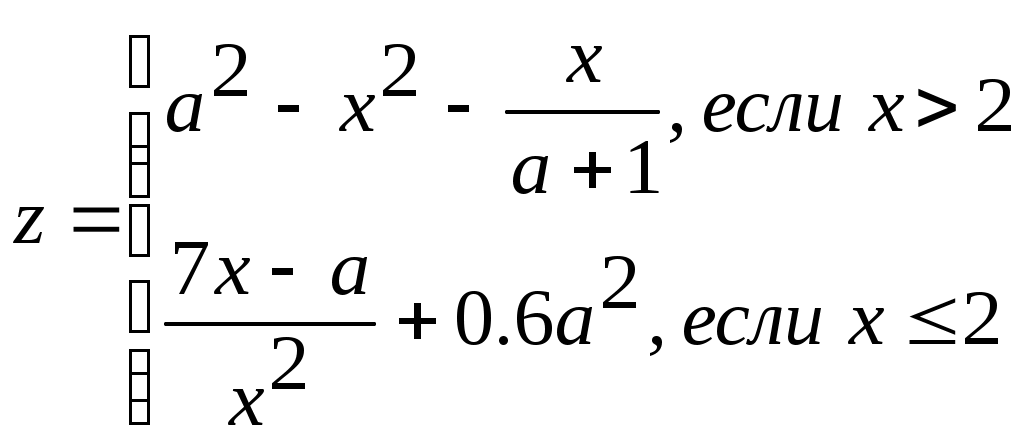
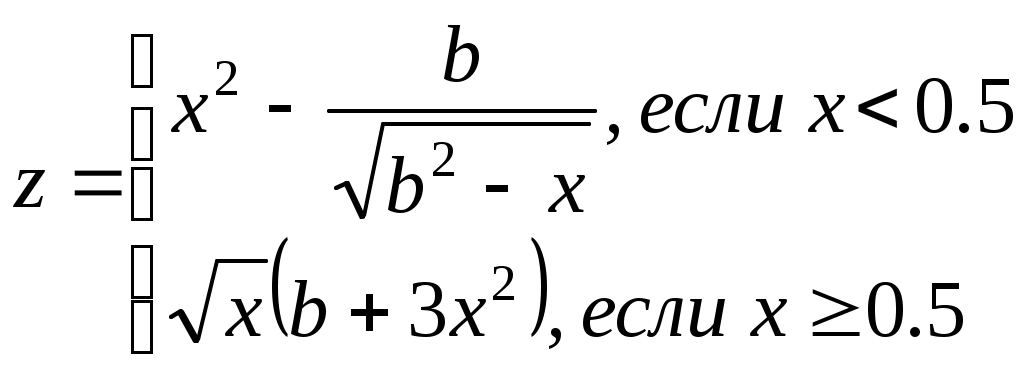
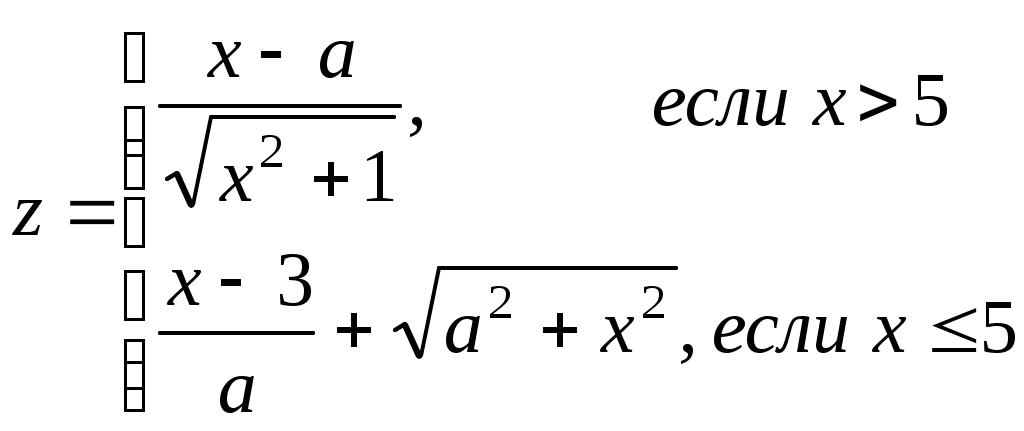
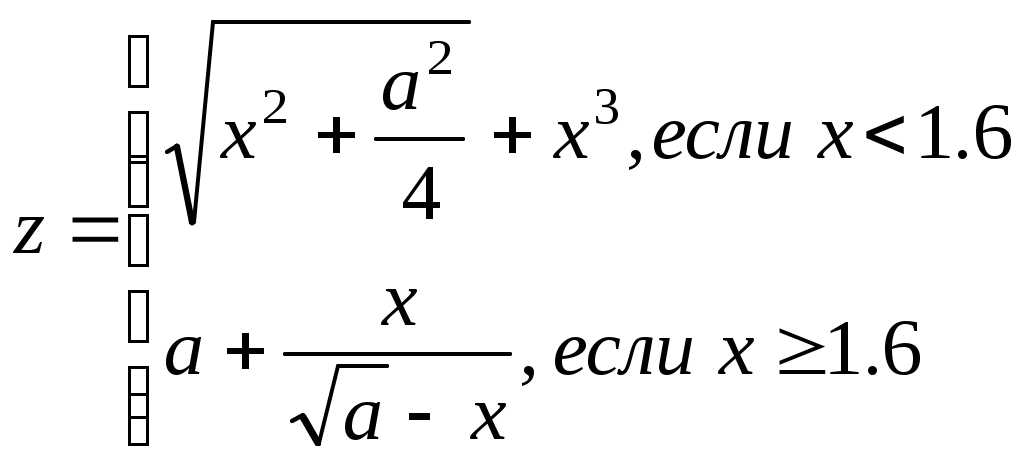
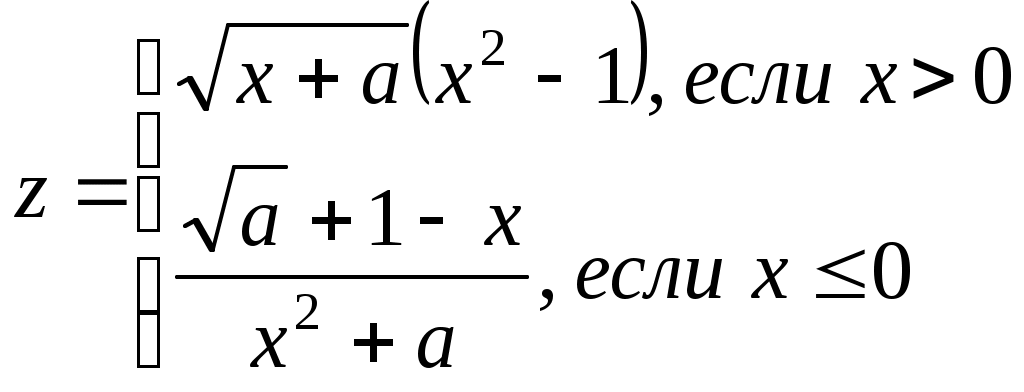
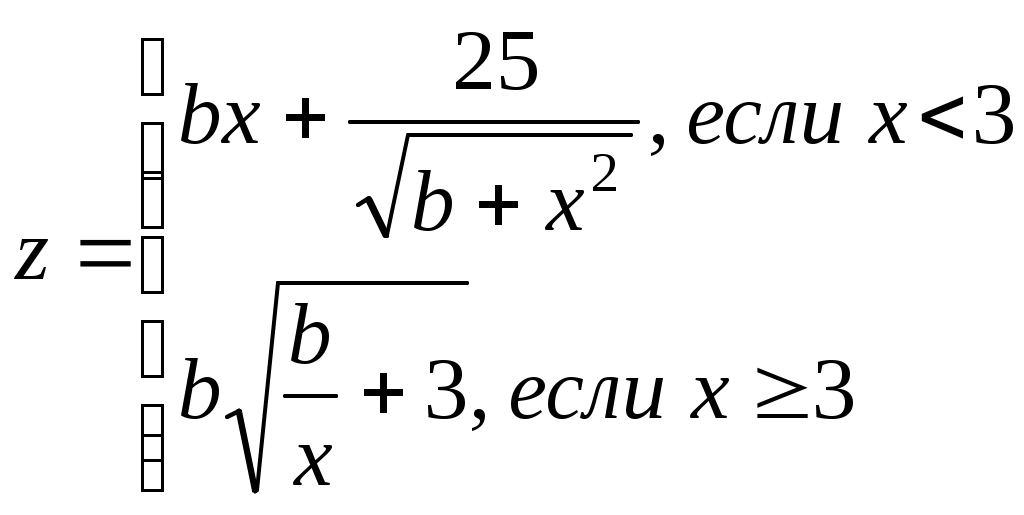
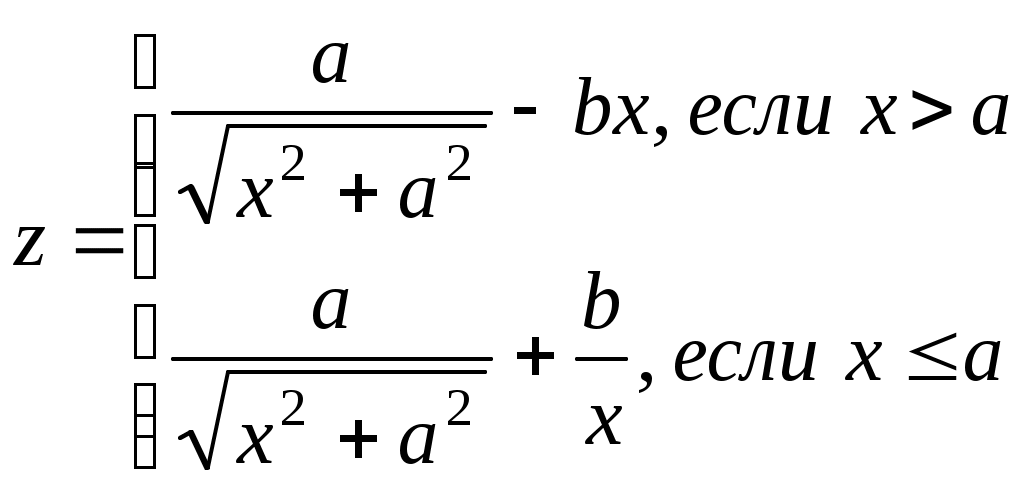
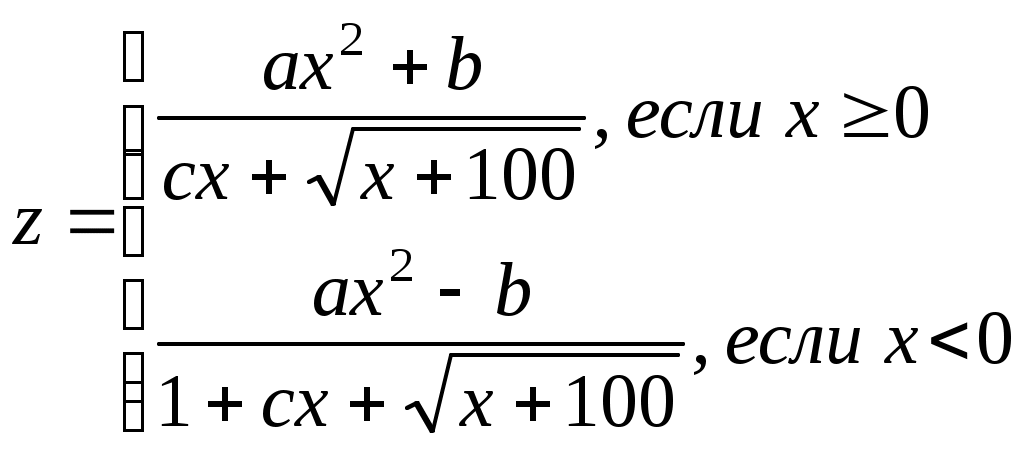 x=(i-a)/i
x=(i-a)/i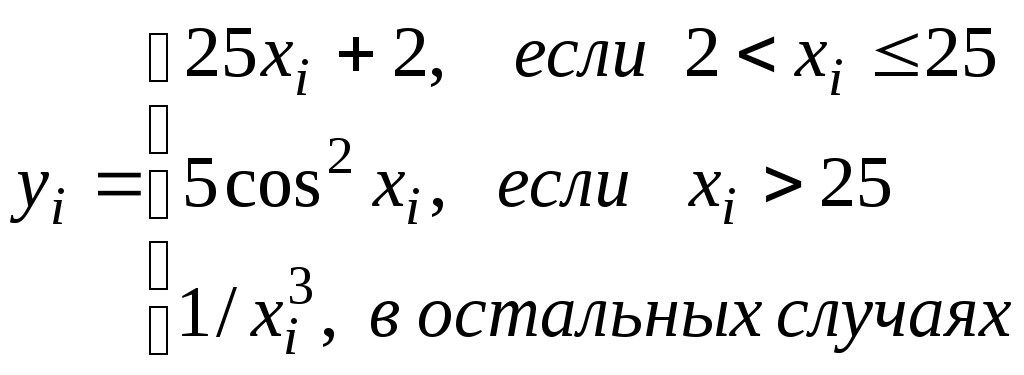
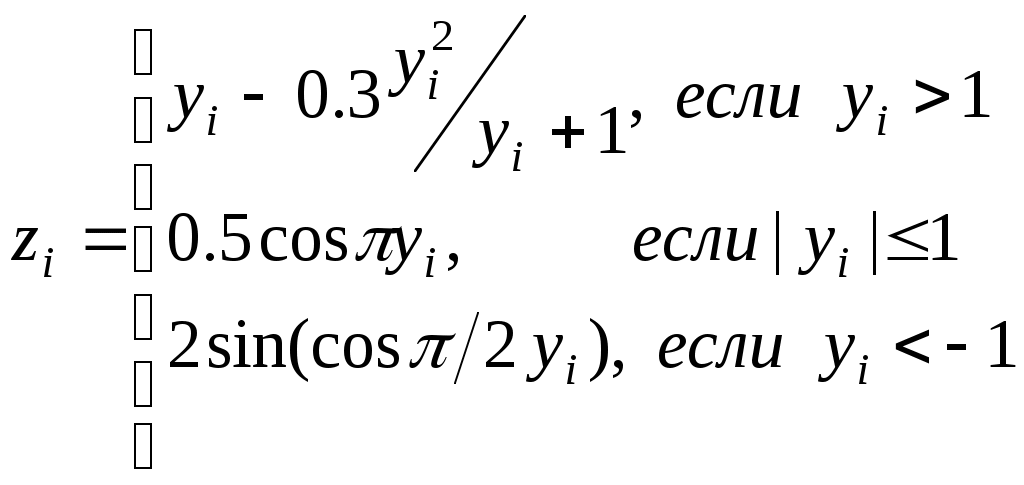
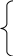 yi=
yi= 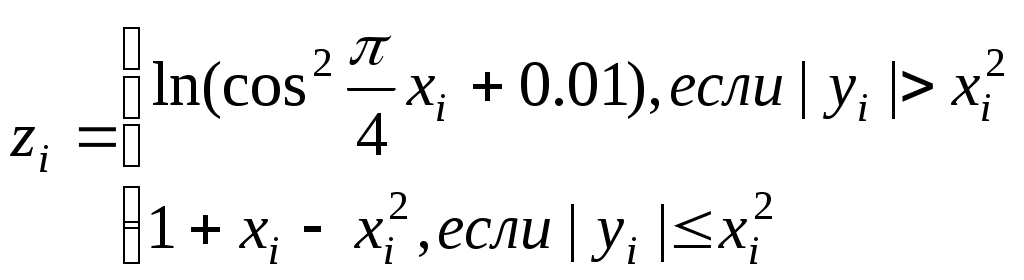
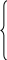
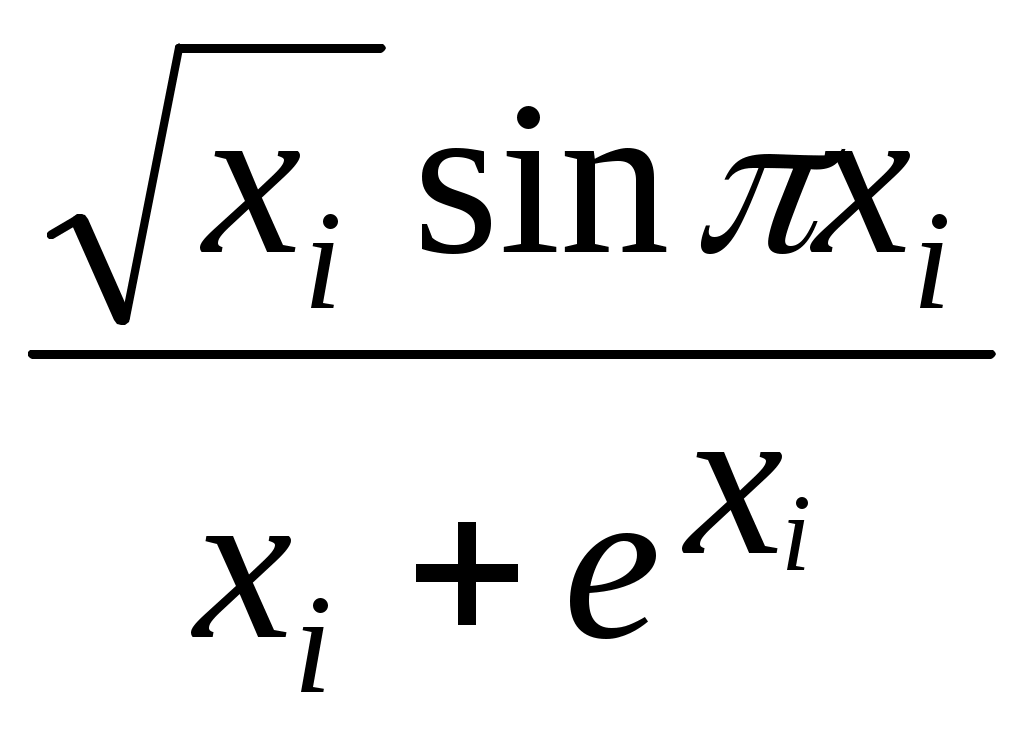 , если xi> 1.5
, если xi> 1.5 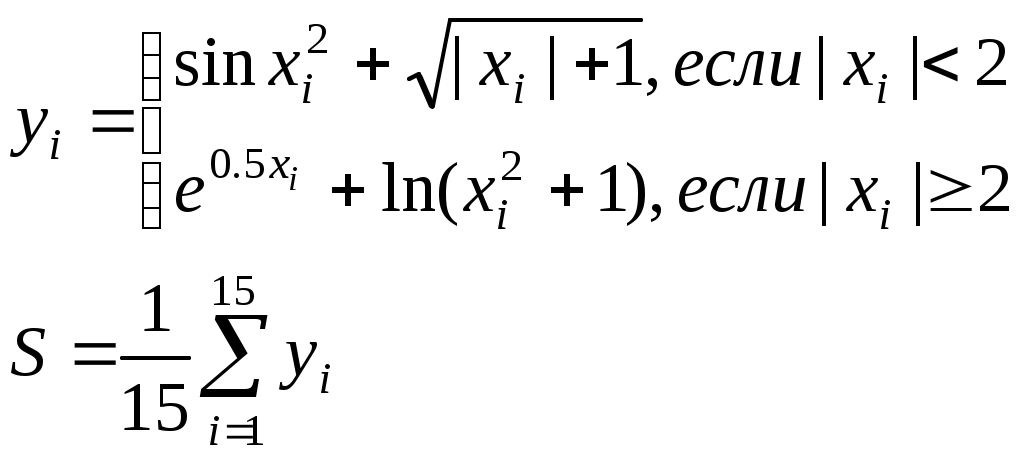
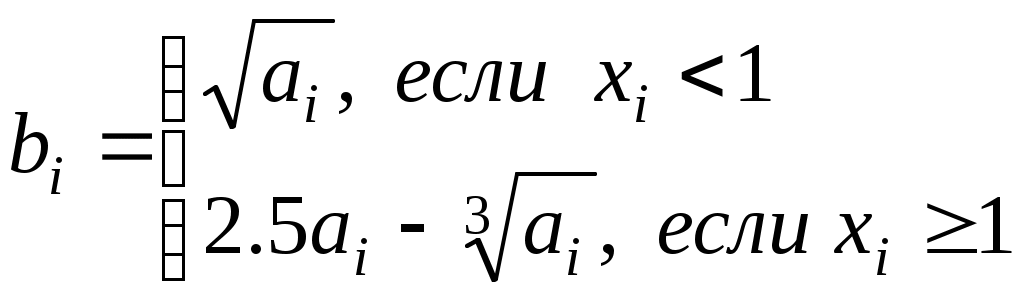
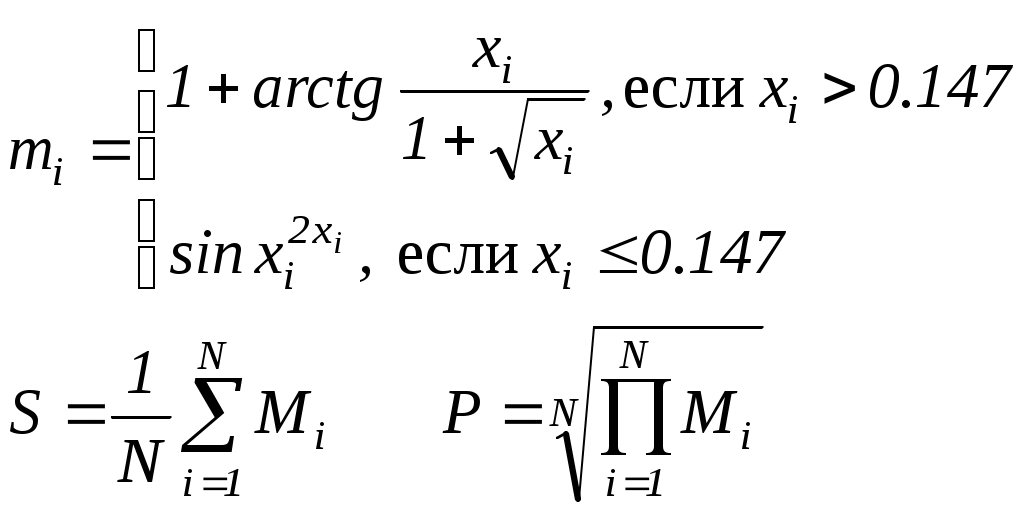
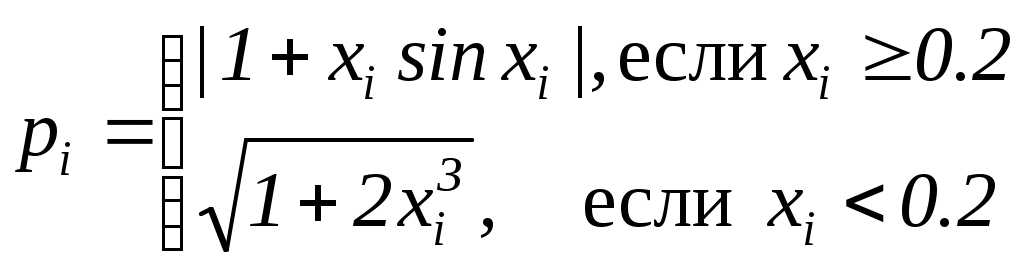
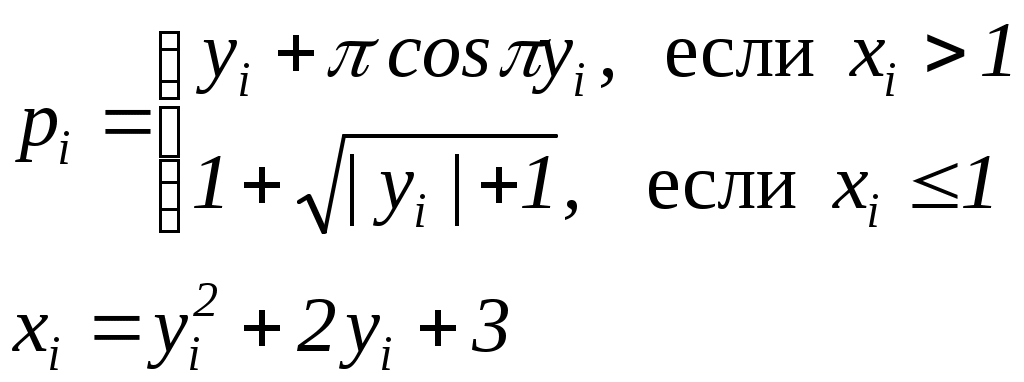
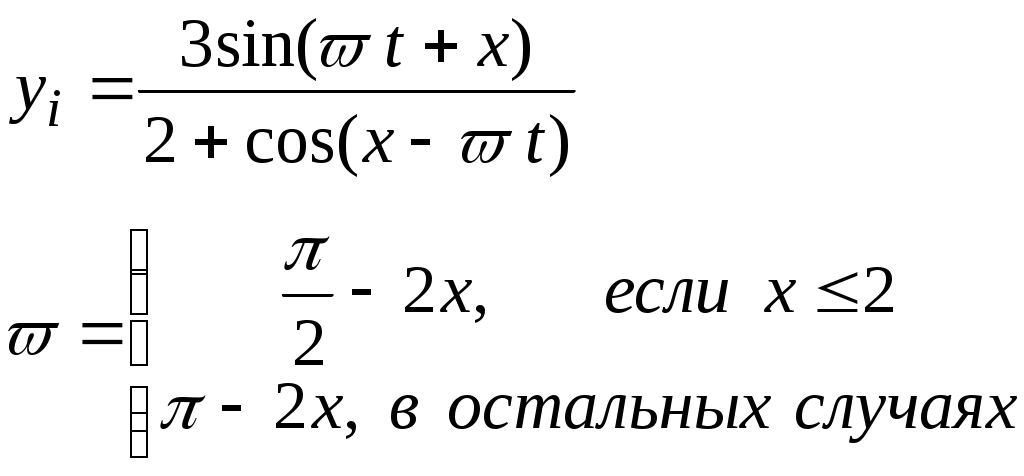
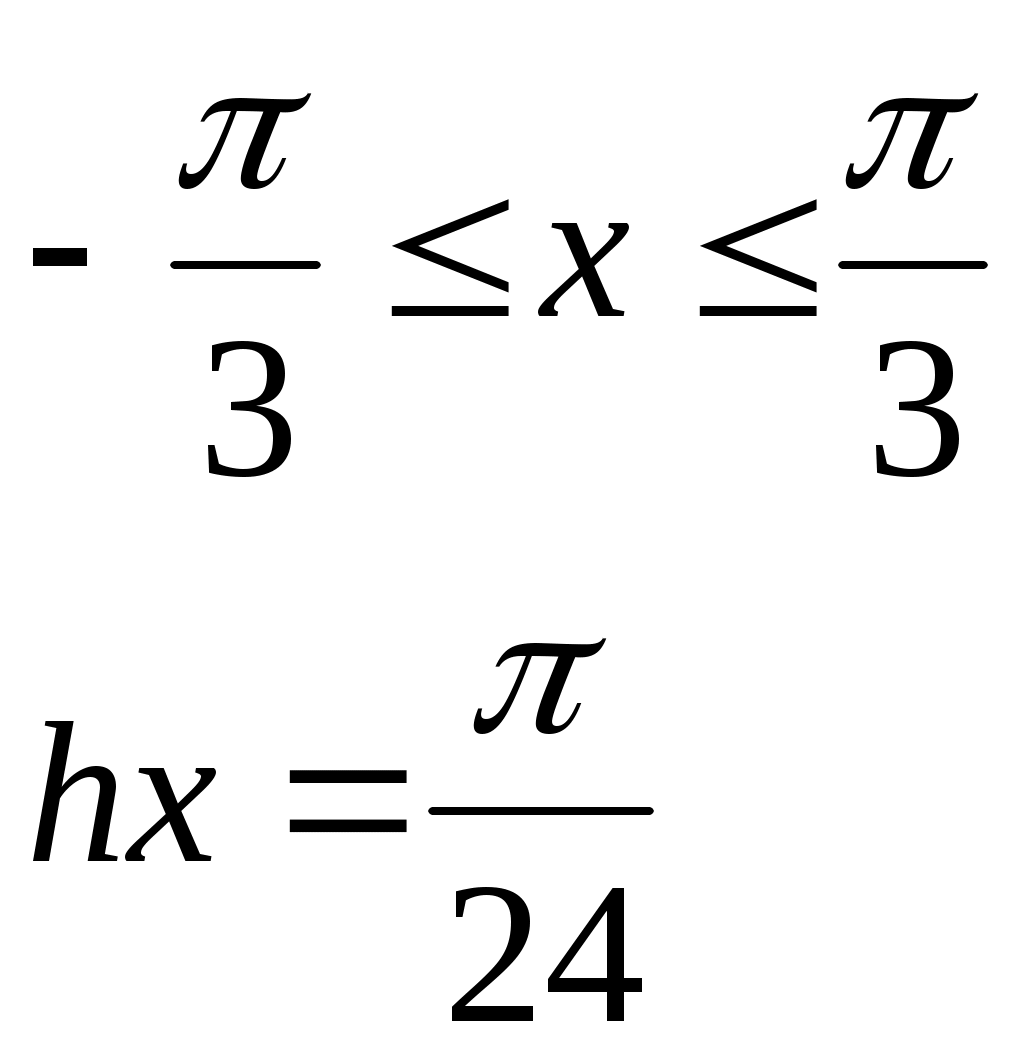
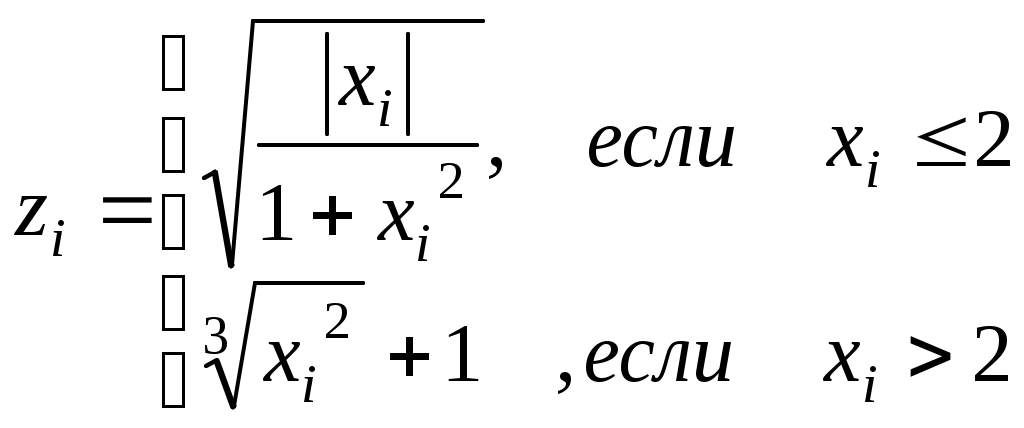
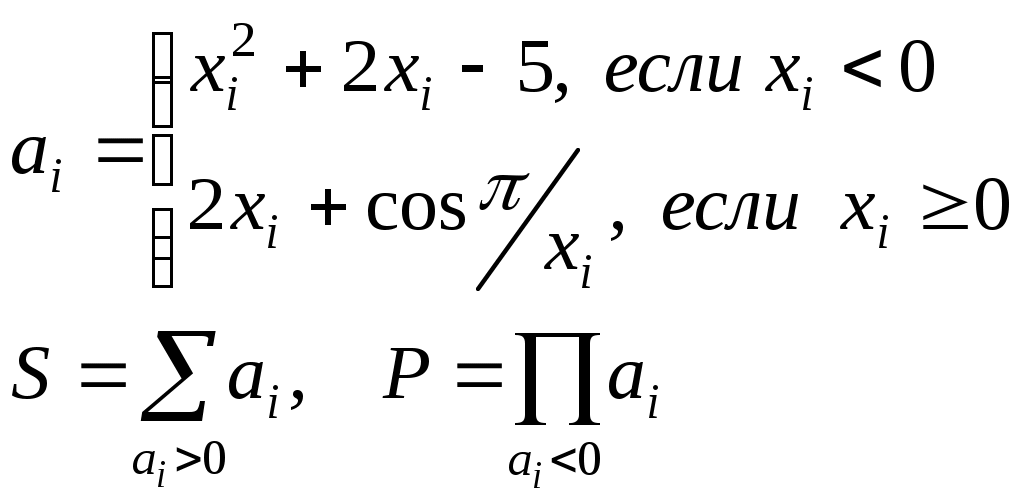
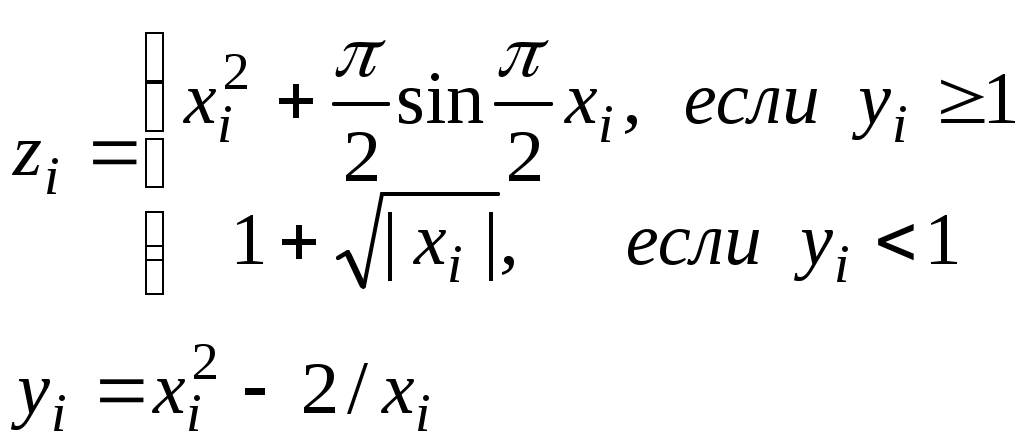
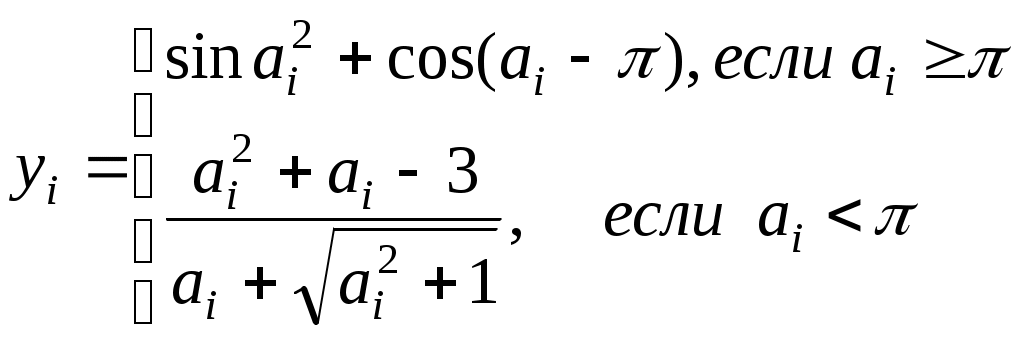
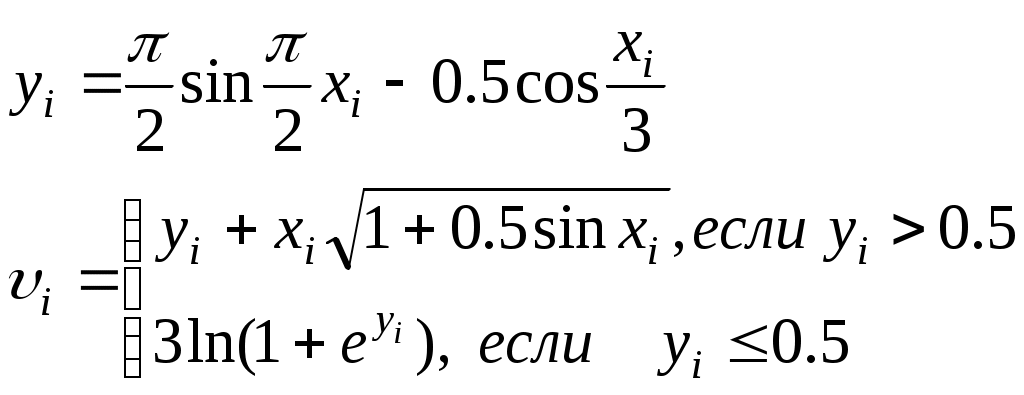 Считать (Vi ,Yi ) координатами точек плоскости. Определить процент (PR) точек, лежащих в круге радиусом R с центром в точке(V0 ,Y0).
Считать (Vi ,Yi ) координатами точек плоскости. Определить процент (PR) точек, лежащих в круге радиусом R с центром в точке(V0 ,Y0).