Работа. Методика решения типовых задач по введению в ЭТ. Методика решения типовых задач микроэкономика

Название	Методика решения типовых задач микроэкономика
Анкор	Работа
Дата	25.06.2022
Размер	51.05 Kb.
Формат файла
Имя файла	Методика решения типовых задач по введению в ЭТ.docx
Тип	Решение #615175

МЕТОДИКА РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

МИКРОЭКОНОМИКА

Екатеринбург

2020

Введение

Решение типовых задач предполагает предварительное изучение студентом соответствующей темы курса. Для этого необходимо прочитать конспект лекций или ознакомиться с курсом лекций в презентациях, размещенных в теоретической части обучающего модуля, учебником.

Каждой типовой задаче предшествует характеристика понятий, категорий, а также формул, которые потребуются в процессе решения типовой задачи.

Решение задачи предполагает осуществление студентом последовательных действий:

Ознакомление с информацией, предшествующей условию задачи.
Изучение условия задачи.
Попытка самостоятельного решения задачи.
Обращение к подробному описанию процесса решения задачи, представленному в данной методике.

Раздел 1. Введение в экономическую теорию

Тема. Кривая производственных возможностей

Для решения задач используются следующие формулы:

Альтернативные издержки производства единицы товара X:

–∆Y/∆X (1)

∆Y – количество товара Y, на которое сокращается его производство, чтобы увеличить производство товара X;

∆X – количество товара X, на которое увеличивается его производство в результате сокращения производства Y.

r_ixX+r_iyY=R_i (2)

r_ix– затраты ресурса i на производство единицы товара X;

r_iy – затраты ресурса i на производство единицы товара Y;

X – объем производства товара X;

Y – объем производства товара Y;

R_i– объем ресурса i.

Задача 1. По приведенным в таблице данным рассчитайте максимальную величину альтернативных издержек, связанных с выпуском автомобилей.

Вид продукции	Альтернативные производственные возможности
Вид продукции	А	B	C	D	E
Автомобили, млн. шт.	0	2	4	6	8
Ткани, млн.м	40	38	32	18	0

Решение. Альтернативные издержки производства автомобилей (товар Х) – это количество ткани (товар Y), от которого нужно отказаться, чтобы произвести дополнительное количество автомобилей. Для решения задачи используется приведенная выше формула 1.

Вид продукции	Альтернативные производственные возможности
Вид продукции	А	B	C	D	E
Автомобили, млн. шт.	0	2	4	6	8
Ткани, млн.м	40	38	32	18	0
Альтернативные издержки (альтернативная стоимость автомобилей)		–(38–40) =1 2–0	–(32–38) =2 4–2	–(18–32) =7 6–4	–(0–18) =9 2–0 Максимум

Ответ: 9 млн. м ткани.

ЗАДАЧА 1

Постановка задачи: На основании таблицы определите альтернативные издержки производства товара В:

Варианты	Товар А	Товар В
1	3000	100
2	2000	200

Технология решения задачи: чтобы произвести 100 единиц товара В надо отказаться от 1000 единиц товара А, эти потери и являются альтернативной издержками производства товаров В. Для увеличения производства единицы товара В альтернативные затраты составят 10 единиц товара А.

Ответ: 10 единиц товара А.

ЗАДАЧА 2

Постановка задачи: Менеджер имеет 4 часа, в течение которых он должен подготовиться к совещанию (на что требуется не меньше 2 часов), встретиться с клиентом (1 час), пообедать (0,5 часа), прочитать новости с финансового рынка (0,5 часа). Неожиданно ему позвонил руководитель предприятия и отправил на производственную выставку, что заняло 1,5 часа. Определите альтернативные издержки.

Технология решения задачи: Альтернативные издержки должны составить 1,5 часа. Менеджер должен отказаться от менее важного. Поскольку отменить встречу с клиентом проблематично, так как она заранее обусловливается, то придется отказаться от обеда, чтения новостей и частично от подготовки к совещанию.

Ответ: 0,5 часа обеда; 0,5 часа чтения новостей; 0,5 часа подготовки к совещанию.

ЗАДАЧА 3

Постановка задачи: Студентка МБИ в течение пяти часов свободного времени запланировала следующие дела (в порядке убывания их значимости):

Подготовка к завтрашней контрольной работе – 1 час;
Уборка квартиры – 1 час;
Подбор материалов к докладу – 1 час;
Покупка продуктов и приготовление пищи – 1 час;
Чтение детектива, взятого в библиотеке, срок возврата которого давно наступил – 1 час.

Чего будет стоить студентке встреча с подругой (1,5 часа).

Технология решения задач: Ради встречи с подругой студентке придется отказаться от чтения детектива и сократить время (на полчаса) на покупку продуктов и приготовления пищи, так как это менее значимые для нее дела, и альтернативные издержки будут при этом наименьшие.

Ответ: 1час чтения детектива и 0,5 часа на покупку продуктов и приготовления пищи.

Задачи на построение кривой производственных возможностей

ЗАДАЧА 4

Постановка задачи: Постройте кривую производственных возможностей, исходя из следующих данных:

Варианты	Товар А	Товар В
1	3000	100
2	2000	300
3	500	500

Определите, где будут находиться точки, соответствующие следующим комбинациям: а) 1500 А + 250 В, б) 2000 А + 350 В, в) 2500 А +200 В.

Технология решения задачи:

Постоим график производственных возможностей , для этого по оси Х отложим количество товара В, а по оси У – количество товара А. Отметим точки, соответствующие комбинациям товаров А и В (точки 1, 2 и 3. Соединив точки, получим кривую, характеризующую возможности производства этих товаров. Теперь отметим точку а), характеризующую следующий набор товаров: 1500 А + 250 В. Данная точка оказалась под кривой трансформации, следовательно при таком производстве часть производственных факторов будет не задействована полностью. Точно также находим точку б). Она лежит выше кривой. Значит на такое производство не достаточно средств. Точка в) лежит на самой кривой трансформации.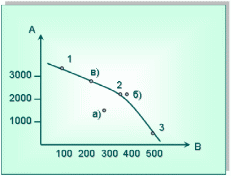

ЗАДАЧА 5

Постановка задачи: Рассмотрите кривую производственных возможностей. Чем отличается точка А от точки В. Где должна находится точка, если мы анализируем современную экономику России?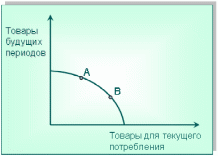

Технология решения задачи: Точка А характеризует выбор в пользу будущего потребления, точка В – в пользу товаров сегодняшнего дня. Потребление в современной России близко к точка А, то есть будущий экономический рост обеспечивается ценой отказа от части текущего потребления, что неверно, так как потребление и так находится на низком уровне. Чтобы обеспечить более быстрый экономический рост в будущем, необходимо стимулировать производителей в настоящее время расширять производство. Для этого необходимо увеличить потребление, то есть переместиться в точку, близкую В.

ЗАДАЧА 6

Постановка задачи: Постройте кривую трансформации. Рассмотрите факторы, которые могли сместить кривую производственных возможностей вправо?

Технология решения задачи: Постоим график производственных возможностей, для этого по оси Х отложим количество товара У, а по оси У – количество товара Х. Возьмем произвольные точки и проведем через них кривую, характеризующую возможности производства этих товаров. Параллельно ей проведем еще одну кривую (на графике отмечена пунктиром). Смещение кривой вправо возможно вследствие следующих факторов: внедрения достижений научно-технического прогресса, увеличения ресурсов в производстве этих товаров, роста качества факторов производства, роста капитала, роста производительности труда и т. п.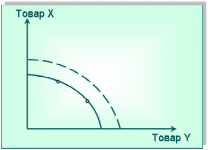

Раздел 2. Микроэкономика

Тема. Основы теории спроса и предложения

Задача 1. Спрос на товар описывается уравнением: Qd=10-p. В результате роста доходов спрос на товар вырос для каждого уровня цены на 5 ед. Как изменится спрос при цене в 10 ед.?

Решение. Поскольку в результате роста дохода спрос увеличился на 5 ед. для каждого уровня цены, то необходимо определить новый вид функции спроса:

Qd=10-p+5=15-p

Объем спроса при цене в 10 ед. (до увеличения дохода)

Qd=10-p=10-10=0

Спрос при этой цене отсутствовал. Это была цена «бойкота».

После изменения дохода спрос при цене 10 ед. Qd=15-p=15–10=5

Ответ: спрос изменился на 5 ед.

Задача 2. Функция предложения товара имеет вид: Qs=-5+2p. Государство ввело налог на производителя в размере 3 ед. Каким будет объем предложения при цене 6 ед.? Каким был объем предложения до введения налога при этой цене?

Решение. Новый вид функции предложения с учетом введения налога:

Qs=-5+2(p-t), t – налог равен 3.

Qs=-5+2(p-3)

При цене 6 ед. объем предложения равен 1.

Qs=-5+2(6-3) =1

До введения налога объем предложения составлял при цене 6 ед.

Qs=-5+2х6=7

Ответ: При цене 6 ед. объем предложения равен 1. До введения налога объем предложения составлял 7 ед.

Тема. Эластичность спроса и предложения

Задача 1. Цена товара выросла с 4,5 до 6 ден.ед. Объем спроса на товар сократился с 3000 до 300 штук. Чему равен коэффициент прямой эластичности?

Решение. Для решения задачи используется формула центральной точки

Ed_х=(Pср./Qср.)х(∆Q /∆P)

(6+4,5)/2 х 300-3000

(3000+300)/2 6-4,5

Ответ: 5,7

Задача 2. Функция спроса на товар Х имеет вид: Qdх=50-4Pх+0,8 Py. Цена товара Х равна 5 ден.ед., цена товара Y равна 10 ден.ед. Определите коэффициенты прямой и перекрестной эластичности товара Х.

Решение. Объем спроса на товар Х при данных ценах:

Qdх=50-4х5+0,8 х10=38

Для решения задачи используется формула точечной эластичности

Eхpх=(Pх/Qdх)х (∆Qdх/∆Pх)

Eхpy =(Py/Qdх)х (∆Qdх/∆Py)

Из формулы Qdх=50-4Pх+0,8 Py

∆Qdх/∆Pх=4 Eхpх=(5/38)х(-4)=0,53

∆Qdх/∆Py=0,8 Eхpy=(10/38)х0,8=0,21

Ответ: Eхpх=0,53, Eхpy=0,21.

Тема. Теория производства и издержек

Задача 1. В таблице представлена зависимость объема выпуска продукции от числа занятых рабочих (прочие факторы производства фиксированы). Определите предельные продукты последовательно нанятых рабочих.

Число рабочих (L)	Валовой продукт (TP)
0	0
1	100
2	200
3	272
4	320
5	350
6	380

Решение. Для решения задачи используются формулы, показывающие связь валового и предельного продуктов:

MP=∆TP/∆L, если ∆L=1, то MP=∆TP.

MP_n= TP_n– TP_n_–1, где n – число работников и номер работника.

Число рабочих (L)	Валовой продукт (TP)	Предельный продукт (MP)
0	0	-
1	100	100
2	200	100
3	272	72
4	320	48
5	350	30
6	380	30

Тема. Экономическое поведение фирмы в условиях совершенной конкуренции и несовершенной конкуренции
Решение задач основано на использовании следующих формул:

Общий, или валовой, доход ТR – денежная сумма, поступающая от продажи всего объема продукции. Рассчитывается как произведение цены на количество единиц: TR=PQ (1)

Средний доход АR – выручка, полученная от продажи единицы продукции: AR= TR/Q=P (2)

Предельный доход МR – добавочный доход, полученный от продажи дополнительной единицы продукции, т.е. приращение дохода в результате реализации каждой последующей единицы продукции: MR=∆TR/∆Q (3)

Фирма максимизирует валовую прибыль, если MR=MC.

Валовая прибыль – это разница между валовым доходом и валовыми издержками: Tπ =TR–TC (4). Средняя прибыль – это прибыль, полученная от продажи единицы продукции:ATπ = Tπ/ Q=AR–ATC
Задача 1.Спрос на продукцию конкурентной отрасли Q_d=110–2p, а предложение Q_s=4p–10. Восходящий отрезок кривой предельных издержек фирмы описывается уравнением МС=6Q–10. При какой цене и каком объеме производства фирма максимизирует прибыль?

Решение. Фирма максимизирует валовую прибыль при объеме производства, при котором MR=MC.

Для совершенно конкурентной фирмы MR=p_e=MC.

Для определения p_e приравниваем Q_d и Q_s. Q_d=110–2p=Q_s=4p–10. Отсюда p_e=20.

Далее p_e= 20=MR= MC=6Q–10, т.е. 6Q–10=20, Q=5.

Ответ: Q=5, p=20.
Индекс рыночной концентрации Херфиндаля-Хиршмана

Этот индекс определяется путем суммирования квадратов процентной доли рынка каждой из фирм отрасли. Так, если в отрасли имеется n различных фирм, то формула имеет следующий вид:

H = p₁² + p₂² +p₃² +…+ p_n², где Н - индекс рыночной концентрации Херфиндаля-Хиршмана; р - доля рынка каждой из фирм отрасли в процентах; n - количество фирм в отрасли.
Задача 1. В отрасли функционируют 5 фирм, производящих следующие объемы продукции (в %): А – 5%, B – 10%, C – 15%, D – 20%, Е – 50%. Антимонопольный комитет принял решение о разделении фирмы Е на несколько самостоятельных предприятий. На какое количество (n) одинаковых по объемам выпуска продукции предприятий необходимо разделить фирму Е, чтобы индекс Герфиндаля не превышал 1800?

Решение. Обозначим количество фирм, на которое будет разделена фирма Е, через n. Формула индекса Герфиндаля примет вид:

H = p₁² + p₂² +p₃² +…+ p_n²=5²+10²+15²+20²+ n(50/n)²=1800. Отсюда n приблизительно равно 3.

Ответ: n=3.