14 вариант. Министерство науки и высшего образования рф (филиал) федерального государственного автономного образовательного учреждения высшего образования
 Скачать 299.67 Kb. Скачать 299.67 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ (филиал) федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский технологический университет «МИСиС» в г. Губкине Белгородской области Кафедра Горного дела Специальность 21.05.04 Горное дело Специализация Электрификация и автоматизация горного производства Дисциплина Гидравлика КУРСОВАЯ РАБОТА Тема: Гидравлический расчёт сложного трубопровода Студент Кочкин М.В. Группа ГД-ЭиА-19-2з Руководитель работы Доцент Терехин Е.П. Отчет защищен с оценкой__________________________ Комиссия:________________________________________ (подпись, ученая степень, звание, Ф.И.О. ) _________________________________________________ ________________________________________________ «____» __________________ 20____г. Губкин – 2021 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ (филиал) федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский технологический университет «МИСиС» в г. Губкине Белгородской области Кафедра Горного дела Специальность 21.05.04 Горное дело Специализация Электрификация и автоматизация горного производства Дисциплина Гидравлика ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Ф.И.О (группа) вариант
(утверждена на заседании кафедры от ___________ протокол № ______)
Основные вопросы, подлежащие разработке
(подпись, дата) (инициалы, фамилия) Содержани ЗАДАНИЕ 4 Введение 4 1Теоретическая часть 5 1.1Уравнение Бернулли 5 1.2Расчет гидравлических сопротивлений 6 1.2.1Режимы движения жидкости 6 1.3Гидравлические сопротивления по длине 7 1.3.1Ламинарный режим. 7 1.3.2Турбулентный режим 7 2Расчетная часть 9 2.1Задание 9 2.2Решение 11 3Графическая часть 19 Заключение 23 4Использованная литература 24 ВведениеОдной из основных задач гидромеханики и газовой динамики является расчёт гидравлических сопротивлений, возникающих при течении жидкости или газа в проточных каналах газовых и жидкостных машин и аппаратов: реактивных двигателей самолётов и ракет, газовых, паровых и водяных турбин электростанций, центробежных и осевых компрессоров, впускных и выпускных систем поршневых двигателей внутреннего сгорания, в теплообменных аппаратах и т.д. Теоретическая частьУравнение БернуллиРассмотрим установившееся движение идеальной жидкости, находящейся под воздействием только лишь одной массовой силы – силы тяжести. Возьмем одну из струек, составляющих поток, и выделим два произвольных сечения 1–1, 2–2, для которых справедливо уравнение 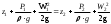 (1) (1)где z – геометрическая высота или геометрический напор; P/(ρg) – пьезометрическая высота или пьезометрический напор; W2/(2g) – скоростная высота или скоростной напор. Уравнение (1) называется уравнением Бернулли для струйки идеальной несжимаемой жидкости. Слагаемые уравнения (1) имеют энергетический, смысл: z – удельная потенциальная энергия положения сечения, P/(ρg) – удельная потенциальная энергия давления движущейся жидкости; (z + P/(ρg)) – полная удельная потенциальная энергия жидкости; W2/(2g) – удельная кинетическая энергия жидкости; Н = z + P/(ρg) + W2/(2g) – полная удельная энергия движущейся жидкости. Вывод: Полная удельная энергия идеальной жидкости элементарной струйки остается постоянной вдоль струйки. Относительно двух сечений потока вязкой жидкости и с учетом отмеченного выше уравнения (1) уравнение энергии для потока примет вид: 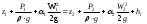 (2) (2) hп – потеря напора (удельной энергии) между сечениями 1–1 и 2–2 потока; α – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей Расчет гидравлических сопротивленийРежимы движения жидкостиВозможны два различных по своему характеру режима движения жидкости: ламинарный и турбулентный. При ламинарном режиме жидкость движется слоями без поперечного перемешивания, причем пульсация скорости и давления отсутствуют. При турбулентном режиме слоистость нарушается, движение жидкости сопровождается перемешиванием и пульсациями скорости и давления. Критерием для определения режима движения является безразмерное число Рейнольдса (Re). Для труб круглого сечения число Рейнольдса определяется по формуле 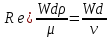 , (3) , (3)где W – средняя скорость жидкости; d – диаметр трубы; ν – кинематическая вязкость жидкости. Режим будет ламинарным, если Re ≤ Reкр, и турбулентным, если Re > Reкр. Для круглых труб обычно принимают Reкр = 2320, и Reкр = 580 для некруглых. Согласно уравнению (2) hп представляет общие потери напора, которые складываются из потерь по длине hдл и местных потерь hм. 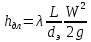 , (4) , (4)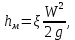 (5) (5)где L, d – длина и диаметр трубопровода; W2 / 2g – скоростной напор; λ – коэффициент гидравлического сопротивления трения, который зависит от режима движения и шероховатости стенок трубы; ζ – коэффициент местного сопротивления, который определяется режимом движения жидкости и видом местного сопротивления в сечении (изменение сечения, трубопроводная арматура и т. п.) Гидравлические сопротивления по длинеОсновной расчетной формулой для определения потерь напора по длине в круглых трубах является универсальная формула Дарси – Вейсбаха (4). Формула применима для ламинарного и турбулентного течения; различие заключается лишь в значениях коэффициента λ. Ламинарный режим.В круглых трубах коэффициент сопротивления λ зависит только от числа Рейнольдса: λ = 64 / Re. (6) Подставляя (3) в формулу получим зависимость, называемую формулой Пуазейля – Гегена: 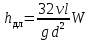 (7) (7)W – средняя скорость жидкости L, d – длина и диаметр трубопровода ν – кинематическая вязкость жидкости. Из этой формулы следует, что потери по длине при ламинарном режиме пропорциональны скорости движения в первой степени и не зависят от состояния внутренней поверхности стенок трубы. Турбулентный режимВвиду сложности турбулентного течения и трудностей его аналитического исследования в большинстве случаев для практических расчетов, пользуются экспериментальными данными. Для количественной оценки шероховатости введено понятие абсолютнойшероховатости Δ, равной средней высоте выступов шероховатости и измеряемой в линейных единицах. При одной и той же абсолютной шероховатости её влияние на гидравлическое сопротивление и распределение скоростей различно в зависимости от диаметра трубы, поэтому введено понятие относительной шероховатостиΔ / d (безразмерная величина). При турбулентном режиме движения коэффициент λ зависит не только от числа Re, но и от Δ / d. При переходе от ламинарного движения к турбулентному слоистое (ламинарное) движение сохраняется у стенок трубы, образуя пристенный ламинарный слой толщиной δл. Беспорядочное движение в середине трубы, где максимальные скорости, образует турбулентное ядро. По мере развития турбулентности ядро увеличивается, а ламинарный слой уменьшается. При δл > Δ трубу называют гидравлически гладкой. В этом случае шероховатость не влияет на движение жидкости. Если δл < Δ, то трубу называют гидравлическишероховатой, и шероховатость существенно влияет на движение жидкости. Сопротивления при движении жидкости: Гидравлически гладких труб; λ = f (Re). Безразмерный комплекс 1) при 4000 < Re <105 – формулой Блазиуса: 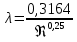 2) при 4000 < Re <3·106 – формулой Конакова: 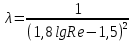 Расчетная частьЗаданиеОпределить массовые расходы в параллельных ветвях трубопровода G1, G2и мощность насоса, если задан суммарный массовый расход жидкости G0и известны конструктивные характеристики элементов трубопровода Определить массовые расходы в параллельных ветвях трубопровода G1, G2и мощность насоса, если задан суммарный массовый расход жидкости G0и известны конструктивные характеристики элементов трубопровода . Сжимаемостью газа пренебречь. Жидкость (газ) подаётся насосом при постоянной температуре и начальном давлении р. Потерями на линии от насоса до разветвления и в самом разветвлении пренебречь. Таблица 1 – Конструктивные и режимные характеристики элементов сложного трубопровода
Конструктивные размеры простого трубопровода
Продолжение таблицы 2
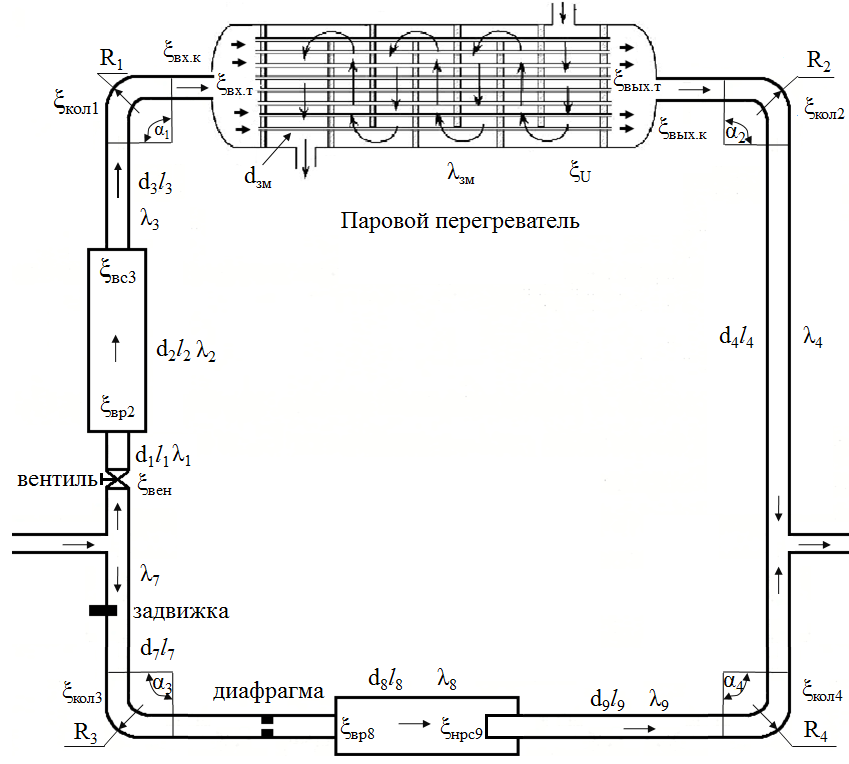 РешениеРасчёт суммарных потерь давления (предполагаем квадратичный закон сопротивления) Потери давления для первой ветви запишутся следующим образом 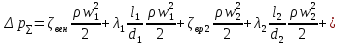 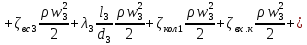 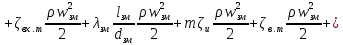 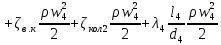 Выразим скорости через массовый расход в 1–й ветви: 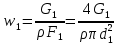 ; ; 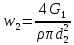 ; ; 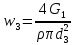 ; ;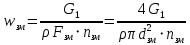 ; ; 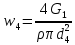 где Fi = πdi2 / 4 – площадь поперечного сечения i–гo участка трубы; Fзм = πdзм2 / 4 – площадь поперечного сечения одной трубки змеевика. Подставляя выражения для скоростей в уравнение и, вынося за скобки общие сомножители, получим 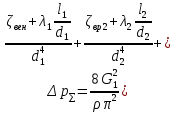 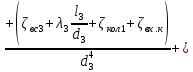 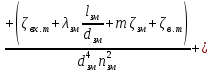 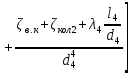 Потери давления для второй ветви 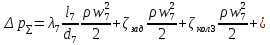 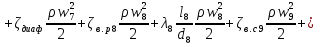 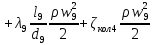 Выразим скорости через массовый расход во 2–ой ветви: 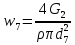 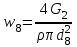 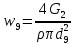 и подставляем в уравнение, тогда 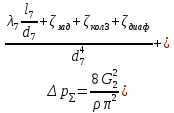 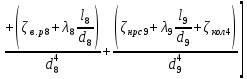 В первом приближении считаем, что λi и ζi , не зависит от числа Re. Тогда значение коэффициентов гидравлического трения определится по формуле Шифринсона λ = 0,11(Δ/dэ)0,25 По таблице для старых бесшовных стальных труб выбираем значение эквивалентной шероховатости Δ = 1,0 мм, а для старых (загрязнённых) трубок значение Δ' = 0,015 мм. Тогда коэффициенты гидравлического трения для труб различных диаметров будут равны: λ1 = 0,11(Δ/d1)0,25 = 0,11(1/65)0,25 = 0,038 λ2= 0,11(Δ/d2)0,25 = 0,11(1/120)0,25 = 0,033 т. к. d1 =d3 = d4 =d5 =d6 =d7 =d9 = 65 мм, то λ1= λ3 = λ4 = λ5 = λ6 = λ7 = λ9 = 0,038; λ8 = 0,11(Δ/d8)0,25 = 0,11(1 /90)0,25 = 0.036; для труб змеевика λзм = 0,11(0,015 / 45)0,25 = 0,015. Определяем значения коэффициентов местных потерь по справочным данным. Все коэффициенты местных потерь должны быть отнесены к динамическому давлению за местным сопротивлением, кроме случаев, оговариваемых особо. Вентиль 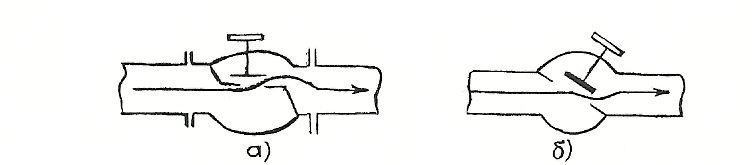 Для вентиля с прямым шпинделем примем ζвен = 4 Пробковый кран Для угла поворота пробкового крана α = 15° пробкового крана ζкр = 0.75. 3адвижка 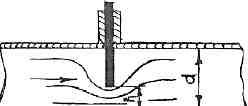 По высоте подъёма задвижки и h = 43 мм и диаметру трубы d =65 мм определяем степень открытия n = (d– h) / d = (65 – 43) / 65 = 0,34 а затем по таблице находим ζзад = 0,81. Диафрагма 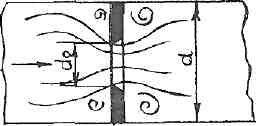 При диаметре отверстия диафрагмы d0 = 66 мм и диаметре трубы d = 65 мм коэффициент сжатия струи s определяется по формуле 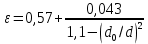 = =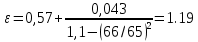 а коэффициент сопротивления диафрагмы – по формуле 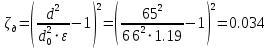 Внезапное расширение трубопровода 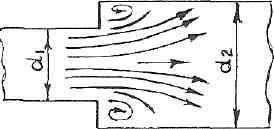 Значение коэффициента ζв.р. определяется по формуле 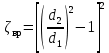 Для 2-го участка трубопровода 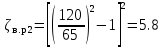 Для 8-ого участка трубопровода 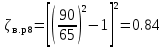 Внезапное сужение трубопровода 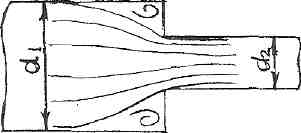 . .Определяем степень сжатия потока при сужении на 3-м участке п3 = (d3 /d2)2= (65/120)2 = 0.29 и по нему по таблице находим коэффициент внезапного сужения ζв.с3 =0,37 Наиболее резкое сужение трубопровода 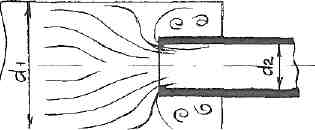 ζнрс9 = 1 – (d9 /d8)2 =1 –(65/90)2 = 0,48 Плавный поворот трубы (закруглённое колено, отвод) 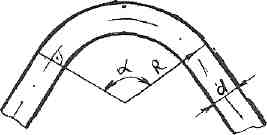 Коэффициент потерь в колене при α = 90° определяем по формуле . Для первого колена и для третьего колена при d3 = d7= 65 мм и R1 = R3 = 75 мм находим 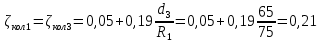 Для второго и четвертого колена при d4=d9= 50 мм и R1 = R3= 150 мм находим 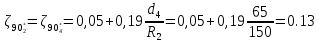 Так как углы поворота а для второго и четвёртого колена больше 90˚, то коэффициент а определяем по формуле : – для второго колена при α2= 132° 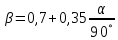 = 0,7 + 0,35 · 132 / 90 = 1,21; = 0,7 + 0,35 · 132 / 90 = 1,21;– для четвёртого колена при α4 = 125° 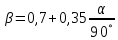 = 0,7 + 0,35 · 125 / 90 = 1,19; = 0,7 + 0,35 · 125 / 90 = 1,19;Тогда коэффициенты местных потерь для второго колена 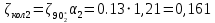 для четвёртого колена 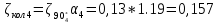 Змеевиковый теплообменник. По таблице и по схеме определяем коэффициенты местных сопротивлений для змеевикового теплообменника: вход в камеру ζвх.к =1,5; вход из камеры в трубки ζвх.т = 1,0; поворот на 180° в U–образной трубке ζU = 0,5; выход из трубок в камеру ζв.т =1,0; выход из камеры в патрубок ζв.к = 1,5. Найденные значения коэффициентов гидравлического сопротивления подставляем в уравнения и находим коэффициенты C1, C2, предварительно определив плотность пара при температуре t= 149о С по таблице ρ = 2.547 кг/м3. 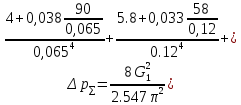 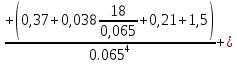 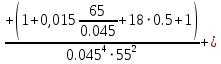 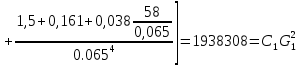 где С1= 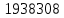 Для второй ветви 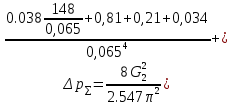 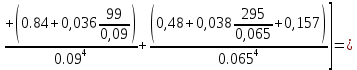 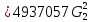 где С2 = 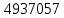 Определяем массовый расход в каждой ветви трубопровода по формуле 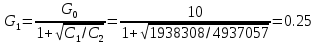 кг/с кг/с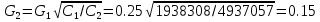 кг/с. кг/с.Проверка правильности расчёта расходов: G1+G2= 0.25+0.15= 0.4 кг/с = Gо. Определяем потери давления 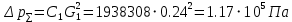 Мощность на валу насоса 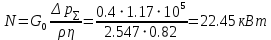 Приведённое решение предполагает квадратичный закон сопротивлений, когда потери не зависят от числа Рейнольдса. Проверим Квадратичный закон сопротивлений для чего определим числа Re для каждого трубопровода: 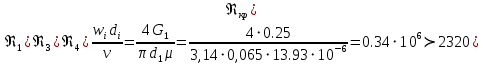 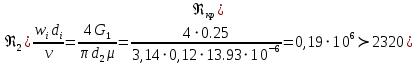 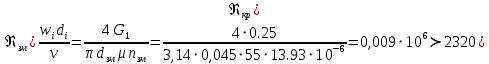 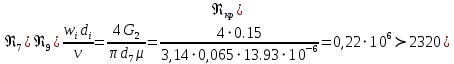 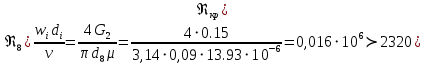 По найденными числам Рейнольдса уточняем все коэффициенты гидравлического трения. Так как движение турбулентное (Re > Reкр), то расчет ведем по формуле: 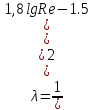 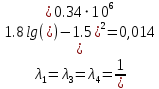 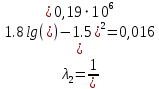 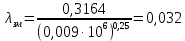 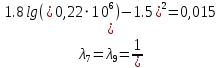 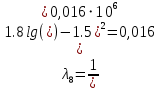 Найденные значения коэффициентов гидравлического сопротивления подставляем в уравнения и находим коэффициенты C1 , С2. 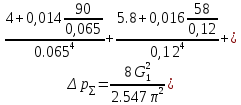 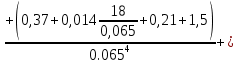 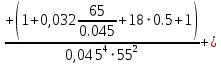 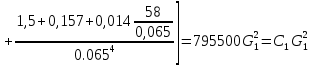 Где C1= 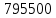 Для второй ветви: 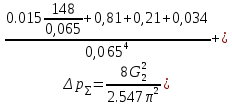 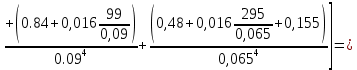 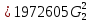 C2= 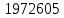 Определяем массовый расход в каждой ветви трубопровода по формуле: 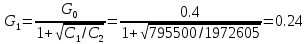 кг/с кг/с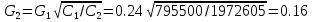 кг/с кг/сПроверка правильности расчёта расходов: G1+G2= 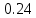 + +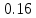 = 0.4 кг/с = Gо = 0.4 кг/с = GоОпределяем потери давления: 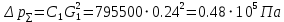 Мощность на валу насоса: 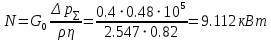 Графическая частьПроизведем расчёт и построение напорной и пьезометрической линий для одной ветви. Последовательно для каждого местного сопротивления и между ними рассчитаем гидравлические потери Δhтр и Δhмс ΣΔhп. Определим скоростные напоры для участков с разными диаметрами трубопровода. Расчетное сечение 1-2: Потери напора от питающего резервуара до рассматриваемого сечения 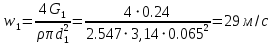 Δhтр = 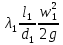 = =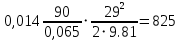 м мΔhмс = 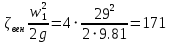 м мΔhп = Δhтр+ Δhмс = 996 м Скоростной напор в рассматриваемом сечении 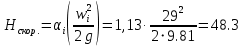 м мРасчетное сечение 2-3: Потери напора от питающего резервуара до рассматриваемого сечения 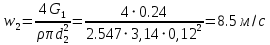 Δhтр = 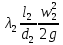 = =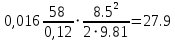 м мΔhмс = 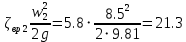 м мΔhп = Δhтр + Δhмс = 49,2 м Скоростной напор в рассматриваемом сечении 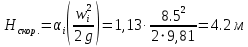 Расчетное сечение 3-4: Потери напора от питающего резервуара до рассматриваемого сечения 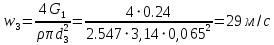 Δhтр = 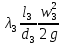 = =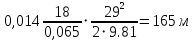 Δhмс3 = 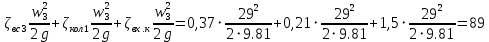 м мΔhп = Δhтр + Δhмс = 254 м Скоростной напор в рассматриваемом сечении 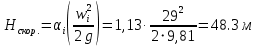 Расчетное сечение 4-5: Потери напора от питающего резервуара до рассматриваемого сечения 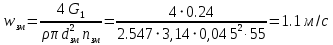 Δhтр = 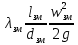 = =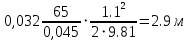 Δhмс = 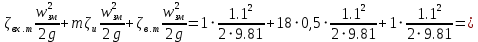 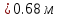 Δhп = Δhтр + Δhмс = 3.58 м Скоростной напор в рассматриваемом сечении 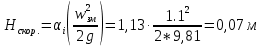 Расчетное сечение 5-6: Потери напора от питающего резервуара до рассматриваемого сечения 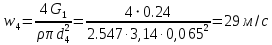 Δhтр = 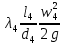 = =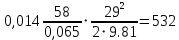 м мΔhмс = 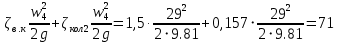 м мΔhп= Δhтр+ Δhмс= 603 м Скоростной напор в рассматриваемом сечении 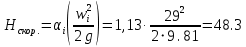 м мРезультаты сведем в таблицу
Определяем начальный пьезометрический напор 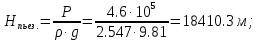 и начальный полный напор 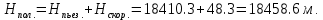 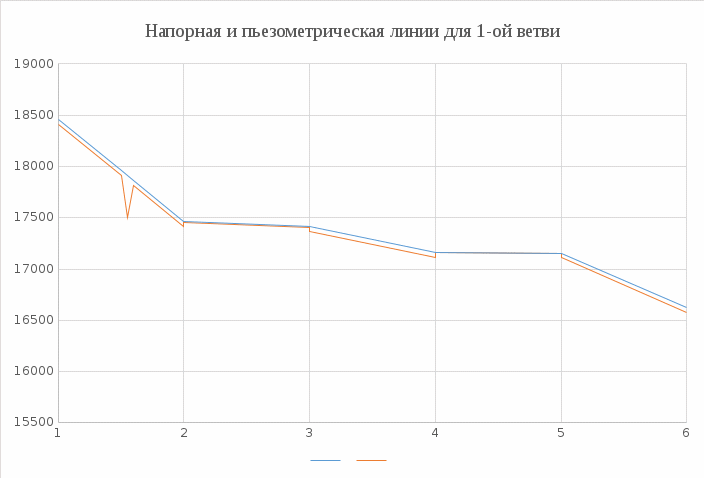  — Полный напор Электрификация и автоматизация горного производства — Пьезометрический напор Линия полного напора представляет гидравлический уклон, т.е. падение напора (энергии) на единицу длины l. Так как обычный запас энергии убивает вдоль потока, то линия полного напора всегда нисходящая, а гидравлический уклон положительный. Пьезометрическая линия графический отражает напоры вдоль потока без скоростного напора поэтому она располагается всегда ниже напорной линии. В отличие от напорной линии пьезометрическая может не только понижаться вдоль потока, но и повышаться. На участках трубопровода, где происходит внезапное сужение потока, должно наблюдаться резкое понижение пьезометрического напора. Наоборот, на участках с внезапным расширением потока должно наблюдаться восстановление пьезометрического напора ЗаключениеВ ходе курсовой работы были произведены гидравлические расчеты по определению расходов и потерь на отдельных участках трубопровода. На основании расчетов произведено построение линий полного и пьезометрического напора для одной из ветвей трубопровода. Использованная литератураКудинов, В. А. Гидравлика: учебное пособие / В.А. Кудинов, Э.М. Карташова. - 2-е изд., перераб. и доп. - М.: Высшая школа, 2007. - 199 с. Гидравлика, гидромашины, гидроприводы: учебник для вузов / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов [и др.]. - 2-е изд., перераб. Репринтное издание. - М.: Альянс, 2013. - 423 с. Метревели, В. Н. Сборник задач по курсу гидравлики с решениями: учебное пособие для вузов / В.Н. Метревели. - М.: Высшая школа, 2007. - 192 с. Гидравлика и гидравлические машины: учебник для студентов вузов / А. А. Угинчус. - 5-е изд., стереотип. - М.: ОАО "ТИД "Аз-book", 2009. - 395 с. Киселёв П. Г. и др. Справочник по гидравлическим расчётам. М.: Энергия, 1974. Идельчик И. Е. Справочник по гидравлическим сопротивлениям. М.–Л.: Госэнергоиздат, 1961. Альтшуль А. Д., Киселёв П. Г. Гидравлика и аэродинамика. М.: Стройиздат, 1975. Лебедев П. Д., Щукин А. А. Теплоиспользующие установки промышленных предприятий. М: Энергия, 1970. Аэродинамический расчёт котельных установок. Нормативный метод. М.–Л.: Госэнергоиздат, 1961. Краснощёков Е. А., Сукомел А. С. Задачник по теплопередаче. М.: Энергия, 1975. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

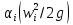 , м
, м