Министерство образования и науки российской федерации Федеральное государственное бюджетное образовательное учреждение высшего образования тюменский индустриальный университет
 Скачать 206.16 Kb. Скачать 206.16 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» Институт транспорта Кафедра транспорта углеводородных ресурсов Контрольные задания по дисциплине «Надежность технических систем и техногенный риск» Вариант 10 Выполнил: студент гр. ЭОТб(до)зу-15-4(ИДДО) Сухоруков Евгений Викторович Проверил: Тюмень, 2018 Задание 1 Определить в соответствии с вариантом (табл. 3.1) один из показателей надежности (вероятность безотказной работы P(t), время безотказной работы t или интенсивность отказов λ в период нормальной эксплуатации). Таблица 3.1 Задачи по определению надежности объекта
Задание 2 Зная значения надежности составных элементов, вычислить вероятность безотказной работы системы. Ответить на вопрос: надежна ли данная система. Предложить мероприятия по увеличению надежности, рассчитать систему с резервным элементом. 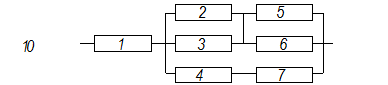
Решение: Параллельно соединенные элементы соответствуют логической операции «И», а последовательно соединенные – логической операции «ИЛИ». Соединенные логическим условием «И», объединяются по принципу их перемножения, при этом считается, что параметр головного события рассчитывается как произведение: P = P1 · P2 Соединенные логическим условием «ИЛИ», объединяются по принципу логического сложения, а их соответствующие параметры образуют в частных случаях, например, для n = 2: Pi = 2 = P1 + P2 – P1 · P2; Тогда, для первого варианта 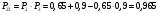 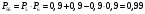 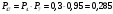 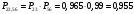 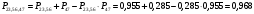 Вероятность безотказной работы системы 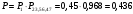 Для второго варианта 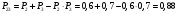 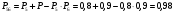 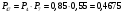 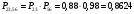 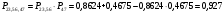 Вероятность безотказной работы системы 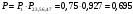 Для третьего варианта 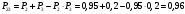 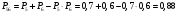 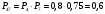 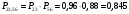 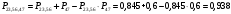 Вероятность безотказной работы системы 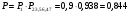 Мероприятия по увеличению надежности: вероятность безотказной работы первого элемента должна быть как можно выше. Резервный элемент подключаем параллельно, тогда Для первого варианта 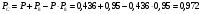 Для третьего варианта 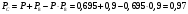 Для второго варианта 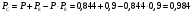 Задание 3 Рассчитать вероятность безотказной работы сложной системы для схем (рис. 3.4). 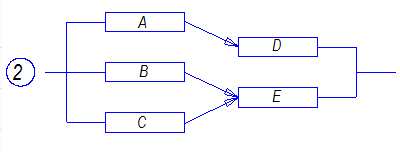 Рис. 3.4. Расчетные схемы
Для определения вероятности безотказной работы системы или надёжности её функционирования используют несколько методов. Здесь принят метод прямого перебора. Метод состоит в том, что рассматриваются все возможные способы появления отказов, т. е. не отказал ни один элемент, отказал один элемент, два и т. д. В системе, изображённой на рис. 3.3, элементы имеют следующие вероятности безотказной работы: Р(А) = 0,9; Р(В) = 0,5; Р(С) = 0,6; Р(Д) = 0,7; Р(Е) = 0,8. Здесь А – событие «элемент А работает безотказно»; тогда Ā – событие «элемент А отказал». Аналогично определяются события для всех остальных элементов. Затем вычисляется вероятность состояния системы для каждого способа появления отказа. Результаты записываются в табл. 3.2. Р( 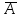 ) = 0,1; Р( ) = 0,1; Р(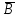 ) = 0,5; ) = 0,5; Р( 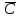 ) = 0,4; Р( ) = 0,4; Р(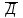 ) = 0,3; Р( ) = 0,3; Р(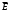 ) = 0,2. ) = 0,2.Таблица 3.2 Расчет надежности
Таким образом, система со сложным соединением элементов (подсистем) имеет вероятность безотказной работы 0,8668. Задание 4Оценить надежность оборудования в период нормальной эксплуатации. Задание выполнить в следующем порядке: 1) выбрать (в соответствии со специальностью) вид типового оборудования машиностроительного производства, выбор согласовать с преподавателем; 2) построить «дерево неисправностей» или «дерево причин»; рассчитать надежность системы; оценить надежность оборудования; построить «дерево рисков»; рассчитать риск. Вариант 5 Формулировка задания Найти: 1) вероятность возникновения опасной ситуации при прикосновении человека к корпусу электрооборудования (рис. 3.12, а) или к металлическому корпусу бытового электроприбора (рис. 3.12, б), питающегося от сети с заземлённой нейтральной точкой трансформатора, при нарушении изоляции и пробое фазы на корпус; 2) риск гибели человека при возникновении этой опасной ситуации, по величине которого найти степень безопасности, считая деятельность профессиональной (вариант а) и непрофессиональной (вариант б).  Рис. 3.12. Прикосновение человека к электрооборудованию (а) и к бытовому электроприбору (б) Описание причин возникновения опасной ситуации Вероятность возникновения опасной ситуации при прикосновении человека к корпусу электрооборудования Ро.с (вентиль «И») определяется вероятностью прикосновения к корпусу Рпр (СВЛЭ), вероятностью нахождения корпуса под напряжением Рн (СВЛЭ) и вероятностью отказа систем защиты Ротк(СВЛЭ). Вероятность Рпр («ИЛИ») может быть обусловлена одной из следующих причин: – неосторожностью Р1(ИСОДД); – случайностью Р2(ИСОДД); – нарушением правил электробезопасности и инструкций по эксплуатации Р3 (ИСОДД). Вероятность Рн («ИЛИ») обусловлена нарушением изоляции в результате действия следующих причин: – высокие пусковые токи Р4 (ИСОДД); – механические повреждения Р5 (ИСОДД); – естественное старение изоляции Р6 (ИСОДД). Вероятность Ротк («инвертор») обусловлена эффективностью срабатывания защиты (зануление или защитное отключение) Рзащ (ИСОДД). Риск гибели человека при поражении электрическим током R(«И») обусловлен вероятностью возникновения опасной ситуации Ро.с (ИСОДД), прохождением через человека смертельно опасного тока Ро.т (СВЛЭ), вероятностью нахождения человека под током длительное время, превышающее допустимое Рвр (ИСОДД), вероятностью неблагоприятного воздействия психофизиологических факторов Рп.ф (ИСОДД) и эффективностью применения средств пер- вой помощи при поражении током («инвертор») Рп.п (ИСОДД). Вероятность Ро.т («И») обусловлена вероятностью снижения сопротивления тела человека Рс.ч (ИСОДД), сопротивления пола Рс.п (ИСОДД) и обуви Рс.об (ИСОДД) до значений, которые в сумме приведут к появлению смертельно опасного тока. Исходные данные для расчёта
Построение структурных схем Вероятность возникновения опасной ситуации при прикосновении человека к корпусу электрооборудования 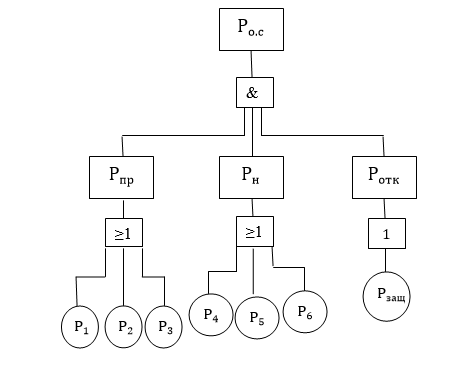 Риск гибели человека 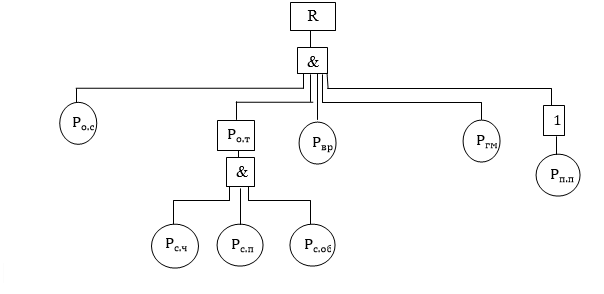 Составление формул, расчёт вероятности возникновения опасной ситуации и риска гибели человека: 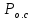 = =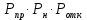 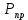 = Р1 + Р2 + Р3 + Р1 · Р2 – Р2 · Р3 – Р3 · Р1 + Р1· Р2 · Р3 = Р1 + Р2 + Р3 + Р1 · Р2 – Р2 · Р3 – Р3 · Р1 + Р1· Р2 · Р3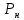 = Р4 + Р5+ Р6+ Р4 · Р5 – Р5 · Р6 – Р6 · Р4 + Р4· Р5 · Р6 = Р4 + Р5+ Р6+ Р4 · Р5 – Р5 · Р6 – Р6 · Р4 + Р4· Р5 · Р6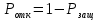 = 1 – 0,30 = 0,70 = 1 – 0,30 = 0,70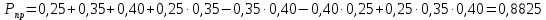 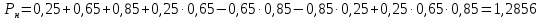 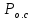 = =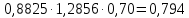 R= 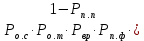 ) )Ро.т = Рс.ч·Рс.п ·Рс.об = 0,35·0,35·0,75 = 0,092 R 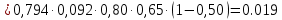 Вывод: Данная профессиональная деятельность относится к третьей категории безопасности как опасная работа с R = 10-3 – 10-2. Риск гибели человека в данной системе можно уменьшить, прежде всего, увеличением эффективности применения средств первой помощи при поражении током. Задание 5 1. Определить сокращение продолжительности жизни (СПЖ), риск R и выборку R–1 для вариантов, представленных в табл. 3.7. Таблица 3.7 Исходные данные для определения риска сокращения продолжительности жизни при радиоактивном загрязнении
2. Установить связь между размерностями степени загрязнения и дозы облучения. Решение: Доза облучения за всю жизнь после образования загрязнения: D = 2,7·10-7·К·П = 2,7·10-7·0,65·50· 105 = 0,8775 Бк/м2 Сокращение продолжительности жизни: СПЖ = 500·D = 500·0,8775 = 438,75 суток Величина риска потерь за жизнь: R = 4·10-5·СПЖ = 4·10-5·438,75 = 1755·10-5 суток Выборка R-1: R-1 = 1/R = 57 суток-1 Ответ: D = 0,8775 Бк/м2; СПЖ = 438,75 суток; R = 1755·10-5 суток; R-1 = 57 с Задание 6Определить величину риска и время, через которое ожидается появление признаков заболевания вибрационной болезнью у работников цеха, применяющих при исполнении трудовых обязанностей ручной вибрационный инструмент (варианты представлены в табл. 3.8).Результаты расчета представить в графическом виде. Сделать выводы. Таблица 3.8 Исходные данные для расчета величины риска и времени ожидаемого появления признаков заболевания вибрационной болезнью у работников
Решение: Риск заболевания от действия локальной вибрации: R = 10(0,05·Lw- 8)· 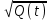 Q(t) = 1/15 = 0,067 (так как 15 работников) 1 работник: R1 = 100,05·142-8· 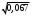 = 0,033 = 0,033 2 работника: R2 = 100,05·142-8· 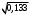 = 0,046 = 0,0463 работника: R3 = 100,05·142-8· 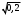 = 0,056 = 0,0564 работника: R4 = 100,05·142-8· 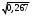 = 0,065 и так далее. = 0,065 и так далее.Представим в графическом виде риск заболевания от действия локальной вибрации 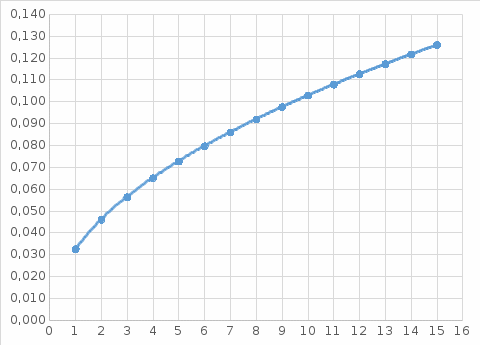 Время, через которое ожидается появление признаков заболевания вибрационной болезнью у работников цеха t1 = 0,067/0,033 = 2,1 года t2 = 0,133/0,046 = 2,9 года t3 = 0,2/0,056 = 3,6 года t4 = 0,267/0,065 = 4,1 года и так далее 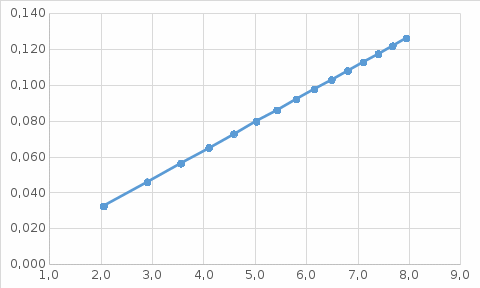 На диаграмме представлена зависимость риска заболевания от времени. На диаграмме видно, что чем дольше работает работник, тем больше вероятность появления признаков заболевания вибрационной болезнью у работников цеха. Риск заболевания от действия общей вибрации: R = 10(0,05·Lw- 8,9)· 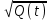 1 работник: R1 = 100,05·142-8,9· 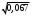 = 0,004 = 0,004 2 работника: R2 = 100,05·142-8,9· 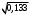 = 0,006 = 0,0063 работника: R3 = 100,05·142-8,9· 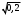 = 0,007 = 0,0074 работника: R4 = 100,05·142-8,9· 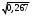 = 0,008 и так далее. = 0,008 и так далее.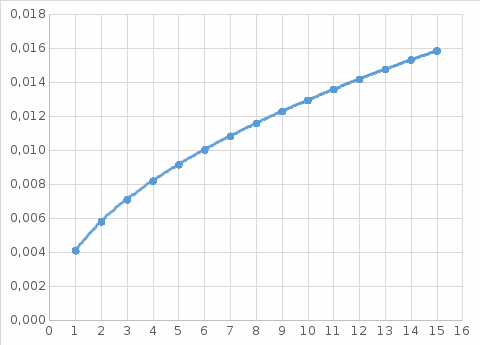 Величина риска, через которое ожидается появление признаков заболевания вибрационной болезнью у работников цеха от действия общей вибрации значительно ниже, чем от действия локальной вибрации. Время, через которое ожидается появление признаков заболевания вибрационной болезнью у работников цеха t1 = 0,067/0,004 = 16,3 года t2 = 0,133/0,006 = 23 года t3 = 0,2/0,007= 28,2 года t4 = 0,267/0,008 = 32,6 года и так далее. 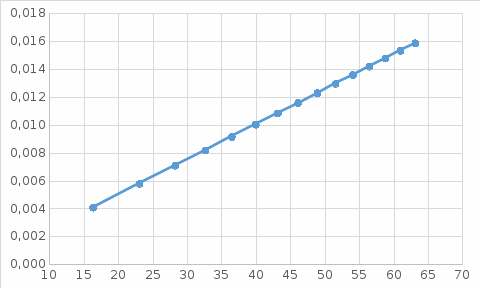 Признаки заболевания вибрационной болезнью у работников цеха от действия общей вибрации проявляются значительно позже, чем от действия локальной вибрации. Список использованной литературы Сердюк В.С. Надежность технических систем и техногенный риск: конспект лекций / В.С. Сердюк, А.Б. Корчагин. – Омск: Изд-во ОмГТУ, 2007. – 86 с. Надежность технических систем и техногенный риск: метод. указания к самостоятельной работе студентов / сост.: В.С. Сердюк, А.Б. Корчагин. – Омск: Изд-во ОмГТУ, 2007. – 89 с. Надёжность технических систем и техногенный риск: метод. указания к выполнению практ. работ / сост.: В.С. Сердюк, А.Б. Корчагин, М.Г. Нинилина. – Омск: Изд-во ОмГТУ, 2007. – 20 с. Сборник задач по теории надёжности / А.М. Половко [и др.]; под ред. А.М. Половко. – М.: Сов. радио, 1972. – 408 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

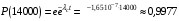 .
.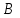 ∩
∩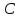 ∩
∩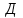 ∩Е
∩Е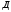 ∩
∩