опорные векторы. Қадырбек Диар Мәнжазба ITmed 301 (1). Мнжазба Таырып
 Скачать 484.97 Kb. Скачать 484.97 Kb.
|
|
Қазақстан Республикасының Ғылым және Білім минитрлігі Қ. Жұбанов атындағы Ақтөбе өңірлік мемлекеттік университеті Физика-Математика факультеті Информатика және АТ кафедрасы 6В06106 – IT – медицина мамандығы  Мәнжазба Тақырып. Тiрек векторлар әдісі. Орындаған: Қадырбек Диар. Тексерген: Ермагамбетов Т. Ақтөбе, 2022 жыл Жоспар: SVM тірек векторлар әдісін қарастыру Алгоритмнің салмағын реттеу және қарапайым DIY іске асыру Алгоритмнің артықшылықтары мен кемшіліктері Кіріспе Бұл мақалада біз тірек векторларының әдісін қарастырамыз (ағылш. SVM, Support Vector Machine) жіктеу тапсырмасы үшін. Алгоритмнің негізгі идеясы ұсынылады, оның салмағын реттеу және қарапайым DIY іске асыру бөлшектеледі. Дат Iris Дат dataset мысалында линей R^2 простран кеңістігінде сызықтық бөлінетін/бөлінбейтін деректермен жазылған алгоритмнің жұмысы және оқу/болжамды визуализация көрсетіледі. Сонымен қатар, алгоритмнің артықшылықтары мен кемшіліктері, оның модификациялары айтылады. Шешілетін міндет: Біз екілік (тек екі сынып болған кезде) жіктеу мәселесін шешеміз. Біріншіден, алгоритм сынып белгілері алдын-ала белгілі болатын оқу үлгісіндегі нысандарда оқытылады. Әрі қарай, дайындалған алгоритм кейінге қалдырылған/сынақ үлгісіндегі әрбір нысан үшін сынып белгісін болжайды. Сынып белгілері мәндерді қабылдай алады . Объект-вектор c N кеңістіктегі белгілермен . Оқыту кезінде алгоритм кеңістіктен аргумент — объектіні қабылдайтын және сынып белгісін беретін функцияны құруы керек . Алгоритм туралы жалпы сөздер: Жіктеу міндеті мұғаліммен бірге оқуды білдіреді. SVM-мұғаліммен оқыту алгоритмі. Машиналық оқытудың көптеген алгоритмдерін осы мақаладан көруге болады ("Машиналық оқыту әлемінің картасы"бөлімін қараңыз). SVM регрессиялық тапсырмалар үшін де қолданыла алатындығын қосу керек, бірақ бұл мақалада SVM классификаторы талданады.SVM-дің классификатор ретіндегі басты мақсаты-екі класты қандай да бір оңтайлы түрде бөлетін кеңістіктегі гиперпланды бөлу теңдеуін табу.Алгоритмнің және (оқытудың) таразыларын реттегеннен кейін, салынған гиперпланның бір жағына түсетін барлық нысандар бірінші класс, ал екінші жағына түсетін Нысандар екінші класс ретінде болжанады. Функцияның ішінде алгоритм салмағымен объект белгілерінің сызықтық тіркесімі бар, сондықтан SVM сызықтық алгоритмдерге жатады. Бөлу гиперпланын әртүрлі тәсілдермен салуға болады, бірақ SVM салмақтары және сынып объектілері бөлу гиперпланынан мүмкіндігінше алыс болатындай етіп реттеледі. Басқаша айтқанда, алгоритм алшақтықты барынша арттырады (ағылш. margin) гиперплан мен оған ең жақын орналасқан сынып объектілері арасында. Мұндай нысандар тірек векторлары деп аталады (2 суретті қараңыз). Алгоритмнің атауы осыдан шыққан 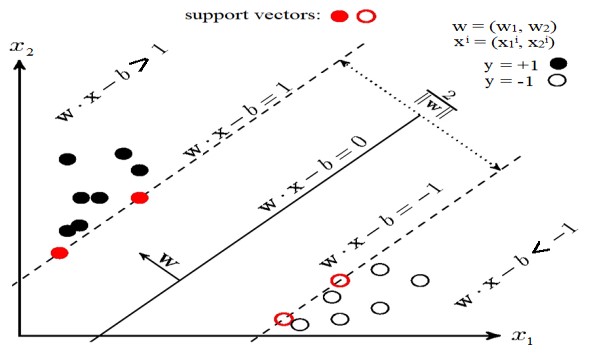 Сурет 2. SVM (сурет негізі осы жерден) SVM таразысын баптау ережелерін егжей тегжейлі шығару: Бөлу гиперпланы үлгі нүктелерінен мүмкіндігінше алыс тұруы үшін жолақтың ені максималды болуы керек. Вектор-бөлу гиперпланына қалыпты вектор. Мұнда және одан әрі біз екі вектордың скалярлық көбейтіндісін немесе деп белгілейміз . Вектордың проекциясын табайық, оның ұштары векторға әр түрлі кластардың тірек векторлары болып табылады . Бұл проекция полос көрсетеді бөлу жолақтар (3 суретті қараңыз): 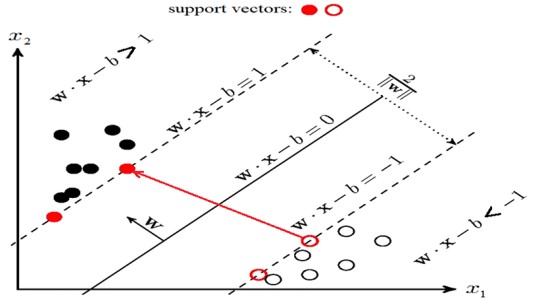 Сурет 3. Таразыны баптау ережелерін шығару (сурет негізі осы жерден) Шегініспен (ағылш. margin) x объектісінің сынып шекарасынан шамасы деп аталады . Алгоритм объектіде шегініс теріс болған кезде ғана қате жібереді (әр түрлі белгілер болған кезде). Егер объект бөлгіш жолақтың ішіне кірсе. Егер x нысаны дұрыс жіктелсе және бөлу жолағынан біршама қашықтықта болса. Мұның бәрі бізде сыныптар сызықтық түрде бөлінгенге дейін жақсы. Алгоритм сызықтық бөлінбейтін деректермен де жұмыс істей алатындай етіп, жүйемізді аздап түрлендірейік. Алгоритмге оқу объектілерінде қателіктер жіберуге мүмкіндік берейік, бірақ сонымен бірге қателіктердің аз болуына тырысамыз. Әр объектідегі қатенің шамасын сипаттайтын қосымша айнымалылар жиынтығын енгізейік . Минимизацияланған функционалдылыққа жалпы қате үшін айыппұл енгізейік: Біз алгоритмдегі қателер санын есептейміз (қашан m<0). Мұны айыппұл (пенальти) деп атайық. Содан кейін барлық нысандар үшін айыппұл шекті функция болып табылатын әрбір нысан үшін айыппұл сомасына тең болады (суретті қараңыз.4):Әрі қарай, біз айыппұлды қатенің мәніне сезімтал етеміз ("минусқа" неғұрлым көп кетсе — соғұрлым көп айыппұл) және сонымен бірге объектіні сынып шекарасына жақындатқаны үшін айыппұл саламыз. Ол үшін қатенің шекті функциясын шектейтін функцияны алайық (4 суретті қараңыз): 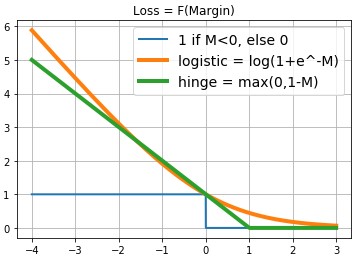 Айыппұл өрнегіне қосылған кезде, термин бір объект үшін жұмсақ саңылауы бар (soft-margin SVM) классикалық SVM шығын фукциясын аламыз: - жоғалту функциясы, ол жоғалту функциясы. Біз оны қолмен жүзеге асыруда градиентті түсіру арқылы азайтамыз. Біз таразыны өзгерту ережелерін шығарамыз, мұнда түсу қадамы: Есеп мысалы: Шығын функциялары: import numpy as np import matplotlib.pyplot as plt %matplotlib inline xx = np.linspace(-4,3,100000) plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0') plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)') plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)') plt.title('Loss = F(Margin)') plt.grid() plt.legend(prop={'size': 14}); 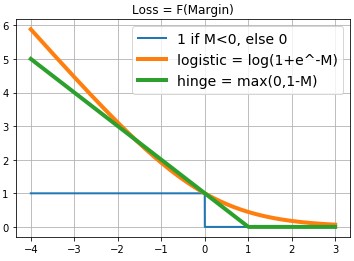 Алдымен қажетті кітапханаларды және сызықты сызу функциясын кесіңіз: import numpy as np import warnings warnings.filterwarnings('ignore') import matplotlib.pyplot as plt import matplotlib.lines as mlines plt.rcParams['figure.figsize'] = (8,6) %matplotlib inline from sklearn.datasets import load_iris from sklearn.decomposition import PCA from sklearn.model_selection import train_test_split def newline(p1, p2, color=None): # функция отрисовки линии #function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib ax = plt.gca() xmin, xmax = ax.get_xbound() if(p2[0] == p1[0]): xmin = xmax = p1[0] ymin, ymax = ax.get_ybound() else: ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0]) ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0]) l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color) ax.add_line(l) return l Мүмкіндік векторының кеңейту функциясының коды: def add_bias_feature(a): a_extended = np.zeros((a.shape[0],a.shape[1]+1)) a_extended[:,:-1] = a a_extended[:,-1] = int(1) return a_extended Инициализация функциясының коды: def __init__(self, etha=0.01, alpha=0.1, epochs=200): self._epochs = epochs self._etha = etha self._alpha = alpha self._w = None self.history_w = [] self.train_errors = None self.val_errors = None self.train_loss = None self.val_loss = None Оқыту функциясының коды: def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1 if len(set(Y_train)) != 2 or len(set(Y_val)) != 2: raise ValueError("Number of classes in Y is not equal 2!") X_train = add_bias_feature(X_train) X_val = add_bias_feature(X_val) self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1]) self.history_w.append(self._w) train_errors = [] val_errors = [] train_loss_epoch = [] val_loss_epoch = [] for epoch in range(self._epochs): tr_err = 0 val_err = 0 tr_loss = 0 val_loss = 0 for i,x in enumerate(X_train): margin = Y_train[i]*np.dot(self._w,X_train[i]) if margin >= 1: # классифицируем верно self._w = self._w - self._etha*self._alpha*self._w/self._epochs tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) else: # классифицируем неверно или попадаем на полосу разделения при 0 self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs) tr_err += 1 tr_loss += self.soft_margin_loss(X_train[i],Y_train[i]) self.history_w.append(self._w) for i,x in enumerate(X_val): val_loss += self.soft_margin_loss(X_val[i], Y_val[i]) val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int) if verbose: print('epoch {}. Errors={}. Mean Hinge_loss={}'\ .format(epoch,err,loss)) train_errors.append(tr_err) val_errors.append(val_err) train_loss_epoch.append(tr_loss) val_loss_epoch.append(val_loss) self.history_w = np.array(self.history_w) self.train_errors = np.array(train_errors) self.val_errors = np.array(val_errors) self.train_loss = np.array(train_loss_epoch) self.val_loss = np.array(val_loss_epoch) Деректерді дайындау блогы: = load_iris() = iris.data  = iris.target
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) Инициализация және оқыту блогы:
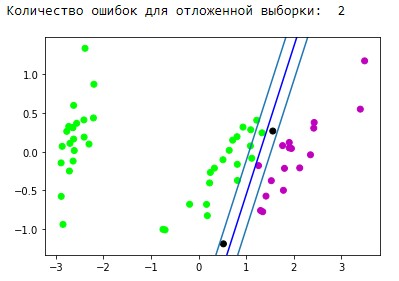
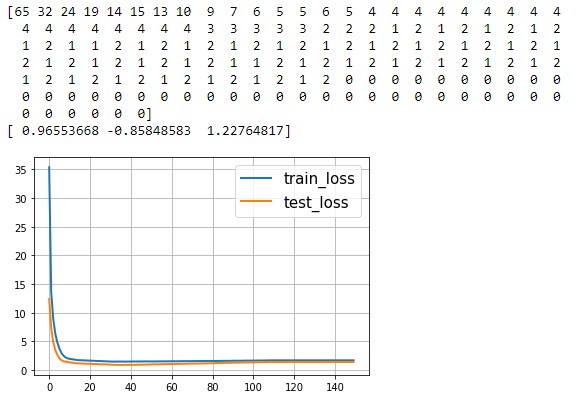 plt.show() plt.show() Алынған бөлу жолағының визуализация блогы: 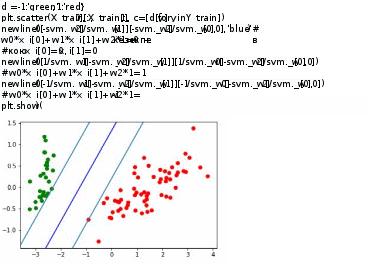 Болжамды бейнелеу блогы: y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error  print('Количество ошибок для отложенной выборки: ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 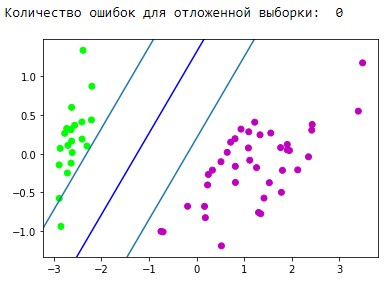 Деректерді дайындау блогы:  iris = load_iris() X = iris.data Y = iris.target
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020) Инициализация және оқыту блогы:
plt.show() 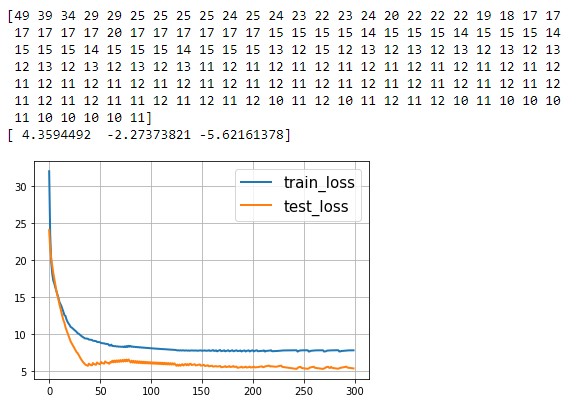 Алынған бөлу жолағының визуализация блогы: d = {-1:'green', 1:'red'}  plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') # в w0*x_i[0]+w1*x_i[1]+w2*1=0 поочередно # подставляем x_i[0]=0, x_i[1]=0 newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1 newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 plt.show() 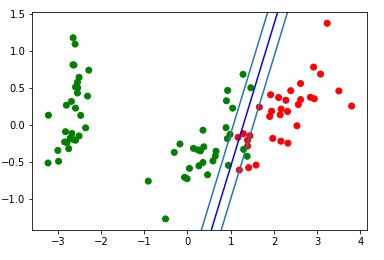 Анимация жасау коды:  import matplotlib.animation as animation from matplotlib.animation import PillowWriter def one_image(w, X, Y): axes = plt.gca() axes.set_xlim([-4,4]) axes.set_ylim([-1.5,1.5]) d1 = {-1:'green', 1:'red'} im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y]) im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue') # im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1 # im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1 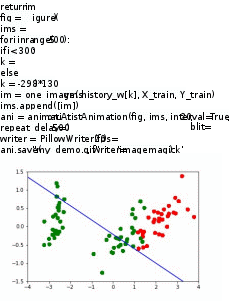 Болжамды бейнелеу блогы: y_pred = svm.predict(X_test) y_pred[y_pred != Y_test] = -100 # find and mark classification error  print('Количество ошибок для отложенной выборки: ', (y_pred == -100).astype(int).sum()) d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred]) newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
 Қорытынды Классикалық SVM артықшылықтары мен кемшіліктері: Артықшылықтары: үлкен өлшемді белгілер кеңістігімен жақсы жұмыс істейді; шағын көлемді деректермен жақсы жұмыс істейді; алгоритм қауіпсіздік жастығы ретінде жіктеу қателерін азайтуға мүмкіндік беретін бөлу жолағын барынша арттырады; алгоритм дөңес аймақтағы квадраттық бағдарламалау мәселесін шешуге дейін азаятындықтан, мұндай есептің әрқашан жалғыз шешімі болады (алгоритмнің белгілі бір гиперпараметрлері бар гиперпланды бөлу әрқашан бір). Кемшіліктері: ұзақ оқу уақыты (Үлкен деректер жиынтығы үшін); шудың тұрақсыздығы: оқу деректеріндегі шығарындылар тірек бұзушы нысандарға айналады және бөлетін гиперпланның құрылысына тікелей әсер етеді; сыныптардың сызықтық бөлінбеуі жағдайында белгілі бір тапсырма үшін ең қолайлы ядролар мен түзеткіш кеңістіктерді құрудың жалпы әдістері сипатталмаған. Пайдалы деректерді түрлендіруді таңдау-бұл өнер. Пайдаланған материалдар: https://medium.com/nuances-of-programming/метод-опорных-векторовпримеры-на-python-655455a2fd3b https://habr.com/ru/company/ods/blog/484148/ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
