Многопараметрическая оптимизация. Многопараметрическая оптимизация
 Скачать 237.21 Kb.
|
Многопараметрическая оптимизация.Всякая сложная система состоит из отдельных более простых подсистем (элементов). Поэтому естественно, решая задачу многоцелевой оптимизации для системы в целом, разработчик неизбежно должен ставить и решать задачи многоцелевой оптимизации для отдельных ее подсистем. При этом должна осуществляться координация (взаимное согласование) критериев оптимальности подсистем в соответствии с их назначением и связями, существующими между подсистемами. Совокупность показателей качества системы можно рассматривать как вектор, поэтому многоцелевую оптимизацию называют также векторной. Теория векторной оптимизации непрерывно развивается. Возрастает количество работ прикладного характера, выполненных с использованием методов и алгоритмов многоцелевой оптимизации. Обучение современным методам многоцелевой оптимизации с использованием ЭВМ является важным элементом в подготовке инженеров химиков-технологов, будущих разработчиков новых технологических процессов. ПОСТАНОВКА ЗАДАЧИ В данной статье метод роя частиц применяется для поиска оптимального расположения центра управления предприятием, в состав которого входят b-е число производственных объектов. Исходными данными для решения поставленной задачи являются: координаты xkи ykрасположения производственных объектов; удельные затраты uk(в относительных единицах – баллах) на коммуникационные связи между k-м объектом и центром управления (k = 1, …,b). Предметом поиска являются такие значения координат X и Y расположения центра управления, при которых затраты на реализацию коммуникационных связей между объектами и центром управления будут минимальны.  Критериальная функция для решения поставленной задачи примет вид:ИСХОДНЫЕ ДАННЫЕ
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ 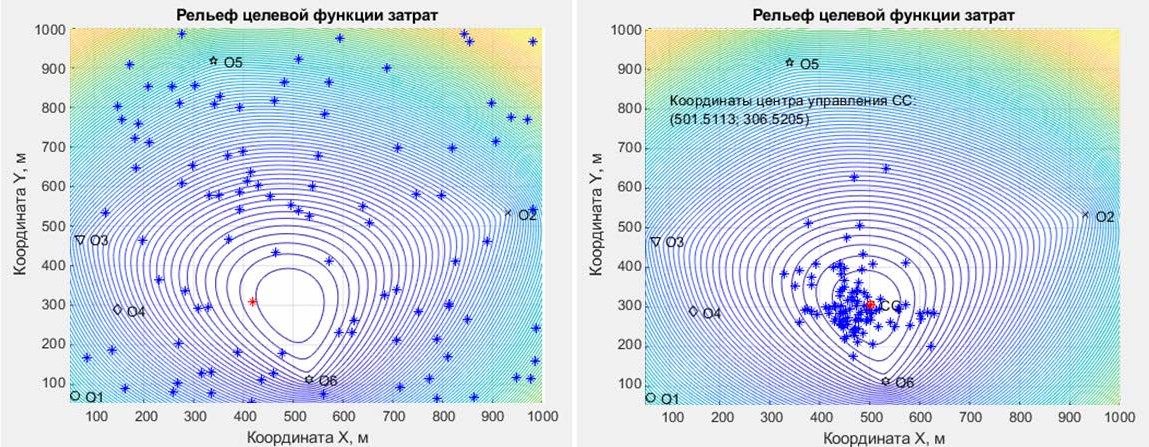 На основе составленного алгоритма была написана программа в среде MATLAB для поиска решения описанной выше задачи оптимизации. В соответствии с исходными данными было определено оптимальное расположение центра управления (X = 501,5; Y = 306,5), при этом целевая функция оказалась равной 81432,76. На рисунках 2 и 3 показаны скриншоты соответственно начала и конца работы алгоритма.Рис. 2. Исходное положение частиц Рис. 3. Результат работы программы Результаты, полученные методом роя частиц, сравнивались с результатами работы детерминированных методов оптимизации, таких как метод Гаусса-Зейделя и градиентный метод. Можно сделать вывод о том, что полученные результаты достоверны. Таким образом, при реализации программы было выявлено, что среди множества стохастических методов оптимизации метод роя частиц является достаточно простым в реализации, но точным с точки зрения математики. При этом надо найти оптимальное соотношение многих параметров, таких как количество частиц, коэффициенты ускорений, инерцию, что в целом может усложнить поиск решения задачи с большим количеством критериев. Также трудности могут возникнуть при выборе условия выхода из цикла. Заключение В работе был проведён анализ метода роя частиц при решении задач многокритериальной оптимизации. Разработан обобщённый алгоритм, применимый к задаче с любым количеством параметров. Предложено новое условие выхода из цикла – по требуемой точности. На основе разработанного алгоритма написана программа для решения двухпараметрической задачи оптимизации в среде MATLAB с графическим выводом решения. | ||||||||||||||||||||||||||||||||||