Лабораторная работа 3 по АИСД. Множества как объект
 Скачать 417.55 Kb. Скачать 417.55 Kb.
|
|
| Студент гр. 1305 | | |
| Студент гр. 1305 | | |
| Преподаватель | | |
Санкт-Петербург
2022
Цель работы
исследование алгоритмов для работы с двоичным (троичным) деревом.
Задание
Вариант 13
Вид дерева: Двоичный, разметка: симметричная, способ обхода: В глубину, задание: Количество вершин на глубине не более 2
Обоснование выбора способа представления деревьев
Дерево оформлено в виде класса, т.к. это наиболее удобный способ представления с точки зрения функционала, при этом временные затраты несущественны (отсылка ко 2 лабораторной работе)
Тестовый пример
Вершины обозначены в виде букв, поле - в виде точек. Например граф вида
B
A C
G
Будет иметь обход: B_A_C_G, где пройдено 4 узла, количество вершин на глубине не больше 2-3.
Результаты программы
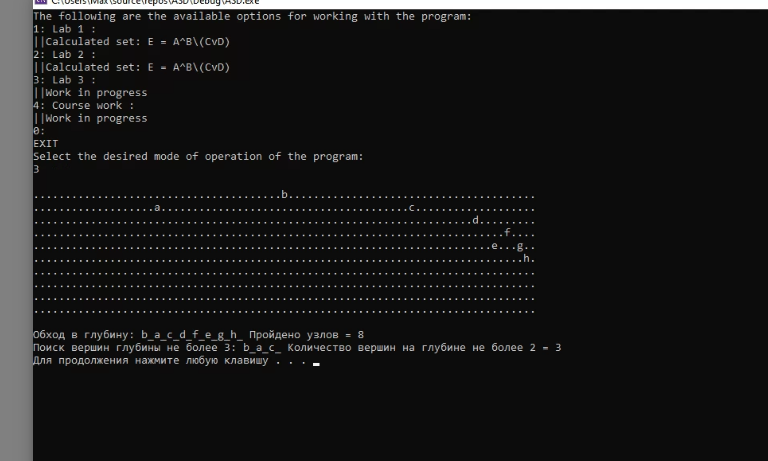
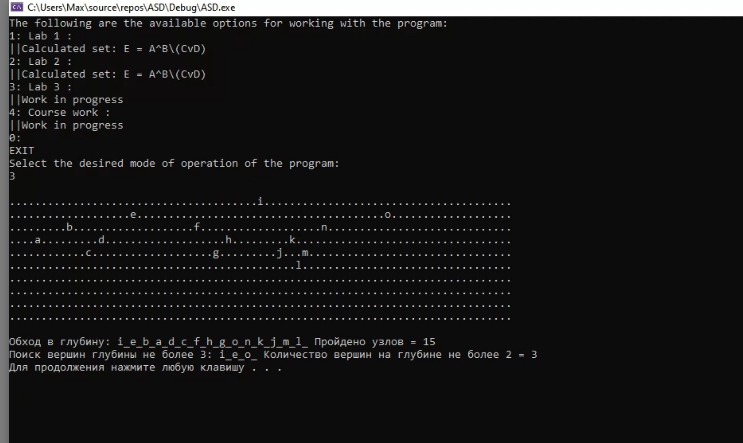
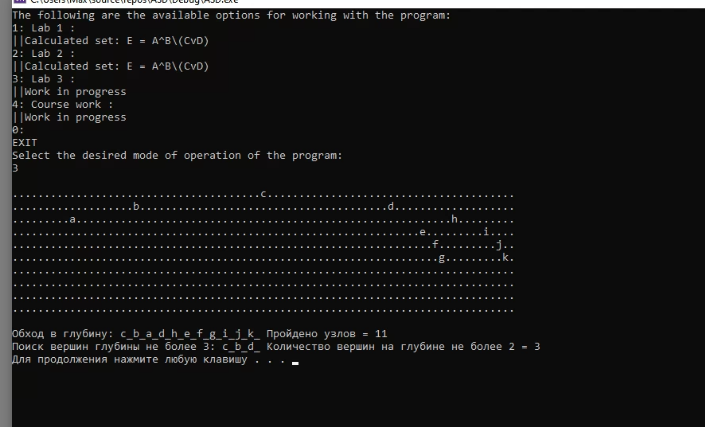
Оценки временной сложности
Создание дерева обладает сложностью O(log n), считающее количество узлов: O(1), сложность DFS - O(N), сложность, сложность обхода O(V + E), где V – количество вершин, E – количество ребер (если быть точным, то выбираем из V или E максимальное, т.е. O(E) или O(V))
Вывод
В итоге были исследованы алгоритмы работы с двоичным деревом, само дерево было предоставлено в виде класса, реализованы методы по обработке этого самого дерева, например DFS или симметричный обход.
Список использованной литературы.
“Методические указания по дисциплине «Алгоритмы и структуры данных, часть 1». Вып. 2209.“ Автор: П. Г. Колинько
Приложение
#include "Lab_3.h"
Tree::Tree(char nm, char mnm, int mxr) :
num(nm), maxnum(mnm), maxrow(mxr), offset(40), root(nullptr),
SCREEN(new char* [maxrow])
{
for (int i = 0; i < maxrow; ++i) SCREEN[i] = new char[80];
}
Tree :: Tree() {
for (int i = 0; i < maxrow; ++i) delete[]SCREEN[i];
delete[]SCREEN; delete root;
}
Node* Tree::MakeNode(int depth, Node *prt)
{
Node* v = nullptr;
int Y = (depth < rand() % 6 + 1) && (num <= 'z');
// int Y;
// cout << "Node (" << num << ',' << depth << ")1/0: "; cin >> Y;
if (Y) { // создание узла, если Y = 1
v = new Node;
v->prt = prt;
//v->d = num++; // разметка в прямом порядке (= «в глубину»)
v->lft = MakeNode(depth + 1, v);
v->d = num++;
v->rgt = MakeNode(depth + 1, v);
}
return v;
}
void Tree::OutTree()
{
clrscr();
OutNodes(root, 1, offset);
for (int i = 0; i < maxrow; i++)
{
SCREEN[i][79] = 0;
cout << "\n" << SCREEN[i];
}
cout << "\n";
}
void Tree::clrscr()
{
for (int i = 0; i < maxrow; i++)
memset(SCREEN[i], '.', 80);
}
void Tree::OutNodes(Node* v, int r, int c)
{
if (r && c && (c < 80)) SCREEN[r - 1][c - 1] = v->d; // вывод метки
if (r < maxrow) {
if (v->lft) OutNodes(v->lft, r + 1, c - (offset >> r)); //левый сын
if (v->rgt) OutNodes(v->rgt, r + 1, c + (offset >> r)); //правый сын
}
}
int Tree::DFS()
{
const int MaxS = 20; // максимальный размер стека
int count = 0;
STACK
S.push(root); // STACK <- root
while (!S.empty()) // Пока стек не пуст…
{
Node* v = S.pop(); // поднять узел из стека.
cout << v->d << '_'; count++; // выдать тег, счёт узлов
if (v->rgt) S.push(v->rgt); // STACK <- (правый сын)
if (v->lft) S.push(v->lft); // STACK <- (левый сын)
}
return count;
}
int Tree::DepthCounter(int NeedDepth)
{
const int MaxS = 20;
int count = 0, depth = 0;
STACK
S.push(root);
while (!S.empty())
{
Node* v = S.pop();
Node* VDepth = v;
depth = 1;
while (VDepth)
{
VDepth = VDepth->prt;
depth++;
}
cout << v->d << '_'; count++;
if (depth <= 2)
{
if (v->rgt) S.push(v->rgt);
if (v->lft) S.push(v->lft);
}
}
return count;
}
//main lab 3 function
void lab_3()
{
int n = 0;
Tree Tr('a', 'z', 10);
srand(time(nullptr));
setlocale(LC_ALL, "Russian");
Tr.MakeTree();
if (Tr.exist()) {
Tr.OutTree();
cout << endl << "Обход в глубину: ";
n = Tr.DFS();
cout << " Пройдено узлов = " << n;
cout << endl << "Поиск вершин глубины не более 3: ";
n = Tr.DepthCounter(2);
cout << " Количество вершин на глубине не более 2 = " << n;
}
}
