Математический анализ. Множество называется
 Скачать 88.07 Kb.
|
|
№1 Множество называется счетным, если все его элементы можно занумеровать, используя по одному разу все натуральные числа. Рациональные числа представляются несократимыми дробями с целым числителем и знаменателем. Множество дробей с данным знаменателем счётно, поэтому представимо в виде объединения счетного числа счетных множеств. Представим множество всех рациональных чисел в виде бесконечной таблицы (фото 1). Таким образом можно представить все рациональные числа. N-ая строка – это все несократимые дроби со знаменателем n, расположенные по возр. их модуля с чередующимися знаками. Очевидно, что в этой таблице находятся все рациональные числа. Используя прием диагонализации представим R в виде (фото 2) 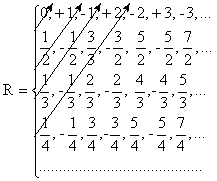  . Т.к R представилось в форме последовательности, то отсюда следует, что R – счетное множество. Для док-ва несчетности мн-ва R достаточно доказать, что существует хотя-бы 1 беск-ное подмн-во R, которое при этом не явл-ся счетным. Покажем, что таким подмн-ом явл-ся мн-во действительных чисел на интервале (0;1). Предположим, что мн-во допустимого бес-ого десятичных дробей на интервале (0;1) счетно. След-но, его элементы можно занумеровать и присвоить каждой дроби, соотв-ий номер (натур. число). Будем обозн-ть i-ю цифру после запятой у n-й дроби как ni. Все дроби из интервала (0;1) можно выписать в виде ряда по порядку нумеров: 0; 11 12 13 : : : 1i : : : 0; 21 22 23 : : : 2i : : : 0; 31 32 33 : : : 3i : : : 0; n1 n2 n3 : : : ni : : : Покажем, что не все бесконечные десятичные дроби из интервала (0;1) содержатся в этом списке. Построим новую беск-ную дробь по след. правилу: в качестве n-й цифры возьмем любую, кроме 0,9 и nn и так далее. В результате получим некоторую беск-ную дробь. Эта дробь будет допустимой, так как не содержит 9 в периоде, но и вообще не содержит 9. Она не является представлением 0. Она >0 и <1 => она принадлежит (0;1) и не содержится в списке. №2 Предел числовой последовательности – это предел последовательности элементов числового пространства. Числовое пространство – это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Метрическое пространство – это непустое мн-во, в котором между любой парой элементов, обладающих определенными св-вами, определено расстояние, называемое метрикой. Числовая послед-ность может иметь только 1 предел. Предположим, что послед-ность Хn имеет 2 различных предела b и a, причем b Выберем E>0 таким образом, чтобы Е- окрестности точек b и a не пересекались. Возьмем, например, E=(a-b)/3. Так как число b – предел последовательности Xn, то по заданному E>0 можно найти номер N такой, что Xn принадлежит Ue(b) для всех n ≥N. Поэтому вне интервала Ue(b) может оказаться лишь конечное число членов последовательности. В частности. Интервал Ue(a) может содержать лишь конечное число членов послед-сти. Это противоречит тому, что а – предел послед-сти (любая окрестность точки а должна содержать беск-ное число членов послед-сти). Полученное противоречие показывает, что послед-сть не может иметь 2 различных предела. Итак, сходящаяся послед-сть имеет только 1 предел. Последовательность Xn называется ограниченной снизу, если сущест-ет такое число С1, что все члены послед-сти удовлетворяют условию  т.е.  . Послед-сть Xn называется ограниченной сверху, если  Последовательность, ограниченную как снизу, так и сверху, называют ограниченной, если  Таким образом, послед-ность называют ограниченной, если мн-во ее значений ограничено. Если последовательность имеет предел, то она ограничена. Пусть последовательность  имеет предел, равный а. По определению предела для  найдем номер N такой, что при всех  имеет место неравенство  . Так как модуль суммы не превосходит суммы модулей, то:  поэтому при всех выполняется неравенство  Положим  , тогда  при всех  т.е. последовательность Xn ограничена№3 Послед-ность  называется бесконечно малой, если  т.е  Свойства: 1) Бескон-но малая посл-сть ограничена. 2) Сумма бесконечно малых посл-стей есть беск-но малая посл-сть. 3) Произведение беск-но малой посл-сти на ограниченнуб есть беск-но малая посл-сть. 4) Если элементы беск-но малой посл-сти равны одному и тому же числу C, то C=0. Док-во Пусть - бесконечно малая посл-сть, E – некоторое полож. Число. Пусть N – номер, такой, что  . Обозначим  числом А. Получим:   что и означает ограниченную посл-сть№4 Свойства пределов 1) Постоянный множитель c можно выносить за знак предела:  Пусть  тогда переменную Yn можно представить в виде  где an – бесконечно малая величина. Очевидно, что Поскольку  представляет собой бесконечно малую величину, то число с А является пределом послед-сти  : 2) Если существуют конечные пределы последовательностей  и  , то    Пусть  и  Тогда переменные  можно представить в виде:  где  и  - некоторые бесконечно малые величины. Тогда Учитывая, что  - бесконечно малая величина, получаем Аналогично:  Осталось распознать в выражении  что влечет за собой  Далее покажем, что отношение  можно представить в виде  Очевидно, что  где Следовательно,  3) Если существуют конечные пределы последовательностей и  , то Интуитивные соображения. Пусть  . Тогда где – некоторая бесконечно малая величина. Следовательно,  №5 Пусть заданы две последовательности  и  Если  и, начиная с некоторого номера,  , то выполняется неравенство  . (теорема сжатия, принцип двустороннего ограничения) Если и существует номер  , что для любого  выполняется неравенство  , то последовательность  сходится, причем  №6 |