теория вероятности. отчет. Моделирование и обработка вероятностных событий, связанных и имитацией игры в кости

Название	Моделирование и обработка вероятностных событий, связанных и имитацией игры в кости
Анкор	теория вероятности
Дата	20.05.2022
Размер	32.57 Kb.
Формат файла
Имя файла	отчет.docx
Тип	Отчет #539870

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра АСУ

Отчет

о лабораторной работе № 2

по дисциплине «Теория вероятности»

на тему: «Моделирование и обработка вероятностных событий, связанных и имитацией игры в кости»

Выполнила:

студентка группы ИС-20а

Морозова М.А.

Проверили:

Пряхин В.В.

Теплова О.В.

Донецк – 2021

Постановка задачи:
Составить программу, которая моделирует бросание пары игральных костей и реализует имитацию игры в кости с учетом того, что кости могут быть не с симметричными гранями.
Основные требования:

В процессе выполнения лабораторной работы необходимо выполнить следующее:

Разработать алгоритм и написать программу, реализующую имитатор бросания пары костей с равновероятными и разновероятными выпадениями граней.

По схеме случаев вычислить теоретические и эмпирические вероятности событий появления граней при бросании костей.

Имитация игры должна быть реализована в двух режимах:

в ручном режиме (например, бросание кости по нажатию определенной клавиши);

в автоматическом режиме (производится моделирование бросания кости с сохранением результатов, объем выборки от 10000 до 50000);

Для выбора режимов работы моделирующей программы организовать меню.

Моделирующая программа должна быть написана с обязательным использованием принципов ООП. В качестве объекта (класса) обязательно должен быть описан такой объекты как игральная кость.

Работа реализованного имитатора игры должна быть проанализирована с помощью статистического критерия «Хи-квадрат».

Для наглядного отображения полученной информации необходимо предусмотреть вывод полученной статистической информации в табличном и графическом виде. Предусмотреть возможность построения следующих графиков:

построение графика теоретического полигона частот результата игры и гистограммы частот практических результатов игры, полученных в ходе проведенного имитационного эксперимента для заданного количества опытов.

Индивидуальное задание

№ варианта

Количество граней

Доминирующая грань

1-го кубика

Доминирующая грань

2-го кубика

1-й кубик

2-й кубик

Грань

Значение

Грань

Значение

11

8

8

8

0,4

8

0,6

№ грани

Теоретическая вероятность

Количество выпадений грани

Практическая вероятность

1

0,08571

925

0,092500

2

0,08571

870

0,087000

3

0,08571

829

0,082900

4

0,08571

878

0,087800

5

0,08571

850

0,085000

6

0,08571

926

0,092600

7

0,08571

917

0,091700

8

0,40000

3805

0,380500

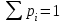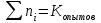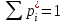№ грани

Теоретическая вероятность

Количество выпадений грани

Практическая вероятность

1

0,05714

594

0,059400

2

0,05714

566

0,056600

3

0,05714

575

0,057500

4

0,05714

481

0,048100

5

0,05714

605

0,060500

6

0,05714

607

0,060700

7

0,05714

438

0,043800

8

0,60000

6134

0,613400

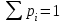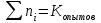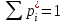Листинг

// lab2.cpp : Этот файл содержит функцию "main". Здесь начинается и заканчивается выполнение программы.

//

#include

#include
class kub

{

private:

int gran;

float* veroyatn;

int* kolvo_vip;

int bros;

public:

kub(int n)

{

gran = n;

float j = 0.0;

veroyatn = new float[gran];

kolvo_vip = new int[gran];

for (int i = 0; i < gran; i++)

{

j = (float)j + 1.0 / gran;

veroyatn[i + 1] = j;

printf("\n%.2f ", veroyatn[i + 1]);

printf("%d", i+1);

kolvo_vip[i] = 0;

}

}

kub(int n, int domin, float znach){

gran = n;

printf("Кубик c одной доминирующей гранью\n");

printf("Доминирующая грань %d Теоретическая вероятность ее выпадения %.2f\n", domin, znach);

float j = 0.0;

veroyatn = new float[gran + 1];

kolvo_vip = new int[gran];

veroyatn[0] = 0;

for (int i = 0; i < gran; i++)

{

printf("\t%d\t", i+1);

if (i == domin - 1) j = j + znach;

else j = j + ((1 - znach) / (gran - 1));

veroyatn[i + 1] = j;

printf(" %1.5f\n", veroyatn[i + 1]);

kolvo_vip[i] = 0;

}

}

void brosok(int n, int* rezultat) // свойство бросок(номер броска)

{

bros = n;

double slush_ver;

rezultat = 0;

slush_ver = (rand() % 100) / (100 1.0);

for (int i = 0; i < gran; i++)

{

if (slush_ver <= veroyatn[i + 1]) { rezultat = i + 1; break; }

else rezultat = gran;

}

for(int i=0; i
if (rezultat == i+1) kolvo_vip[i]++;

}

void Print()

{

float Prakt_ver;

printf("\n№ грани|Теоретическая вероятность|Количество выпадений|Практическая вероятность");

for (int i = 0; i < gran; i++)

{

Prakt_ver = (float)kolvo_vip[i] / bros;

printf("\n %d | %1.5f | %d | %f ", i+1, veroyatn[i + 1] - veroyatn[i], kolvo_vip[i], Prakt_ver);

}

}

void get_znash(int i, float ver, int* vipad)

{

ver = veroyatn[i + 1] - veroyatn[i];

vipad = kolvo_vip[i];

}

kub()

{

delete[]veroyatn;

delete[]kolvo_vip;

}

};
void main()

{

setlocale(LC_ALL, "RUS");

bool br = 0;int bros;

int rez1[10000], rez2[10000];

float ver1[8], ver2[8];

int vipad1[8], vipad2[8], i = 0;

float xi1 = 0, xi2 = 0, prom = 0, prem = 0;

kub kubik1 = kub(8, 8, 0.4);

kub kubik2 = kub(8, 8, 0.6);

while (br == 0)

{

printf("Введите количество бросков больше 0\nКолличество бросков=");

scanf_s("%d", &bros);

if (bros > 0) br = 1;

else printf("Вы ввели %d Значение не удовлетворяет условие\n", bros);

}

printf("\n1 - бросить сразу %d раз\n2 - одноразовый бросок по нажатию кнопки\n", bros);

int vibor1;

scanf_s("%d", &vibor1);

switch (vibor1){

case 1:

{

printf("Вы бросили %d раз", bros);

for (i = 0; i < bros; i++)

{

kubik1.brosok(bros, &rez1[i]);

kubik2.brosok(bros, &rez2[i]);

}

break; }

case 2:

{

printf("Вы выбрали режим броска по нажатию\n");

for (i = 0; i < bros; i++)

{

kubik1.brosok(bros, &rez1[i]);

kubik2.brosok(bros, &rez2[i]);

printf("\nРезультат подбрасывания кубиков = %d %d\n", rez1[i], rez2[i]);

system("pause");

}

break; }
}

kubik1.Print();

kubik2.Print();

for (i = 0; i < 8; i++)

{

kubik1.get_znash(i, &ver1[i], &vipad1[i]);

kubik2.get_znash(i, &ver2[i], &vipad2[i]);

}

for (i = 0; i < 8; i++)

{

prem = ver1[i] * bros;

prom = vipad1[i] - prem;

xi1 = xi1 + (prom * prom) / prem;

prem = ver2[i] * bros;

prom = vipad2[i] - prem;

xi2 = xi2 + (prom * prom) / prem;

}

printf("\nX^2 первого куба=%f\nX^2 второго куба=%f\n", xi1, xi2);

system("pause");

exit(1);

}

Результат работы программы

Кубик c одной доминирующей гранью

Доминирующая грань 8 Теоретическая вероятность ее выпадения 0,40

1 0,08571

2 0,17143

3 0,25714

4 0,34286

5 0,42857

6 0,51429

7 0,60000

8 1,00000

Кубик c одной доминирующей гранью

Доминирующая грань 8 Теоретическая вероятность ее выпадения 0,60

1 0,05714

2 0,11429

3 0,17143

4 0,22857

5 0,28571

6 0,34286

7 0,40000

8 1,00000

Введите количество бросков больше 0

Колличество бросков=10000
1 - бросить сразу 10000 раз

2 - одноразовый бросок по нажатию кнопки

1

Вы бросили 10000 раз

№ грани|Теоретическая вероятность|Количество выпадений|Практическая вероятность

1 | 0,08571 | 925 | 0,092500

2 | 0,08571 | 870 | 0,087000

3 | 0,08571 | 829 | 0,082900

4 | 0,08571 | 878 | 0,087800

5 | 0,08571 | 850 | 0,085000

6 | 0,08571 | 926 | 0,092600

7 | 0,08571 | 917 | 0,091700

8 | 0,40000 | 3805 | 0,380500

№ грани|Теоретическая вероятность|Количество выпадений|Практическая вероятность

1 | 0,05714 | 594 | 0,059400

2 | 0,05714 | 566 | 0,056600

3 | 0,05714 | 575 | 0,057500

4 | 0,05714 | 481 | 0,048100

5 | 0,05714 | 605 | 0,060500

6 | 0,05714 | 607 | 0,060700

7 | 0,05714 | 438 | 0,043800

8 | 0,60000 | 6134 | 0,613400

X^2 первого куба=26,273689

X^2 второго куба=53,610653
Кубик c одной доминирующей гранью

Доминирующая грань 8 Теоретическая вероятность ее выпадения 0,40

1 0,08571

2 0,17143

3 0,25714

4 0,34286

5 0,42857

6 0,51429

7 0,60000

8 1,00000

Кубик c одной доминирующей гранью

Доминирующая грань 8 Теоретическая вероятность ее выпадения 0,60

1 0,05714

2 0,11429

3 0,17143

4 0,22857

5 0,28571

6 0,34286

7 0,40000

8 1,00000

Введите количество бросков больше 0

Колличество бросков=5
1 - бросить сразу 5 раз

2 - одноразовый бросок по нажатию кнопки

2

Вы выбрали режим броска по нажатию
Результат подбрасывания кубиков = 5 8

Для продолжения нажмите любую клавишу . . .
Результат подбрасывания кубиков = 4 1

Для продолжения нажмите любую клавишу . . .
Результат подбрасывания кубиков = 8 5

Для продолжения нажмите любую клавишу . . .
Результат подбрасывания кубиков = 8 8

Для продолжения нажмите любую клавишу . . .
Результат подбрасывания кубиков = 8 8

Для продолжения нажмите любую клавишу . . .
№ грани|Теоретическая вероятность|Количество выпадений|Практическая вероятность

1 | 0,08571 | 0 | 0,000000

2 | 0,08571 | 0 | 0,000000

3 | 0,08571 | 0 | 0,000000

4 | 0,08571 | 1 | 0,200000

5 | 0,08571 | 1 | 0,200000

6 | 0,08571 | 0 | 0,000000

7 | 0,08571 | 0 | 0,000000

8 | 0,40000 | 3 | 0,600000

№ грани|Теоретическая вероятность|Количество выпадений|Практическая вероятность

1 | 0,05714 | 1 | 0,200000

2 | 0,05714 | 0 | 0,000000

3 | 0,05714 | 0 | 0,000000

4 | 0,05714 | 0 | 0,000000

5 | 0,05714 | 1 | 0,200000

6 | 0,05714 | 0 | 0,000000

7 | 0,05714 | 0 | 0,000000

8 | 0,60000 | 3 | 0,600000

X^2 первого куба=4,166667

X^2 второго куба=5,000000