КУРСОВОЙ ПРОЕКТ расчет. Моделирование индукционного нагрева
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
КУРСОВОЙ ПРОЕКТ ТЕМА: МОДЕЛИРОВАНИЕ ИНДУКЦИОННОГО НАГРЕВА Введение На сегодняшний день развитие численных методов позволяет успешно выполнять моделирование различных физических процессов, что широко используется во многих отраслях. Освоение инструментов компьютерного инженерного моделирования позволяет выполнять научно-исследовательские работы (линейных прочностных, динамических и тепловых задач; решения контактных задач; проведения геометрически нелинейных расчетов) при многократно сниженных затратах и риске по сравнению с проведением натурных испытаний, которые не всегда оправдывают затраты. Компьютерное моделирование играет важнейшую роль в современных условиях рыночной экономики, уменьшая себестоимость и время разработки нового. Реализация новой методологии обучения и методического обеспечения конструкторской подготовки специалистов, опирающейся на использовании в образовательном процессе возможностей CAD-технологий и конечно-элементных (CAE) пакетов, будет способствовать повышению до мирового уровня квалификаций кадров для инновационной деятельности. CAE (англ. Computer-aided engineering) – общее название для программ или программных пакетов, предназначенных для инженерных расчётов, анализа и симуляции физических процессов. Расчётная часть пакетов чаще всего основана на численных методах решения дифференциальных уравнений (метод конечных элементов, метод конечных объёмов, метод конечных разностей и др.). Одним из основных преимуществом применения подобных технологий – это возможность замены натурного или полунатурного эксперимента на виртуальное моделирование, что в свою очередь дает возможность прогнозировать поведение разрабатываемых конструкций уже на этапе их проектирования и минимизирует затраты на экспериментальную отработку. ТЕРЕТИЧЕСКАЯ ЧАСТЬ На данной частоте глубина проникновения токов в холодную сталь составляет примерно 0.25 мм. В процессе нагрева изменяются свойства слоев металла (удельное сопротивление, теплопроводность, теплоемкость и др.), поэтому нагреваемый металл целесообразно разбить на слои в зоне нагрева. На глубине проникновения необходимо выделить два слоя равной толщины (для учета насыщения стали в зоне выделения максимальной полезной мощности). Для учета изменения тепловых свойств стали, а также более точного построения кривой насыщения в металле выделим еще 4-5 слоев за первыми двумя. Толщина слоев при удалении от поверхности металла возрастает в геометрической прогрессии. Например, третий слой в 3 раза больше второго, четвертый в 3 раза больше третьего и т.д. Суммарная толщина слоев должна быть в 5-10 раз больше глубины проникновения токов в металл, так как в процессе нагрева величина глубины проникновения увеличивается. В процессе расчета будем дискретно (по шагам) изменять свойства слоев с ростом температуры. Требуется провести не менее пяти шагов расчета (табл. 1). Таблица 1
Задачу нестационарной теплопередачи, в принципе, необходимо рассматривать как нелинейную, так как теплоемкость и теплопроводность металла зависят от температуры. Однако в этом случае время расчетов многократно возрастает, и такая задача не всегда имеет решение (итерационный процесс не сходится, и в этом случае необходимо уменьшить шаг расчета по времени). В случае если требуемый шаг расчета по времени получается очень маленьким (больше десяти точек за один шаг), проще с целью экономии машинного времени каждый раз при смене шага расчета вводить новые значения теплопроводности и теплоемкости в метки блоков слоев металла. На время расчетов значительное влияние оказывают: частота источника электромагнитного поля в задаче магнитного поля переменных токов; количество блоков с отличными от нуля значениями теплоемкости и плотности. Для минимизации времени расчетов выставляем "прикидочный" режим в обеих задачах, а в задаче нестационарного теплообмена исключаем теплообмен внешней поверхности нагреваемого металла с окружающей средой, так как нагрев происходит относительно быстро и потери во внешнюю среду незначительны. Для того чтобы исключить индуктор из расчетов поля температур, на границах индуктора присваиваем ребрам метки с граничным условием заданной температуры. В метке блока с медью индуктора задаемся нулевым значением теплоемкости и плотности. Воздух, окружающий нагреваемую заготовку и индуктор, также желательно исключить из расчетов поля температур при нестационарном теплообмене. Для этого на внешней границе металла задаем свойства метки ребер, соответствующие граничному условию нулевого теплового потока через границу. В этом случае теплообмен между поверхностью металла и воздухом будет отсутствовать. Тем не менее, хотя "воздух" и "индуктор" исключены из тепловых расчетов в свойствах меток, соответствующих этим блокам, необходимо указать конечное значение теплопроводности. Значение, в принципе, может быть любым (рекомендуется λ = 1). В этом случае в "воздухе" за ребром с присвоенным граничным условием нулевого теплового потока будет наблюдаться некоторое распределение температур. Здесь следует понимать, что формирование картины температур в блоке с неизвестными температурами и заданной величиной теплопроводности (в данном случае блок с меткой "воздух") обеспечивается только введенным граничным условием. Иными словами, поле температур в "воздухе", не отражая реальной картины распределения, подстраивается к рассчитанной с наибольшей точностью реальной картине температур в слоях металла. Поскольку в связанных расчетах необходимо пользоваться одним файлом модели (*.mod), метки с введенными граничными условиями нулевого теплового потока и заданной температуры должны присутствовать под теми же именами и в электромагнитном расчете и для них также должны быть записаны граничные условия. В данном случае уместно задать однородное граничное условие Неймана (Ht = 0), которое является естественным для границ блоков без метки. 2. ПРАКТИЧЕСКАЯ ЧАСТЬ На каждом шаге необходимо провести связанный расчет задач магнитного поля переменных токов и нестационарной теплопередачи. При этом необходимо определить начальные условия моделирования: Необходимо определить начальную магнитную проницаемость слоев металла. Для этого проводим пробный расчет электромагнитного поля в слоях, подставляя значения магнитной проницаемости примерно в соответствии с кривой намагничивания. Считаем, что напряженность поля на поверхности металла составляет 103..104 А/м, а на глубине проникновения токов в холодный металл 0.5..1 А/м. После проведения пробного расчета определяем средние напряженности поля в слоях металла и корректируем магнитные проницаемости слоев. Для сокращения объема вычислений будем считать, что магнитная проницаемость слоев за время нагрева остается неизменной. Для задачи нестационарной теплопередачи необходимо задаться начальной температурой. Для этого проводим расчет температурного поля с мощностью тепловыделения во всех блоках модели, равной нулю, и заданной величиной температуры (293°К) на всех ребрах с метками. Связываем полученную задачу с задачей нестационарной теплопередачи на первом шаге. В итоге схема связанных расчетов будет выглядеть так, как показано на рис. 1. Для удобства дальнейшей работы с моделью на каждом из шагов расчета создаем новые файлы задач и сразу связываем их между собой в соответствии со схемой. 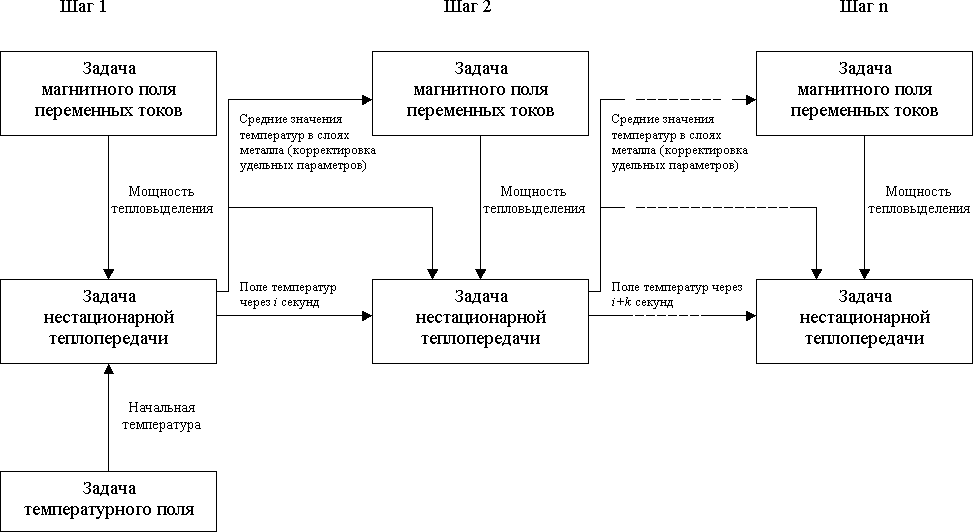 Рис. 1. Схема выполнения связанных расчетов Исходные данные: Толщина слоя под закалку: δ = 1 мм Температура поверхности изделия в конце нагрева: tкон = 750 ± 20 °C Перепад температур в слое под закалку: Δt ≤ 100 °C Перепад температур по поверхности нагреваемого участка: Δt ≤ 150 °C Время нагрева: τнагр ≤ 25 с. Ток в первичной обмотке согласующего трансформатора: 2- 50 А. Частота источника тока: 100 кГц. Форма кривой тока – чистая синусоида. Величина тока в индукторе: 3...20 кА. Зазор между индуктором и нагреваемой заготовкой : 2- 5 мм. Глубина проникновения токов в холодную сталь: 0,25мм. Выделим слои на глубине проникновения токов. Примем суммарную толщину слоев =1,7мм; При толщине первых 2-х слоев n, - 32*n=1,7 ; n = 0.05мм; 1-й слой 0,05 мм; 2-й слой 0,05 мм; 3-й слой 0,1 мм; 4-й слой 0,2 мм; 5-й слой 0,4 мм; 6-й слой 0,9 мм; Таблица 2. Шаги расчета процесса
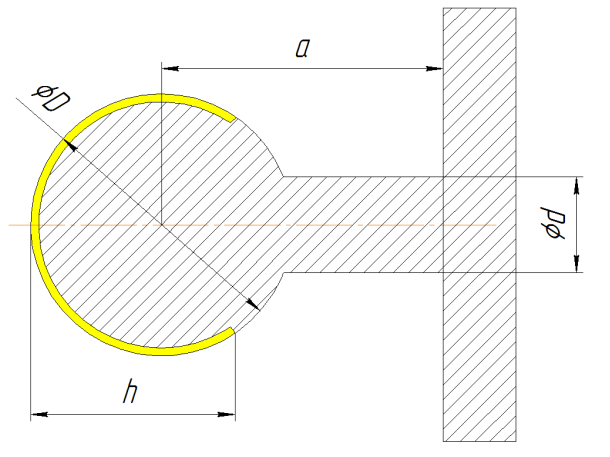 Рис.1 Нагреваемая деталь (шаровая опора)   Рис.2 Внешний вид нагреваемой детали и индуктора Рис.2 Внешний вид нагреваемой детали и индуктораГеометрические размеры нагреваемой детали: a = 40мм; d = 18мм; h = 5мм; D = 30мм. На каждом шаге нам необходимо произвести связанный расчет задач магнитного поля переменных токов и нестационарной теплопередачи. Создадим задачу магнитного поля переменных токов для шага 1 в среде Elcut: 1. Начинаем выполнение работы с составления файла модели (*.mod) – он будет общим для всех файлов задач на каждом шаге расчета. Геометрическая модель для приведенного примера показана на рис.3 В зоне нагрева в соответствии с рекомендациями, приведенными выше, выделяем несколько слоев, в которых в процессе расчета будем менять удельные тепловые и электрические свойства. 2. Необходимо определить начальную магнитную проницаемость слоев металла. Для этого проводим пробный расчет электромагнитного поля в слоях, подставляя значения магнитной проницаемости примерно в соответствии с кривой намагничивания. Считаем, что напряженность поля на поверхности металла составляет 103...104А/м, а на глубине проникновения токов в холодный металл 0,5...1 А/м. После проведения пробного расчета определяем средние напряженности поля в слоях металла и корректируем магнитные проницаемости слоев. Для сокращения объема вычислений будем считать, что магнитная проницаемость слоев за время нагрева остается неизменной. Проводим пробный электромагнитный расчет и определяем средние напряженности в слоях металла (рис.7). По полученным значениям напряженности поля в слоях (рис.8) определяем их магнитные проницаемости (рис.8) и производим повторный расчет. 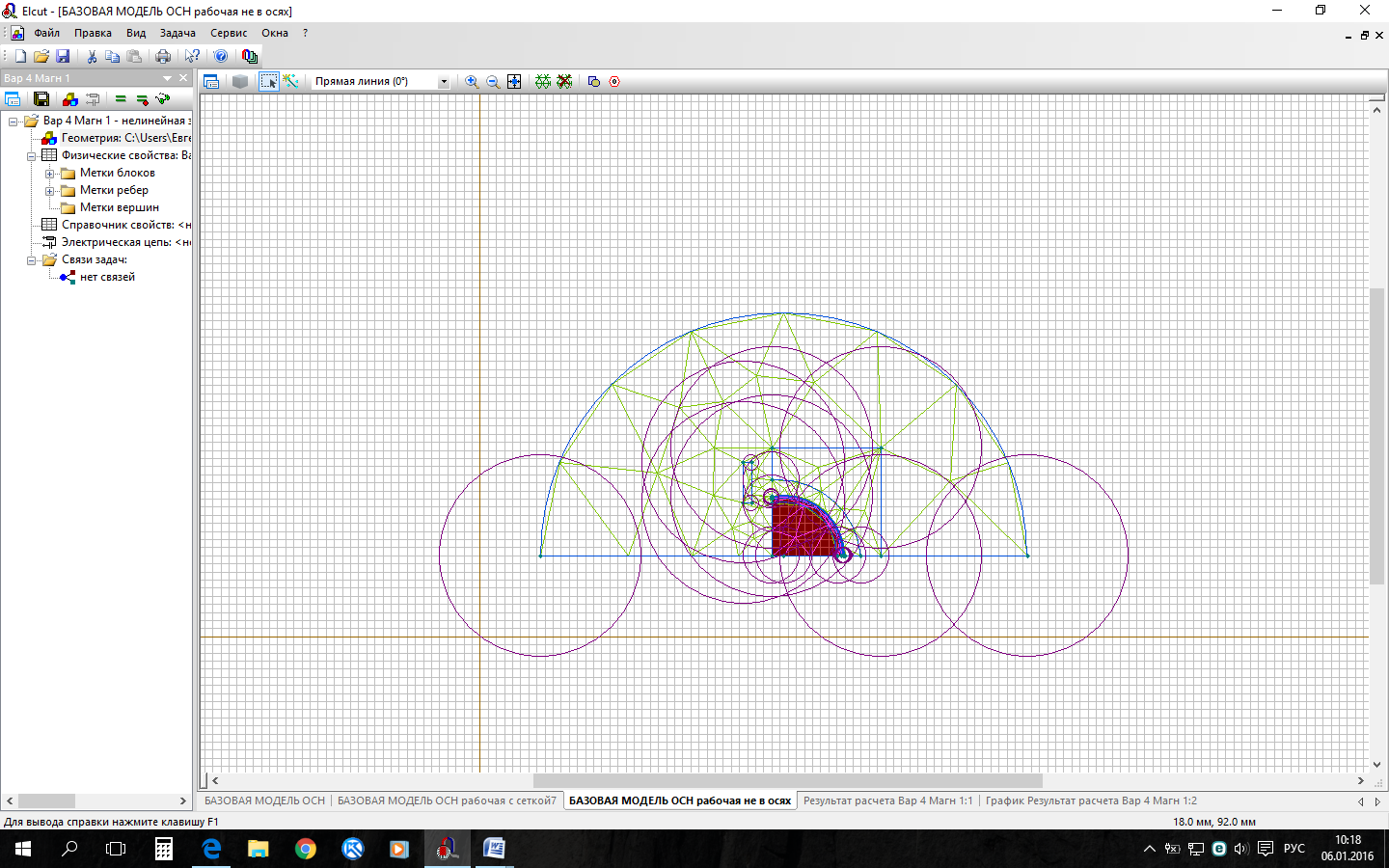 Индуктор Деталь Экран    Рис.3 Геометрическая модель процесса нанесенной сеткой 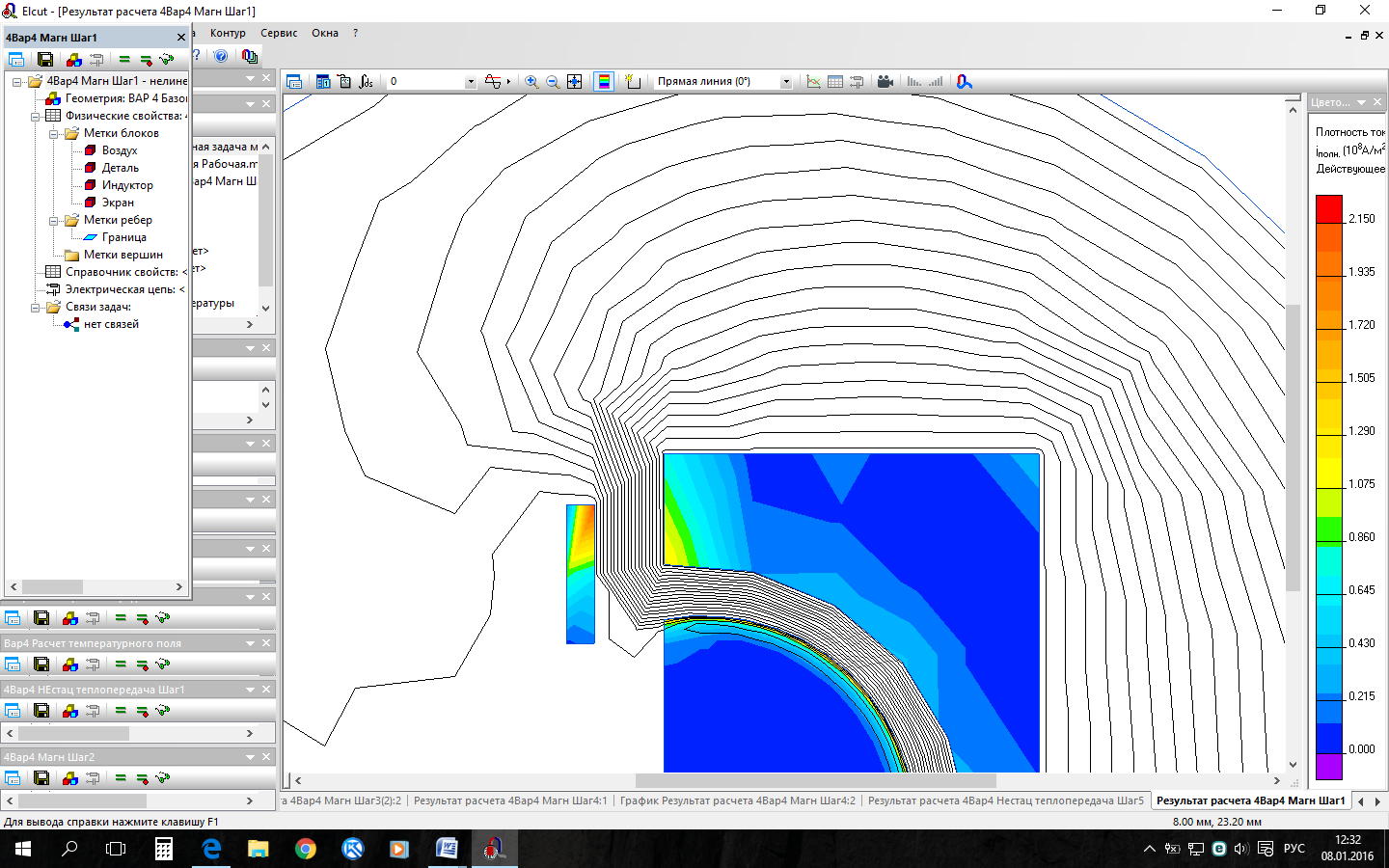 Рис.4 Картина плотности тока тепловыделения Заключение Входе выполнения курсовой работы было проведено моделирование индукционного нагрева с помощью программных средств по исходным данным проекта. Таким образом, поставленные на курсовое проектирование задачи выполнено в полном объеме. Библиографический список Исадченко, В.П. Теплопередача / В. П. Исадчеко [и др.] – М.: Энергоиздат, 1981. – 416 с. Вержбицкий, В.М. Основы численных методов: Учебник для вузов. - М.: Высш. шк., 2002. – 840 с. Зенкевич, О. Метод конечных элементов в технике / Пер. с англ. - М.: Мир, 1975. – 541с. Горбунов, В.А. Моделирование теплообмена в конечно-элементном пакете FEMLAB: Учеб. пособие / ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина». – Иваново, 2008. – 216 с. Бирюлин, Г.В. Теплофизические расчёты в конечно-элементарном пакете COMCOL/FEMLAB / Г. В. Бирюлин; СПбГУИТМО – С-Пб, 2006. – 76 с. Elcut. Моделирование двумерных полей методом конечных элементов / Руководство пользователя – Санкт-Петербург: Производственный кооператив ТОР, 2010. http://www.elcut.ru FlowVision. Система моделирования движения жидкости и газа. Руководство пользователя, ООО «Тесис», 2008. http://www.flowvision.ru Югов, В.П. Решение задач теплообмена / Москва: CADFEM, 2001. – 110 с. Инженерный анализ в ANSYS Workbench: Учеб. пособ. /В.А. Бруяка, В.Г. Фокин, Е.А. Солдусова, Н.А. Глазунова, И.Е. Адеянов. - Самара: Самар. гос. техн. ун-т, 2010. - 271 с.: ил. |
