творческая работа- моделирование ммногогранников. Творческая работа _Способы моделирования правильных многогранник. Моделирование правильных многогранников Модели многогранников из разверток

• Название: Моделирование правильных многогранников Модели многогранников из разверток
• Анкор: творческая работа- моделирование ммногогранников
• Дата: 06.03.2023
• Размер: 0.93 Mb.
• Имя файла: Творческая работа _Способы моделирования правильных многогранник.docx
• Тип: Документы; #972751

Моделирование правильных многогранников

1. Модели многогранников из разверток

Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

Чертеж развертки переносится на бумагу, дополняется небольшими выступами для склеивания. Вырезаем фигуру по контуру, сгибаем основным линиям. На выступы наносим клей и аккуратно склеиваем модель.



Рис. 49. Развертка тетраэдра



Рис. 50. Развертка октаэдра



Рис. 51. Развертка гексаэдра



Рис.52. Развертка икосаэдра



Рис. 53. Развертка додекаэдра

2. Каркасные модели многогранников

- Конструктор из гороха нут, размоченного в воде в течение 5-6 часов, и зубочисток – это отличный способ построить правильные многогранники.

Начнем наше конструирование с самого маленького многогранника – тетраэдра, всего он имеет 4 треугольные грани, которые являются равносторонними треугольниками и напоминает нам пирамиду (рис. 54). Что нам необходимо для сборки: 4 горошины – вершины и 6 ребер – зубочисток. В каждую вершину-горошину должно прийти 3 ребра, соединяем горошины зубочистками [41].



Рис. 54. Модель тетраэдра

Еще одна не очень сложная для сборки из конструктора фигура — это октаэдр (рис. 55) Если рассмотреть его половинку, то это пирамида с 4 гранями, которая похожа на Египетские пирамиды. Считаем сколько у октаэдра должно быть вершин и ребер: всего 6 вершин и 12 ребер. В каждую горошину-вершину должно подойти 4 ребра – зубочистки.



Рис. 55 Модель тетраэдра

Теперь приступим к сборке всеми любимого гексаэдра (рис. 56). Этот многогранник имеет 6 квадратных граней. Подсоединяем к вершинам нужное количество ребер, и наш куб готов.



Рис. 56. Модель куба

Сложный многогранник – додекаэдр (рис. 57), у которого 12 правильных пятиугольных граней. В каждую из 20 вершин-горошин нужно подсоединить по 3 ребра – зубочистки.



Рис. 57. Модель додекаэдра

А самый большой многогранник из нашей компании – икосаэдр (рис. 58), он состоит из 20 равносторонних треугольников. В идеале эта фигура похожа на футбольный мяч. В каждую из 12 вершин икосаэдра должно войти по 5 ребер. Собрать модель икосаэдра можно при помощи 20 тетраэдров.



Рис. 58. Модель додекаэдра
- Каркасные модели многогранников можно изготовить из трубочек.

Трубочки соединяются между собой леской[43;45].

В качестве примера рассмотрим инструкцию по сборке тетраэдра.

Таблица 7.Сборка тетраэдра из трубочек

1.	Наденьте на леску три трубочки.
2.	Проденьте один конец лески через крайнюю трубочку с другого конца.
3.	Затяните петлю, потянув за оба конца лески в разные стороны. Получится треугольник, тяните за более короткий конец, чтобы выровнять треугольник на середину лески.
4.	Добавьте на один из концов лески две новых трубочки, а затем второй конец проденьте через последнюю трубочку.
5.	Затяните леску, потянув за оба конца в разные стороны. Готов второй треугольник. Теперь проденьте леску как показано на рисунке.
6.	После этого возьмите последнюю шестую трубочку и проденьте в неё оба конца лески с разных сторон, и затяните третий треугольник.
7.	Остался последний четвёртый треугольник. Через четыре трубочки из шести леска проходит дважды, а через две другие – один раз. Проденьте каждый конец лески через одну ближайшую к нему трубочку, через которую леска проходит один раз. Оба конца должны выйти к одной вершине. Здесь нужно завязать узел. Теперь леска проходит дважды через каждую трубочку.
8.	Оба конца лески проденьте в одну из последних задействованных трубочек и слегка потяните за них, чтобы узел затянулся внутрь трубочки на пару миллиметров. Оставшуюся леску теперь можно обрезать. Тетраэдр готов.

3. Многогранник с помощью конструктора
Модели правильных многогранников можно изготовлять с помощью конструктора, состоящего из многоугольников, сделанных из плотного материала с отгибающимися клапанами и резиновых колечек – основной крепежной детали конструктора. Подбирая соответствующим образом многоугольники (рис. 59-61) в качестве граней многогранника и скрепляя их резиновыми колечками, можно получать модели различных правильных многогранников. Для того чтобы колечки лучше держались и не мешали друг другу, уголки многоугольников в конструкторе можно немного обрезать, как показано на рисунках.


Рис. 59 Рис. 60




Рис. 61

4. Многогранники из ленты

Математики давно уже доказали возможность построения трехмерных объектов из ленты. На рис. 62 показано, как получить тетраэдр, перегибая бумажную ленту по сторонам расчерченных на ней равносторонних треугольников.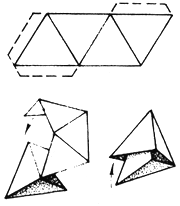



Рис. 62

Аналогичным способом можно свернуть куб (рис. 63). Его грани также выстраиваются в цепочку, а чтобы изменить направление ленты для завершения формообразования, достаточно перегнуть ее по диагонали квадрата .



Рис. 63

Так, ничем на первый взгляд не примечательная бумажная лента при нанесении на ее поверхность узора превращается в заготовку для построения самых разнообразных многогранников. На основе различных узоров можно создать все правильные многогранники, кроме додекаэдра. Это объясняется отсутствием у плоских узоров осей симметрии 5-го, 7-го и высших порядков – иначе говоря, сплошной узор из пятиугольников построить невозможно.



Рис. 64

Построение октаэдра (рис. 64) и икосаэдра (рис.65) осуществляется на основе узора из правильных треугольников. Свернув для октаэдра кольцо из шести, а для икосаэдра – из десяти треугольников, перегибаем ленту в обратную сторону и продолжаем сворачивать такие же кольца.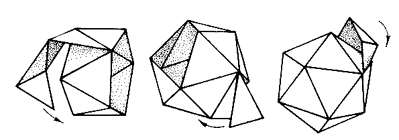



Рис. 65

Треугольные ячейки получаются наложением двух пар зеркальных гексагональных решеток, развернутых друг относительно друга на 90°, а квадратные – совмещением квадратных решеток под углом 45° друг к другу. С этих позиций процесс образования многогранников из фокуса превращается в теоретически обоснованное и закономерное явление.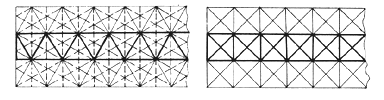



Рис. 66

В самом деле, когда сворачивается кольцо будущего многогранника, то в буквальном смысле производится перенос элементарной ячейки решетки на определенный шаг, то есть осуществляется переносная симметрия. Меняя направление формообразования за счет перегиба ленты в обратную сторону, производим мысленный поворот ячейки вокруг узла решетки, то есть проявляется уже симметрия поворотная. Стало быть, заготовка из ленты обеспечивает поворотно-переносную симметрию. Такая поворотно-переносная симметрия в наших построениях может осуществляться с углами поворотов; 30° 45°, 60°, 90°, 120°, 150°, 180°. В этом и состоит весь секрет способа образования из плоской ленты объемных тел.

Таким образом, ясно, что могут существовать только два типа лент с углами разбивки, кратными 30° и 45°. Из них получается четыре правильных многогранника: куб, октаэдр, тетраэдр, икосаэдр..

Лента имеет лицо и оборот, которые попеременно или одновременно участвуют в построении граней тела; каждый перегиб позволяет вести формообразование в двух направлениях. Отсюда нетрудно представить целое семейство игр-головоломок на основе ленты. Например, сложить рисунок, узор, орнамент, фрагменты которого разбросаны по ленте в заданном порядке.

5. Создание моделей правильных многогранников методами оригами.

Сегодня оригами переживает очередную волну интереса. Появились новые направления оригами и области его применения. Так, математики открыли множество возможностей для решения геометрических и топологических задач. Архитекторы и строители увидели в оригамном конструировании возможности для создания многогранных структур из плоского листа. Даже возник новый термин - "оригамика". Остановимся более подробно на создании моделей правильных многогранников методами оригами. Существует несколько методов оригами для создания одного и того же многогранника:

- Создание моделей правильных многогранников с помощью модуля Шеремет Г.Г. [10].

Этот модуль представляет собой правильный шестиугольник, который в результате перекладываний превращается либо в три равносторонних треугольника с двумя «вставками» и одним «карманом», либо в два равносторонних треугольника с двумя «карманами» и одной «вставкой».

Рис.67.

Схема сборки модуля Шеремета :

1. 
   Построение начинаем с правильного шестиугольника
   

2. 
   Наметить три линии сгиба, совмещающие стороны шестиугольника через одну с соответствующей диагональю
   

3. 
   Наметить средние линии получившегося правильного треугольника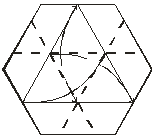
   

4. 
   Одновременно согнуть по всем указанным линиям
   

5 Заправить нижнюю полоску под слой бумаги

6. 
   Получилась фигура, составленная из трех равносторонних треугольников. Средний треугольник – основная часть. Одна сторона этого треугольника имеет удобный карман в форме равного ему треугольника. Два оставшихся треугольника играют роль вставок .
   

6. 
   Так как у треугольника нечетное число сторон, а при построениях желательно, чтобы число карманов и вставок совпадало, то второй вариант модуля получается из этого выворачиванием вовнутрь одного из треугольников-вставок
   

При желании, преобразуя этот модуль дальше, можно получить треугольный модуль с тремя карманами и без вставок.

- Создание моделей правильных многогранников из квадратного листа бумаги

Данные модели наименее трудоемкие и одни из самых простых в сборк.

Схема их сборки:



Итак,можно изготовить многогранник любого размера без всякой выкройки. Нужно только выбрать размер листа бумаги. /В этом мастер-классе показано, как строится модуль "Сонобе" и на его основе построен гексаэдр/



Для того, чтобы построить такой гексаэдр, необходимо сделать 6 одинаковых модулей. Модель интереснее будет, если просчитать цвета модулей.

Построение модуля "Сонобе". Согнуть квадратный лист бумаги пополам и четко выделить его осевую линию.



Развернуть согнутый лист и завернуть два противоположных конца к выделенной линии. Никаких отклонений не должно быть.

Один конец полученного прямоугольника согнуть к противоположной стороне. Выделить линию сгиба.



Аналогично поступить с противоположным концом. Получим параллелограмм. В этом параллелограмме необходимо получить еще две линии сгиба.

Вот такой модуль должен получиться. Параллелограмм, имеющий два кармана для соединения с другими параллелограммами. По сути здесь 4 кармана, но используются только два, те которые имеют продолжения.



Острый конец вставляем в карман.

Аналогично проделываем со всех сторон. Боковые стенки сделали. Остается тоже самое проделать снизу и сверху.

Получили гексаэдр без клея