Шалай, Трушляков, Куденцов_ж ТП в технике. Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет

• Название: Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет
• Дата: 09.12.2021
• Размер: 419 Kb.
• Имя файла: Шалай, Трушляков, Куденцов_ж ТП в технике.doc
• Тип: Документы; #297443

УДК 629.76

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ТЕПЛОМАССООБМЕНА ПРИ ГАЗИФИКАЦИИ ЖИДКИХ ОСТАТКОВ ТОПЛИВА В БАКАХ РАКЕТ
В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов^1*

Омский государственный технический университет, Омск, 644050, Россия
Проведено численное моделирование теплофизических параметров газовой фазы при проведении процесса газификации жидких остатков топлива в баках ракет. Установлены зависимости изменения коэффициента теплообмена в пристеночной области для различных режимов течения при изменении теплофизических параметров газовой фазы.

Ключевые слова: топливные баки, газификация, топливо, газовая фаза, тепломассообмен.
Введение

Для решения проблемы техногенного воздействия ракетно-космических комплексов на окружающую среду предложен подход на основе газификации жидких остатков компонентов ракетного топлива (КРТ) в топливных баках отделяющихся частей (ОЧ) ракет-носителей и разгонных блоков [1] Принципиальная схема системы газификации представлена на рис. 1.

Функционирование бортовых систем газификации жидких остатков КРТ происходит при следующих допущениях:

• 
  ограничение диапазона давления и температуры в объёме топливного бака ОЧ из условия термопрочностного нагружения конструкции;
  
• 
  максимальное сохранение химического состава газифицируемого КРТ с целью достижения высоких характеристик удельного импульса газового ракетного двигателя (ГРД).
  

Последнее допущение накладывает дополнительные требования на состав теплоносителя (ТН), допустимую концентрацию ТН в составе газифицированных КРТ, позволяющую реализовывать процесс химического взаимодействия в камере ГРД.

Сложность расчётного определения коэффициентов тепломассообмена заключается в изменении теплофизических параметров газовой фазы внутри топливных баков при проведении процесса газификации жидких остатков КРТ.

Целью данной работы является определение теплофизических параметров газовой фазы и оценка их влияния на коэффициенты тепломассообмена для различных жидких остатков КРТ при проведении процесса газификации в топливных баках ракет.

Постановка задачи

Рассматривалась осесимметричная задача с центральным вводом ТН в объём топливного бака. В качестве рассматриваемой топливной ёмкости принят бак, используемый на верхних ступенях ракет (с объёмом заправки до 7 м³).

Численное моделирование газодинамических потоков движения газовой фазы в объёме топливного бака проводилось с использованием программного комплекса ANSYS-CFX. При моделировании газодинамических потоков не учитывалось наличие внутрибаковых устройств (гасителей колебаний топлива, штанг систем контроля уровня, заборного устройства, тоннельного трубопровода и пр.) На рис. 2 представлены картины линий тока газовой фазы в объёме ёмкости. Анализ моделирования газодинамических потоков внутри ёмкости показал:

1. Осреднённые параметры скорости в пристеночной области топливного бака составляют:

• 
  около цилиндрической обечайки - 0,02÷0,06 от скорости ввода ТН в бак (U_тн), среднее значение - 0,05U_тн;
  
• 
  в районе нижнего днища: для центральной области, находящейся напротив ввода ТН – средняя скорость составляет 0,15U_тн, для остальной части 0,1U_тн;
  
• 
  в районе верхнего днища средняя скорость составляет 0,08U_тн.
  

2. Для центральной области нижнего днища, находящейся напротив ввода ТН, угол набегающего потока к поверхности близок к 90⁰, в остальной части ёмкости движение ТН вдоль стенки можно считать плоскопараллельным.

На рис. 3 представлена схема областей решения задачи.

При численном моделировании процесса газификации принимались следующие допущения:

1. 
   Остатки жидких КРТ на начало процесса газификации не превышают 3% от объёма ёмкости и равномерно распределены на внутренней поверхности топливного бака.
   
2. 
   Теплофизические параметры жидкого КРТ и материала стенки бака не зависят от температуры и определяются при начальных условиях процесса газификации.
   
3. 
   Прогрев плёнки жидкости и стенки бака равномерен.
   
4. 
   Волнообразование поверхности плёнки жидкости не учитывалось.
   
5. 
   Плёнка жидкого КРТ неподвижна относительно стенки ёмкости.
   
6. 
   Днища топливной ёмкости имеют экранно-вакуумную теплоизоляцию.
   
7. 
   Конденсация паровой фазы не учитывалась.
   
8. 
   Подвод тепла к жидкой пленке компонента топлива через стенку посредством теплопроводности не учитывался.
   
9. 
   Химическое взаимодействие между вводимым ТН и жидким остатком КРТ отсутствует.
   

Математическая модель и расчётные зависимости

Состав газовой фазы в объёме топливного бака при проведении процесса газификации жидких остатков КРТ будет определяться секундными расходами ТН, подаваемого в объём ёмкости, газифицированным КРТ и газом наддува, находящегося в объёме топливного бака до начала процесса газификации, используемого для вытеснения жидкого КРТ на активном участке траектории в камеры основного двигателя.

Уравнение изменения массы газовой фазы в объёме ёмкости за время процесса газификации: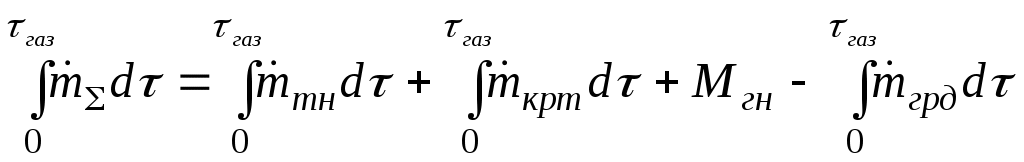

, (1)

Состав газовой смеси, поступающей в камеры ГРД, будет идентичен составу газа в свободном объёме ёмкости в процессе газификации.

Систему дифференциальных уравнений, описывающих термодинамический процесс газификации жидких остатков КРТ, с учётом уравнения (1) запишем в виде [2]: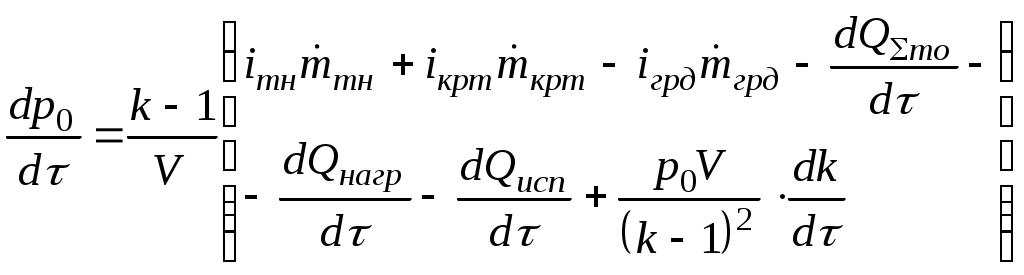

; (2)

; (3)

, (4)

Для оценки тепломассобмена при проведении процессов газификации жидких остатков КРТ в топливных баках ракет применим подход с использованием теории пограничного слоя на основе интегральных соотношений импульсов, энергии и диффузии. Согласно исследованиям [3], точное решение системы дифференциальных уравнений пограничного слоя возможно лишь для ограниченного круга задач. Использование интегральных соотношений позволяет получить удовлетворительные результаты при относительной простоте решения.

Учитывая высокую скорость натекания ТН (U₀=10÷80 м/с) на поверхность (L=0,5÷2,5 м), течение можно рассматривать как квазистационарное.

При проведении газификации жидких остатков КРТ в баке имеет место процесс испарения жидкости, равномерно распределённой на начало процесса по поверхности. Для данного условия стенка является проницаемой и от неё существует поперечный поток вещества, т.е. .

Система интегральных соотношений имеет следующий вид [3]:

• 
  уравнение импульсов
  

; (5)

• 
  уравнение энергии
  

; (6)

• 
  уравнение диффузии
  

, (7)

Температура жидкого КРТ определяется на основе следующего соотношения: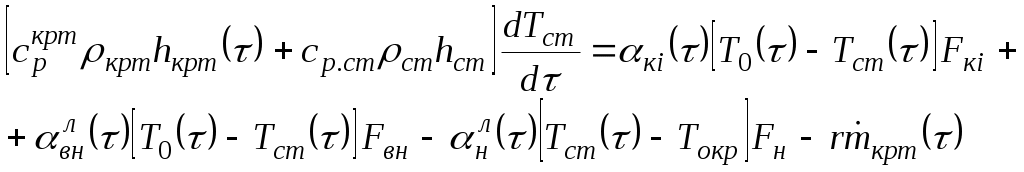

(8)

В уравнениях (1) – (8) приняты следующие обозначения [2,3]: , , , - соответственно массовые расходы и энтальпии вводимого ТН, газифицированного КРТ и газовой смеси, поступающей в камеру ГРД; М_гн - масса газа наддува топливного бака до момента начала процесса газификации; _газ- время процесса газификации; р₀, ρ₀,V,R,k - соответственно значения давления, плотности, объёма ёмкости, газовой постоянной продуктов газификации и показателя адиабаты процесса; Q_Σто - мощность потоков теплообмена продуктов газификации с жидким КРТ, элементами конструкции бака и внешней поверхности ёмкости с окружающей средой; Q_нагр - количество теплоты, расходуемая на нагрев КРТ и материала стенки топливного бака; Q_исп - количество теплоты, расходуемая на испарение жидкого КРТ; Re^**=ρ₀U₀δ^**/μ₀; ; ; Re_L=ρ₀U₀L/μ₀ - числа Рейнольдса, рассчитанные по динамическому, тепловому, диффузионному пограничному слою и по характерному размеру тела; St₀=q_ст/(ρ₀U₀c_pΔT)=α₀/(ρ₀U₀c_p), St_D0=j_ст/(ρ₀U₀ΔC) – соответственно числа Стентона (тепловое) и (диффузионное), полученные для «стандартных условий», т.е. для случая безградиентного обтекания поверхности несжимаемым газовым потоком с постоянной температурой и концентрацией вещества на стенке; - безразмерная координата; x – текущий размер; L – характерный линейный размер; H=δ^*/δ^** - формпараметр пограничного слоя; δ^* – толщина вытеснения; – толщина потери энергии; – толщина потери вещества; ΔT=T₀-T_ст, ΔС=С₀-С_ст - соответственно разность температур и массовых концентраций; с_p, U₀, μ₀, Т₀, С₀ – соответственно теплоёмкость, скорость, динамическая вязкость, температура и массовая концентрация для газового потока; Т_ст, С_ст – соответственно плотность, температура и массовая концентрация около поверхности; j_ст – поперечный поток вещества на проницаемой поверхности; с_f0– коэффициент сопротивления трения; ₀ - коэффициент теплоотдачи; Ψ_Σ=St/St₀ - относительная функция теплообмена и трения; b=2j_ст/(ρ₀U₀c_f0), b_Т=j_ст/(ρ₀U₀St₀), b_D=j_ст/(ρ₀U₀St_D0) - соответственно параметр проницаемости стенки, тепловой и диффузионный параметр; , , ρ_крт, ρ_ст, h_крт, h_ст – соответственно теплоёмкость, плотность и толщина пленки жидкого остатка КРТ и стенки бака; r - теплота испарения жидкого остатка КРТ; , F_кi – соответственно конвективный коэффициент теплоотдачи и площадь теплообмена для различных участков; , , F_вн, F_н – соответственно коэффициенты лучистого теплообмена и площади теплообмена внутренней полости и наружной поверхности топливного бака; Т_окр – температура окружающего пространства с наружной поверхности ёмкости.

Граничные условия для решения уравнений (5) – (7), с учётом расчётной схемы (рис.3):

Область 1. При x=0; U_ст=0; Т=Т_ст; при x=δ; U=U₀; Т=Т₀.

Область 2. При y=R_б; U_ст=0; Т=Т_ст; при y=R_б-δ; U=U₀; Т=Т₀.

Область 3. При x=L_б; U_ст=0; Т=Т_ст; при x=L_б-δ; U=U₀; Т=Т₀.

1) Определение теплофизических параметров газовой фазы

Теплоёмкость газовой фазы вычисляется по составу газовой смеси и теплоёмкостям отдельных её составляющих. Используя свойства аддитивности, определяем теплоёмкость газовой фазы

, (9)

где g_i, c_pi - соответственно весовые доли и теплоёмкости газов в газовой фазе. При этом .

Формула для расчёта теплоёмкости газовой фазы применительно для процесса газификации жидких остатков КРТ, с учётом (1) и (9), имеет вид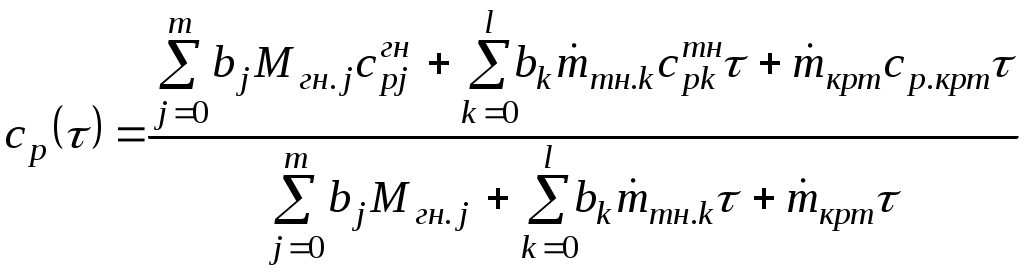

, (10)

где b_j. b_k – соответственно доли газов, входящих в состав газа наддува и вводимого ТН.

Отмечается, что теплофизические параметры компонентов газовой фазы определяются с использованием справочных данных, например [4-6]

Наибольшую сложность представляет собой выбор эмпирических зависимостей по расчёту коэффициентов теплопроводности и вязкости газовой смеси. В настоящее время на основе теоретико-экспериментальных исследований выведены эмпирические зависимости, имеющие свои погрешности расчёта и адаптированные к определённым составам газовой смеси.

Для газовой фазы, в составе которой находятся компоненты, имеющие малую молекулярную массу (в качестве газа наддува используется гелий), при расчёте коэффициента теплопроводности можно рекомендовать формулу Лемана [7]:

, (11)

где χ_i, , М_ri – соответственно мольная моля, коэффициент теплопроводности при температуре газификации и молекулярная масса i-го компонента в составе газовой фазы.

Для инженерных расчётов коэффициента теплопроводности компонентов газовой фазы при температуре процесса газификации воспользуемся формулой Сатерленда [7]

, (12)

где ⁰ - коэффициент теплопроводности при 0⁰C; С – постоянная Сатерленда.

Постоянная С определяется по зависимости , где Т_кип - температура кипения компонента газовой смеси.

Формула расчёта коэффициента теплопроводности газовой фазы, с учётом (1), (11), (12) имеет вид

,(13)

Для технических расчётов вязкости газовой фазы, содержащие компоненты, имеющие малые молекулярные массы (например, гелий), можно рекомендовать формулу Хеннинга и Ципперера [7]

, (14)

где x_i, - объёмная доля и вязкость компонентов газовой фазы при температуре газификации.

Для расчёта вязкости компонентов газовой фазы при температуре протекания процесса газификации остатков КРТ воспользуемся формулой Сатерленда [7]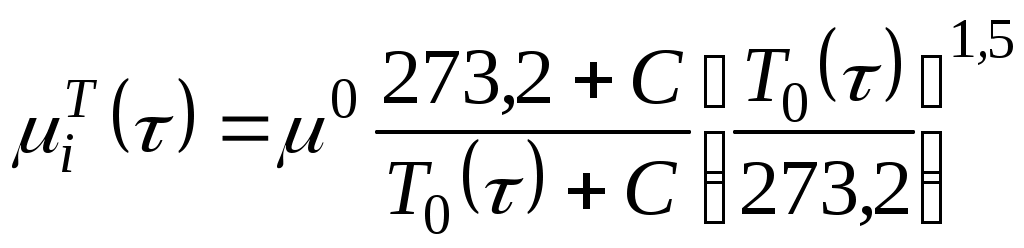

, (15)

где ⁰ - вязкость компонента газовой фазы при 0⁰C.

Постоянная С определяется по зависимости .

С учётом (1), (14), (15) вязкость газовой фазы определяется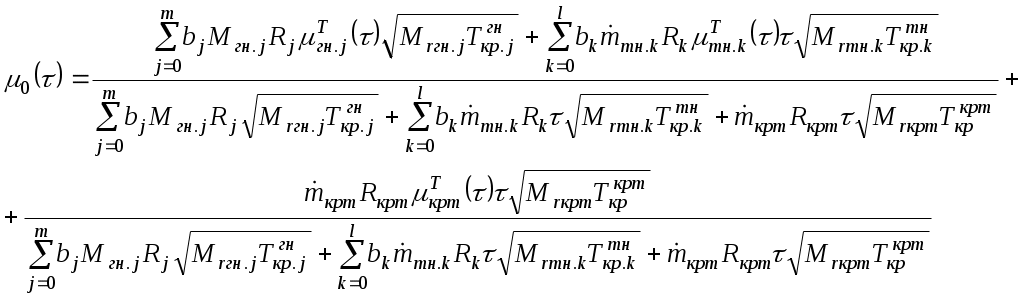

, (16)

где R_j, R_k, R_крт – соответственно газовые постоянные компонентов газовой фазы.

2) Определение коэффициента тепломассообмена при ламинарном режиме течения.

Отмечается, что в инженерных расчётах принимают, что переход от ламинарного пограничного слоя к турбулентному на плоской пластине происходит в диапазоне (Re_x)_кр=(2÷5)·10⁵. Согласно данным [3] переходная область наблюдается при (Re_x)_кр=3,2·10⁵.

Исследования [8] показали, что неизотермичность потока слабо влияет на законы трения и теплообмена для ламинарного пограничного слоя. При проведении газификации жидких остатков КРТ коэффициент неизотермичности потока равен ψ=0,84÷0,89. В этих условиях, при малых скоростях течения ТН М<1, влияние изменения теплофизических свойств может взаимно компенсироваться и в дальнейших расчётах неизотермичностью потока можно пренебречь.

Для ламинарного пограничного слоя закон теплообмена в стандартных условиях [3] при изменяющихся теплофизических параметрах газовой фазы определяется

, (17)

где Pr(τ)=μ₀(τ)c_p(τ)/λ₀(τ) - число Прандтля.

Относительный закон теплообмена определяем, используя плёночную модель течения ТН на проницаемой поверхности 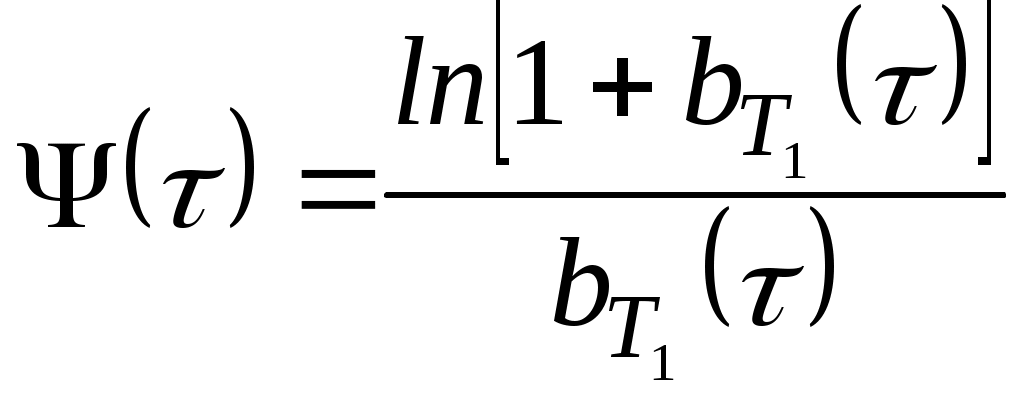[8]

, (18)

где b_T1(τ)=1/K(τ), – критерий Кутателадзе.

Число Рейнольдса, рассчитанное по тепловому пограничному слою, определяется по следующей формуле [8]

, (19)

где Re_x(τ)=ρ₀(τ)U₀x/μ₀(τ) - число Рейнольдса, определяемое по координате x.

Параметр проницаемости стенки b_Т определяется b_T(τ)=Ψ(τ)/K(τ).

С учётом формул (17) – (19) число Стентона при плоском течении ТН

. (20)

Коэффициент теплоотдачи, с учётом зависимостей (10), (13), (16) и (20), для ламинарного пограничного слоя при плоскопараллельном течении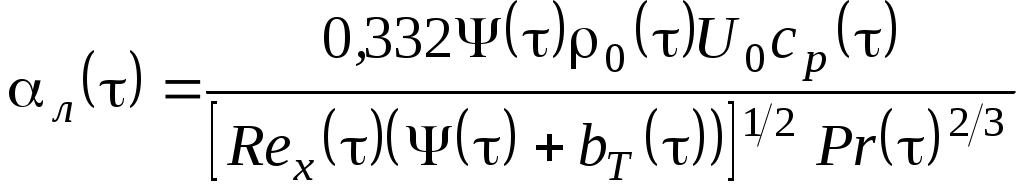

. (21)

Выражение для определения среднего значения коэффициента теплоотдачи в районе нижнего днища при угле натекания ТН близкого к 90⁰ [8], с учётом зависимости (21) имеет вид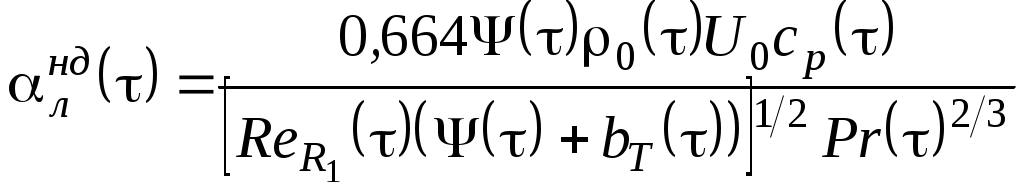

. (22)

Радиус площади теплообмена при угле натекания ТН близкого к 90⁰ составляет R₁=(0,1÷0,15)R_б.

3) Определение коэффициента тепломассообмена при турбулентном режиме течения.

Для расчёта интегральных соотношений примем степенной профиль скорости. В диапазоне изменения Prот 0,5 до 10 хорошие результаты даёт следующее соотношение [9]:

.

Коэффициент А и показатель степени m определяются в зависимости от степени профиля скорости на поверхности. Согласно [9] для диапазона чисел Рейнольдса , коэффициент А=0,0128, показатель степени m=0,25.

Коэффициент теплоотдачи при наличии неизотермичности потока ТН на проницаемой поверхности определяется

, (23)

где Ψ_Т()– параметр неизотермичности потока ТН; Ψ_b() – функция, учитывающая проницаемость поверхности.

Принимая допущения, что расчёт турбулентного пограничного слоя начинается сразу после ламинарного участка, U₀=const, число Рейнольдса, рассчитанное по тепловому пограничному слою, определяется по следующей формуле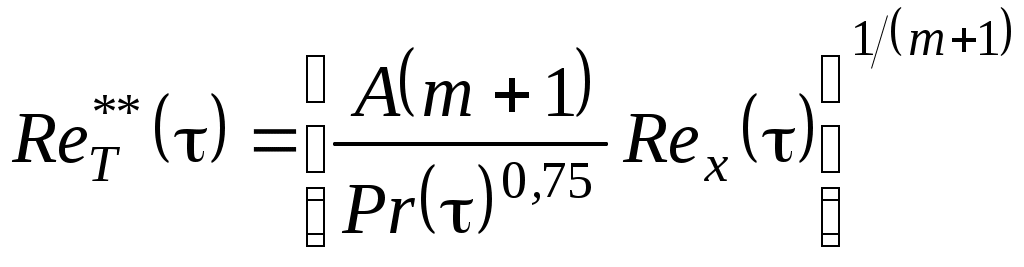

. (24)

Для принятого степенного профиля скорости, формула (24) преобразуется к следующему виду

. (25)

Параметр неизотермичности потока

, (26)

где ψ(τ)=Т_ст(τ)/Т₀(τ) – температурный фактор.

Функция, учитывающая проницаемость поверхности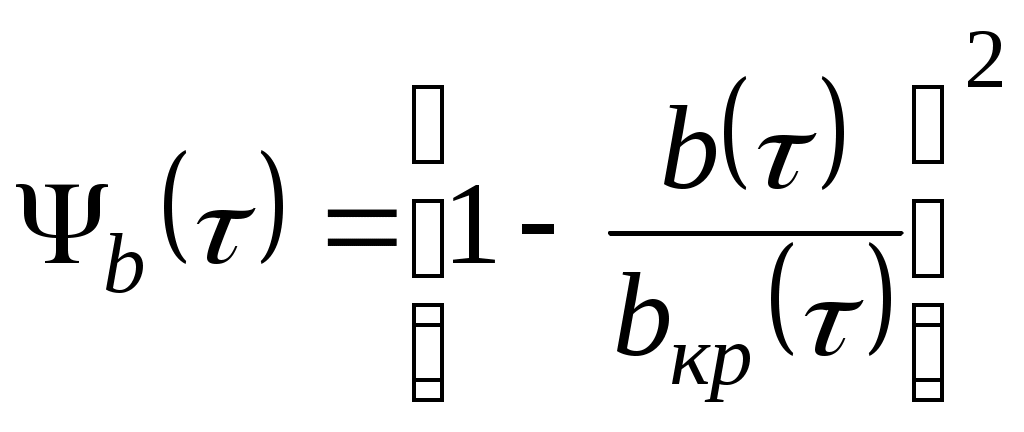

, (27)

где b_кр() – критический параметр вдува, определяемый по следующей формуле:

при ψ(τ)<1 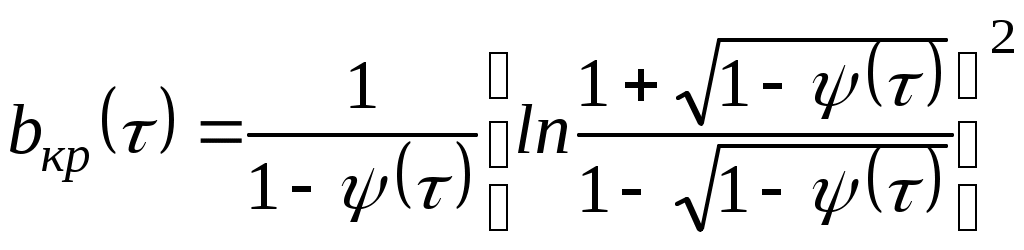. (28)

Параметр проницаемости находится по следующей формуле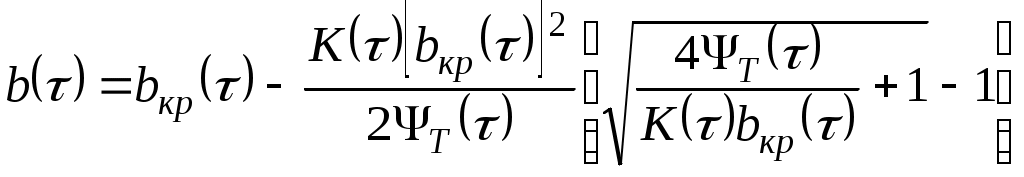

. (29)

С учётом формул (10), (13), (16), (23) – (29) коэффициент теплоотдачи для турбулентного пограничного слоя определяется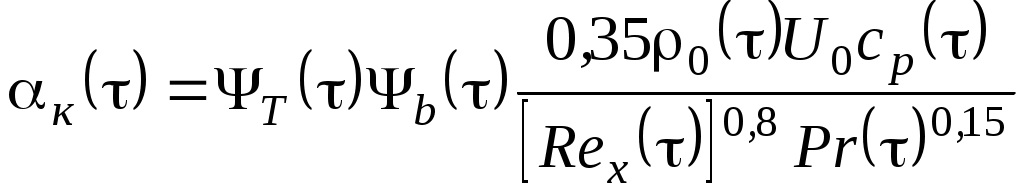

. (30)

Результаты и обсуждение

Проведём оценку изменения теплофизических параметров газовой фазы в топливных баках на примере топливных пар, используемых в отечественном ракетостроении: кислород (ж.), керосин, азотный тетраксид (АТ), несимметричный диметилгидразин (НДМГ). В качестве газа наддува используется газообразный гелий. Процесс газификации протекает без химического взаимодействия между вводимым ТН и жидким остатком топлива. Состав ТН содержит следующие компоненты: для бака с НДМГ (СО₂, СО, Н₂О, СН₄, С₂H₄, Н₂, NH₃, HCN, C₂H₈N₂, CH₃NH₃, C_тв) [2]; для бака с АТ (СО₂, Н₂О, N₂, O₂, NO₂, NO) [3]; для бака с керосином (СО₂, Н₂О, керосин (парообразная фаза); для бака с кислородом (ж.) (О₂, Н₂О). На начало процесса газификации доля газообразного КРТ составляет до 20% по массе в составе газа наддува.

Параметры процесса газификации: Для всех баков принято максимальное давление в ёмкости р_б=2,7·10⁵ Па; рабочая температура протекания процесса газификации жидких остатков КРТ различна и составляет: для бака с кислородом (ж.) (Т_кис=220 К); для бака с керосином (Т_кер=380 К); для бака с АТ (Т_ат=332 К); для бака с НДМГ (Т_ндмг=353 К) [4] Начальные температуры жидких остатков КРТ: для бака с кислородом (ж.) (Т_кис=83 К); для бака с керосином, АТ и НДМГ (Т₀=290 К). Температура окружающей среды Т_нар=12 К. Начальная скорость ввода ТН U_тн=500 м/с. Начальное давление в топливных баках р_0нач=1,5·10⁵ Па.

По окончании процесса газификации массовый состав газовой фазы (ТН/газ наддува/газифицированный КРТ) в соответствии с формулой (1) составил: для бака с кислородом (ж.) (0,07/0,09/0,84); для бака с керосином (0,14/0,08/0,78); для бака с АТ (0,32/0,04/0,64); для бака с НДМГ (0,46/0,03/0,51) [10]

На рис. 4 представлен график изменения теплоёмкости газовой фазы по времени процесса газификации (здесь и далее - относительное время). Теплоёмкость газовой фазы в начальный момент времени определяется параметрами газовой подушки, где доминирующим компонентом является гелий, имеющий высокую теплоёмкость. Теплоёмкость газовой фазы к концу процесса уменьшается на 71% - для бака с кислородом (ж.), на 51% - для бака с керосином, на 75% - для бака с АТ и на 64% - для бака с НДМГ от первоначального значения. Отмечается, что с момента времени показатель теплоёмкости для бака с НДМГ стабилизируется.

На рис. 5 представлен график изменения коэффициента теплопроводности газовой фазы по времени процесса газификации. Коэффициент теплопроводности газовой фазы к концу процесса уменьшается на 74% - для бака с кислородом (ж.), на 78% - для баков с керосином и НДМГ и на 84% для бака с АТ от первоначального значения.

На рис. 6 представлен график изменения вязкости газовой фазы по времени процесса газификации. Изменение вязкости газовой фазы носит сложный характер, определяемый содержанием в газовой фазе составляющих ТН и газифицированного жидкого остатка КРТ. Вязкость газовой фазы к концу процесса уменьшается на 2% - для бака с кислородом (ж.), на 51% - для бака с керосином, на 19% - для бака с АТ и на 25% - для бака с НДМГ от первоначального значения.

На рис. 7 представлен график изменения относительного коэффициента теплоотдачи для ламинарного режима течения по времени процесса газификации. На рис. 7 параметр - относительный коэффициент теплоотдачи, где – текущее значение коэффициента теплоотдачи; _л.нач – коэффициент теплоотдачи в начальный период процесса. Коэффициент теплоотдачи для ламинарного режима течения в пристеночной области к концу процесса уменьшается на 73% - для бака с кислородом (ж.), на 68% - для бака с керосином, на 80% - для бака с АТ и на 72% - для бака с НДМГ от первоначального значения.

На рис. 8 представлен график изменения относительного коэффициента теплоотдачи для турбулентного режима течения по времени процесса газификации. На рис. 8 параметр - относительный коэффициент теплоотдачи, где – текущее значение коэффициента теплоотдачи; _т.нач – коэффициент теплоотдачи в начальный период процесса. Коэффициент теплоотдачи для турбулентного режима течения в пристеночной области к концу процесса уменьшается на 73% - для бака с кислородом (ж.), на 60% - для бака с керосином, на 79% - для бака с АТ и на 69% - для бака с НДМГ от первоначального значения.

Заключение

Численное моделирование теплофизических параметров газовой фазы при проведении газификации жидких остатков КРТ в топливных баках ракет позволило определить качественную картину процесса. Установлены зависимости коэффициента теплообмена в пристеночной области для различных режимов течения с учётом изменения теплофизических параметров газовой фазы.

Полученные результаты теоретического исследования рекомендуются к использованию для расчёта процессов тепломасообмена при газификации жидких остатков КРТ в топливных баках ракет.

Список литературы

1. 
   Наукоёмкие технологии в технике: энциклопедия: Т. 28 / Под общ. ред. А.Н. Котова; А.Н. Котов и др. – М.: ЗАО «НИИ «ЭНЦИТЕХ», 2010. – 383 с.
   
2. 
   Беляев Н.М. Системы наддува топливных баков ракет / Н.М. Беляев. – М.: Машиностроение, 1976. – 336 с.
   
3. 
   Теория тепломассообмена: Учебник для вузов / С.И. Исаев, И.А. Кожинов, В.И. Кофанов и др.; Под ред. А.И. Леонтьева. – М.: Высш. школа, 1979. – 495 с.
   
4. 
   Греков А.П. Физическая химия гидразина / А.П. Греков, В.Я. Веселов. – Киев: Наукова думка, 1979. – 254 с.
   
5. 
   Термодинамические свойства индивидуальных веществ: Справочник: Т. I.: Кн. 2. / Л.В. Гурвич и др. – М.: Наука, 1978. – 328 с.
   
6. 
   Физические величины: Справочник / А.П. Бабичев и др.; под. ред. И.С. Григорьева, Е.3. Мейлихова. - М.: Энергоатомиздат, 1991. – 1232 с.
   
7. 
   Бретшнайдер С. Свойства газов и жидкостей. Инженерные методы расчёта / С. Бретшнайдер. – М., Л.: Химия, 1966. – 535 с.
   
8. 
   Волчков Э.П. Тепломассообмен в пристенных течениях: Учебник / Э.П. Волчков, В.П. Лебедев. – Новосибирск: Изд-во НГТУ, 2003. – 244 с.
   
9. 
   Кутателадзе С.С. Тепломассообмен и трение в турбулентном пограничном слое. / С.С. Кутателадзе, А.И. Леонтьев. – М.: Энергоатомиздат, 1985. – 320 с.
   
10. 
    Трушляков В.И. Разработка критериев для оценки параметров процесса газификации жидкого ракетного топлива в условиях малой гравитации / В.И. Трушляков, В.Ю. Куденцов // Омский научный вестник. – 2010. – №2 (90). – С. 97-100.
    

Подписи к рисункам
Рисунок 1 - принципиальная схема системы газификации жидких остатков топлива: 1 - шар-баллон с нейтральным газом; 2 - вытеснительная ёмкость с окислителем; 3 – газогенератор; 4 - вытеснительная ёмкость с горючим; 5 – сопла газового ракетного двигателя; 6 - приводы сопел; 7 – смесительный коллектор.

Рисунок 2 - картины линий тока газовой фазы в объёме топливного бака для различных плоскостей (а – в плоскости I-III; б – в плоскости II-IV).

Рисунок 3 – схема области решения задачи: 1 – нижнее днище; 2 – цилиндрическая обечайка бака; 3 – верхнее днище.

Рисунок 4 - график изменения теплоёмкости газовой фазы по времени процесса газификации.

Рисунок 5 - график изменения коэффициента теплопроводности газовой фазы по времени процесса газификации.

Рисунок 6 - график изменения вязкости газовой фазы по времени процесса газификации.

Рисунок. 7 - график изменения относительного коэффициента теплоотдачи для ламинарного режима течения по времени процесса газификации.

Рисунок 8 - график изменения относительного коэффициента теплоотдачи для турбулентного режима течения по времени процесса газификации.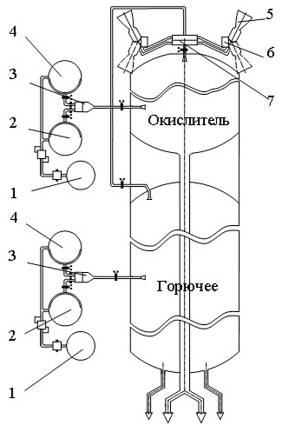





Рис. 1

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет



Рис. 2

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет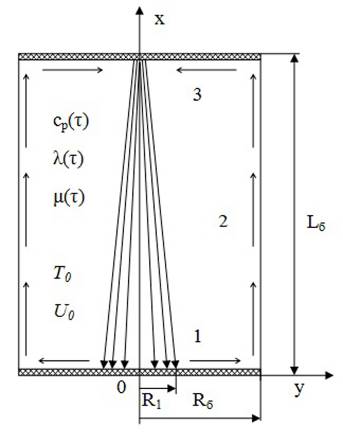



Рис. 3

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет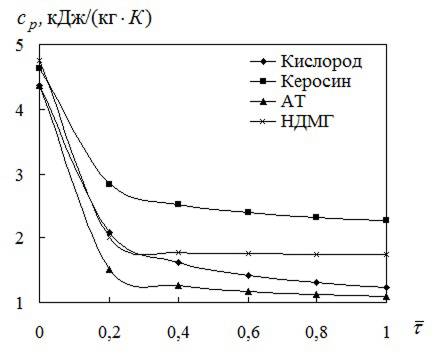



Рис. 4

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет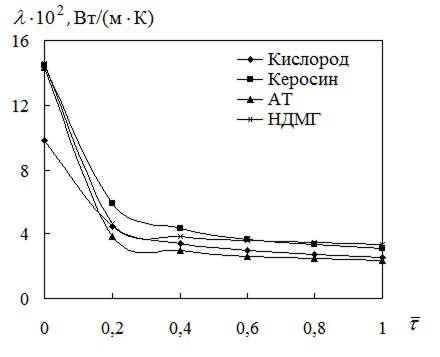



Рис. 5

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет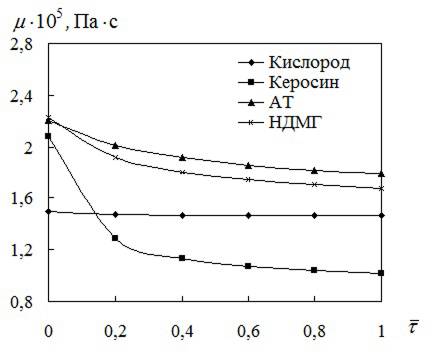



Рис. 6

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет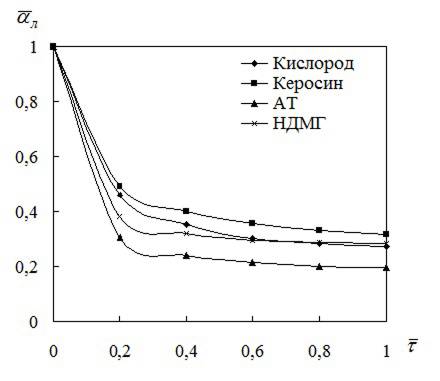



Рис. 7

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет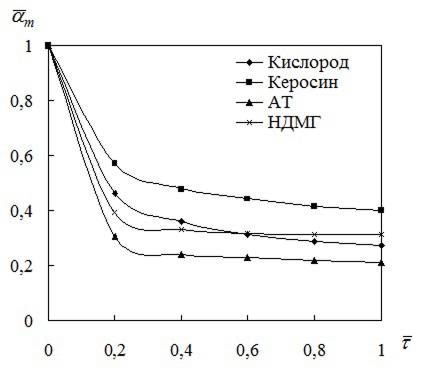



Рис. 8

В.В. Шалай, В.И. Трушляков, В.Ю. Куденцов

Моделирование процессов тепломассообмена при газификации жидких остатков топлива в баках ракет

Simulation process of heat and mass transfer in gasification of liquid remaining fuel in the tanks rockets
V.V. Shalai, V.I. Trushlyakov, V.J. Kudentsov

Omsk state technical university, Omsk, 644050, Russia
Numerical modeling of thermophysical parameters of a gas phase when carrying out process of gasification of the liquid remains of fuel in tanks of rockets. Dependences of change of coefficient of heat exchange in wall region for various modes of a current are established at change of thermophysical parameters of a gas phase.

Keywords: fuel tanks, gasification, fuel, gas phase, heat and mass transfer.

1Куденцов Владимир Юрьевич, e-mail: [e-mail], т. [phone], моб. [phone]