Моделирование аппарата идеального перемешивания. ПР 1. Моделирование работы аппарата с перемешивающим устройством. Моделирование работы аппарата с перемешивающим устройством
 Скачать 102.24 Kb. Скачать 102.24 Kb.
|
|
Практическая работа 1 Тема: Моделирование работы аппарата с перемешивающим устройством Цели работы: ознакомиться с моделью идеального перемешивания (ИП); научиться определять среднее время пребывания потока в аппарате по экспериментальной функции отклика на импульсное возмущение; освоить практическое применение модели ИП для исследования работы аппарата с мешалкой; решить приведенную задачу. Краткие теоретические сведения Модель ИП является теоретической моделью с идеализированной структурой потока. В соответствии с ней принимается, что поступающий в аппарат поток вследствие полного перемешивания частиц среды мгновенно распределяется по всему объему. При этом концентрация распределенного вещества во всех точках аппарата одинакова и равна концентрации на выходе. Схематично данную модель можно представить следующим образом:   . .Модель ИП наиболее адекватно воспроизводит структуру потока в аппаратах с мешалками (рис. 1), имеющими эллиптические или полусферические днища, соотношение высоты и диаметра корпуса, близкое к единице, снабженные отражательными перегородками. Математическое описание модели ИП имеет вид
где  – среднее время пребывания потока в аппарате; – среднее время пребывания потока в аппарате;  – объёмный расход потока; Va – объём аппарата. Свх, С и Свых – концентрация вещества на входе в аппарат, в аппарате и на выходе из аппарата соответственно. – объёмный расход потока; Va – объём аппарата. Свх, С и Свых – концентрация вещества на входе в аппарат, в аппарате и на выходе из аппарата соответственно. В условиях стационарного режима и отсутствия каких-либо превращений вещества Свх = С = Свых. Отклики модели на типовые возмущения представлены на рис. 2.   Рис. 1. Принципиальная схема аппарата с мешалкой  t, минt, мин  Рис. 2. Отклики модели ИП на типовые возмущения Решения модели: Импульсное возмущение Для граничных условий Свх= 0 и Свых= Сн = G/Va в момент времени t = 0,
где t – текущее время; Сн – начальная концентрация индикатора в потоке в момент времени t = 0; G – масса индикатора, введенного в аппарат. Основным параметром модели ИП является среднее время пребывания  , которое в случае импульсного возмущения определяется по формуле , которое в случае импульсного возмущения определяется по формуле
где 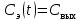 – экспериментальное значение функции отклика. – экспериментальное значение функции отклика.Использование полученной функции отклика в натуральных значениях координат Сэ(t) – t не всегда является удобным для расчетов, поэтому кривую отклика обычно приводят к безразмерному виду С(θ) – θ и называют С-кривой. Здесь θ– безразмерное время, равное 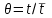 , а С(θ) – безразмерная концентрация, равная , а С(θ) – безразмерная концентрация, равная  , где , где 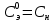 . Безразмерная концентрация связана со средним временем пребывания и экспериментальным значением функции отклика . Безразмерная концентрация связана со средним временем пребывания и экспериментальным значением функции отклика  следующей зависимостью: следующей зависимостью:
где выражение
задает нормированную кривую отклика. Таким образом, С-кривая является характеристикой распределения элементов потока по времени их пребывания в аппарате. При практическом определении среднего времени пребывания по экспериментальной С-кривой знаки интегралов в выражении (4) заменяются на знаки суммы и посредством суммирования (см. приложение к ПР 1) определяется  . .ЗАДАНИЕ Ознакомиться с кратким изложением теории. По результатам испытания аппарата импульсным методом (табл. 1) определить среднее время пребывания потока в аппарате (см. приложение к ПР 1) и построить кривую отклика в безразмерных координатах С(θ) – θ . Таблица 1 Результаты испытания аппарата импульсным методом
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 или
или  ,
, , (2)
, (2) , (4)
, (4) , (5)
, (5) (6)
(6)