васильев. Модуль 1. Физикомеханические свойства материалов бетонных и железобетонных конструкций. Сущность железобетона

• Название: Модуль 1. Физикомеханические свойства материалов бетонных и железобетонных конструкций. Сущность железобетона
• Анкор: васильев.doc
• Дата: 25.12.2017
• Размер: 24.66 Mb.
• Имя файла: васильев.doc
• Тип: Документы; #12933
• страница: 3 из 5

10.2.Расчет по прочности нормальных сечений с двойной арматурой.

В практике проектирования часто встречаются случаи двойного армирования, т.е. установки в сжатую зону арматуры, хотя она там используется менее эффективно. Это производится в случаях для одиночного армирования при - низкая прочность бетона, недостаточная высота сечения. При этом сжатую арматуру должна раскреплять поперечная арматура.

Расчет прямоугольных сечений (рис.10.2) производится следующим образом в зависимости от высоты сжатой зоны

(10.1)

а) при - из условия

M < R_bbх(h₀ – 0,5x) + (h₀– a’); (10.2)

б) при  > _R – из условия

M < _RR_bbh+ (h₀ - a'), (10.3)

где _R =_R(1 – 0,5_R).

Если прочность проверяют из условия

MR_sA_s(h₀ – a'). (10.4)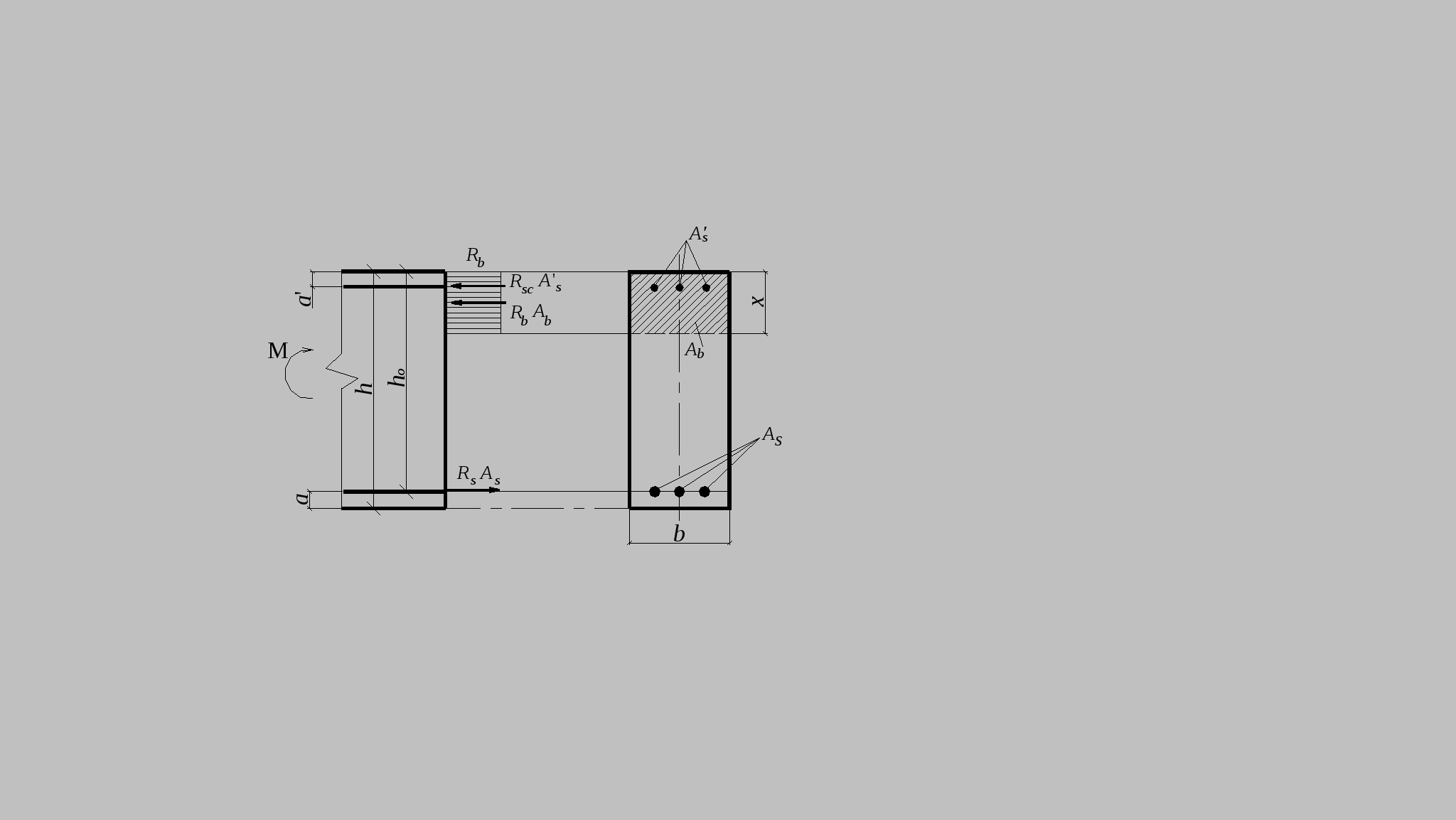


Рис.10.2. Схема усилий и эпюра напряжений в поперечном прямоугольном сечении изгибаемого железобетонного элемента с двойным армированием
Изгибаемые элементы рекомендуется проектировать так, чтобы обеспечить выполнение условия  ≤ _R. Невыполнение этого условия можно допустить лишь в случаях, когда площадь сечения растянутой арматуры определена из расчета по предельным состояниям второй группы или принята по конструктивным соображениям.

Задача 1 типа. Определить площади сечения растянутой A_sи сжатой арматуры, соответствующие минимуму их суммы.

Учитывая, что площадь арматуры определяют по формулам:

(10.5)

A_s = _RR_bbh₀/R_s + , (10.6)

где _R и_R – определяются по зависимостям(см.формулу 3) .

Задача второго типа. Заданы размеры сечения b и h и площадь сжатой арматуры . Тре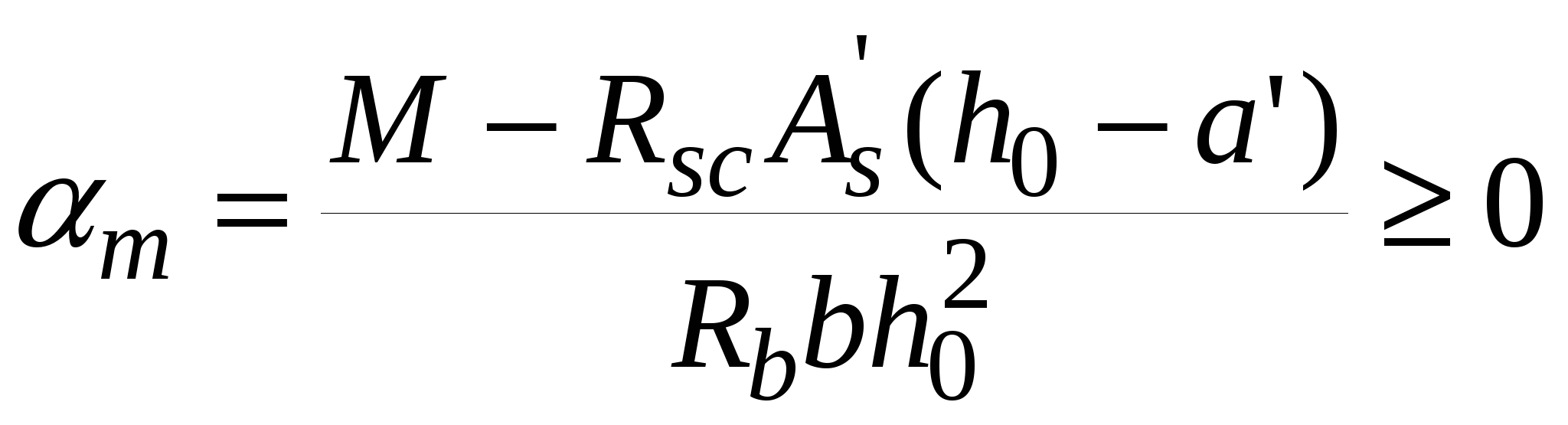буется определить площадь сечения растянутой арматуры. Определяют параметр

, (10.7)

.

Если _m < _Rто площадь растянутой арматуры определится

.

Если _m > _R то сжатой арматуры недостаточно.
10.3.Тавровые и двутавровые сечения

Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и т.п.), производят в зависимости от положения границы сжатой зоны:

а) если граница проходит в полке (рис.10.3,а), т.е. соблюдается условие

R_sA_sR_b, (10.8)

расчет производят как для прямоугольного сечения шириной ;

б) если граница проходит в ребре (рис.10.3,б), т.е. условие (10.8) не соблюдается, расчет производят из условия: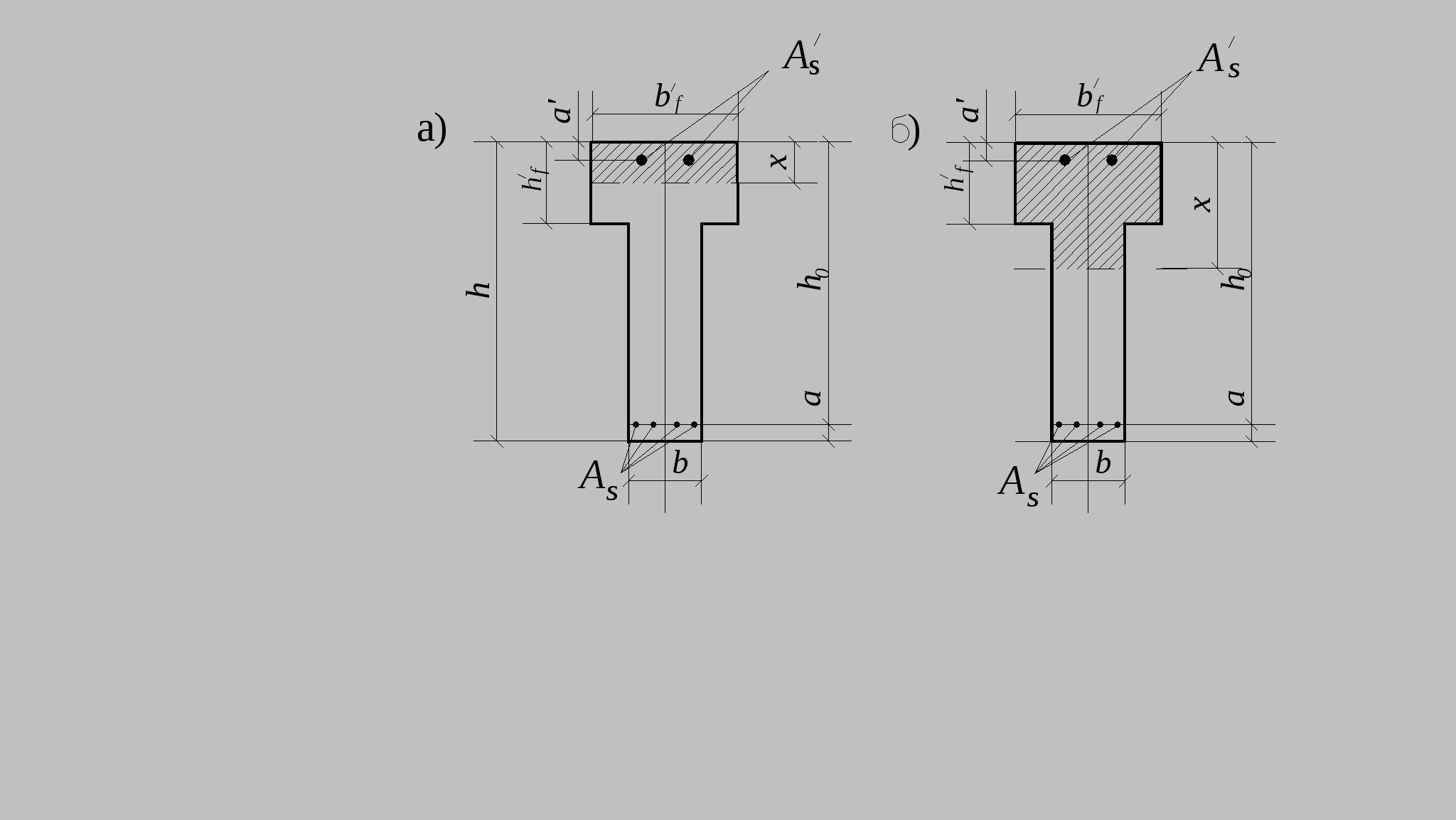



Рис.10.3. Положение границы сжатой зоны в тавровом сечении изгибаемого железобетонного элемента

а - в полке; б - в ребре
, (10.9)

при этом высоту сжатой зоны определяют по формуле

, (10.10)

и принимают не более _Rh₀ .

Если x >_Rh₀, условие (9) можно записать в виде

. (10.11)

Примечания: 1. При переменной высоте свесов полки допускается принимать значение , равным средней высоте свесов.

2. Ширина сжатой полки , вводимая в расчет, не должна превышать величин: при отсутствии поперечных ребер (или при расстояниях между ними, больших, чем расстояния между продольными ребрами) и при

в) при консольных свесах полки

при -

при

при - свесы не учитывают.
Требуемую площадь сечения сжатой арматуры определяют по формуле

, (10.12)

где A_ov = .

При этом должно выполняться условие . В случае, если , площадь сечения сжатой арматуры определяют как для прямоугольного сечения шириной по формуле (10.5).

Требуемую площадь сечения растянутой арматуры определяют следующим образом:

а) если граница сжатой зоны проходит в полке, т.е. соблюдается условие:

(10.13)

площадь сечения растянутой арматуры определяют как для прямоугольного сечения шириной ;

б) если граница сжатой зоны проходит в ребре, т.е. условие (10.13) не соблюдается, площадь сечения растянутой арматуры определяют по формуле

, (10.1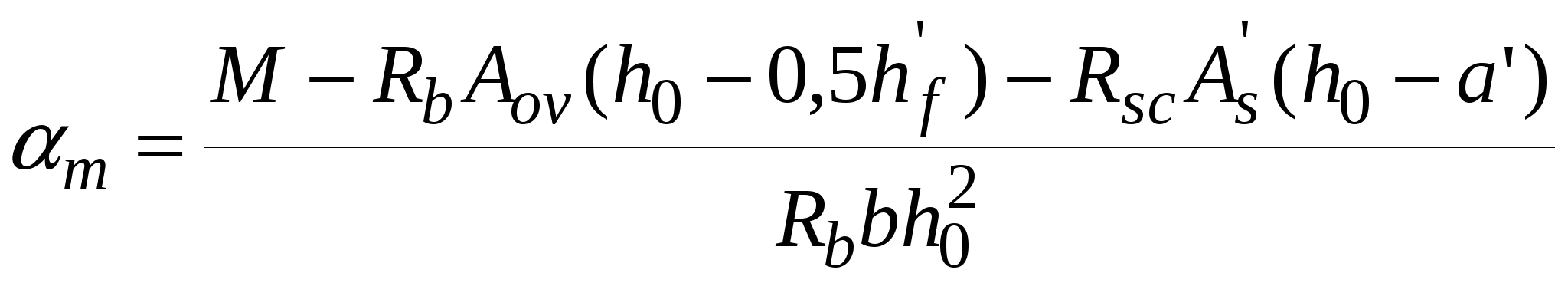4)

где .

11.Прочность изгибаемых железобетонных элементов по наклонным сечениям

На приопорных участках изгибаемых элементов действуют поперечные силы Q и изгибающие моменты M. Главные растягивающие и главные сжимающие напряжения действуют под углом к продольной оси. Поэтому расчет по прочности при действии поперечных сил производят на основе модели наклонных сечений.

В сечениях наклонных к продольной оси элемента прослеживаются три стадии НДС. Если главные растягивающие напряжения превысят R_bt то появляются наклонные трещины. Усилия передаются на продольную и поперечную арматуру. Разрушение происходит вследствие раздробления бетона в вершине наклонной трещины и достижения в поперечной арматуре предельных напряжений или продергивания продольной арматуры (в продольной арматуре напряжения, как правило, не достигают предельных).

Расчет элементов при действии поперечных сил должен обеспечить прочность:

- по сжатой бетонной полосе между наклонными сечениями;

- на действие поперечной силы по наклонному сечению;

- на действие момента по наклонному сечению.
Расчет железобетонных элементов по сжатой полосе между наклонными сечениями. Если главные сжимающие напряжения в бетоне превысят R_b то произойдет разрушение бетона по наклонной полосе. Поэтому расчет изгибаемых элементов по бетонной полосе между наклонными сечениями производят из условия

Q  0,3R_bbh₀, (11.1)

гдеQ – поперечная сила в нормальном сечении, принимаемая на расстоянии от опоры не менее h₀.

Проверку производят при учащенном поперечном армировании и тонкой стенке балки (например, балки покрытия).
Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил. Расчет изгибаемых элементов по наклонному сечению (рис.11.1) производят из условия

QQ_b + Q_sw, (11.2)

где Q– поперечная сила в наклонном сечении с длиной проекции с от внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при вертикальной нагрузке, приложенной к верхней грани элемента.

Значение Q принимается в нормальном сечении, проходящем на расстоянии с от опоры;

Q_b – поперечная сила, воспринимаемая бетоном в наклонном сечении;

Q_sw – поперечная сила, воспринимаемая хомутами в наклонном сечении.

Поперечную силу Q_b определяют по формуле

(11.3)

где M_b= _b2 R_btb .(11.4)

здесь _b2 =1.5.

Значение Q_b принимают не более 2,5R_btbh₀ и не менее 0,5R_btbh₀.

При проверке условия (11.2) в общем случае задаются рядом наклонных сечений при различных значениях с, не превышающих расстояние от опоры до сечения с максимальным изгибающим моментом и не более 2h₀.

Усилие Q_sw определяют по формуле

Q_sw =_swq_swc₀, (11.5)

где _sw = 0,75; q_sw – усилие в хомутах на единицу длины элемента, равное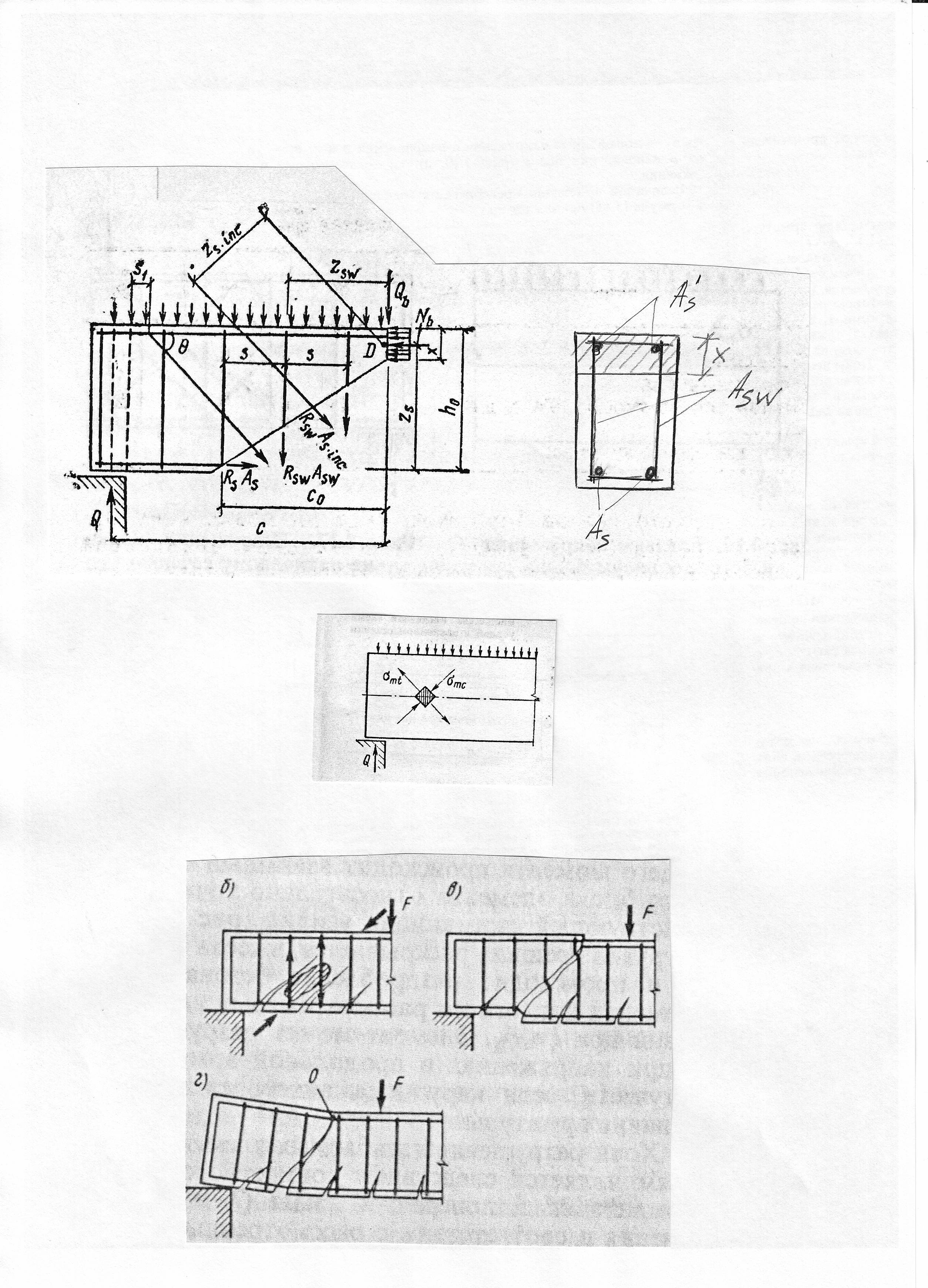


Рис.11.1. Схема усилий в наклонном сечении элементов с хомутами при расчете его на действие поперечной силы
(11.6)

Хомуты учитывают в расчете, если соблюдается условие

q_sw 0,25R_btb. (11.7)

При действии на элемент сосредоточенных сил значения c принимают равными расстояниям от опоры до точек приложения этих сил (рис.11.1), а также равными но не меньше h₀, если это значение меньше расстояния от опоры до 1-го груза.
Шаг поперечной арматуры, учитываемый в расчете должен быть не больше значения

Кроме того, хомуты должны отвечать конструктивным требованиям.
Элементы без поперечной арматуры. Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий

а) Q_max < 2,5R_btbh₀; (11.8)

гдеQ_max  максимальная поперечная сила у грани опоры;

б)_, (11.9)

где Q– поперечная сила в конце наклонного сечения, начинающегося от опоры; значение c принимается не более c_max = 3h₀.
Расчет железобетонных элементов по наклонным сечениям на действие изгибающих моментов. Расчет железобетонных элементов по наклонным сечениям на действие момента (рис.11.2) производят из условия

MM_s + M_sw, (11.10)

где M – момент в наклонном сечении с длиной проекцииcна продольную ось элемента, определяемый от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения (точка 0), противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении (Рис.11.2)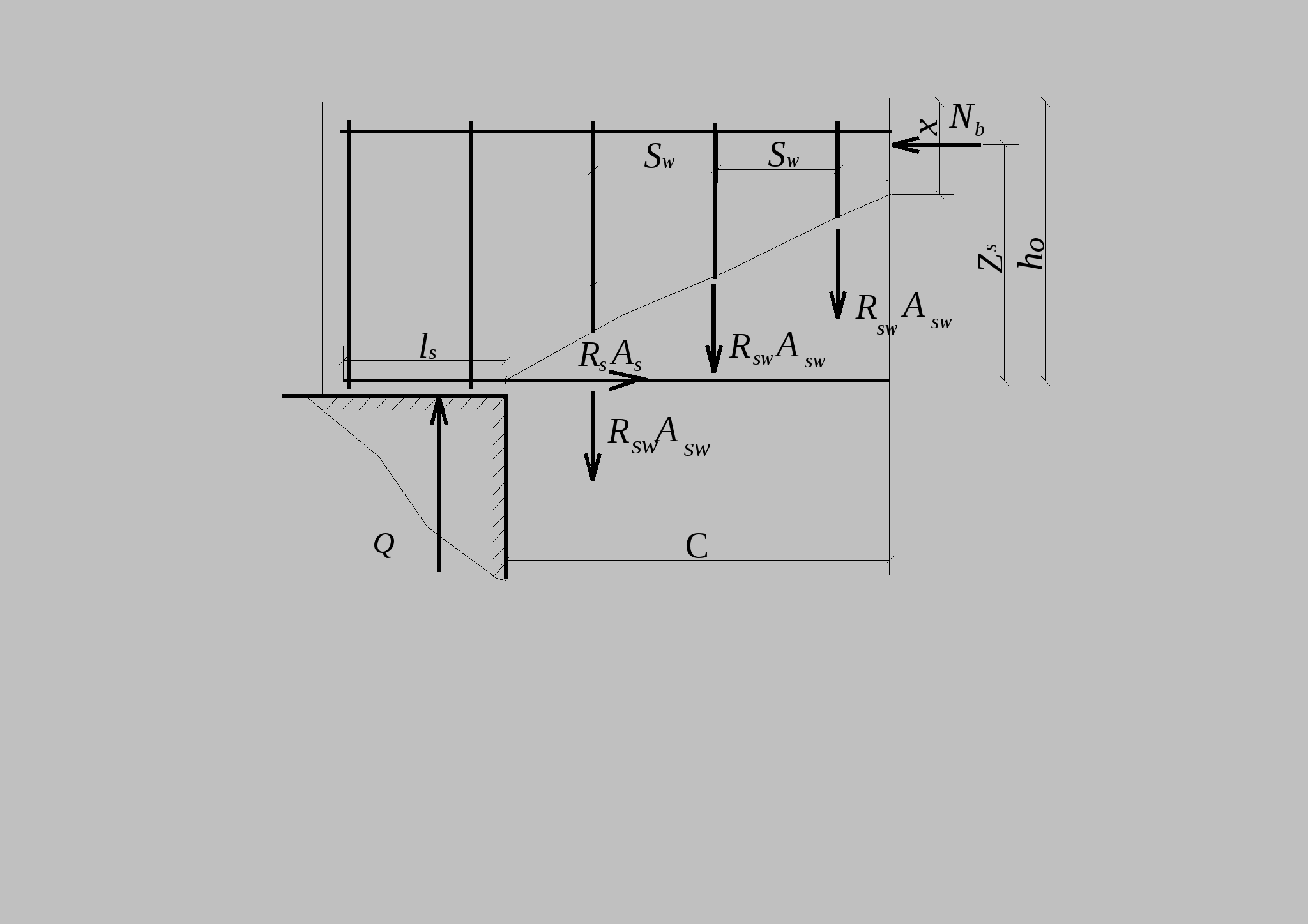


Рис.11.2. Схема усилий в наклонном сечении при расчете его по изгибающему моменту
M_s момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения;

M_sw – момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0).

Момент M_sопределяют по формуле

M_s = N_sz_s, (11.11)

где N_s усилие в продольной растянутой арматуре, принимаемое равным R_sA_s, а в зоне анкеровки определяемое в зависимости от положения относительно границы зоны анкеровки;

z_s – плечо внутренней пары сил, определяемое по формуле.

(

Момент M_swпри поперечной арматуре в виде хомутов, нормальных к продольной оси элемента, определяют по формуле

M_sw= 0,5q_sw с², (11.12)

где q_sw определяют по формуле (11.6), а с принимают не более 2h₀.

Расчет на действие момента производят для наклонных сечений, расположенных в местах обрыва продольной арматуры, а также у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров.

Кроме того, рассчитываются наклонные сечения в местах резкого изменения высоты элемента (например, в подрезках).

Поперечную арматуру следует устанавливать исходя из расчета на восприятие действующих усилий Q и M, а также с целью ограничения развития трещин, удержания продольных стержней в проектном положении и закрепления их от бокового выпучивания в любом направлении.
12. Конструктивные особенности и прочность сжатых и растянутых элементов

Конструктивные особенности. К центрально сжатым элементам условно относят средние колонны, верхние пояса ферм при узловой нагрузке, стойки ферм и т.д. В действительности из-за ряда причин центрального сжатия не существует – неоднородность бетона, несовершенство форм, отклонения от размеров. Вместо центрального сжатия вводится понятие сжатие со случайным эксцентриситетом, величина которого задается конструктивно. Сечения выполняются, как правило, квадратными или прямоугольными.

Чтобы обеспечить требуемое качество бетона сечение сжатых элементов рекомендуется проектировать размером сечения не менее 25см.

Внецентренно сжатые элементы – колонны одноэтажных промышленных зданий, крайние колонны многоэтажных рам, сжатые элементы безраскосных ферм. В сечениях элементов действуют продольные силы, изгибающие моменты и поперечные силы.

В общем случае эксцентриситет продольной силы - расстояние между линией действия силы и продольной осью элемента, определится



e_a – случайный эксцентриситет.

Для статически неопределимых конструкций случайный эксцентриситет можно не учитывать но, результат должен быть не менее случайного.

Случайный эксцентриситет принимается наибольшим из следующих значений:

- 1/30 высоты сечения элемента;

- 1/600 – длины или расстояния между закреплениями элемента;

- 10мм.

Конструктивные рекомендации:

- сечения принимают развитыми в плоскости действия момента;

- бетон класса не ниже В15;

- арматура продольная преимущественно класса А400, поперечная – А 240 –А400.

- продольную и поперечную арматуру объединяют в пространственные каркасы. Армирование продольное принимают: оптимальное – 0,5-1.2%,

максимальное, как правило, не более 3%;

- диаметры 12—40мм;

- расстояние между продольными стержнями должно быть не более 400мм;

- расстояние между поперечными стержнями должно быть: для сварных - 20d, вязанных – 15d, и не более 500мм. Поперечные стержни располагают конструктивно, как правило, без расчета;

- гибкость колонн .
Расчет прочности внецентренно сжатых элементов. Расчет ведется по 3 стадии НДС.

Усилия, воспринимаемые нормальным сечением определяются по расчетным сопротивлениям материалов с учетом коэффициентов условия работы исходя из следующих предпосылок:

-сопротивления бетона растяжению принимаются равными 0;

-сопротивление бетона сжатию равно R_b и равномерно распределено по сечению;

-деформации (напряжения) в арматуре определяются в зависимости от высоты сжатой зоны бетона;

-напряжения в растянутой арматуре принимаются не более R_S;

-напряжения в сжатой арматуре принимаются не более R_SC.

Рассматриваются два случая внецентренного сжатия:

- случай больших эксцентриситетов;

- случай малых эксцентриситетов.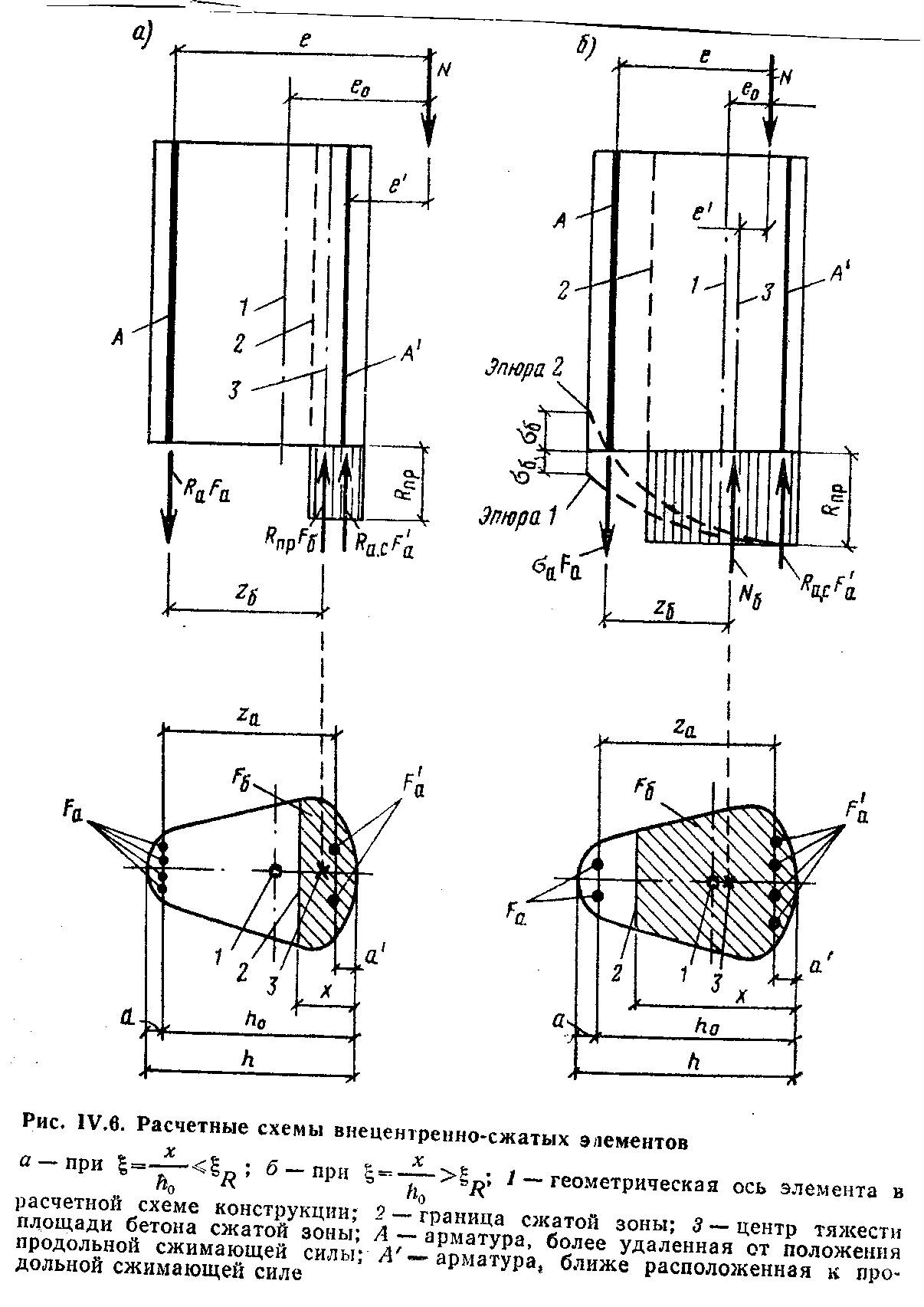



Рис.12.1.Расчетная схема работы внецентренно-сжатого нормального сечения в предельной стадии: а – случай больших эксцентриситетов; б – случай малых эксцентриситетов
Первый случай близок к характеру работы изгибаемого элемента – часть сечения растянута, в ней образуются трещины, усилие в растянутой зоне воспринимается арматурой. Предельное состояние характеризуется достижением в бетоне сжимающих напряжений равных призменной прочности бетона, а в растянутой зоне физического предела текучести. На практике начинает разрушаться сжатая зона.

Второй случай малых эксцентриситетов – здесь так же два случая: когда сечение все сжато, либо сжата его большая часть и часть сечения воспринимает слабое растяжение. Разрушение происходит по сжатой зоне. В растянутой зоне или менее сжатой арматура недоиспользуется.

Проверку прочности прямоугольных сечений производят из условия

Ne  R_bbx(h₀ – 0,5x) + R_scA (h₀ – ), (12.1)

где e – расстояние от линии действия продольной силы до растянутой или наименее сжатой арматуры, определяемое для симметричных сечений по формуле

(12.2)

где  - коэффициент, учитывающий деформированное состояние.

Высота сжатой зоны определяется из условия равновесия по формуле

(12.3)

при этом, если , это признак случая малых эксцентриситетов и высоту сжатой зоны определяют из условия равновесия
(12.4)

В приведенном выражении два неизвестных х и _x. Для решения задачи необходимо выразить напряжения в арматуре через высоту сжатой зоны. Опуская выражения для напряжений окончательно получим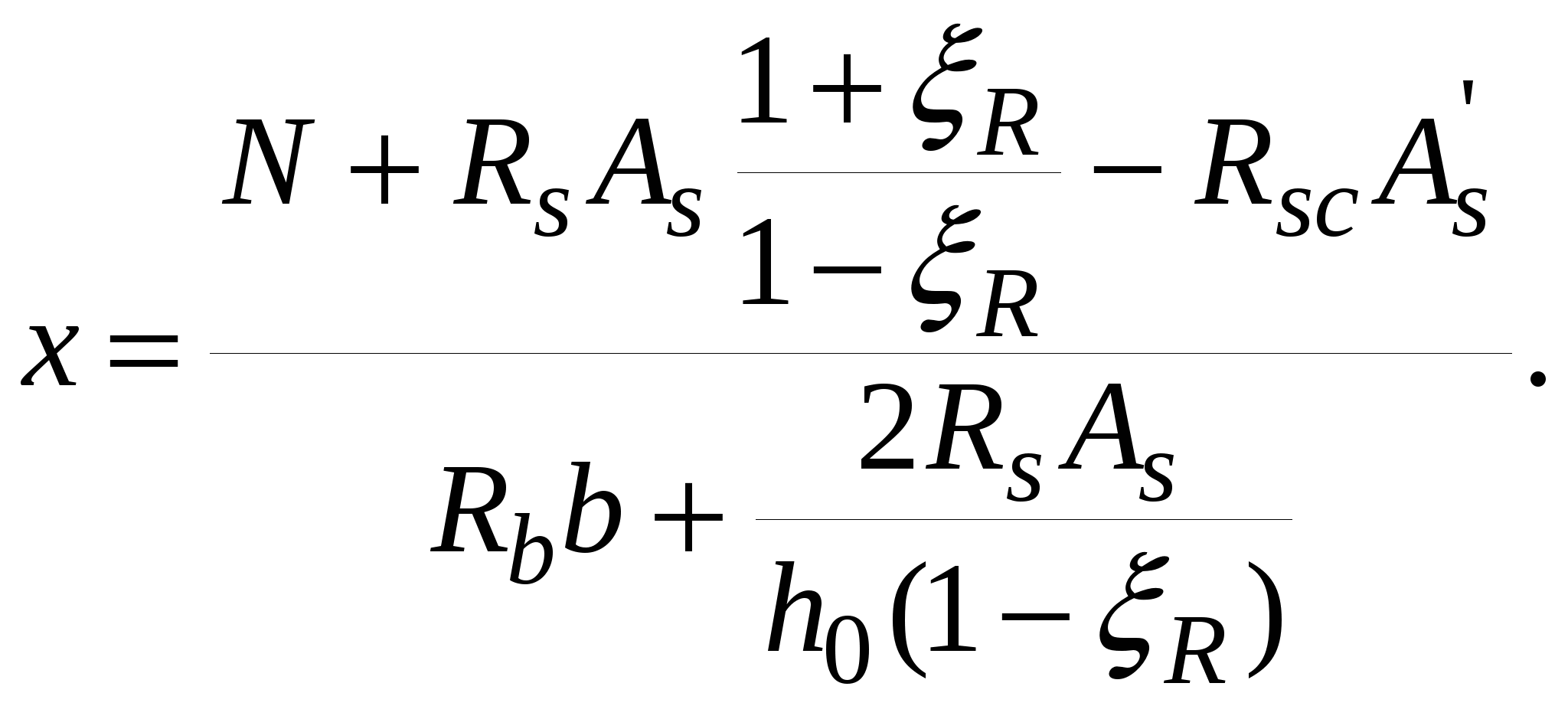

(12.5)

Учет продольного изгиба. Гибкий сжатый элемент под действием продольной силы прогибается, вследствие чего увеличивается начальный эксцентриситет, а следовательно и растет внешний изгибающий момент.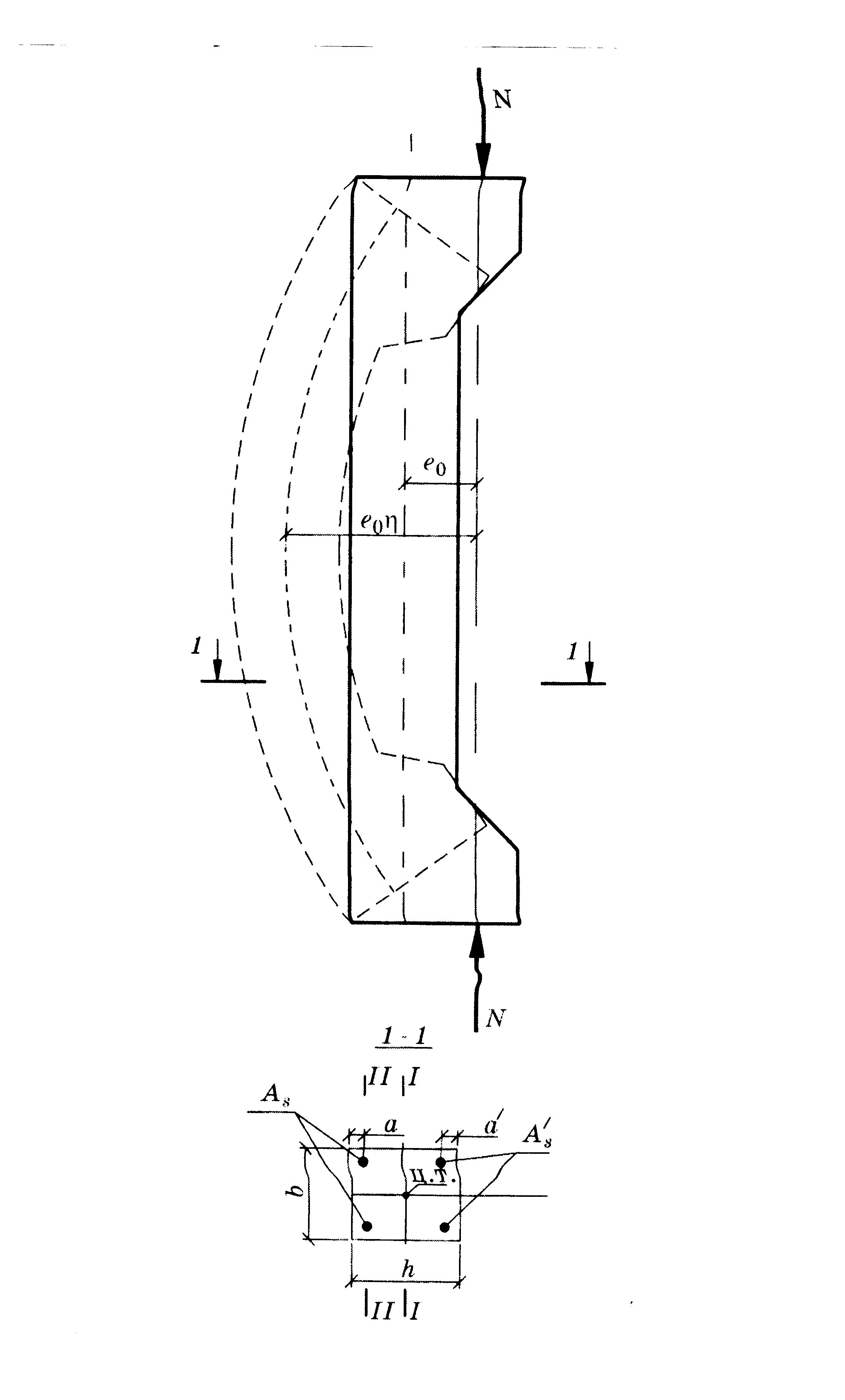


Рис.12.2. Схема деформирования внецентренно сжатого элемента
Значение коэффициента определяется по формуле

(12.6)

где N_cr – условная критическая сила, определяемая по формуле

; (12.7)

l₀ – расчетная длина элемента, определяемая для коэффициентов _vи _h ;

D – изгибная жесткость железобетонного элемента в предельной стадии.

При N > N_crследует увеличивать размеры сечения.

Расчет сжатых элементов со случайным эксцентриситетом. Расчет сжатых элементов из бетона классов В15-В35 на действие продольной силы, приложенной с эксцентриситетом, принятым равным случайному эксцентриситету
е₀ = h/30, при l₀ 20h допускается производить из условия

N(R_bA + R_scA_s,tоt), (12.8)

где - коэффициент, учитывающий длительность действия нагрузки и принимаемый в зависимости от соотношения l₀/h. При кратковременном действии нагрузки он изменяется в пределах от 0.85 до 0.9.

Расчет растянутых элементов. Расчет по прочности центрально растянутых элементов производится из условия

NR_sA_s, (12.9)

где A_s- площадь сечения всей продольной арматуры.
Внецентренно-растянутые элементы. Проверку прочности прямоугольных сечений внецентренно растянутых элементов следует производить в зависимости от положения продольной силы N:

а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S 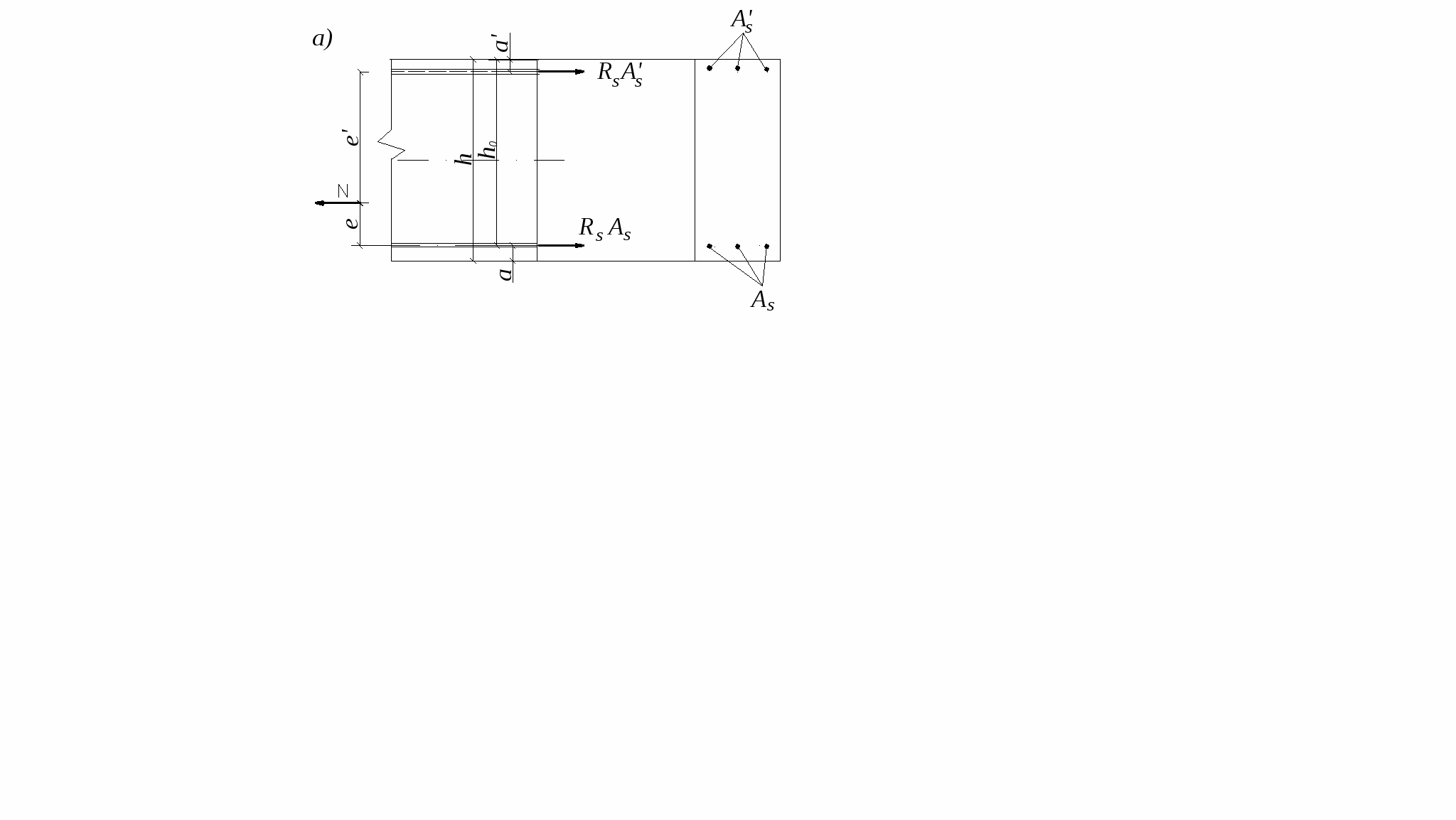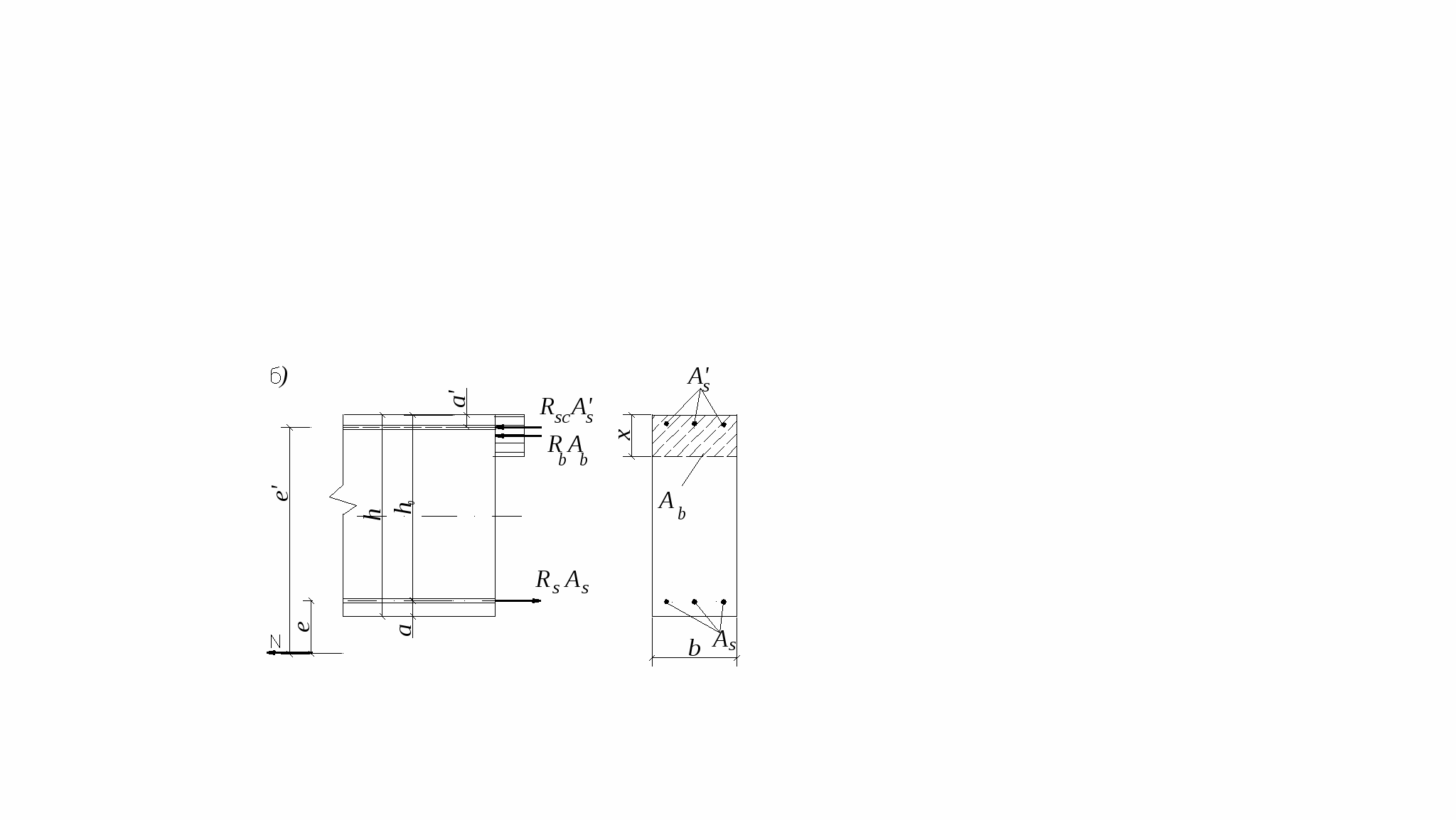(Рис.12.3,а), т.е. при eh₀ – a,  из условий

N e R_s A_s(h₀ – a); (12.10)

N e R_s A_s(h₀– a); (12.11)



Рис.12.3. Схема усилий и эпюра напряжений в сечении, нормальном к продольной

оси внецентренно-растянутого железобетонного элемента, при расчете его по

прочности

б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре SиS (рис.12.3,б), т.е. при eh₀ – a  из условия

N e  R_bbx(h₀ – 0,5x) + R_scA_s(h₀ – a’) (12.12)

при этом высота сжатой зоны x определяется по формуле

.(12.13)

Если полученное из расчета по формуле (12.13) значение x_Rh₀, в условие (12.12) подставляют x =_Rh₀, где _Rграничная высота сжатой зоны.

При х  0 прочность сечения проверяют из условия (12.12).

При симметричном армировании прочность независимо от значения e‘ проверяют из условия (12.12).

Примечание. Если при eh₀ - aвысота сжатой зоны, определенная без учета сжатой арматуры, меньше 2а, расчетную несущую способность можно несколько увеличить, произведя расчет по формулам (12.12) и (12.13) без учета сжатой арматуры.
Модуль №4. Расчет железобетонных элементов по предельным состояниям второй группы
13. Трещиностойкость железобетонных элементов

Трещиностойкостью железобетонных элементов называется способность сопротивляться образованию трещин в 1-ой стадии напряженно-деформированного состояния и сопротивление раскрытию трещин во 2-ой стадии напряженно-деформированного состояния.

К трещиностойкости ЖБК предъявляются требования в зависимости от назначения конструкции и вида применяемой арматуры. Предельно допустимая ширина раскрытия трещин:

– из условия сохранности арматуры:

а_crc = 0.3мм при продолжительном действии нагрузки;

а_crc = 0,4мм при непродолжительном действии нагрузки;

- из условия ограничения проницаемости конструкции:

а_crc = 0.2мм при продолжительном действии нагрузки;

а_crc = 0,3мм при непродолжительном действии нагрузки.

Непродолжительное раскрытие трещин а_crc1 – при действии постоянных, длительных и кратковременных нагрузок.

Продолжительное раскрытие а_crc2 – при действии постоянных и длительных нагрузок.

Предельная ширина раскрытия трещин – а_crc1 и а_crc2 непродолжительная и продолжительная ширина при которой обеспечивается нормальные условия эксплуатации, коррозионная стойкость арматуры и долговечность конструкции – изменяется в пределах 0.05 – 0.4мм.

Расчет по образованию трещин. Определение момента образования трещин, нормальных к продольной оси элемента производится из условия, что усилия, напряжения или деформации в конструкции от различных воздействий не должны превышать соответствующих им предельных значений при образовании трещин.

При учете неупругих деформаций растянутого бетона приняты предпосылки:

- стадия НДС -1;

- справедлива гипотеза плоских сечений;

-наибольшие удлинения крайнего растянутого волокна соответствуют предельным

; (13.1)

- напряжения в сжатой зоне распределяются по треугольному закону;

- напряжения в растянутой зоне бетона соответствуют предельным на растяжение.

Момент образования трещин без учета неупругих деформаций растянутого бетона определяют по формуле

, (13.2)

где W– момент сопротивления приведенного сечения для крайнего растянутого волокна бетона:

e_Х– расстояние от центра тяжести приведенного сечения элемента до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.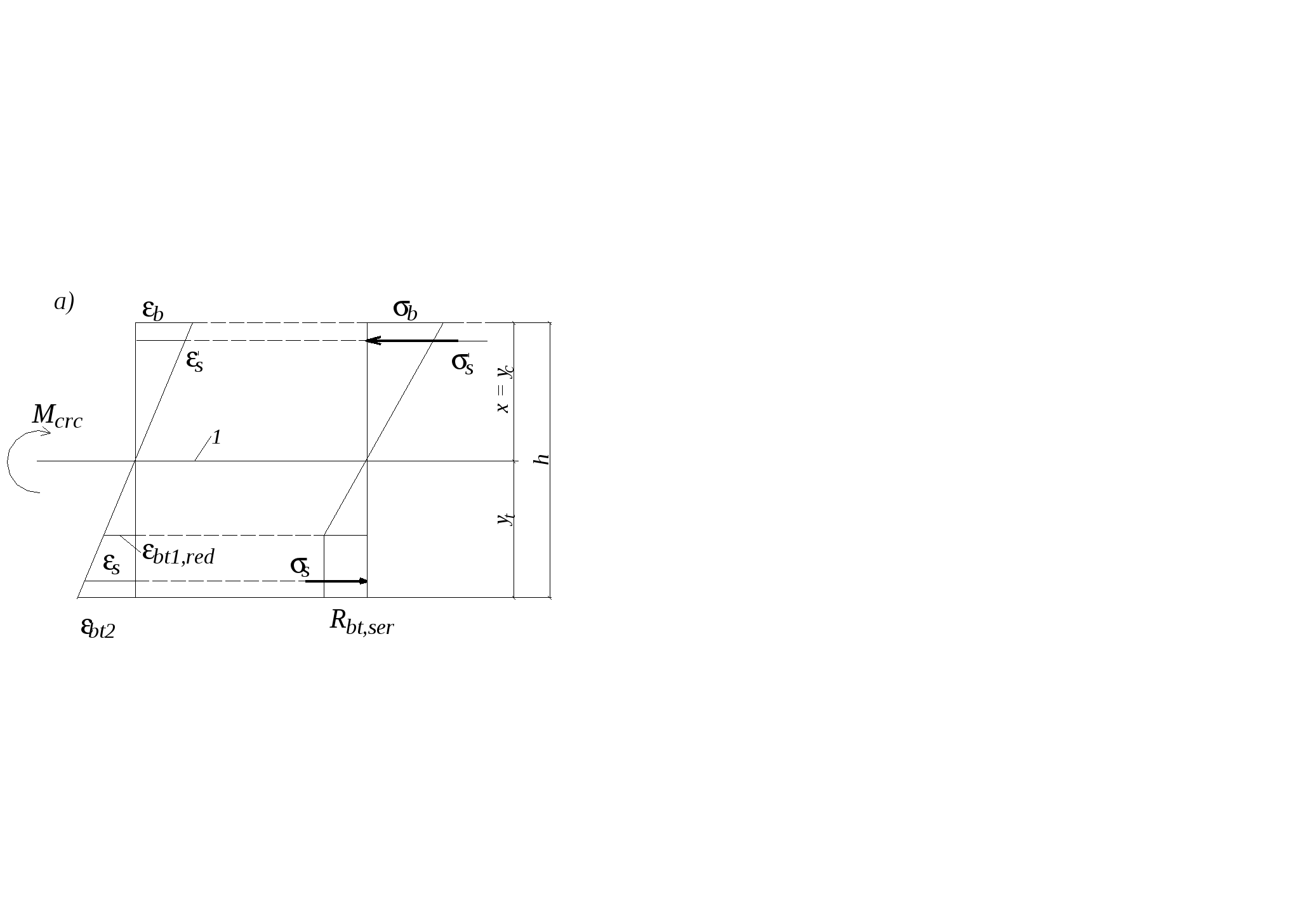


Рис.13.1. Схема напряженно-деформированного состояния сечения элемента при

проверке образования трещин при действии изгибающего момента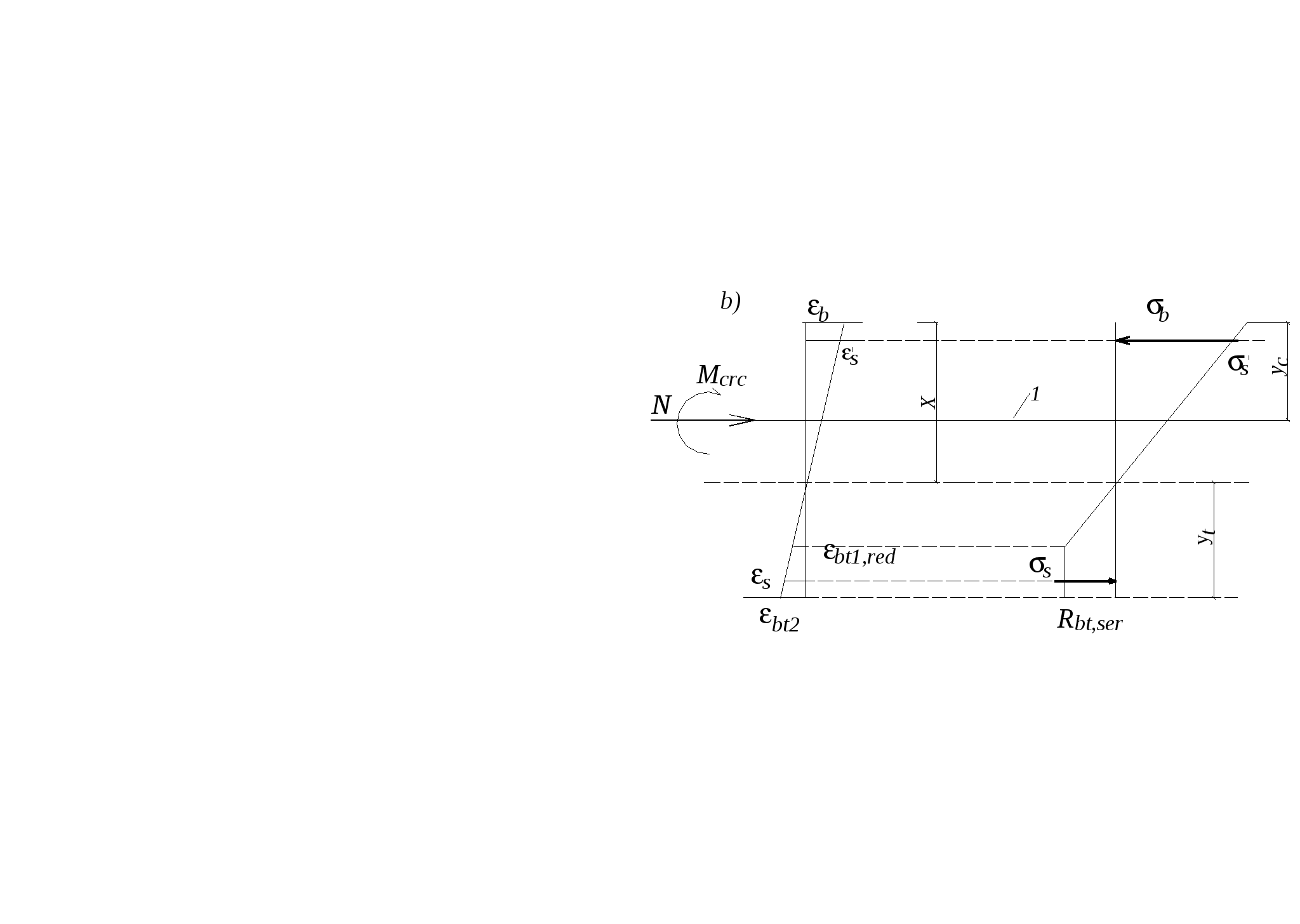



Рис.13.2.Схема напряженно-деформированного состояния сечения элемента при проверке образования трещин при действии изгибающего момента и продольной силы (б)

В формуле (13.2) знак “плюс” принимают при сжимающей продольной силе N , знак “минус” – при растягивающей силе.

Момент сопротивления W и расстояние e_я определяют по формулам:

W = , (13.3)

(13.4)

где I_red– момент инерции приведенного сечения относительно его центра тяжести, определяемый по формуле

I_red=I+I_s+I_s ; (13.5)

I, I_s, – моменты инерции сечения соответственно бетона, растянутой и сжатой арматуры;

A_red– площадь приведенного сечения, равная

A_red = A + A_s+ , (13.6)

= – коэффициент приведения арматуры к бетону;

y_t– расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного сечения элемента
.

Момент образования трещин предварительно напряженных изгибаемых элементов без учета неупругих деформаций растянутого бетона (рис.13.3) определяют по формуле

, (13.7)

где е_0р – эксцентриситет усилия обжатия Р относительно центра тяжести приведенного сечения;

r – расстояние от центра тяжести приведенного сечения до ядровой точки, значение r определяется по формуле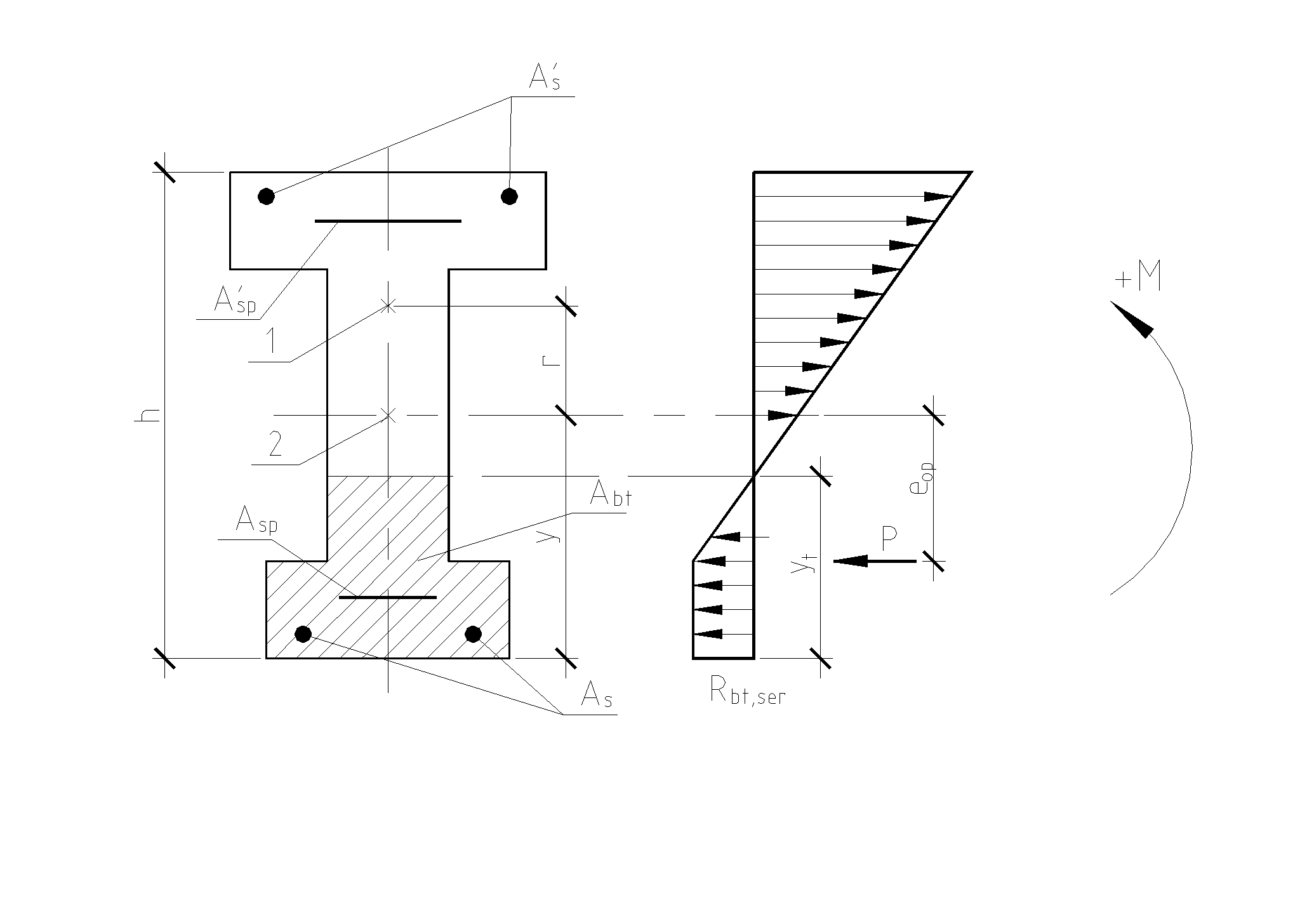

,(13.8)



Рис.13.3. Схема усилий и эпюра напряжений в поперечном сечении элемента при расчете по образованию трещин в стадии эксплуатации

1 - ядровая точка; 2 - центр тяжести приведенного сечения
Определение ширины раскрытия трещин, нормальных к продольной оси элемента. Расчет по раскрытию трещин не производится, если соблюдается условие

M < M_crc, (13.9)

где М – изгибающий момент от внешней нагрузки;

M_crc – изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин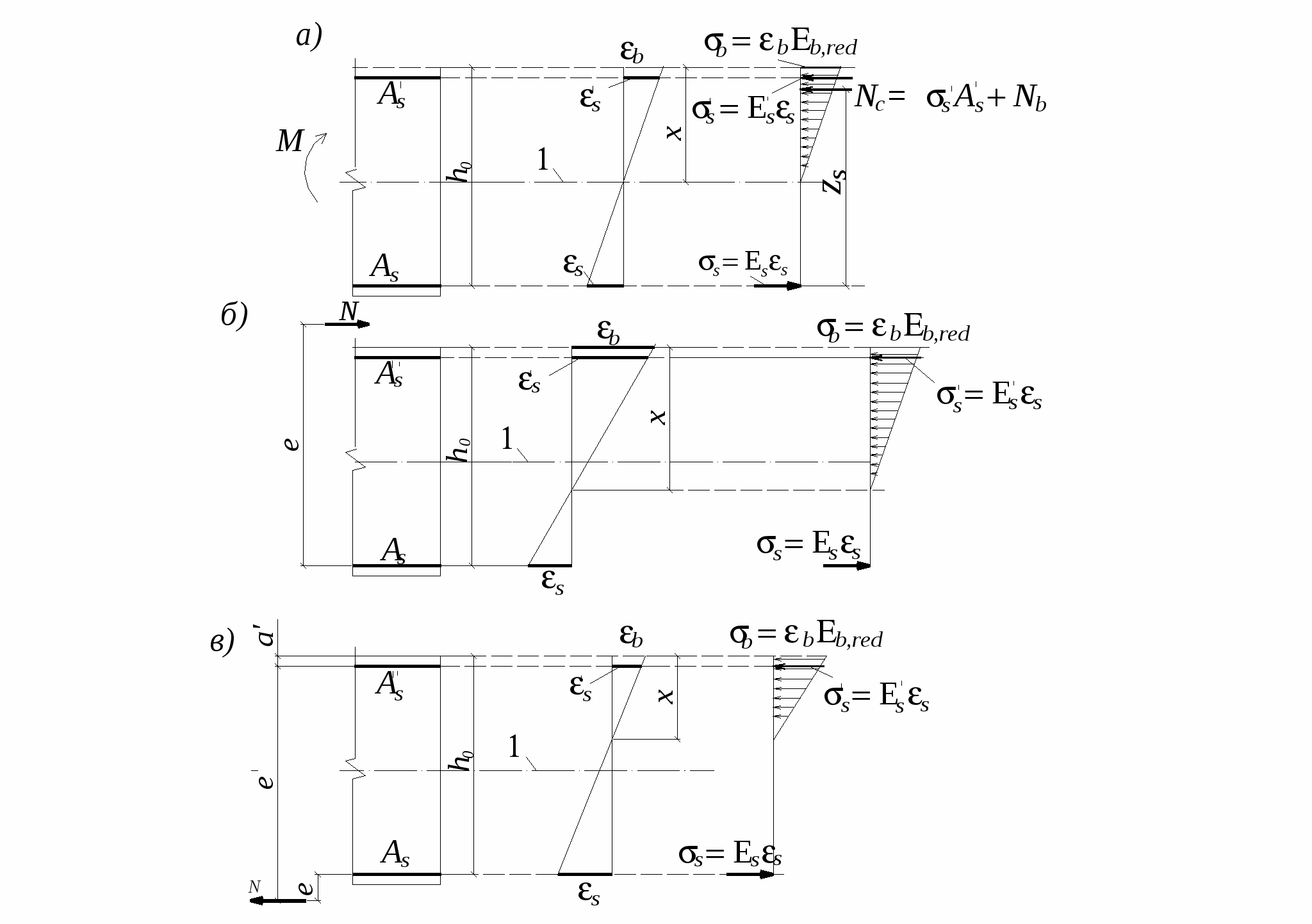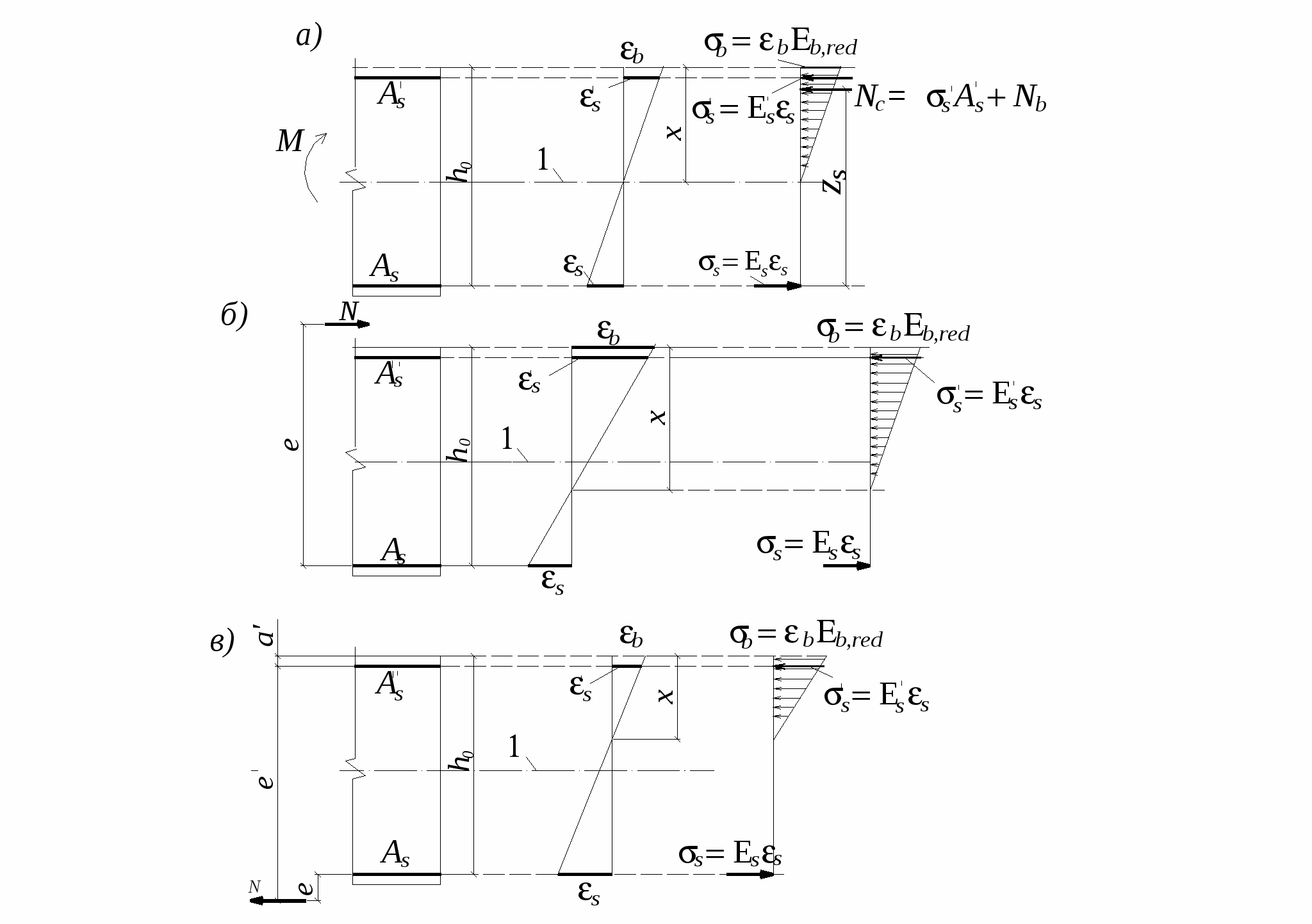





Рис.13.4. Расчетная схема напряженно-деформированного состояния нормального сечения элемента с трещинами при действии: изгибающего момента (а), сжимающей продольной силы (б): 1 – уровень центра тяжести приведенного сечения

Ширину раскрытия нормальных трещин определяют по формуле

a_crc = ₁₂₃_s, (13.10)

где σ_s –напряжения в продольной арматуре в сечении с трещиной от внешней нагрузки;

l_s – базовое (без учета вида внешней поверхности арматуры) расстояние между смежными нормальными трещинами;

φ₁ – коэффициент, учитывающий продолжительность действия нагрузки и принимаемый равным:

1,0 – при непродолжительном действии нагрузки;

1,4 – при продолжительном действии нагрузки;

φ₂ – коэффициент, учитывающий профиль арматуры и принимаемый равным:

0,5 – для арматуры периодического профиля и канатной;

0,8 – для гладкой арматуры (класса А240);

φ₃ - коэффициент, учитывающий характер нагружения, для изгибаемых и внецентренно сжатых элементов равен 1;

ψ_s – коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать ψ_s = 1.

Напряжения σ_s в растянутой арматуре изгибаемых предварительно напряженных элементов определяют по формуле

, (13.11)

где J_red,A_red,y_C–момент инерции, площадь приведенного сечения и расстояние от наиболее сжатого волокна до ц.т. сечения, определяемые только с учетом площади сжатой зоны бетона и арматуры;

M_P – момент от внешней нагрузки и усилия предварительного обжатия, равный

.

Значение коэффициента приведения арматуры к бетону определяют по формуле , (13.12)

где E_b,red – приведенный модуль деформации сжатого бетона, равный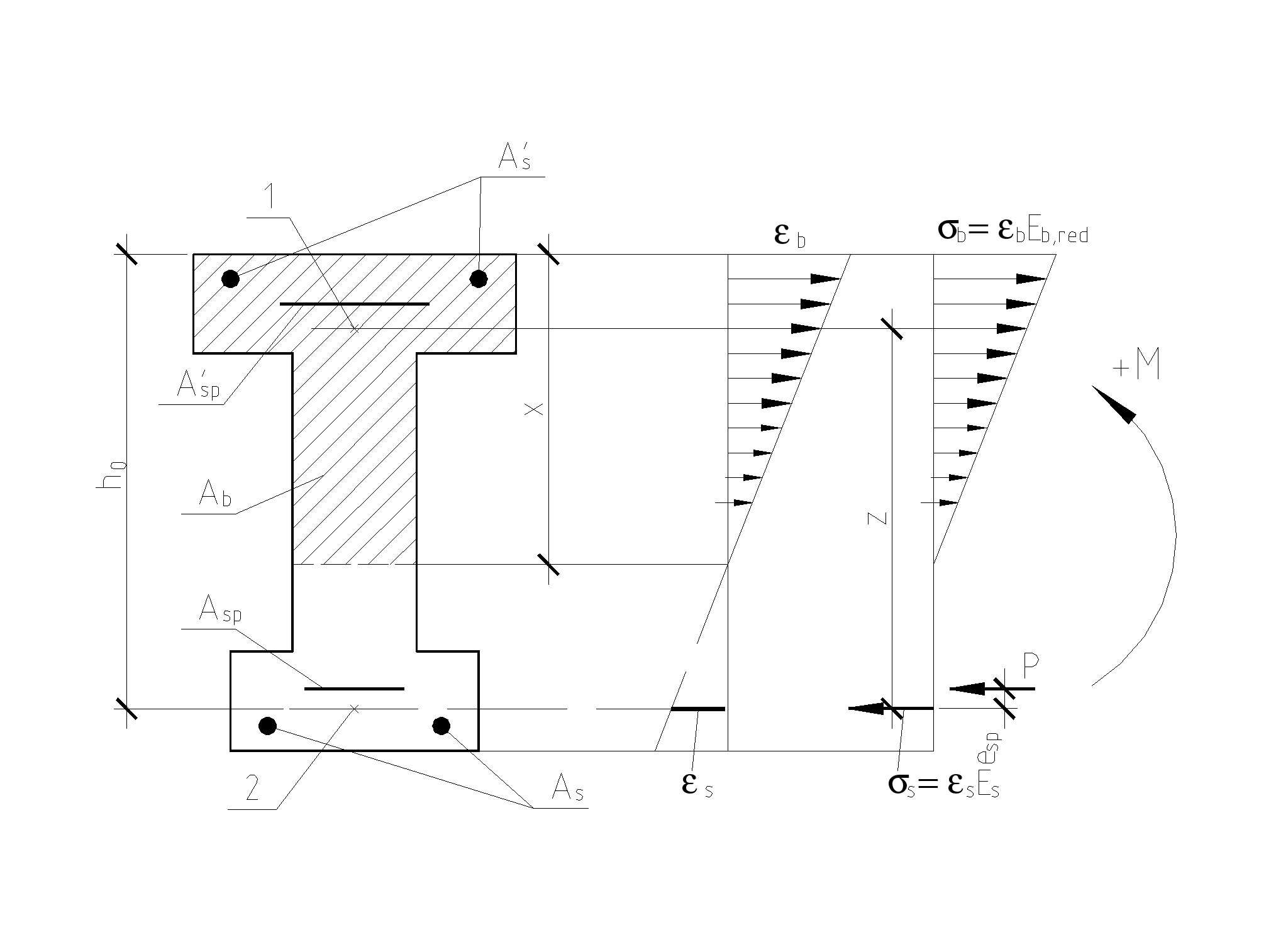

, .



Рис.13.5. Схемы усилий и напряженно-деформированного состояния сечения с трещиной в стадии эксплуатации при расчете по раскрытию трещин:

1 – точка приложения равнодействующей усилий в сжатой зоне; 2 – центр тяжести сечения арматуры S
Ширину раскрытия трещин принимают равной:

при продолжительном раскрытии

a_crc = a_crc1; (13.13)

при непродолжительном раскрытии

a_crc = a_crc1 + a_crc2 – a_crc3, (13.14)

где a_crc1 – ширина раскрытия трещин при действии постоянных и длительных нагрузок (т.е. при M = M_l);

a_crc2 – ширина раскрытия трещин от непродолжительного действия всех нагрузок (т.е.при
M = M_tot);

a_crc3 – непродолжительное действие постоянных и длительных нагрузок (т.е. при M = M_l).