задачи4модуль. Модуль 4 Случайные величины
 Скачать 173.5 Kb. Скачать 173.5 Kb.
|
|
МОДУЛЬ 4 Случайные величины 1. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить распределение вероятностей дискретной случайной величины Х – числа стандартных деталей среди отобранных и найти ее математическое ожидание. 2. ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится 5 изделий. Найти математическое ожидание дискретной случайной величины Х-числа партий, в каждой из которых окажется ровно 4 стандартных изделия – если проверке подлежит 50 партий. 3. Среди пяти ключей два подходят к двери. Ключи пробуют один за другим, пока не откроют дверь. Найти распределение вероятностей для числа опробованных дверей. 4. Закон распределения случайной величины Х имеет вид
Найти функцию распределения случайной величины Х, вычислить ее математическое ожидание, дисперсию и среднеквадратическое отклонение. Вычислить вероятность 5. Распределение случайной величины
Найти функцию распределения, построить её график. Найти математическое ожидание и дисперсию случайной величины 6. Дискретная случайная величина имеет закон распределения:
Найти 7. Плотность распределения случайной величины Х имеет вид 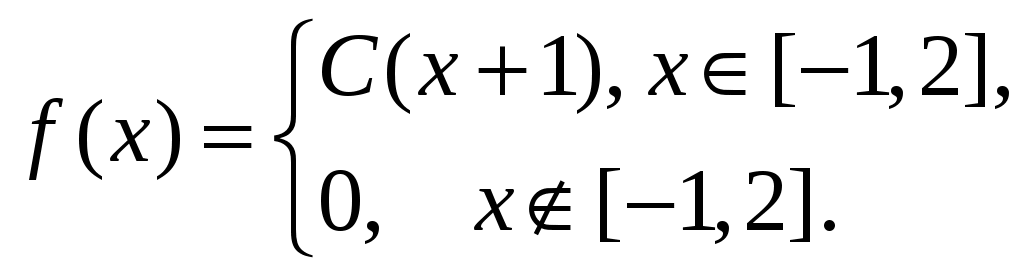 Вычислить константу 8. Проверить, что функция 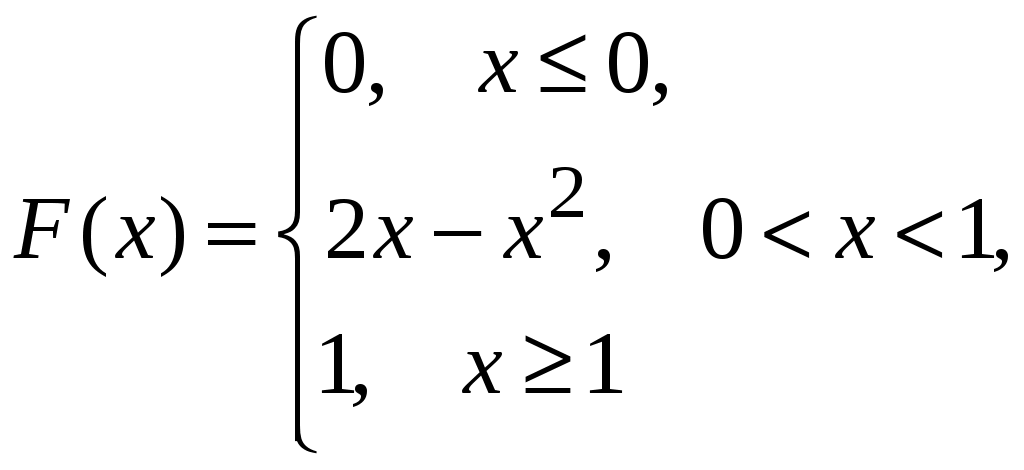 может быть функцией распределения некоторой случайной величины. Найти числовые характеристики этой случайной величины. 9. Случайная величина 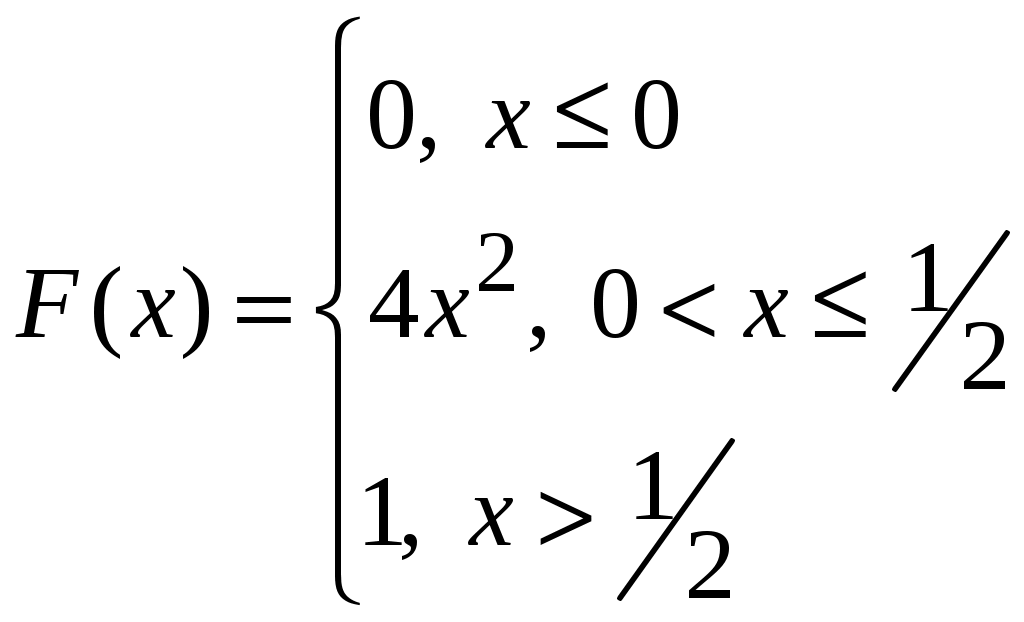 Найти плотность распределения, математическое ожидание и дисперсию случайной величины. 10. Случайная величина 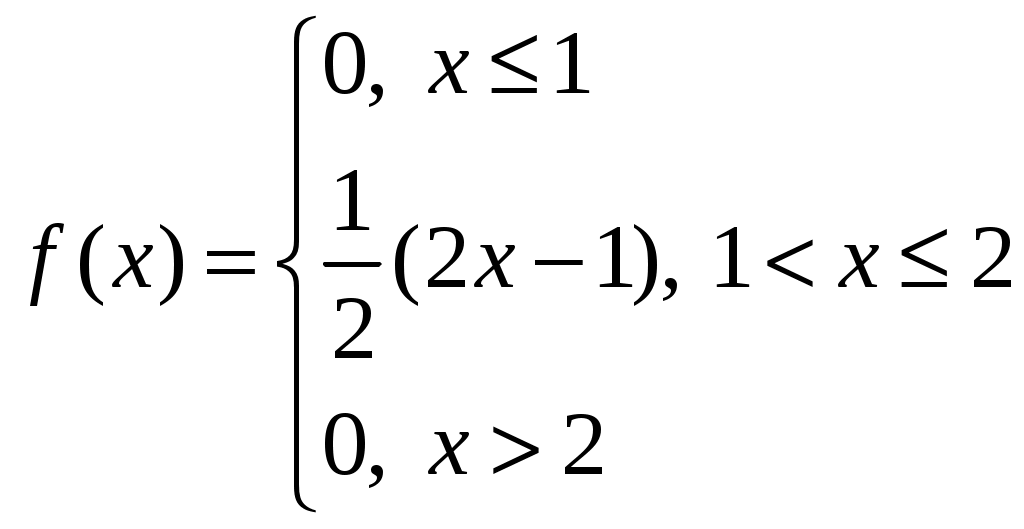 Найти функцию распределения, математическое ожидание и дисперсию случайной величины 11. Случайная величина 12. В партии из 10 деталей – 8 стандартных. Наудачу отобраны 2 детали. Составить закон распределения числа стандартных деталей среди отобранных. 13. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно 3 изделия; б) менее трех. 14. Найти дисперсию и среднее квадратическое отклонение показательного закона, заданного функцией распределения 15. Найти дисперсию и среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности Ответы. 1) 3)
4) 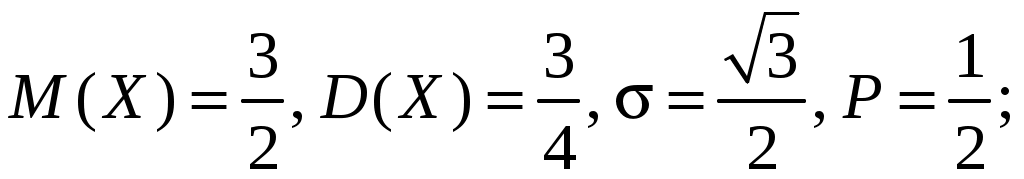 5) 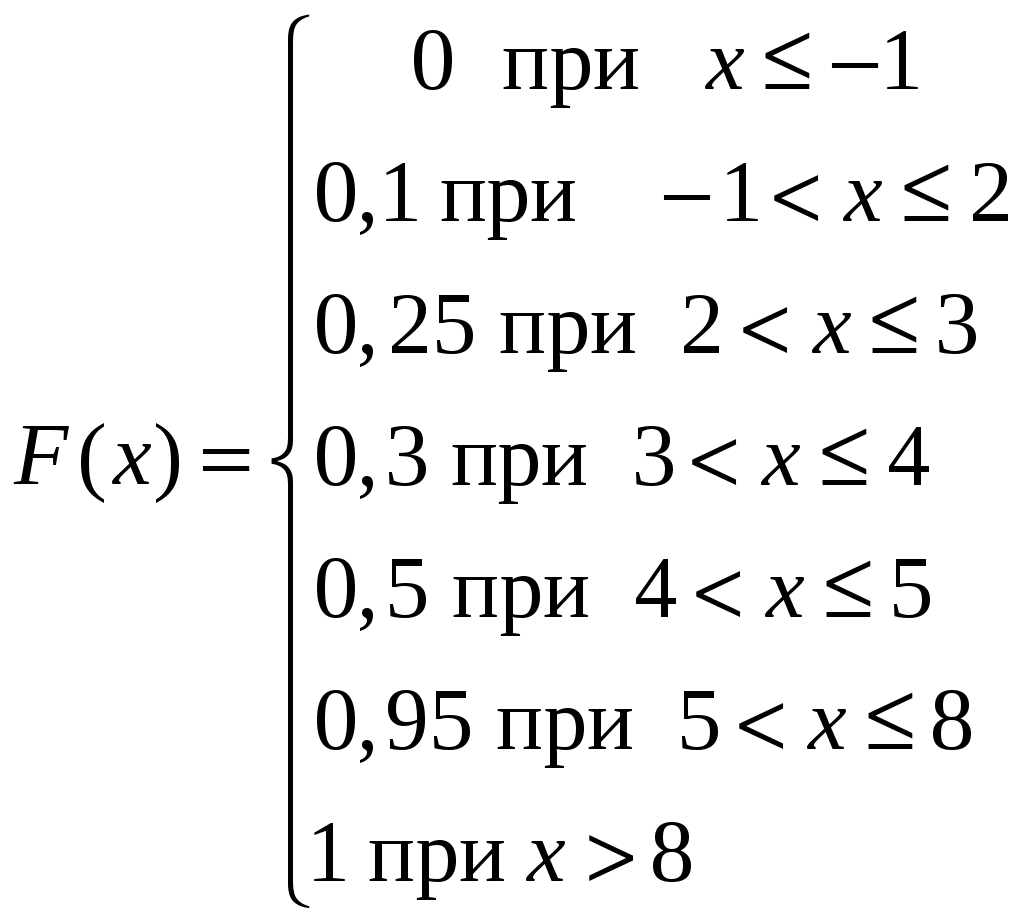 ; ; 6) 8) 9) 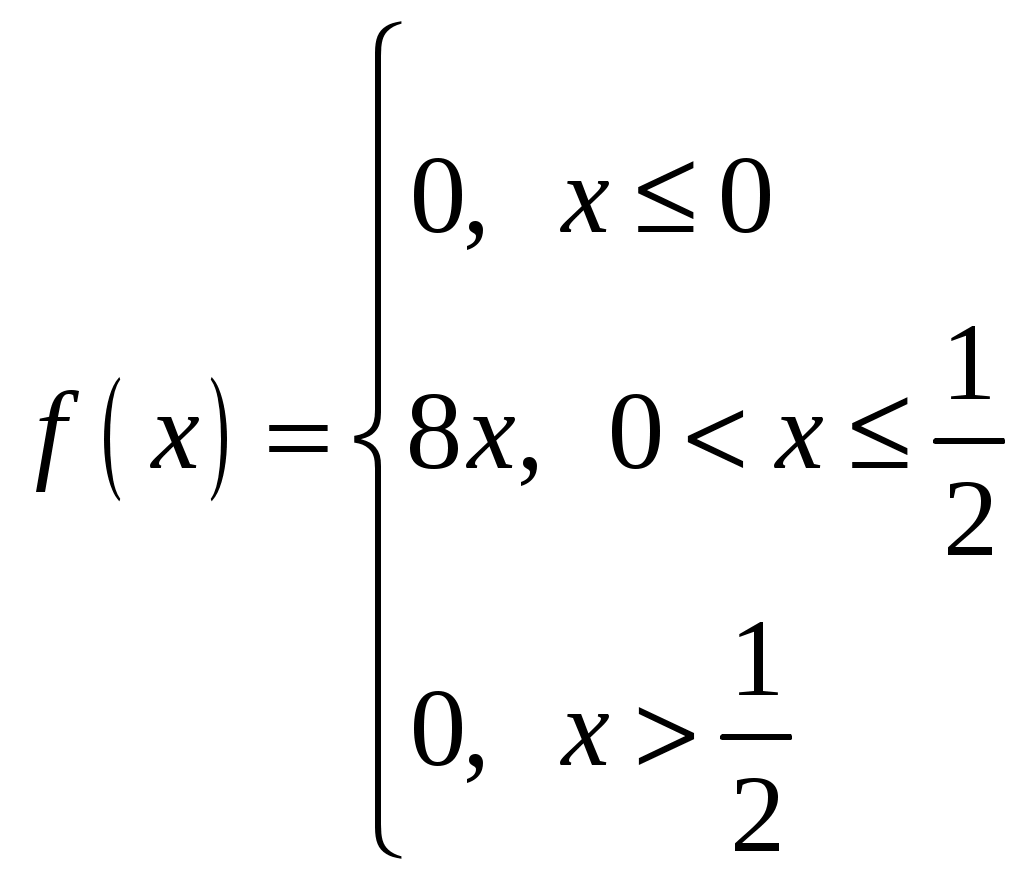 ; ; 10) 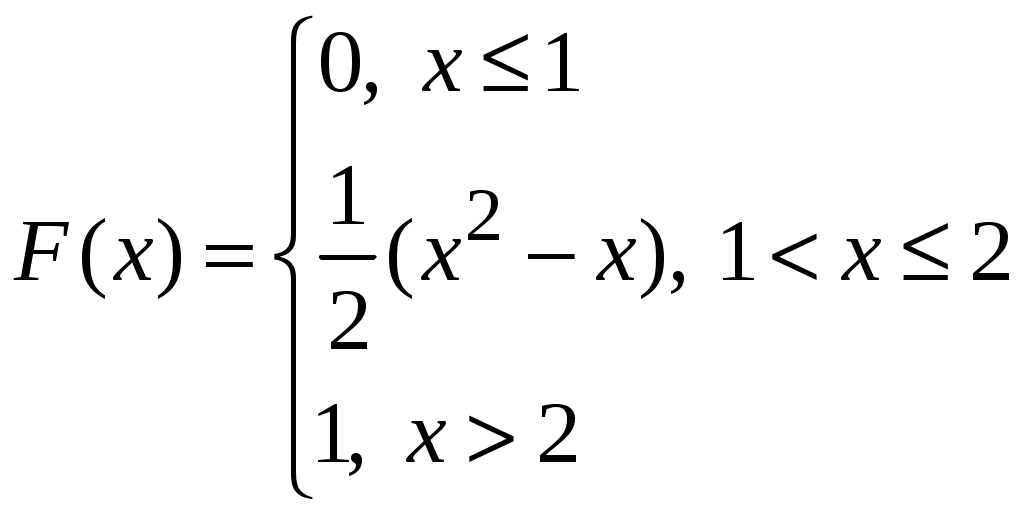 ; ; 11) 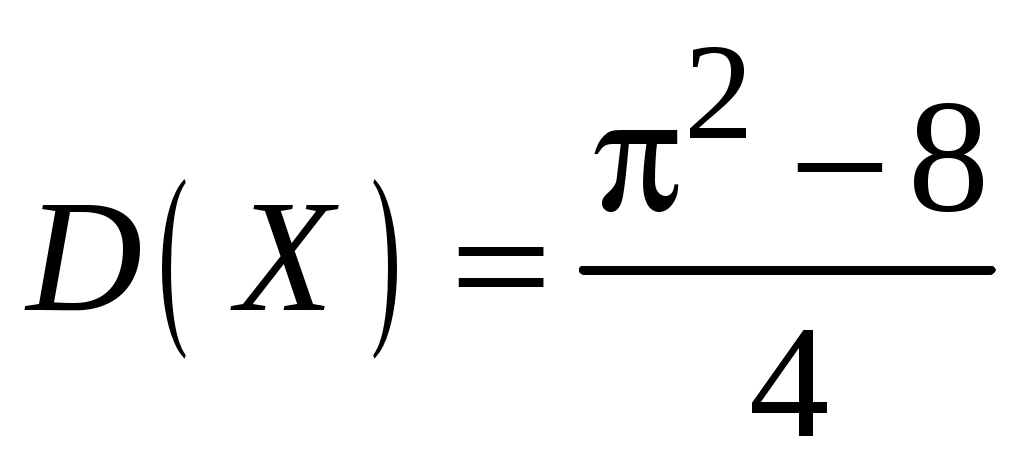 ; ; 12)
13) а) 0,0613; б) 0,9197; 14) |
