Расчет зубчатого зацепления. Зубчатое зацепление. Модуль зубьев

• Название: Модуль зубьев
• Анкор: Расчет зубчатого зацепления
• Дата: 01.05.2023
• Размер: 28.02 Kb.
• Имя файла: Зубчатое зацепление.docx
• Тип: Документы; #1100176

Задание 1

Выполнить синтез зацепления равносмещённой эвольвентной цилиндрической зубчатой передачи внешнего зацепления при следующих исходных данных:

модуль зубьев m = 20 мм;

числа зубьев зацепляющихся колёс z₁ = 13, z₂ = 23;

параметры исходного контура по ГОСТ 13755-81:

а) угол профиля зуба α = 20°

б) коэффициент высоты головки зуба = 1

в) коэффициент высоты ножки зуба 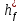= 1,25

г) коэффициент радиального зазора = 0,25

д) коэффициент радиуса кривизны переходной кривой = 0,38
Геометрический расчёт

1) Радиусы делительных окружностей:

r₁ =0,5·m·z₁ = 0,5·20·13= 130 мм

r₂ = 0,5·m·z₂ =0,5·20·23= 230 мм

2) Делительное межосевое расстояние:

a = r₁ + r₂ = 130 + 230 = 360 мм

3) Радиусы основных окружностей:

r_b1 = r₁·cos α = 130·cos 20°= 122.2 мм

r_b2 = r₂·cos α = 230·cos 20°= 216.2 мм

4) Так как проектируемая передача является равносмещённой, то

а) суммарный коэффициент смещения x_Σ= 0;

б) угол зацепления α_w = α = 20°.

Значит радиусы начальных и делительных окружностей равны между собой:

r_w1 = r₁ =130 мм

r_w2 = r₂ = 230 мм

Тогда начальное межосевое расстояние равно делительному:

a_w = a = 360 мм

5) Коэффициенты смещения зуборезного инструмента

x_1min = = = 0,24

0,18 ≤ x₁ = 0,3 значит условие (3.44) выполнено

x_2min = = 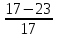≈ - 0,35

Принимаем x₁ = 0,24; x₂= - x₁ =- 0,24.

6) Абсолютные сдвиги рейки:

C₁ = x₁·m=0,24·20= 4,8мм

C₂ = x₂·m= (- 0,24)·20= - 4,8мм

7) Радиусы окружностей впадин:

r_f1 =r₁ - 1,25·m + C₁ = 130 - 1,25·20 + 4,8= 109.8 мм

r_f2 =r₂- 1,25·m + C₂ =230- 1,25·20 – 4,8 = 200,2 мм

8) Радиусы окружностей вершин:

r_a1 = r₁ + m + C₁ = 130 + 20 + 4,8 = 154,8 мм

r_a2 = r₂+ m + C₂ =230+ 20 – 4,8 = 245,2 мм

9) Высота зуба:

h = 2,25·m=2,25·20 = 45,0 мм

Проверка:

h₁= r_a1 -r_f1 = 154.8 – 109.8 = 45,0 мм

h₂ = r_a2 -r_f2 = 245.2 – 200.2 = 45,0 мм

То есть h₁= h₂ =h.

Значит радиусы окружностей вершин и впадин зацепляющихся колёс определены верно.

10) Угловые шаги зубьев:

τ₁= 360 / z₁ =360 / 13 = 27.69°

τ₂= 360 / z₂ =360 / 23 = 15.65°

11) Шаг зубьев по делительной окружности:

p = π·m= 3,14·20= 62.8 мм

12) Толщины зубьев по делительным окружностям:

S₁ =0,5·p + 2·C₁·tg α =0,5·62.8 + 2·4,8·tg 20°= 36.2 мм

S₂ =0,5·p + 2·C₂·tg α=0,5·62.8 + 2·(- 4,8)·tg 20°= 26.6 мм

13) Коэффициент перекрытия

Определяем длину практической линии зацепления аналитически:

ab = + 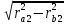- a_w·sinα_w = + - 360·sin 20° = 88.271 мм

Тогда, коэффициент перекрытия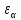

= = = 1,49

Построение картины зацепления
Исходными данными к выполнению построения являются результаты геометрического расчёта.

Построение картины зацепления можно разбить на два этапа. На первом этапе прорисовываются дуги концентрических окружностей (делительных, начальных и т.д.), прямая n-n (общая касательная к основным окружностям), определяется положение полюса зацепления, а также точек теоретической и практической линий зацепления. На втором этапе выполняется построение профилей зубьев.

Порядок выполнения первого этапа:

а) Обозначьте точку О₁–центр вращения зубчатого колеса 1.

б) Через точку О₁ проведите прямую – линию центров зацепляющихся зубчатых колёс 1 и 2.

в) На линии центров от точки О₁ отложите отрезок О₁О₂= а_w, полученная при этом точка О₂ будет являться центром вращения зубчатого колеса 2.

г) Через точку О₁ проведите прямую, составляющую угол зацепления α_w с линией центров и откладываем на ней отрезок О₁A = r_b1.

д) Через точку О₂ проведите прямую, составляющую угол зацепления α_w с линией центров и откладываем на ней отрезок О₂B = r_b2.

e) Через точки А и В проведите прямую и обозначьте её n-n.

Пересечение прямой n-n с линией центров даёт точку Р – полюс зацепления. Полученный отрезок AB является теоретической линией зацепления.

ж) Постройте дуги окружностей радиусами r_f1 (впадин); r_b1 (основная); r₁ (делительная); r_w1 (начальная); r_a1 (выступов) для зубчатого колеса 1 с центром в точке О₁.

з) Постройте дуги окружностей радиусами r_f2; r_b2; r₂; r_w2; r_a2 для зубчатого колеса 2 с центром в точке О₂.

Дуги начальных окружностейr_w1 и r_w2 должны касаться в полюсе зацепления Р.

Пересечение прямой n-n с дугой окружности r_a2даёт точку a, а c дугой окружности r_a1 – точку b. Полученный отрезок ab является практической линией зацепления.

рабочего (эвольвентного) профиля с дугой окружности впадин с помощью кривой радиусом ρ, величина которого определяется с помощью формулы (3.13). Такой способ построения переходной кривой от рабочей части зуба до его впадины является упрощённым. Фактически такая кривая получается автоматически при нарезании зубьев методом обкатки [Пузырёв, с. 72-74].

При профилировании зуба сначала строится его половина, а вторая половина симметрируется относительно оси симметрии. Построение половины зуба начинается с его рабочего (эвольвентного) профиля. Участок зуба от дуги окружности впадин до дуги основной окружности строится сопряжением кривой рабочего (эвольвентного) профиля с дугой окружности впадин с помощью кривой радиусом ρ, величина которого определяется с помощью формулы:

ρ = ·m = 0,38∙ 20= 7.60 мм