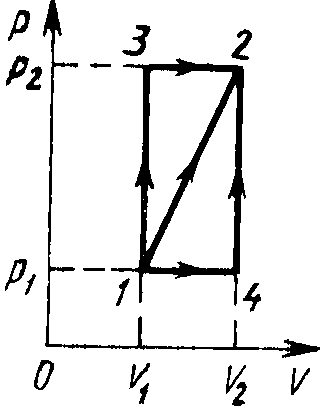Молекулярная физика и термодинамика Основные понятия молекулярной физики
 Скачать 228 Kb. Скачать 228 Kb.
|
|
Молекулярная физика и термодинамика 1. Основные понятия молекулярной физики 1.1. Найти молекулярную массу молекул О2 и Н2О в килограммах и атомных единицах. Определить молярную массу этих веществ. 1.2. Найти число молей в 100 г чистой воды и в 100 г поваренной соли NaCl. 1.3. Микроскопическая пылинка углерода обладает массой 0,1 нг. Определить, из скольких атомов, она состоит. 1.4. Приняв, что воздух по массе состоит из 78% азота, 21% кислорода и 1% аргона, найти массу 1 моль воздуха. 1.5. Сколько частиц (атомов и молекул) находится в азоте массой 1 г, если степень диссоциации азота = 7%. 1.6. Оценить размеры атома меди. Плотность меди 8600 кг/м3. 1.7. Определить число молекул в литре воды. Плотность воды 1000 кг/м3. 1.8. Где содержится больше атомов: в 1000 см3 чистого льда или в 1 кг чистого алюминия? 1.9. Сколько содержится молекул в 1 м3 чистого железа. Д1.1. Найти молекулярную массу молекул KCl, C2H2O2 в килограммах и атомных единицах. Определить молярную массу этих веществ. Д1.2. Найти число молей в 1 литре этанола С2H5OH. Плотность этанола 790 кг/м3. Д1.3. Оценить средний размер молекул воды. Плотность воды 1000 кг/м3. Д1.4. Как, зная плотность вещества и молярную массу, определить число молекул в единице объема? Определить концентрацию молекул воды. 2. Основное уравнение МКТ. 2.1. Оценить среднюю квадратичную скорость человека средней массы (70 кг) при 20ºС. Каково давление, создаваемое группой студентов на стенки аудитории? 2.2. Рассчитать среднеквадратичную скорость молекул кислорода, водорода, аргона. 2.3. В сосуде объемом 2 л находится газ под давлением 0,5 МПа при нормальной температуре. Чему равна средняя кинетическая энергия поступательного движения одной молекулы газа и всего газа в целом? 2.4. Для дальней космической связи используется спутник объемом 100 м3, наполненный воздухом при нормальных условиях. Метеорит пробивает в его корпусе отверстие площадью S = 1,0 см2. Найти время, через которое давление внутри спутника изменится на 1,0%. Температуру газа считать неизменной. 2.5. В герметичном сосуде смешали поровну кислород и гелий, а затем в стенке сосуда сделали отверстие. Каков состав молекулярного пучка, выходящего через него? Рассмотреть случаи равной массы и равного количества вещества. Д2.1. Во сколько раз средняя квадратичная скорость пылинки, взвешенной в воздухе, меньше средней квадратичной скорости молекул воздуха? Масса пылинки 10-8 г. Воздух считать однородным газом c молярной массой 0,029 кг/моль. Д2.2. Найти импульс молекулы водорода при температуре t = 20°С. Скорость молекулы считать равной средней квадратичной скорости. Д2.3. Определить среднюю кинетическую энергию поступательного движения одной молекулы водорода и 1 моля при 20ºС. 3. Газовые законы. Уравнение состояния идеального газа.
3.2. Газ находится при температуре 20°С и давлении 0,50 МПа. Какое давление потребуется для того, чтобы увеличить плотность газа в 2 раза, если температура его будет доведена до 80°С? 3.3. Давление в цилиндре паровой машины объёмом 20 дм3 после открывания клапана уменьшилось на 0,81 МПа. Какова масса пара при температуре 100о С, выпущенного из цилиндра? 3.4. В сосуде объемом 3,0 дм3 находится гелий массой 4,0 мг, азот массой 70 мг и 5,01021 молекул водорода. Каково давление смеси, если ее температура 27°С? 3.5. Сколько качаний n поршневого насоса надо сделать, чтобы накачать пустую камеру футбольного мяча объемом V = 2,5 дм3 до давления, превышающего атмосферное в 4 раза? За каждое качание насос захватывает из атмосферы воздух объемом V0 = 200 см3. Температуру мяча считать постоянной. 3.6. В одном баллоне вместимостью 15 дм3 находится газ под давлением 0,2 МПа, а в другом — тот же газ под давлением 1 МПа. Баллоны, температура которых одинакова, соединены трубкой с краном. Если открыть кран, то в обоих баллонах устанавливается давление 0,4 МПа. Какова вместимость второго баллона? 3.7. Открытая стеклянная колба вместимостью 0,40 дм3, содержащая воздух, нагрета до 127°С. Какой объем займет вода в колбе при остывании ее до 27°С, если после нагревания ее горлышко опустить в воду? 3.8. Объем пузырька воздуха по мере всплывания его со дна озера увеличился в 3 раза. Какова глубина озера? 3.9. При проведении опыта Торричелли внизу барометрической трубки образовался пузырек воздуха объемом 2 мм. Каким стал объем пузырька, если он поднялся и находится на расстоянии 1 см от уровня ртути в трубке?
Д3.3. В двух сосудах одинакового объема находятся гелий и аргон, массы которых равны. Во сколько раз давление гелия больше, чем аргона, если температуры газов одинаковы? Д3.4. К/р №1 - 1 4. Распределения Максвелла и Больцмана. 4.1. Определить среднюю арифметическую и наиболее вероятную скорости молекул газа, если известно, что их средняя квадратичная скорость равна 600 м/с. 4.2. Какова средняя арифметическая скорость молекул некоторого газа, если известно, что плотность его 30 г/м3, а давление, оказываемое им на стенки сосуда, 3,6 кПа? 4.3. Какая часть молекул азота при температуре 7°С обладает скоростями в интервале от 500 до 510 м/с? Найти наиболее вероятную скорость при этой температуре. Решить приближенно. 4.4. Определить отношение числа молекул водорода, обладающих скоростями в интервале от 2,0 до 2,1 км/с, к числу молекул, обладающих скоростями от 1,0 до 1,1 км/с, если температура водорода 0°С. К какому интервалу скоростей принадлежат 50% наиболее быстрых молекул? 30% наиболее быстрых? 30% наиболее медленных? Какая часть молекул имеет скорость, отличающуюся не более чем на 10% от наиболее вероятной (в обе стороны)? Воспользоваться графиком нормального распределения. 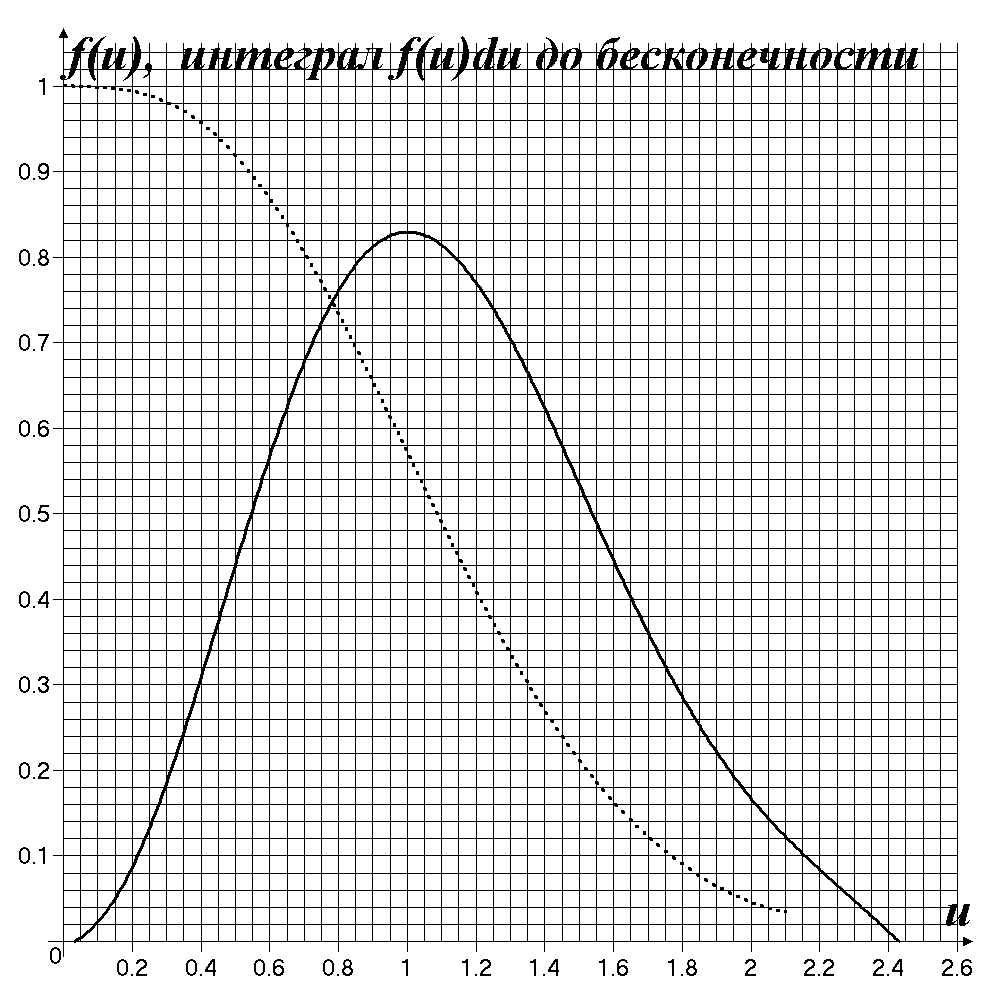 4.5. На поверхности Земли барометр показывает 101 кПа. Каково будет показание барометра при подъеме его на Останкинскую телевизионную башню, высота которой 540 м? Температуру считать всюду одинаковой и равной 7°С. 4.6. Оценить высоту вблизи поверхности земли, при подъеме на которую атмосферное давление уменьшается на 1 мм рт. ст. 4.7. Оценить перепад давления на крыше НГПУ и на дне оврага за НГПУ. 4.8. У поверхности Земли молекул водорода почти в 106 раз меньше, чем молекул азота. На какой высоте число молекул водорода будет равно числу молекул азота? Среднюю температуру атмосферы принять равной 0°С. 4.9. Пылинки массой 1 аг взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1,0%. Температуру воздуха во всем объеме считать одинаковой и равной 27°С. 4.10. В опыте Жака Перрена с помощью микроскопа изучалось распределение частиц гуммигута в водных эмульсиях в поле силы тяжести. Определить толщину слоя эмульсии, в котором концентрация частиц уменьшается в 2 раза, если плотность гуммигута 1006 кг/м3, а размер частиц составляет 0,5 мкм. Д4.1. При какой температуре средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на Δv= 50 м/с? Д4.2. Какая часть молекул кислорода при t= 0°С обладает скоростями от 100 до 110 м/с? От 900 до 1000 м/с? Д4.3. К/р №1 – 3, 4. 5. Работа. Внутренняя энергия. Первое начало термодинамики. 5.1. Отношение удельных теплоемкостей смеси, состоящей из нескольких молей азота и 5 молей аммиака, 1,35. Определить число молей азота в смеси. 5.2. В цилиндре диаметром d = 40 см содержится двухатомный газ объемом V = 80 дм3. На сколько следует увеличить нагрузку поршня при подводе количества теплоты Q = 84 Дж, чтобы поршень не пришел в движение? 5.3. Газ, для которого Сp/Сv=4/3, находится под давлением р = 0,20 МПа и занимает объем V1 =3,0 дм3. В результате изобарного нагревания объем его увеличился в 3 раза. Определить количество теплоты, переданное газу. 5.4. Изобразить в координатах p, V и p, T примерные графики изотермического и адиабатического процесса. 5.5. Двухатомный газ, находящийся при температуре 250°С, сжимают изотермически так, что его объем уменьшается в 3 раза. Затем газ расширяется адиабатно до начального давления. Найти температуру газа в конце адиабатного расширения. 5.6. В каком случае над идеальным газом при одинаковой степени его сжатия n = V1/V2 совершается большая работа: при изобарном, изотермическом или адиабатном процессе? 5.7. Двухатомный газ, занимающий объем 22 л под давлением 0,10 МПа, изобарно нагрет от 20 до 100°С. Определить работу, совершенную газом и приращение его внутренней энергии. 5.8. Расширяясь, трехатомный газ, состоящий из жестких (объемных) молекул, совершает работу 245 Дж. Какое количество теплоты было подведено к газу, если он расширяется: 1) изобарно; 2) изотермически? Д5.1. Определить для газовой смеси, состоящей из водорода массой 4,0 г и углекислого газа массой 22,0 г. Д5.2. Многоатомный газ, находящийся под давлением 0,10 МПа при температуре 7°С, был изобарно нагрет на 40 К, в результате чего он занял объем 8,0 дм3. Определить количество теплоты, переданное газу и увеличение его внутренней энергии. Д5.3. К/р №1 - 2 6. Термодинамика (продолжение)
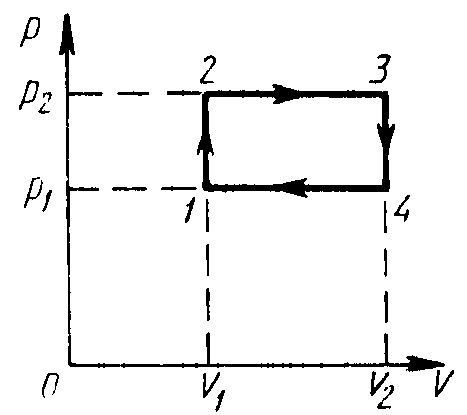
6.3. Расширяясь, трехатомный газ, состоящий из жестких (объемных) молекул, совершает работу 245 Дж. Какое количество теплоты было подведено к газу, если он расширяется: 1) изобарно; 2) изотермически? 6.4. Углекислый газ массой 4,4 г под давлением 0,10 МПа при температуре 87°С адиабатно сжимают до 1/20 его начального объема. Определить конечную температуру и давление газа, приращение внутренней энергии и работу, совершенную газом. 6.5. Какой объем сжатого двухатомного газа нужно израсходовать для совершения работы 250 кДж, если при адиабатном расширении объем его увеличивается в 2 раза при начальном давлении 0,18 МПа? 6.6. В цилиндре под поршнем находится 1 моль двухатомного газа при температуре 27°С. Сначала газ расширяется адиабатно так, что его объем увеличивается в 5 раз, а затем сжимается изотермически до первоначального объема. Определить совершенную газом работу. 6.7. Волейбольный мяч массой m = 200 г и объемом V = 8,0 дм3 накачан до избыточного давления 20 кПа. Мяч был подброшен на высоту h= 20 м и после падения на твердый грунт подскочил почти на ту же высоту. Оценить максимальную температуру воздуха в мяче в момент удара о грунт. Температура наружного воздуха 300 К. 6.8. Газ объемом 50 л, находящийся под давлением 0,30 МПа, нагревают при постоянном объеме до тех пор, пока давление его увеличится в 2 раза, после чего газ изотермически расширяется до начального давления, и, наконец, его охлаждают при постоянном давлении до начального объема. Определить работу, совершенную газом в каждом из этих процессов.
Д6.1. 10 г кислорода находятся в сосуде под давлением р = 300 кПа и температуре 10°С. После изобарического нагревания газ занял объем V= 10 л. Найти количество теплоты, полученное газом, изменение внутренней энергии газа и работу, совершенную газом при расширении. Д6.2. При изотермическом расширении 10 г азота, находящегося при температуре 17°С, была совершена работа 860Дж. Во сколько раз изменилось давление при расширении? Д6.3. При адиабатическом сжатии воздуха в цилиндрах двигателя внутреннего сгорания давление изменяется от р1= 0,1 МПа до р2 = 3,5 МПа. Начальная температура воздуха t1 = 40 °С. Найти температуру воздуха в конце сжатия. 7. Тепловые двигатели. Цикл Карно 7.1. Газ, совершающий цикл Карно, 3/4 теплоты, полученной от нагревателя, отдает холодильнику. Температура холодильника 0°С. Определить температуру нагревателя. Найти КПД этого цикла.
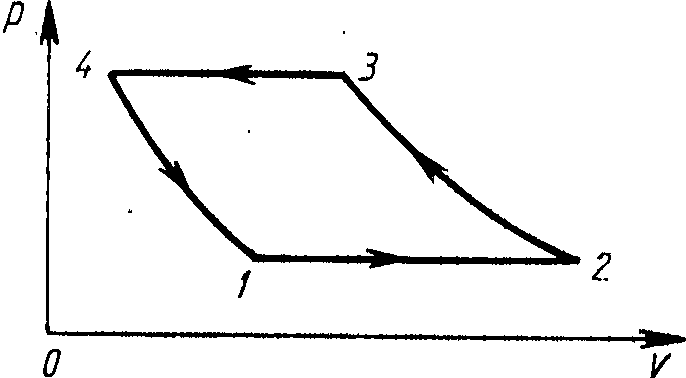
7.4. Идеальный двухатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причем наибольшее давление в 3 раза больше наименьшего, а наибольший объем в 5 раз больше наименьшего. Определить КПД цикла. 7.5. Наименьший объем газа, совершающего цикл Карно, 12 л. Определить наибольший объем, если объем газа в конце изотермического расширения 60 л, в конце изотермического сжатия — 19 л. 7.6. КПД паровой машины составляет 50% от КПД идеальной тепловой машины, которая работает по циклу Карно в том же интервале температур. Температура пара, поступающего из котла в паровую машину, 227°С, температура в конденсаторе 77°С. Определить мощность паровой машины, если она за 1 ч потребляет уголь массой 200 кг с теплотворной способностью 31 МДж/кг. 7.7. Двухатомный газ совершает цикл Карно, причем при изотермическом расширении его объем увеличивается в 2 раза, а при последующем адиабатном расширении он производит работу 300 кДж. Определить работу, совершаемую газом за один цикл.
Д7.1. Идеальная тепловая машина, работающая по циклу Карно, имеет температуру нагревателя 227°С, температуру холодильника 127°С. Во сколько раз нужно увеличить температуру нагревателя, чтобы КПД машины увеличился в 3 раза? Д7.2. Идеальная тепловая машина Карно совершает за один цикл работу А = 2,94 кДж и отдает за один цикл холодильнику количество теплоты Q= 13,4 кДж. Найти КПД машины. Д7.3. Идеальная тепловая машина Карно за цикл получает от нагревателя количество теплоты Q1 = 2,512 кДж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 — 300 К. Найти работу, совершаемую машиной за один цикл, и количество теплоты Q2, отдаваемое холодильнику за один цикл. 8. Реальные циклы. Холодильные машины.
8.3. В комнате открыли работающий холодильник. Как изменилась температура в комнате? 8.4. Тепловую машину, работающую по циклу Карно с КПД = 20%, используют при тех же условиях как холодильную машину. Найти ее холодильный коэффициент. 8.5. Холодильник мощностью Р за время превратил в лед п литров воды, которая первоначально имела температуру t°C. Какое количество теплоты выделилось в комнате за это время? 8.6. В идеальной холодильной машине, работающей по обратному циклу Карно, совершается перенос теплоты от тела с температурой —- 20°С к воде, имеющей температуру 10°С. Определить, какое количество теплоты будет отнято от охлаждаемого тела за один цикл, если известно, что данная холодильная машина приводится в действие с помощью тепловой машины Карно, которая работает в интервале температур 202—107°С и передает за каждый цикл холодильнику 504 кДж теплоты. Д8.1. В цикле двигателя внутреннего сгорания, рассмотренном в задаче 8.1, горючая смесь, которую можно считать двухатомным газом с жесткими молекулами, сжимается до объема 2 л. Ход и диаметр поршня равны соответственно 40 и 15 см. Определить КПД цикла. Д8.2. Домашний холодильник потребляет ток средней мощностью 40 Вт. Какое количество теплоты выделится в комнате за сутки, если холодильный коэффициент = 9? Д8.3. К/р №2 - 1 9. Макро- и микросостояния. Энтропия. 9.1. В сосуде содержится 5 молекул. Определить вероятность состояния, при котором в правой половине сосуда находиться 2 молекулы. Чему равна вероятность состояния, при котором либо в левой, либо в правой половине сосуда находятся 2 молекулы? Каков статистический вес этого состояния? 9.2. Некоторая термодинамическая система перешла из состояния 1 в состояние 2. Статистический вес второго состояния превосходит статистический вес первого состояния в 2раза. Чему равно приращение энтропии системы ? 9.3. Статистический вес состояния некоторой массы газа равен Ω1. Определить статистический вес Ω2 состояния в γ раз большей массы того же газа. Температура и давление газа в обоих случаях одинаковы. 9.4. Гелий в количестве 1 моль, изобарно расширяясь, увеличил свой объем в 4 раза. Найти приращение энтропии при этом расширении. 9.5. Воздух массой 1,0 кг сжимают адиабатно так, что объем его уменьшается в 6 раз, а затем при постоянном объеме давление возрастает в 1,5 раза. Определить приращение энтропии в этом процессе. 9.6. Определить приращение энтропии углекислого газа массой 1,0 кг в процессе сжатия от давления 0,20 МПа при температуре 40°С до давления 4,5 МПа при температуре 253°С. 9.7. Энтропия термодинамической системы в некотором состоянии равна 3,18 мДж/К. Чему равен статистический вес этого состояния системы? 9.8. Кислород массой 1,0 кг при давлении 0,50 МПа и температуре 127°С, изобарно расширяясь, увеличивает свой объем в 2 раза, а затем сжимается изотермически до давления 4,0 МПа. Определить суммарное приращение энтропии. 9.9. Определить приращение энтропии при смешении азота массой 3,0 кг и углекислого газа массой 2,0 кг. Температуры и давления газов до смешения одинаковы. 9.10. Идеальный газ в количестве 1 моль изотермически расширяется так, что при этом происходит приращение энтропии на 5,75 Дж/К. Определить натуральный логарифм отношения термодинамических вероятностей начального и конечного состояний газа, а также отношение начального и конечного его давлений. Д9.1. Энтропия термодинамической системы в некотором состоянии равна 3,18 мДж/К. Чему равен статистический вес этого состояния системы? Д9.2. До какой температуры нужно довести кислород массой 4,0 кг, находящийся при температуре 227°С, не меняя его объема, чтобы уменьшить энтропию кислорода на 1,31 кДж/К? Д9.3. Найти изменение энтропии Sпри превращении 1кг воды (Т1 = 273 К) в пар (Т2 = 373 К). 10. Длина свободного пробега. Явления переноса. 10.1. В межзвездном пространстве содержится 1 молекула в объеме 15 см3. Какова средняя длина свободного пробега молекул, если предположить, что окружающие молекулы являются молекулами водорода? 10.2. Средняя длина свободного пробега молекул воздуха при нормальном давлении 62,1 нм. Определить среднюю длину свободного пробега молекул воздуха при сверхвысоком вакууме (1,33 нПа). Температуру считать одной и той же. 10.3. Какое давление нужно создать в колбе диаметром 0,10 м, содержащей азот при температуре 20°С, чтобы получить вакуум? 10.4. Сколько столкновений за 1,0 с испытывают молекулы углекислого газа, находящегося при нормальных условиях? 10.5. Средняя длина свободного пробега молекул гелия при нормальных условиях 0,23 мкм. Определить коэффициент диффузии гелия при этих условиях. 10.6. Рассчитать коэффициенты диффузии для водорода и кислорода при нормальных условиях. 10.7. Для гелия динамическая вязкость при температуре 0°С равна 16,3 мкПа·с. Определить диаметр молекул гелия. 10.8. Найти динамическую вязкость воздуха при температуре 100°С и нормальном давлении, если при нормальных условиях она равна 17,2 мкПас. 10.9. Два тонких узких кольца расположенные в воздухе при нормальных условиях друг над другом и могут вращаться. Одно из колец приводится во вращение с частотой 20 об/с. Определить силу, действующую на второе кольцо, если расстояние между кольцами 0,5 см, средний радиус колец 10 см, ширина колец 1 см. 10.10. Внутренний цилиндрический сосуд калориметра имеет высоту 10 см и радиус 5 см. Расстояние между внутренней и наружной стенками калориметра 1 см. В калориметр налили доверху воду при температуре 50°С. Через какое время вода в калориметре остынет на 10°С? Теплоёмкостью калориметра, теплопроводностью изолирующей крышки и стенок калориметра пренебречь. 10.11. Вычислить, какое количество тепла уходит за сутки через окна. Воспользоваться параметрами окон помещения, в котором проходят занятия. Температура на улице –20°С, в помещении 20°С. Какое количество угля нужно сжечь, чтобы скомпенсировать тепловые потери? Уголь имеет теплотворную способность 31 МДж/кг. Эффективный диаметр некоторых молекул
Д10.1. В баллоне вместимостью 10 дм3 находится гелий массой 2,0 г. Определить среднюю длину свободного пробега молекул гелия. Д10.2. Определить коэффициенты диффузии азота и аргона при нормальных условиях. Д10.3. Определить теплопроводность хлора, если известно, что динамическая вязкость для него при этих условиях равна 12,9 мкПас. Д10.4. К/р №2 - 2 11. Реальные газы. Критическое состояние. 11.1. В баллоне вместимостью 22 литров находится азот массой 1,40 кг, при температуре 0°С. Определить давление газа на стенки баллона, внутреннее давление газа и собственный объем молекул. Для азота а = 0,136 Джм3/моль2, b = 410-5 м3/моль. 11.2. Найти диаметр молекулы аргона по известной постоянной bв уравнении Ван-дер-Ваальса. Для аргона b = 310-5 м3/моль. 11.3. Какова масса воды, налитой в сосуд вместимостью 30 см3, при которой ее можно привести в критическое состояние путем нагревания запаянного сосуда с водой? Для воды Тк = 647 К, Pк = 22 МПа. 11.4. Найти значения постоянных, а и bдля бензола (С6Н6) в уравнении Ван-дер-Ваальса по известным для него значениям критических температуры Тк и давления Pк. Для бензола Тк = 562 К, Pк = 4,8 МПа. 11.5. Каково внутреннее давление углекислого газа в момент сжижения, если при этом его плотность 550 кг/м3, а также известны критические температура Тк = 304 К и давление Pк = 7,4 МПа? 11.6. Определить среднюю длину свободного пробега молекул аргона при нормальных условиях, если для него известны критические температура Тк = 151 К и давление Pк = 4,87 МПа. 11.7. В сосуде, объемом V = 10л находится масса т = 0,25 кг азота при температуре t = 27 °С. Какую часть давления газа составляет давление, обусловленное силами взаимодействия молекул? Какую часть объема сосуда составляет собственный объём молекул? Для азота а = 0,136 Джм3/моль2, b = 410-5 м3/моль. Д11.1. Каково давление углекислого газа при температуре 3°С, если его плотность при этой температуре 550 кг/м? Рассчитать по уравнению Ван-дер-Ваальса. Для углекислого газа а = 0,364 Джм3/моль2, b = 4,310-5 м3/моль. Д11.2. Определить диаметр молекулы кислорода по известным для него значениям критических температуры Тки давления Pк. Для кислорода Тк = 154 К, Pк = 5,07 МПа. Д11.3. Найти плотность гелия в критическом состоянии, считая известными для него Тк = 5,2 К, Pк = 0,28 МПа. Д11.4. К/р №2 - 4 12. Влажность. 12.1. Полированный металлический предмет занесли в помещение с улицы и он покрылся конденсатом (запотел). Определить наибольшую температуру воздуха снаружи помещения, если в помещении 20oC и относительная влажность 60 %. 12.2. Сколько молекул водяного пара содержится в комнате вместимостью 150 м3 при температуре 20°С и относительной влажности 30%? 12.3. Воздух объемом 1 м3 находится при температуре 20°С и относительной влажности 50%. Какова масса выпавшей росы, если, не меняя температуру воздуха, уменьшить его объем в 3 раза? 12.4. Воздух объемом 1 м3 первоначально находился при температуре 20°С и относительной влажности 60%. Затем воздух охладили до 5°С. Каковы масса выпавшей росы и плотность водяного пара при этой температуре? Давление насыщенных паров воды при 20°С равно 2338,1 Па, при 5°С – 871,1 Па. 12.5. Найти массу влажного воздуха объемом 1,0 м3 при температуре 29°С, относительной влажности 60% и нормальном атмосферном давлении. Какова масса водяного пара, содержащегося в воздухе при данных условиях в аудитории? (Объем аудитории оценить самостоятельно). 12.6. Относительная влажность воздуха, находящегося в сосуде при температуре 20°С, равна 70%. На сколько изменится относительная влажность воздуха, если его нагреть до 100°С, уменьшив при этом объем в 2 раза? 12.7. В сосуд объема V= 10 л поставили блюдце, содержащее т = 1 г воды. После этого сосуд герметически закрыли и оставили при температуре 20°С, при которой давление насыщенного пара р = 2,33 кПа. Какая часть воды испарится? Таблица давления насыщенных паров воды  Д12.1. Воздух находился при температуре 10°С и относительной влажности 60%. На сколько увеличилась масса водяных паров в 1 м3 воздуха при нагревании его до 20°С, если относительная влажность осталась неизменной? Давление насыщенных паров воды при 20°С равно 2338,1 Па, при 5°С – 1227,7 Па. Д12.2. Какая масса т водяного пара содержится в объеме V = 1 м3 воздуха в летний день при температуре t= 30°С и относительной влажности 75%? Д12.3. Смешали 1 м3 воздуха с относительной влажностью 20% и 2 м3 воздуха с относительной влажностью 30%. При этом температура воздуха была одинакова. Смесь занимает объем 3 м3. Определить ее относительную влажность. 13. Поверхностное натяжение. 13.1. Рамка с подвижной нижней перекладиной длиной 15 см затянута мыльной пленкой. Какую надо совершить работу против сил поверхностного натяжения, чтобы растянуть пленку на 4 см, если коэффициент поверхностного натяжения (КПН) равен 45 мН/м? 13.2. Вычислить разность уровней воды в капиллярах диаметром 0,5 и 1 мм, которые погружены в сосуд с водой. Какова была бы разность уровней, если бы капилляры погрузили в сосуд с ртутью? КПН воды 72 мН/м. 13.3. Определить работу, необходимую для превращения воды массой 1 г в туман, т. е. для распыления ее в капельки диаметром 0,20 мкм. 13.4. Определить добавочное давление и плотность воздуха внутри мыльного пузыря диаметром 1,0 см при температуре 20°С. Поверхностное натяжение мыльной воды 45 мН/м. 13.5. В стеклянную трубку с внутренним диаметром 20 мм вставлена коаксиально стеклянная палочка диаметра 19мм. Считая смачивание полным, определить высоту капиллярного поднятия воды в кольцевом зазоре между трубкой и палочкой. 13.6. Капля ртути массой 1,36 г введена между параллельными стеклянными пластинами. Какую силу нужно приложить для того, чтобы расплющить каплю до толщины 0,1 мм? Несмачивание считать полным. 13.7. После покрытия слоем парафина радиус отверстий решета стал равен 1,5 мм. Приняв во внимание, что вода не смачивает парафин, определить высоту hслоя воды, который можно носить в решете так, чтобы вода не пролилась через отверстия. 13.8. Какова будет высота столба ртути в барометрической трубке диаметром 2 мм, если атмосферное давление 0,1 МПа? Каков должен быть минимальный диаметр барометрической трубки, чтобы поправка на поверхностное натяжение не превышала 13,3 Па? Д13.1. На какую высоту поднимается под действием капиллярных сил вода в образовавшихся в почве капиллярах диаметром 0,3мм и в стеблях ржи, имеющих средний диаметр пор 20 мкм? Смачивание считать полным. Д13.2. Какую работу против сил поверхностного натяжения надо совершить, чтобы разделить сферическую каплю ртути радиусом 3 мм на две одинаковые капли?
14. Жидкости. Кипение. Уравнение Клайперона-Клаузиуса. Осмос. 14.1. Каково атмосферное давление, если вода кипит при температуре 95°С? Удельные объемы воды и пара равны соответственно 1,04 дм3/кг и 1,67 м3/кг. 14.2. На горе вода кипит при температуре 80°С. Пользуясь барометрической формулой и таблицей насыщенных паров воды, определить высоту горы. Температуру воздуха считать постоянной. 14.3. Пользуясь уравнением Клаузиуса — Клапейрона и данными таблицы насыщенных паров воды, найти удельную теплоту парообразования r воды при температуре 5°С. 14.4. В закрытом сосуде вместимостью 4 л находится вода массой 2 кг при температуре 373 К. На сколько нужно повысить температуру системы, чтобы масса насыщенного пара, находящегося над водой, увеличилась на 1,6 г? 14.5. До какой температуры был нагрет насыщенный водяной пар, находящийся при температуре 50°С, если давление его увеличилось в 8 раз? 14.6. Сосуд вместимостью 1,0 дм3, изготовленный из полупроницаемого вещества, наполнен водой, которая содержит поваренную соль массой 0,20 г, и опущен в воду. На сколько вследствие осмотического давления поднимется уровень в узкой трубке, вставленной в полупроницаемый сосуд, если при температуре 27°С все молекулы соли диссоциированы? 14.7. Поваренная соль массой 3 г растворена в воде объемом 1 дм3 при температуре 30°С. Осмотическое давление при этих условиях оказалось 0,17 МПа. Какова степень диссоциации молекул соли? Д14.1. Каково осмотическое давление раствора, если в нем на одну молекулу растворенного вещества приходится 800 молекул воды? Температура раствора 47°С. Диссоциация отсутствует. 15. Твердые тела. Тепловые свойства твердых тел. Фазовые переходы. 15.1. Концы стального стержня сечением 5 см2 наглухо закреплены в двух стенах. Какова сила, действующая на стены при температуре 20°С, если при 10°С стержень находился в ненапряженном состоянии? Модуль Юнга стали 210 ГПа, коэффициент теплового расширения 1,06 ·10–5 К–1. 15.2. Найти зависимость периода свободных колебаний от температуры для однородного твердого тела вокруг горизонтальной оси, не проходящей через его центр тяжести. 15.3. Вычислить по классической теории теплоемкости удельные теплоемкости кристаллов: 1) алюминия; 2) меди; 3) платины. Плотности соответственно 2600, 8600 и 21400 кг/м3. 15.4. Определить приращение энтропии при затвердевании ртути массой 1 кг при температуре затвердевания –38,9°С. Удельная теплота кристаллизации ртути 11,7 кДж/кг. 15.5. Определить температуру плавления льда при давлении 1 МПа. Считать, что при изменении давления в пределах от 0,10 до 1,0 МПа плотность льда и воды и удельная теплота плавления постоянны. Удельная теплота плавления льда 334 кДж/кг, плотность льда 900 кг/м3, воды – 1000 кг/м3. 15.6. Струя водяного пара при температуре 100°С, направленная на глыбу льда массой 4,0 кг при температуре –20°С, растопила ее и нагрела получившуюся воду до 60°С. Найти приращение энтропии при этом процессе. Удельная теплота парообразования воды 2,26 МДж/кг, удельная теплота плавления льда 334 кДж/кг, теплоемкость льда 2100 Дж/(кг·К), воды – 4190 Дж/(кг·К). 15.7. Толщина деревянной стены 10 см. Какой должна быть толщина кирпичной стены, чтобы она обладала такой же теплопроводностью, как деревянная? Коэффициенты теплопроводности соответственно 0,84 и 0,17 Вт/(м·К). 15.8. Две пластины – медная и железная – одинаковой толщины вплотную прилегают друг к другу. Температура наружной поверхности медной пластинки 100°С, железной – 0°С. Найти температуру в месте соприкосновения пластин. Коэффициенты теплопроводности меди и железа соответственно 390 и 62 Вт/(м·К). 15.9. Сколько угля необходимо сжечь в комнате, чтобы восполнить потери тепла через стены за сутки? Температура за окном –20°С, в комнате 20°С, уголь имеет теплотворную способность 31 МДж/кг. Воспользоваться параметрами помещения, в котором проходят занятия. Д15.1. К стальной проволоке радиусом 1 мм подвешен груз. Под действием этого груза проволока получила такое же удлинение, как при нагревании на 20°C. Найти массу груза. Данные для стали см. задачу 15.1. Д15.2. Пользуясь законом Дюлонга и Пти, найти, из какого материала сделан металлический шарик массой 0,025 кг, если известно, что для его нагревания от10°С до 30°С потребовалось затратить количество теплоты 117Дж. (См. таблицу теплоемкостей.) Д15.3. Свинцовая пуля, летящая со скоростью 400 м/с, ударяется о стенку и входит в нее. Считая, что 10% кинетической энергии пули идет на ее нагревание, найти, на сколько нагрелась пуля. Молярную теплоемкость свинца найти по закону Дюлонга и Пти. | ||||||||||||||||||||||||||||||||||||||||||