Молекулярная (статистическая) физика и термодинамика

• Название: Молекулярная (статистическая) физика и термодинамика
• Дата: 15.02.2019
• Размер: 404.37 Kb.
• Имя файла: 2razdel.docx
• Тип: Документы; #67704

РАЗДЕЛ 2. МОЛЕКУЛЯРНАЯ (статистическая) физика и термодинамика
1)Равновесное состояние системы. Равновесный процесс. Уравнение состояния идеального газа, смеси газов.

Термодинамическая система называется равновесной (обратимой), если всепараметры состояния системы имеют определенные значения.

Изолированные системы со временем неизбежно и самопроизвольнопереходят в равновесное состояние (состояние теплового равновесия) иникогда из него самопроизвольно выйти не могут.

Все количественные выводы термодинамики применимы только кравновесным состояниям и обратимым процессам.

Равновесный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными.

Газ, взаимодействием молекул которого можно пренебречь, называетсяидеальным.

Соотношение, определяющее связь между параметрами состояния какого-либо тела, называется уравнением состояния этого тела.F(p,V,T) = 0

Соотношение между параметрами состояния для идеального газа -уравнение Менделеева-Клапейрона.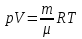

μ – молярная масса газа.

R – универсальная (молярная) газовая постоянная (8,31Дж/(моль*К))

Число молекул в газе массой m: ,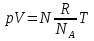

k – постоянная Больцмана:

pV = NkT, p = nkT

– число молекул в единице объема газа, т.е. концентрация.
2)Физические основы термодинамики. Теплота, работа, внутренняя энергия.

Работой называется обобщенная форма обмена энергией между системой и окружающей средой, в основе которой лежит изменение внешних параметров системы.

Элементарной работой A называется работа, совершённая системой в ходе элементарного процесса. Элементарная работа определяется формулой A = pdV,

где p – давление газа, dV – бесконечно малое изменение объёма системы.

Если газ расширяется, то dV>0. Элементарная работа газа A>0. Газ совершает работу. Если газ сжимается, то dV<0 и A<0. Над газом совершается работа.
dV - бесконечно малое изменение объёма системы. Функция процессапервого типа;

A - элементарная работа, бесконечно малая величина. Функция процессавторого типа.

Символ d означает бесконечно малое изменение, а символ – бесконечномалую порцию.

Работа системы в ходе произвольного процесса:

Работа над системой:

Энергия, которую получает система при теплообмене с окружающей средой, называется теплом (количеством теплоты).

Если Q>0, то система получает энергию из окружающей среды, если Q<0, тосистема отдаёт энергию в окружающую среду.

РАБОТА И ТЕПЛОТА – НЕ ВИДЫ ЭНЕРГИИ, А ФОРМЫ ЕЕ ОБМЕНА.

Сумма кинетических энергий хаотического движения всех частиц тела относительно центра масс тела (молекул, атомов) и потенциальных энергий их взаимодействия друг с другом называется внутренней энергией.

i – число степеней свободы (3-одноатомный, 5-двухатомный, 6-многоатомный)

3)Первое начало термодинамики. Работа при расширении и сжатии газа. Графическое изображение термодинамических процессов и работы.

В каждом элементарном процессе теплоQ, приобретённое системой,расходуется на увеличение внутренней энергии системы dU и работуA,совершаемую системой в этом процессе:Q = dU +A

1. Изохорный процесс. V=const.

Работа A=0

ТеплоA=0

Сообщаемое системе тепло превращается в её внутреннюю энергию: Q=dU.

Внутренняя энергия идеального газа, удалённого от силовых полей, естьсредняя суммарная кинетическая энергия всех его молекул.

В изохорном процессе единственным способом изменения внутренней энергии системы является теплообмен.
Тепло: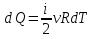

2. Изобарный процесс. Р=const.

Работа:

При изобарном расширении V>0, и газ совершает положительную работу, тратя на это свою внутреннюю энергию.

При изобарном сжатии V<0, и работа газа отрицательна, то есть работа совершается внешним объектом над газом, и газ при этом получает извне добавку к своей внутренней энергии.

В изобарном процессе теплоёмкость газа не зависит от температуры -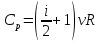

Тепло: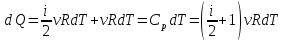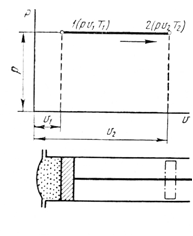

3. Изотермический процесс. Т=const.

Работа: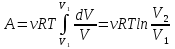

В изотермическом процессе только тепло является источником работы.

В работу превращается всё подводимое к газу тепло.

Тепло: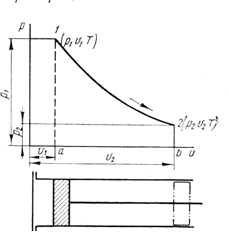



4. Адиабатический процесс.



Зависимость p(V) следует из уравнения Пуассона pV^y = const



При адиабатном расширении работа положительна (её совершает газ), при сжатии – отрицательна (её совершает над газом внешняя сила).



Используя уравнение Пуассона, можно связать работу с относительным изменением давленияp₁/p₂в виде:

Тепло: По определению адиабатического процесса система в этом процессе не получает и не отдаёт тепло, так что:

4)Теплоёмкость вещества.

Теплоемкость - количество теплоты необходимое для нагревания тела на один Кельвин:

Удельной теплоемкостью называется величина, числено равная теплоте, которую надо сообщить единице массы тела для повышения его температуры на один Кельвин: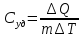



Отсюда можно определить количество теплоты, необходимое для нагревания вещества, массы m:

Молярная теплоемкость - количество тепла необходимое для нагревания одного моля вещества на один Кельвин:

Воспользовавшись I законом термодинамики выражение (1) можно переписать в виде:



Откуда следует, что теплоемкость есть функция процесса, т.е. теплоемкость системы зависит от того каким образом система переходит из одного состояния в другое. Вообще говоря, таких процессов может быть сколько угодно, фактически же используются чаще всего теплоемкость при р=const(C_p) и при V=const(C_v).

5)Изохорический процесс. Изобарический процесс.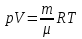


Изохорический (изохорный) процесс – процесс, происходящий в физическойсистеме при постоянном объеме.

В идеальном газе при изохорическом процессе давление пропорциональнотемпературе – законШарля. (V = const)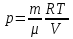



Изобарический (изобарный) процесс – процесс, происходящий в физической системе при постоянном внешнем давлении.

Объем идеального газа при изобарическом процессе пропорционален

температуре – закон Гей-Люссака. (p = const)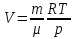



6)Изотермический процесс. Адиабатический процесс.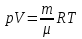



Изотермический процесс – процесс, происходящий в физической системепри постоянной температуре.

В идеальном газе при изотермическом процессе произведение давления наобъем постоянно – закон Бойля-Мариотта.(T = const)



Адиабатический процесс – процесс, происходящий в физической системе без теплообмена с окружающей средой.

При быстром адиабатическом сжатии газ не успевает отдать выделившуюся теплоту и сильно нагревается.

Адиабатическое расширение газа вызывает его охлаждение.

Уравнения адиабаты:

1. В переменных T, Vуравнение выглядит так: TV^y-1 = const

2. В переменных p, Vуравнение выглядит так:pV^y= const

3. В переменных p, Tуравнение выглядит так:T^yp^1-y= const

Адиабатическая постоянная или показатель адиабаты:
7)Число степеней свободы. Закон распределения энергии по степеням свободы. Внутренняя энергия.

Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета.

Например, положение материальной точки в пространстве определяется тремя координатами x, y, z, следовательно, материальная точка обладает тремя степенями свободы.

У одноатомной молекулы i = 3, тогда для одноатомных молекул

для двухатомных молекул

для трёхатомных молекул

Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится

кинетическая энергия движения частиц и потенциальная энергия их взаимодействия составляют внутреннюю энергию тела. Внутреннюю энергию обозначают  и измеряется она, как и все другие виды энергии, в Дж (джоулях).

8)Барометрическая формула. Закон Больцмана для распределения частиц во внешнем потенциальном поле.

Барометрическая формула — зависимость Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести в стационарных условиях.

Для идеального газа, имеющего постоянную температуру {\displaystyle T} и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения {\displaystyle g} одинаково), барометрическая формула имеет следующий вид:

{\displaystyle p=p_{0}\exp \left[-Mg{\frac {h-h_{0}}{RT}}\right],}

 или плотности газа от высоты в поле силы тяжести в стационарных условиях.

Для идеального газа, имеющего постоянную температуру {\displaystyle T} и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения {\displaystyle g} одинаково), барометрическая формула имеет следующий вид:

{\displaystyle p=p_{0}\exp \left[-Mg{\frac {h-h_{0}}{RT}}\right],}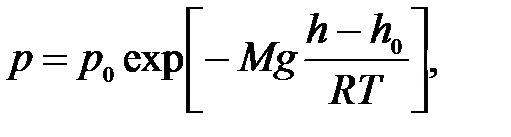



Где p {\displaystyle p}Ppp  — давление газа в слое, расположенном на высоте {\displaystyle h}h,p₀ {\displaystyle p_{0}}p0— давление на нулевом уровне (h=h₀{\displaystyle h=h_{0}}), {\displaystyle M}M — молярная масса газа.{\displaystyle T}T — абсолютная температура.

9) Распределение молекул идеального газа по абсолютным значениям скоростей и по компонентам скоростей (распределение Максвелла). Характерные скорости.

Распределение проекции скорости молекулы является нормальным:


Распределение молекул по абсолютным значениям скоростей :


Характерные скорости:

Наиболее вероятная скорость v_ВЕР — это скорость, отвечающая максимальному значению функции распределения.

Средняя арифметическая скорость  — это отношение суммы абсолютных величин скоростей всех молекул в системе к числу этих молекул.

Среднеквадратичная скорость — это корень квадратный из среднего значения квадрата скорости молекул

10)Распределение Максвелла в приведенном виде

Решение ряда задач удобнее проводить, если выражать скорости молекул в относительных единицах — единицах наиболее вероятной скорости . Тогда относительная скорость молекулы/

Распределение Максвелла в приведенном виде через u:


11)Распределение Максвелла по кинетическим энергиям частиц


12)Распределение Максвелла-Больцмана

 закон Максвелла даёт распределение частиц по значениям кинетической энергии, а закон Больцмана – распределение частиц по значениям потенциальной энергии. Оба распределения можно объединить в единый закон Максвелла – Больцмана:

.

Где n₀ - число молекул в единице объёма в той точке, где U = 0, E = U+K – полная энергия. 
13)Обратимые и необратимые процессы, круговые процессы (циклы). Прямой цикл Карно

Обратимый процесс — равновесный термодинамический процесс, который может проходить как в прямом, так и в обратном направлении.
Необратимый термодинамический процесс - термодинамический процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения
Круговым процессом, или циклом, называется такой процесс, в результате которого термодинамическое тело возвращается в исходное состояние
Цикл Карно - обратимый круговой процесс, в котором совершается наиболее полное превращение теплоты в работу (или работы в теплоту). Термический КПД и холодильный коэффициент цикла Карно не зависят от физических свойств рабочего тела. Прямой (обратный) цикл Карно имеет максимально возможный термический КПД (холодильный коэффициент) в заданном интервале температур.


Два процесса 1-2 и 3-4 (рис. 6.2) протекают при постоянных температурах, причем Т₁- температура горячего источника (нагревателя), Т₂ – температура холодного источника (холодильника, т.е. Т₁Т₂. Процессы 2-3 и 4-1 – адиабатные
14)Второе начало термодинамики. Энтропия
Второе начало термодинамики - в изолированной системе энтропия остаётся либо неизменной, либо возрастает (в неравновесных процессах), достигая максимума при установлении термодинамического равновесия (закон возрастания энтропии).

Энтропия -мера необратимого рассеивания энергии, мера отклонения реального процесса от идеального.

С точки зрения термодинамики энтропия – это такая функция состояния системы, изменение которой dS в элементарном равновесном процессе равно отношению порции тепла δQ, которое система получает в этом процессе, к температуре системы T: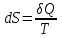



15)Вычисление Энтропии в различных процессах : энтропия идеального газа

изохорический: т.к. 

изобарический: т.к. Р₁ = Р₂

изотермический:  т.к. ;

При V2>V1 (расширение) энтропия растёт, при V2

Энтропия в процессе изотермического расширения увеличивается, а в процессе изотермического сжатия уменьшается

Адиабатический :  , т.к. 

Адиабатический процесс является изоэнтропийным.

Энтропия идеального газа :

16)Микро и Макросостояния. Статистический вес, термодинамическая вероятность макросистемы. Статистическое толкование энтропии

Макросостояние- состояние макроскопического тела (т.е тела, образованного огромным количеством молекул) с помощью таких параметров, как объем,давление,температура,внутр. Энергия и др.
Микросостояние- состояние макроскопического тела, охарактеризованное настолько подробно, что оказывается заданными сост. Всех образующих тело молекул.
Количество возможных микросостояний системы, находящейся в некотором макросостоянии, называется статистическим весом макросостояния.

Статистический вес Ω - функция макросостояния.

термодинамическая вероятность -  число микросостояний (микрораспределений, например, распределений молекул по пространству или энергии) которыми может определяться рассматриваемое макрораспределение.

Число распределений можно подсчитать следующим образом:



где общее число молекул,число молекул в 1 – ой части сосуда,во второй.

Связь энтропии с вероятностью была установлена Больцманом, постулировавшим, что энтропия пропорциональна логарифму вероятности состояния

,

(энтропия определяется с точностью до константы

const), где константа Больцмана,термодинамическая вероятность