дискретная математика. Московский энергетический институт
 Скачать 126.71 Kb. Скачать 126.71 Kb.
|
|
Научно-исследовательский университет МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ Институт дистанционного и дополнительного образования Письменная работа Темы 4-6 Выполнил: студент <>_<> Принял: преподаватель <>_<> Задание 6.Найдите число перестановок элементов 1,..., m, оставляющих ровно k элементов неподвижными. Решение N=3, m=4, k=1 Вариантов неподвижных точек: 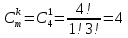 В каждом из этих вариантов остальные 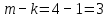 образуют перестановки. образуют перестановки.Число перестановок из 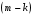 элементов всего: элементов всего: 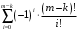 . . Искомое число перестановок равно: 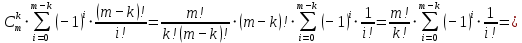 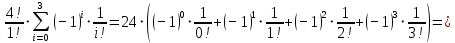 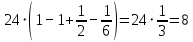 Ответ: 8. Задание 7.1) Постройте матрицы смежности и инциденций графа. 2) Постройте эйлеров и гамильтонов циклы или докажите, что соответствующий цикл не существует. 3) Найдите хроматическое число и оптимальную раскраску вершин графа. Все графы имеют множество вершин {1,2,3,4,5,6}. Ребра определяются в варианте задания. Для краткости они указываются без скобок и запятых. Ребра 12, 14, 24, 25, 35, 36, 45, 56. Решение: Граф 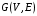 имеет 6 вершин имеет 6 вершин 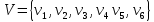 и 8 ребер и 8 ребер 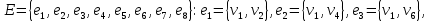 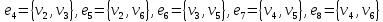 . .Построим граф: 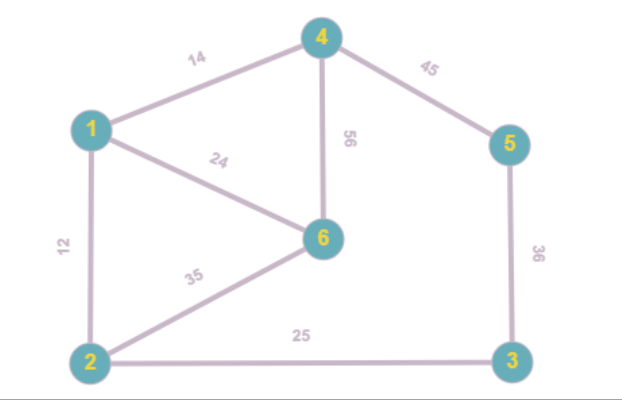 Построим матрицу смежности 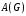 и матрицу инциденций и матрицу инциденций 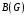 данного графа данного графа 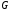 : :Матрица смежности: 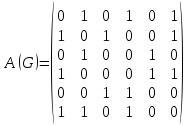 Матрица инциденций: 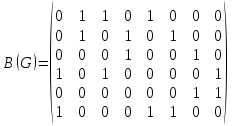 2) Эйлеров цикл не существует, так как не выполняется второе требование Теоремы 2 (стр. 37) - «степень каждой вершины четна». А в данном графе 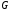 степени вершин степени вершин 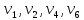 - нечетны. - нечетны.Гамильтонов цикл существует. Цикл - 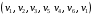 является гамильтоновым циклом, так как проходит ровно один раз через каждую вершину графа. является гамильтоновым циклом, так как проходит ровно один раз через каждую вершину графа. 3) Найдем хроматическое число и оптимальную раскраску вершин графа. Из Теоремы 4 о свойствах хроматического числа (стр. 39) следует: из п.1 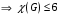 , так как граф имеет 6 вершин; , так как граф имеет 6 вершин; из п.4 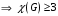 , так как граф , так как граф 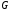 содержит полный подграф содержит полный подграф 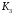 , имеющий три вершины , имеющий три вершины 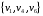 и и 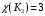 (п. 3 Теоремы 2); (п. 3 Теоремы 2); из п.7 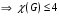 , так как граф , так как граф 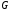 является планарным. является планарным.И так, из Теоремы 2 получаем: 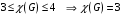 или или 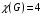 . .Пример оптимальной раскраски – используем три цвета: 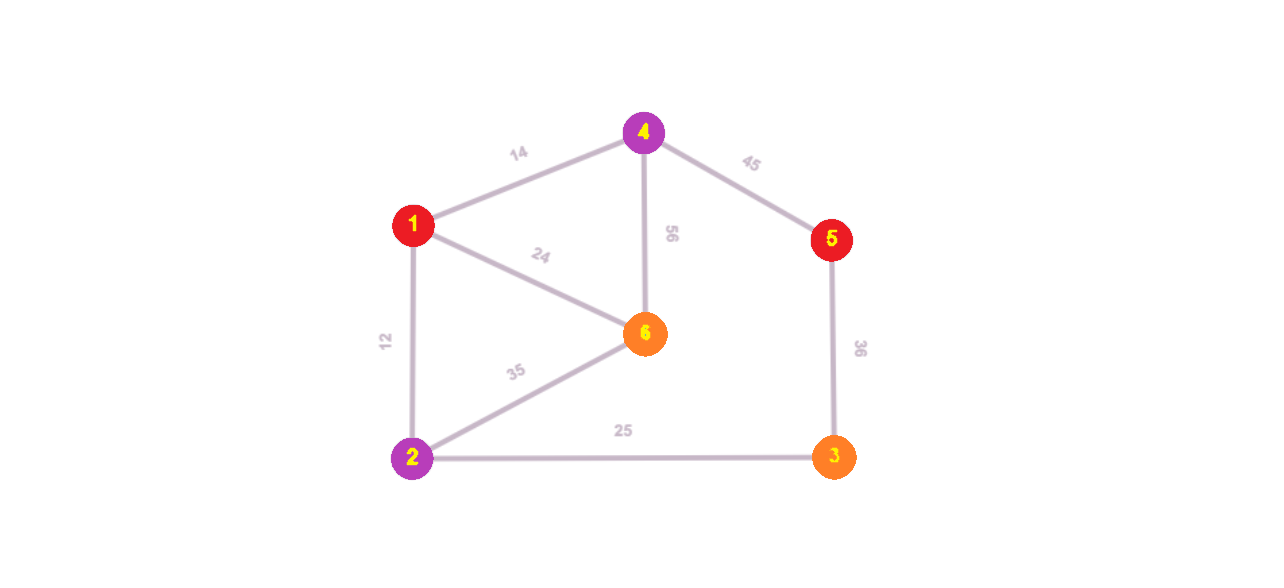 Следовательно, минимальное число цветов, достаточное для раскраски графа 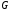 , - три - является его хроматическим числом: , - три - является его хроматическим числом: 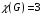 . .Москва, 2020 г. |
