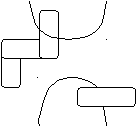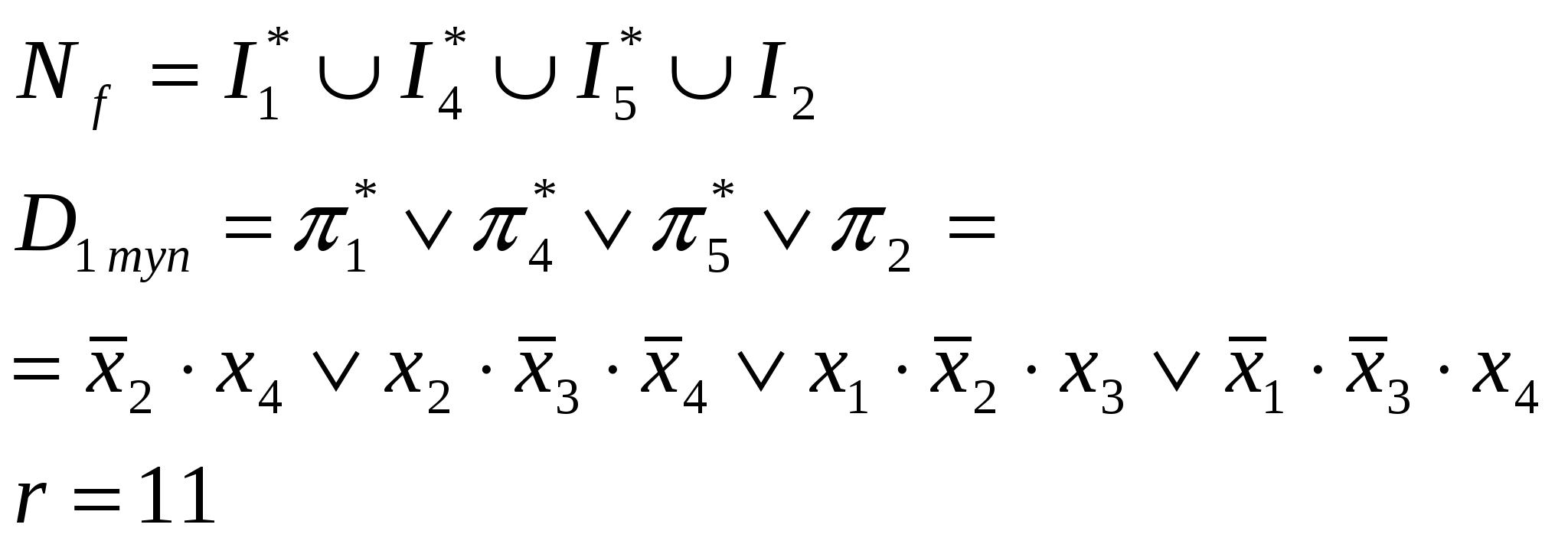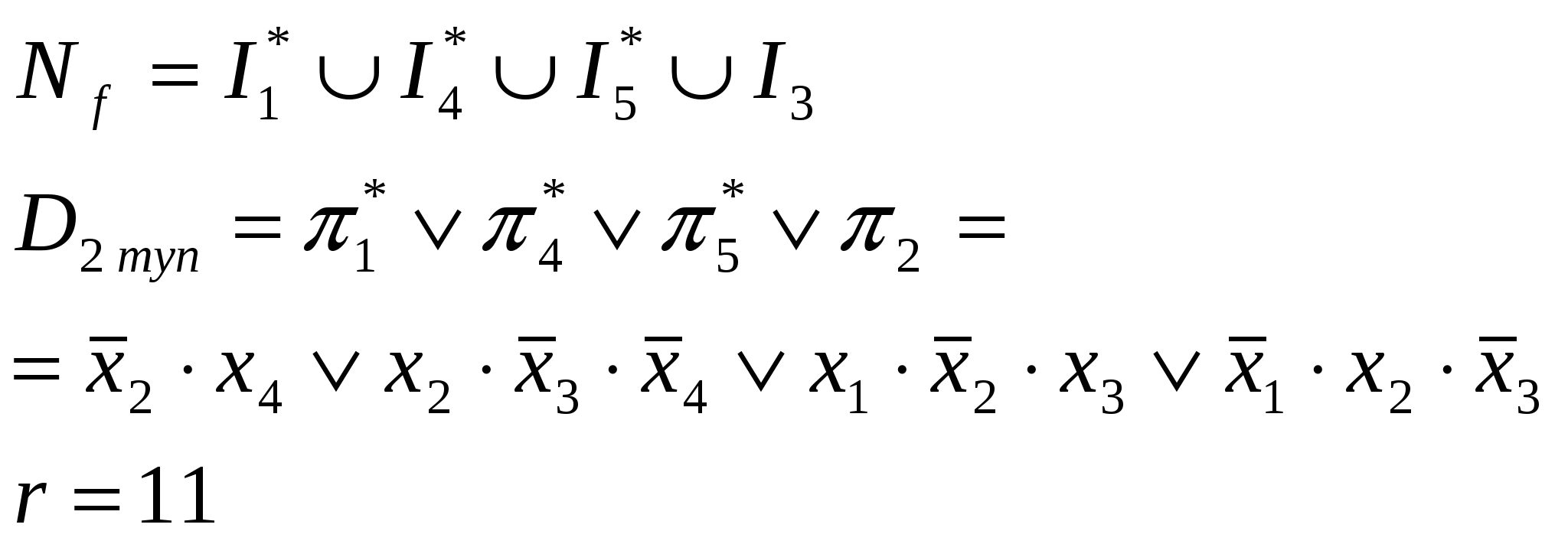Типовой расчёт. вар 63. Московский государственный институт радиотехники, электроники и автоматики
 Скачать 428.5 Kb. Скачать 428.5 Kb.
|
|
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ) Типовой расчёт по предмету « Основы дискретной математики » студента группы ВСС 1-97 Рахмукова Владимира Москва, 2000 г. Вариант 63 Задача 1 Проверить полноту системы функций ={ fi ; gj }, найти Dmin для функций fi , gj. Представить формулами над и функциональными схемами над функции 0,1,,&,,hk. 63 = (2100)3 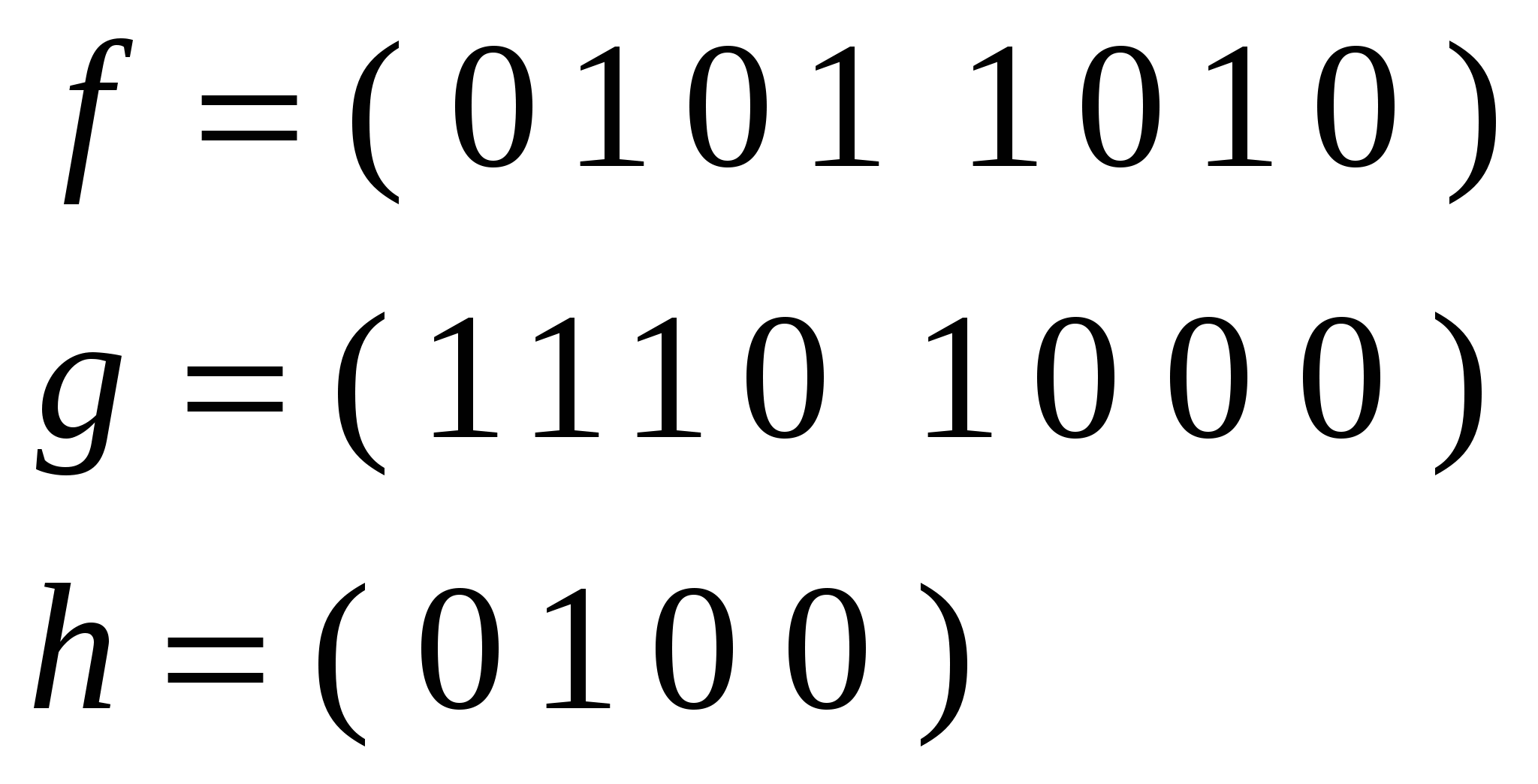
Определение линейности функции. Найдём многочлен Жегалкина для функций 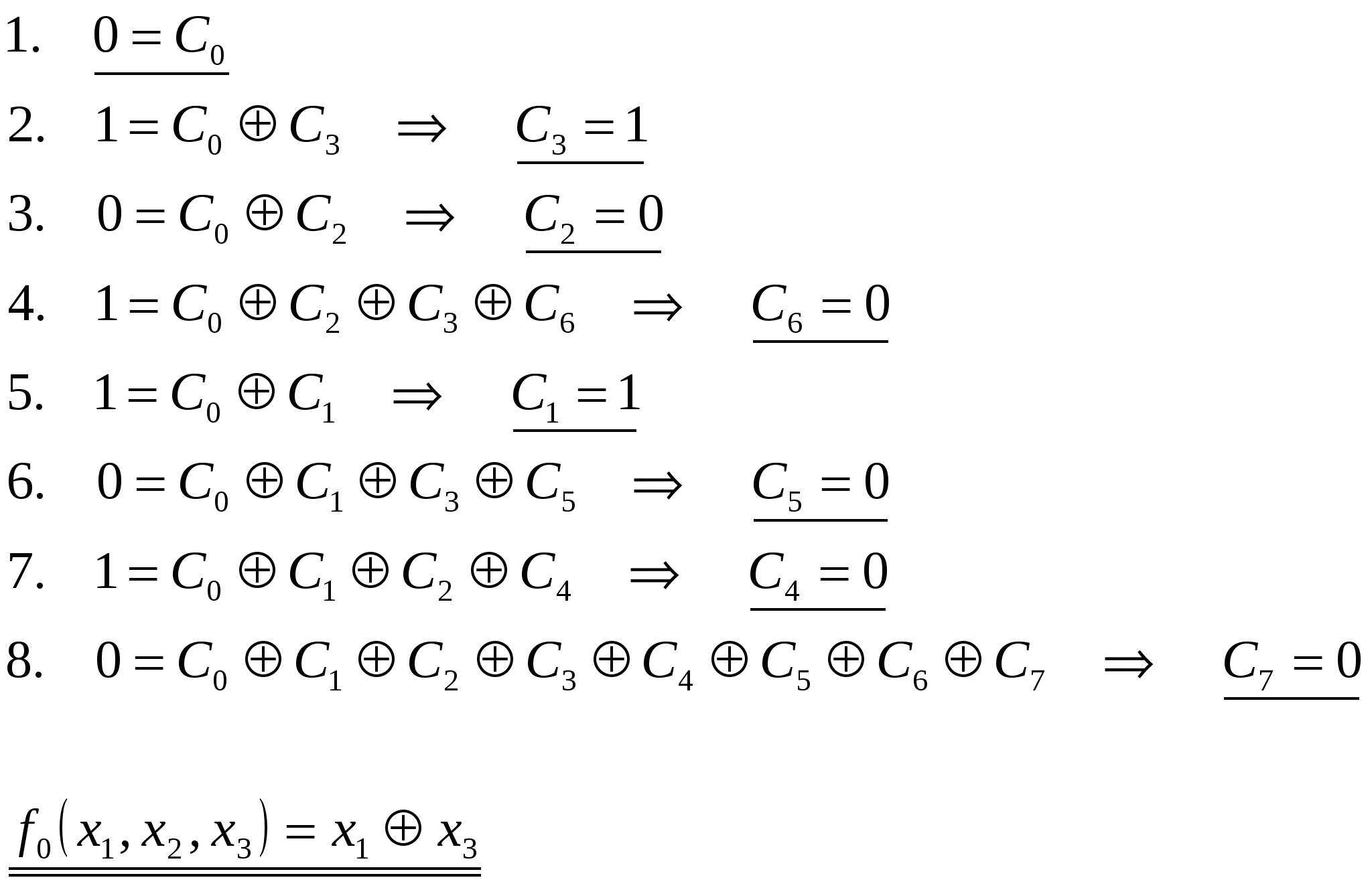 В многочлене Жегалкина конъюнкций переменных нет, следовательно, функция 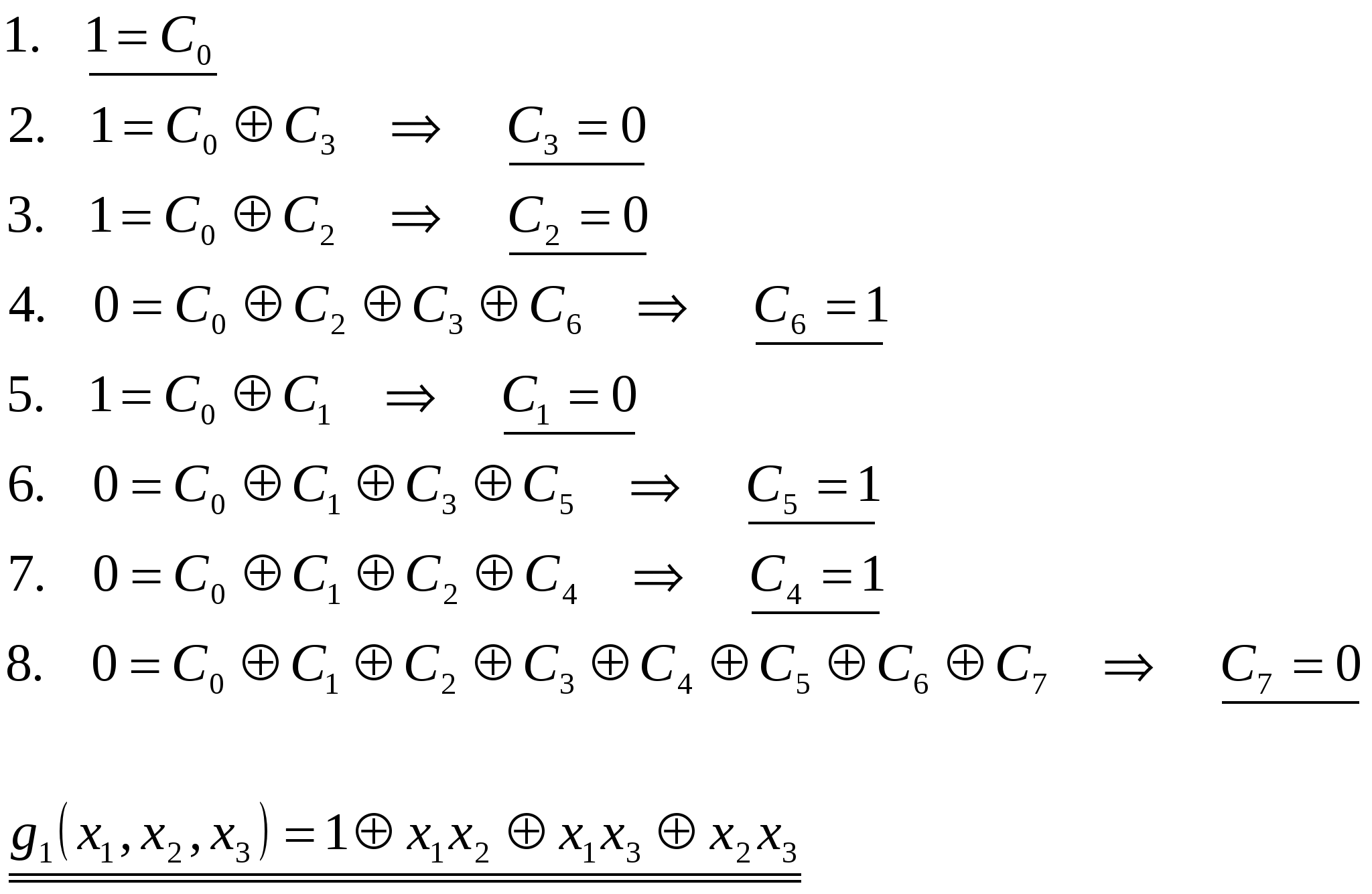 В многочлене Жегалкина есть конъюнкции переменных, поэтому функция Система функций
Доказательством достаточности является построение из функции системы
Воспользуемся Леммой 1, и из функции 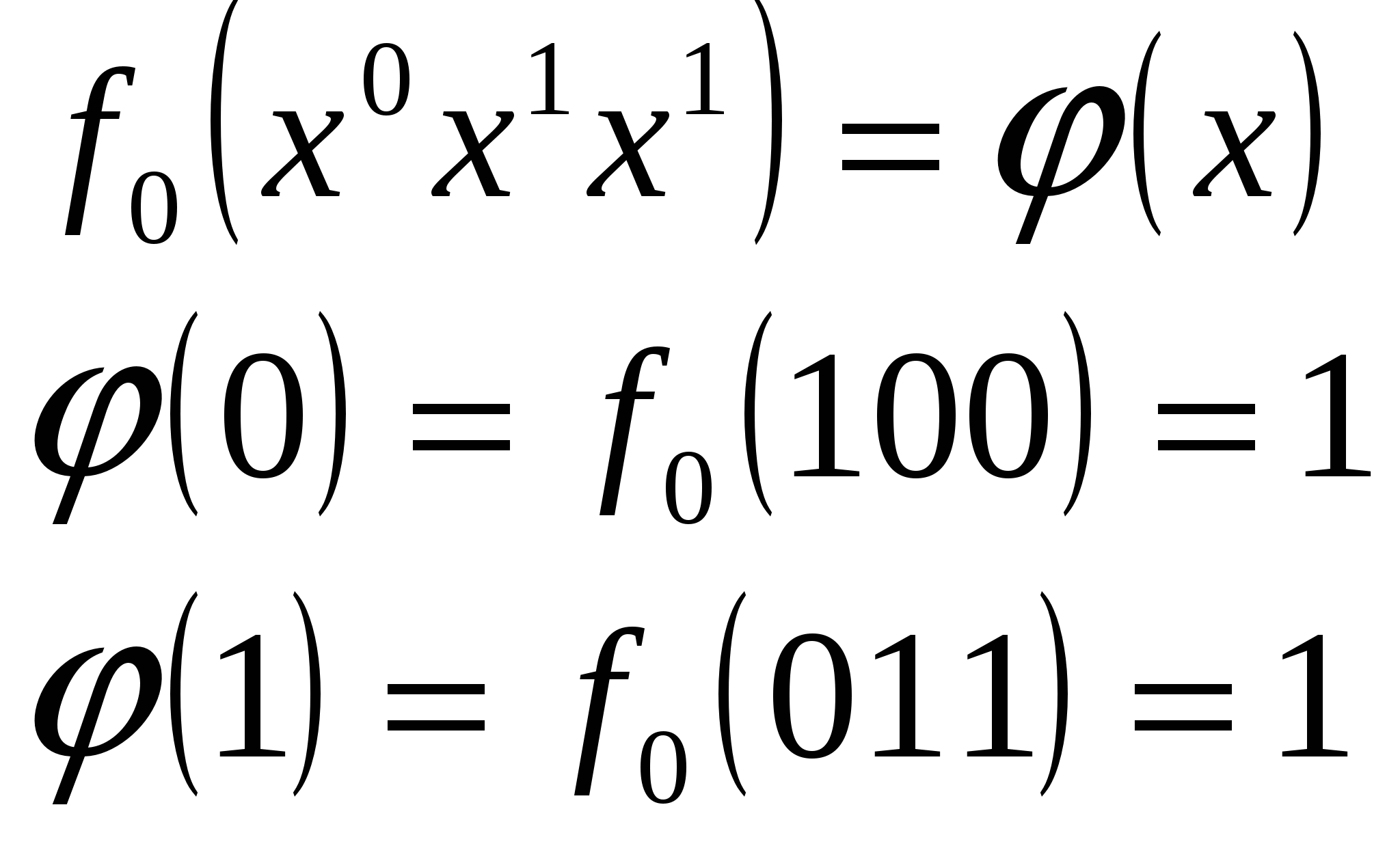 Взяв её отрицание, получим константу 0: 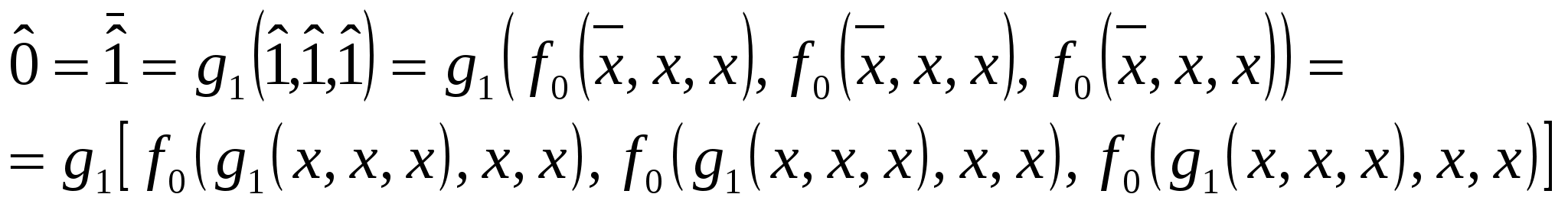 Константу 0 можно также получить и следующим образом: Берём 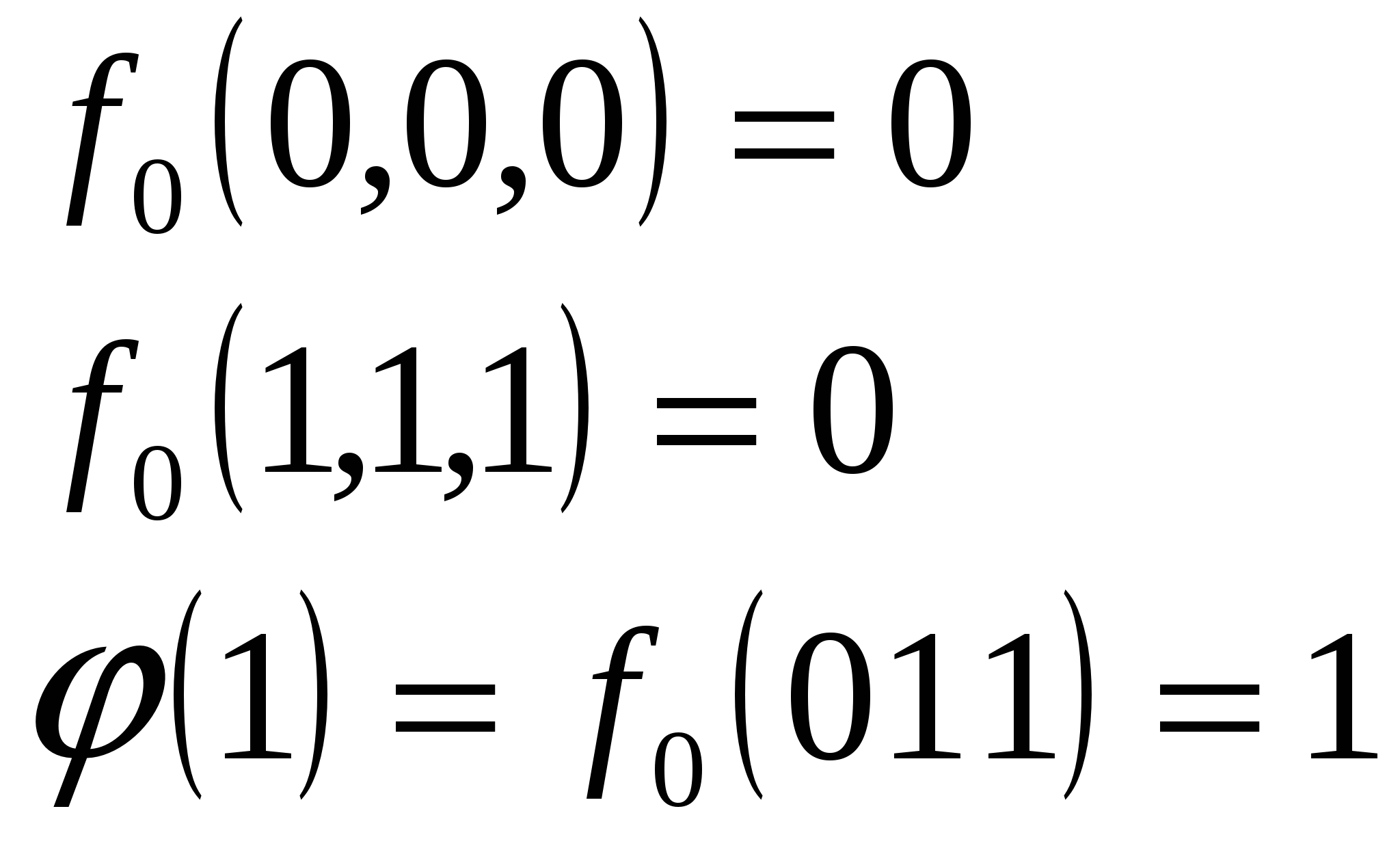 , следовательно , следовательно
Чтобы сохранить конъюнкцию 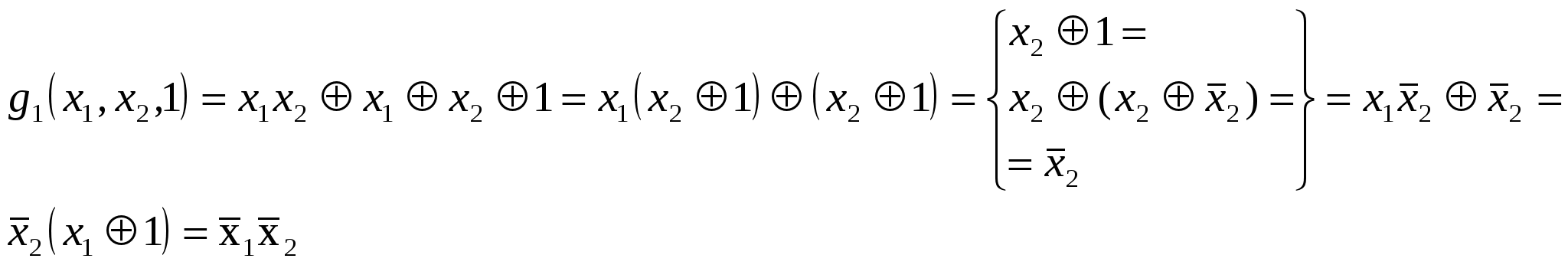 теперь вместо Дизъюнкцию xy получим по закону двойственности Формула над
Функциональные схемы над 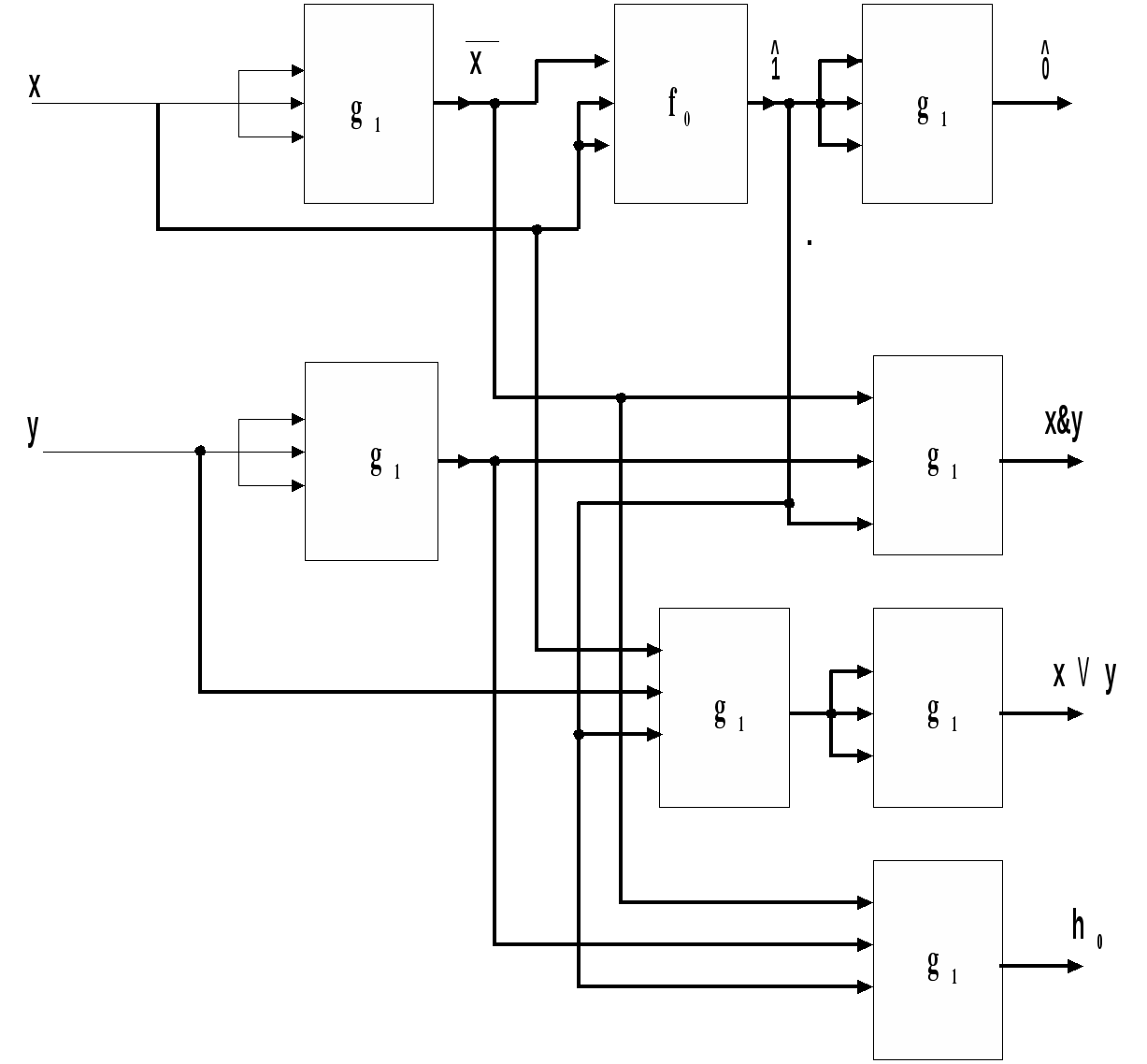 Определение Dмин для функций f0, g1 . 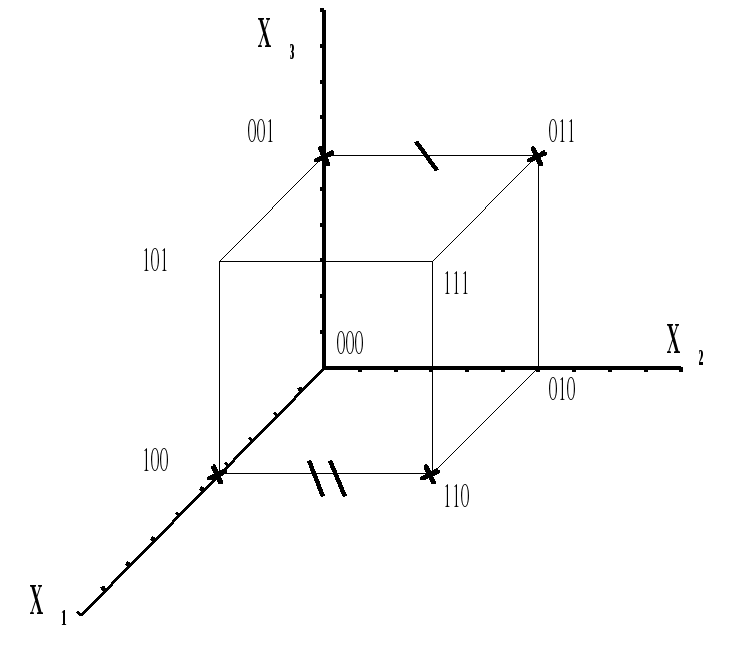
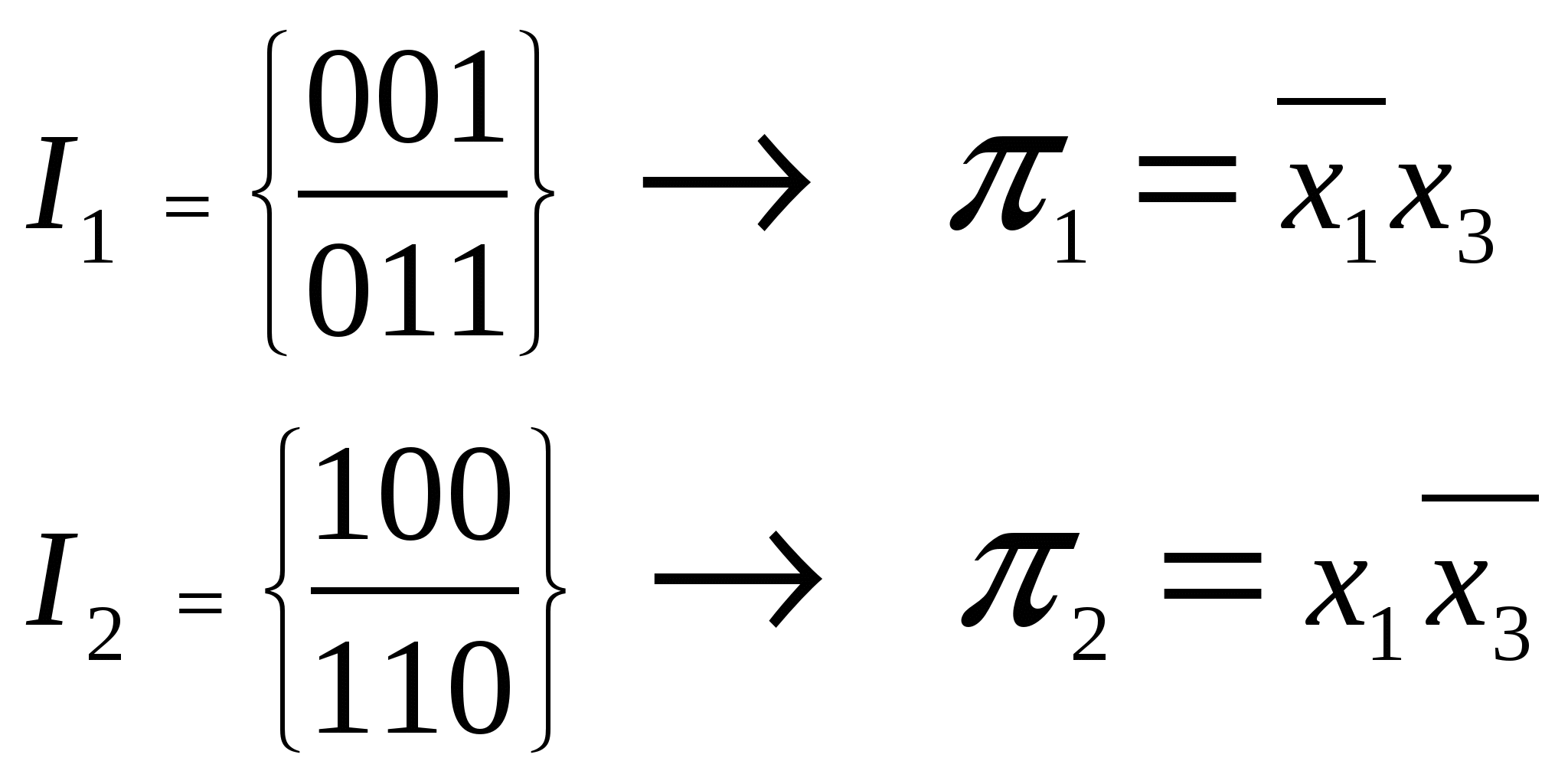
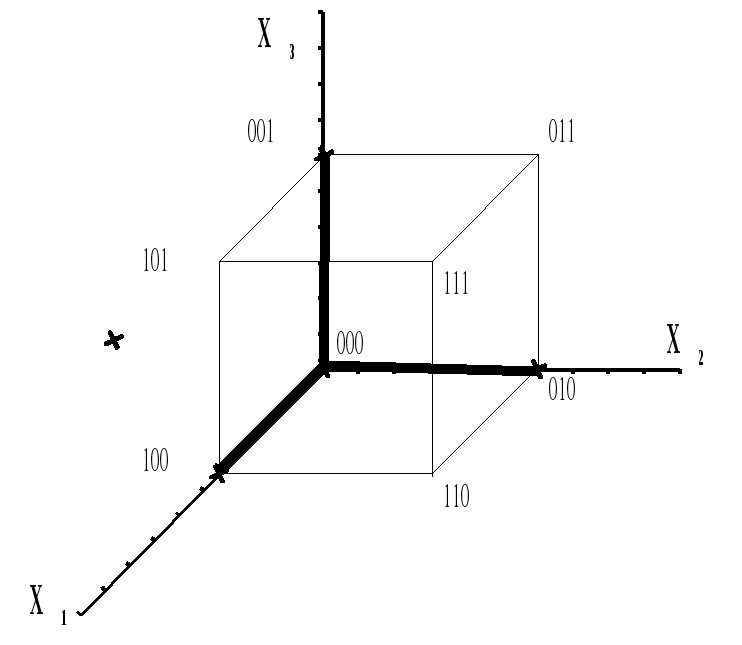
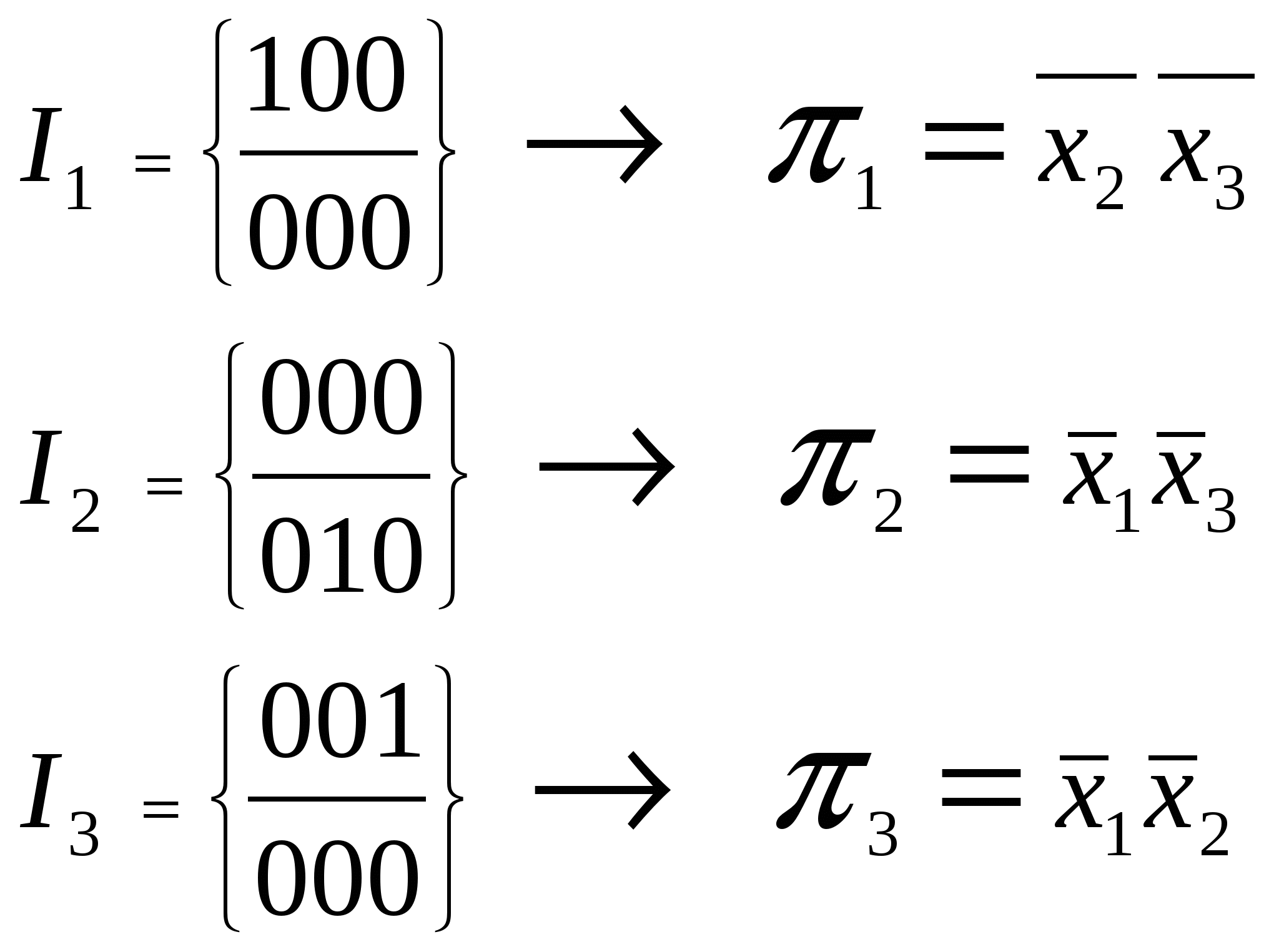
Задача 2 Найти Dсокр, Dя, все Dmin для f ( x1, x2, x3, x4 ) методом Карно и Квайна.  6 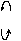 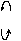 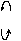 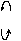 3= ( 0011 1111 )2 3= ( 0011 1111 )2 Метод Карно 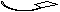
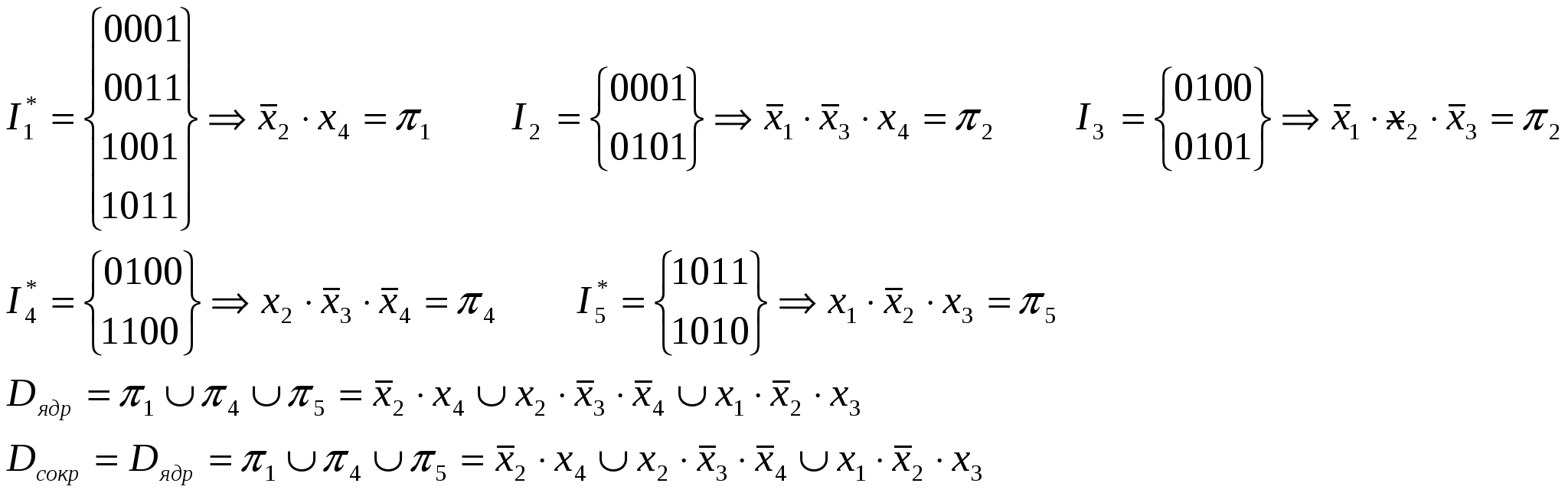
Dmin=D1туп=D2туп Метод Квайна.
      
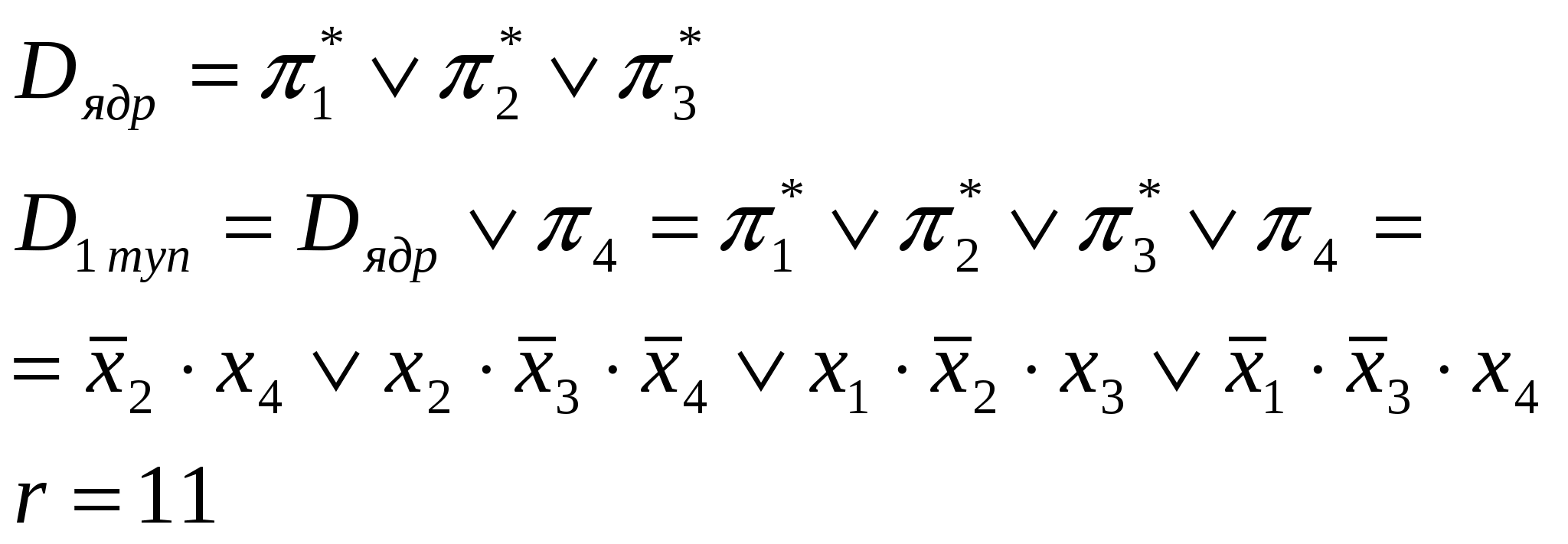 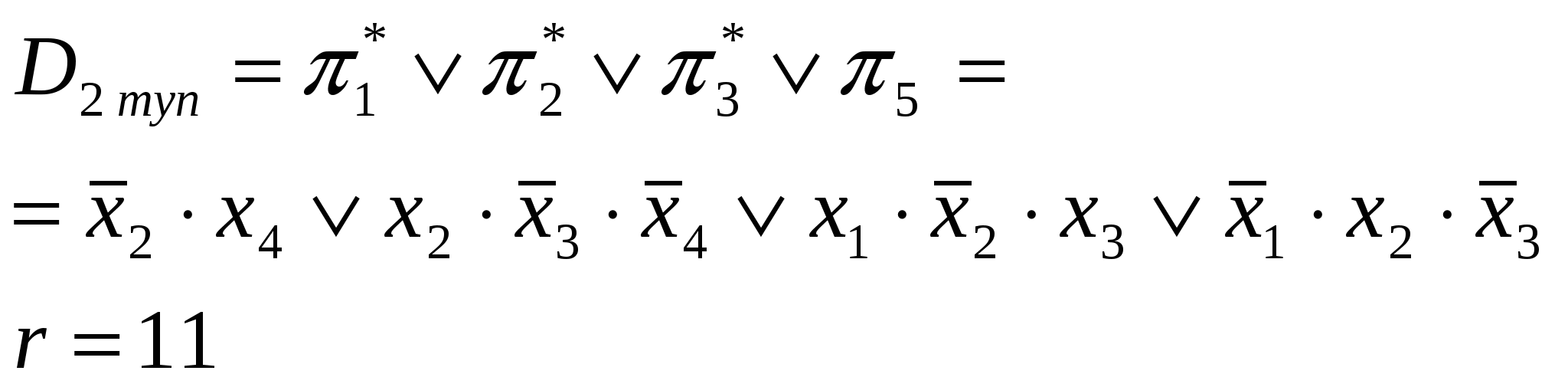 Dmin=D1=D2 Задача 3 Построить минимальную функциональную схему для функции f из задачи 2 на элементах {,&,}. 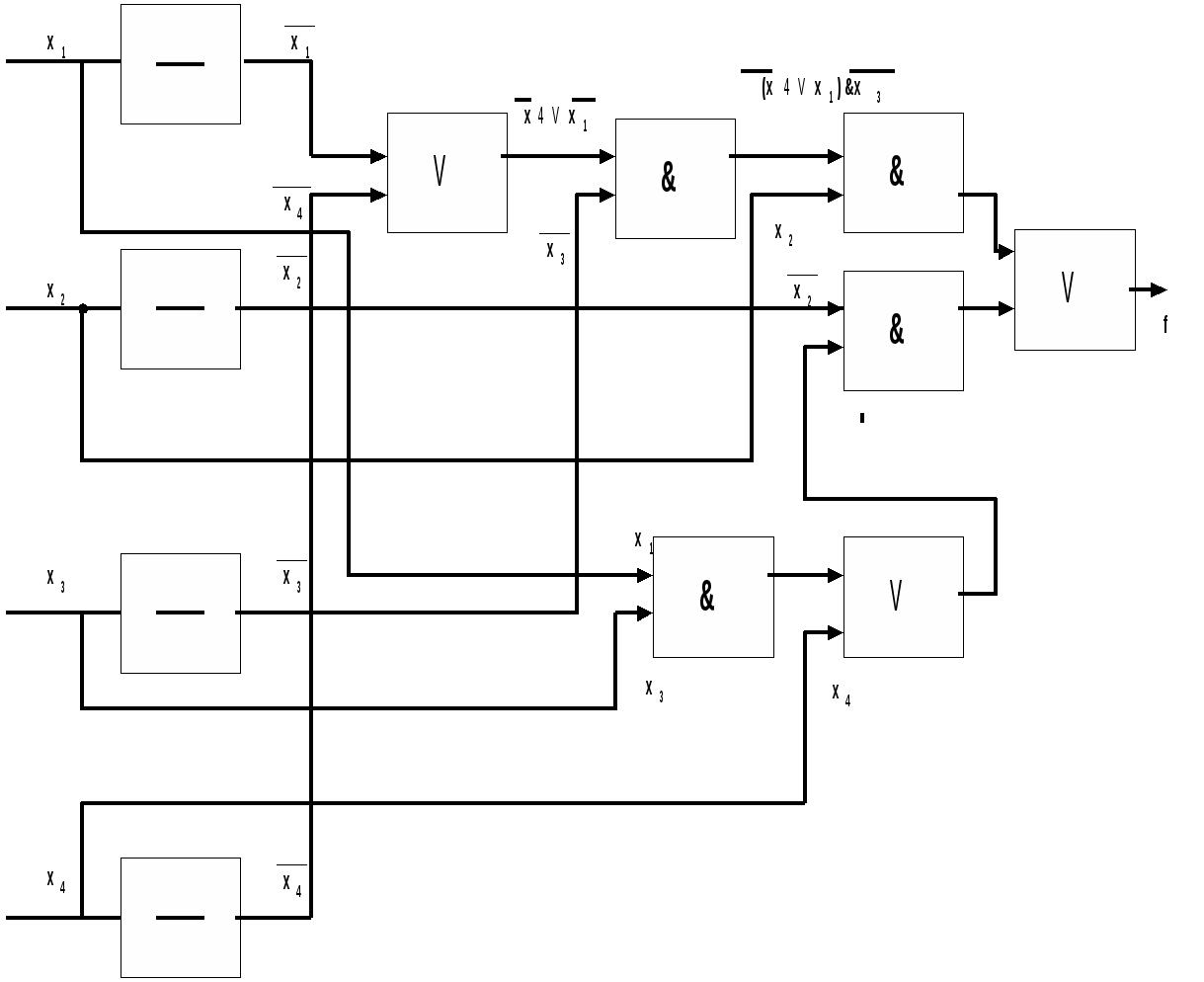 Задача 4 Построить минимальную контактную схему для той же функции. 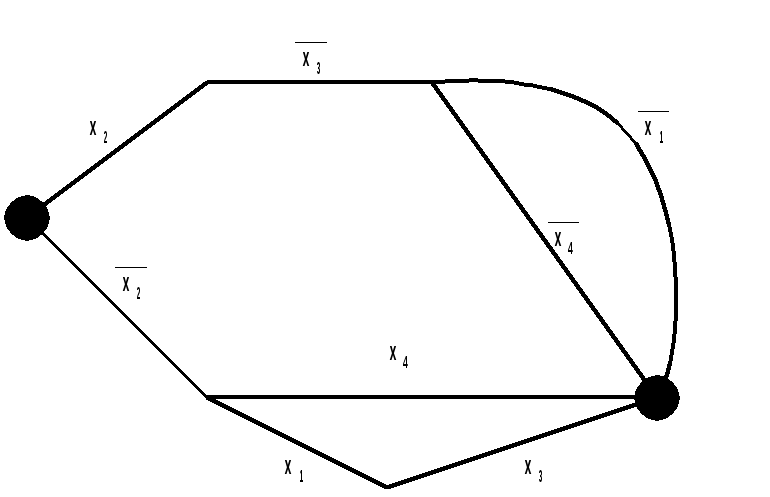 Задача 5 Решить задачу об оптимальном назначении с матрицей эффективности В. 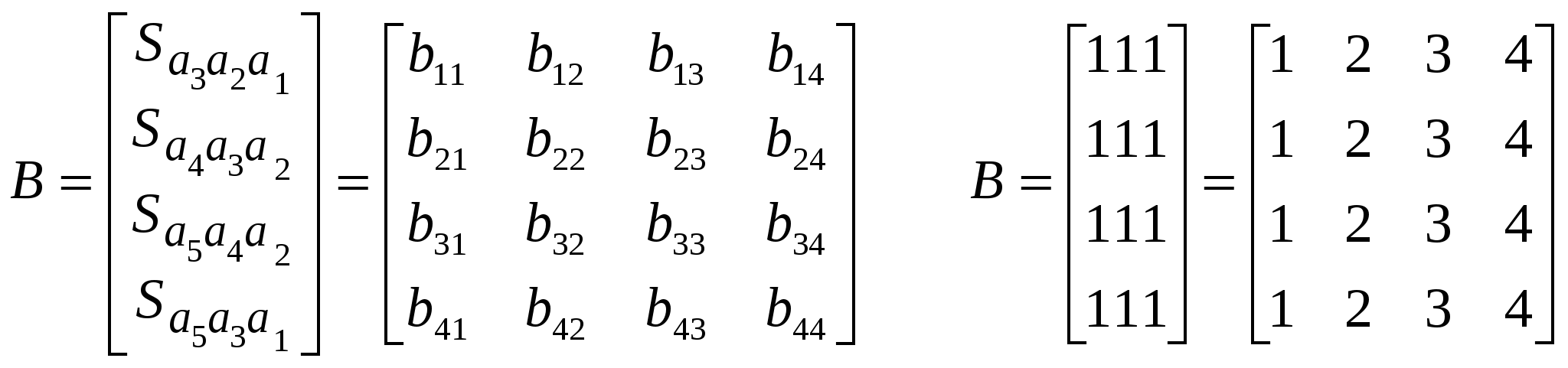 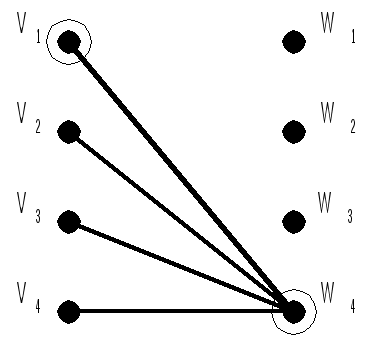
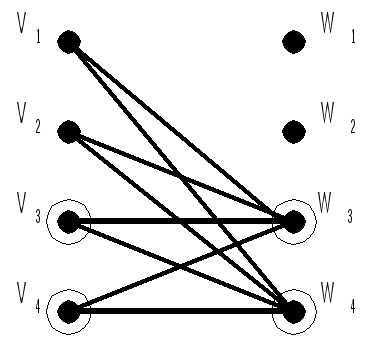
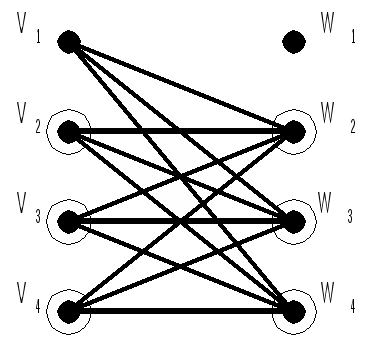
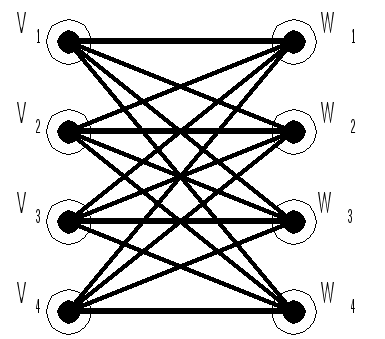
Задача 6 Найти максимальный поток в транспортной сети. Пропускная способность рёбер определяется элементами матрицы В из задачи 5. 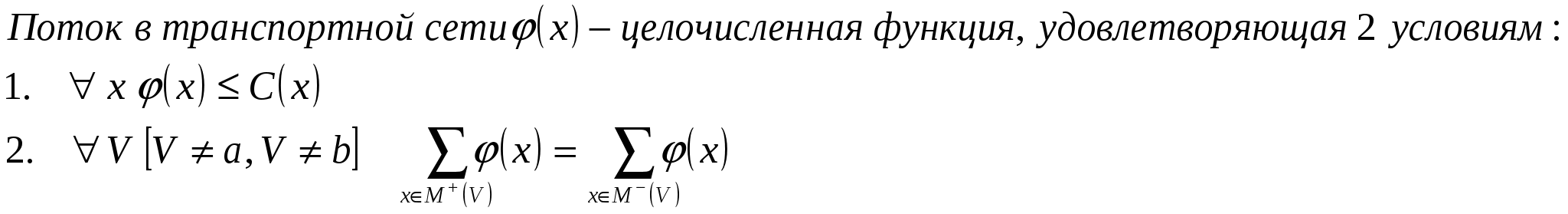                                 1 (1) 1 (1) 3 (1) 2 (0) 4 (0) 2 (0) 3 (0) 2 (2) 4 (2) 1 (0) 2 (0) 3 (3) 4 (3) 1 (0) 1 (0) b a G                 |  4 (3)  |