Лекция 4 Принцип получения гармонически изменяющегося тока
В основе получения промышленного гармонически (синусоидально) изменяющегося тока в замкнутой цепи лежит, известный из физики, закон электромагнитной индукции.
 где где
е(t) – ЭДС индукции, В – индукция магнитного поля,  - длина проводника, находящегося в магнитном поле, v – линейная скорость движения проводника в постоянном магнитном поле, - длина проводника, находящегося в магнитном поле, v – линейная скорость движения проводника в постоянном магнитном поле,  - скорость изменения магнитного потока. Знак «минус» связан с правилом Ленца. (смотри страницу 19) Если производная изменения магнитного потока по времени гармоническая функция, то возникнет гармонически изменяющаяся ЭДС, которая создаст гармонически изменяющийся ток в цепи. - скорость изменения магнитного потока. Знак «минус» связан с правилом Ленца. (смотри страницу 19) Если производная изменения магнитного потока по времени гармоническая функция, то возникнет гармонически изменяющаяся ЭДС, которая создаст гармонически изменяющийся ток в цепи.
Представление гармонических колебаний вращением вектора на комплексной плоскости
Математически это представляется следующим образом (рисунок 8). Для определённости рассмотрим изменение тока i, представленное на рисунке справа.
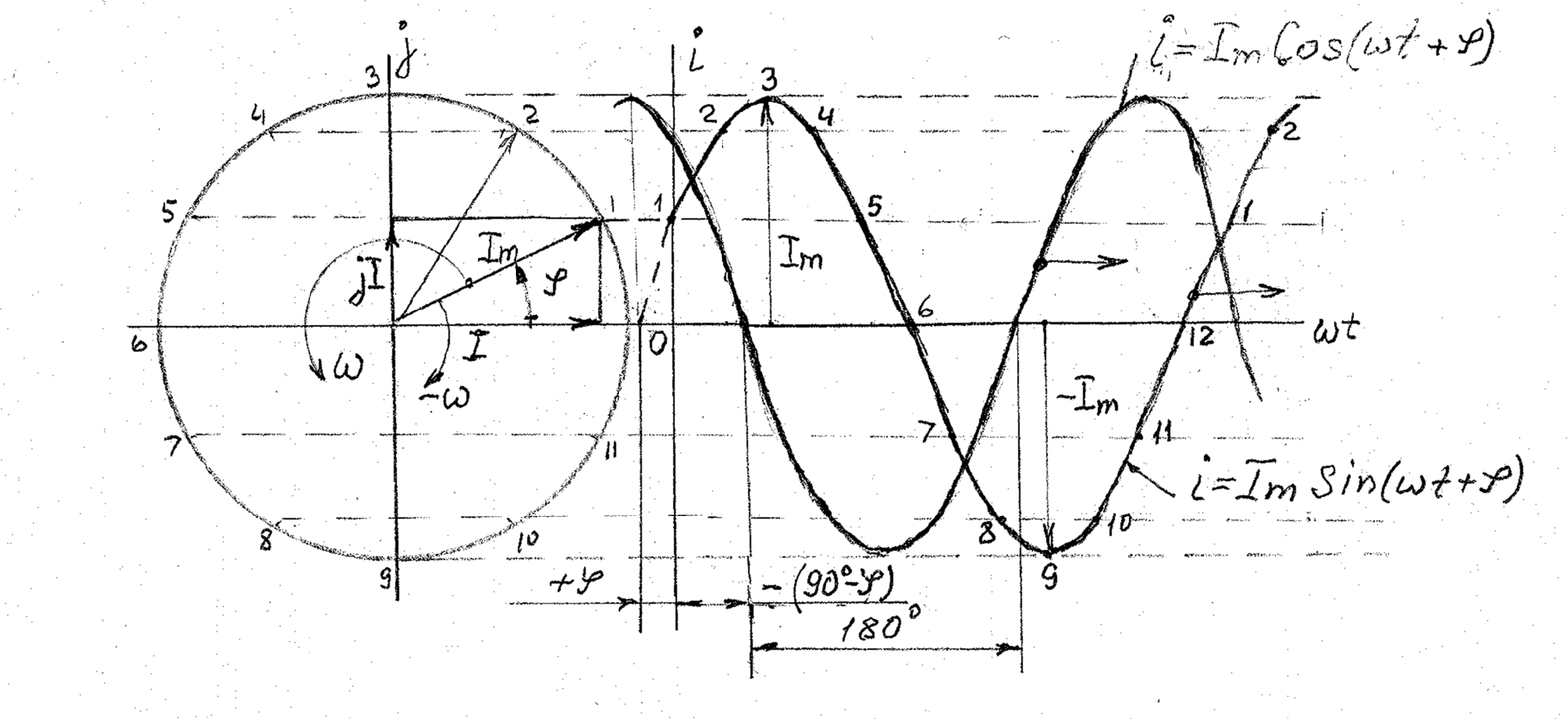
Рисунок 9. Представление гармонических колебаний вращением вектора на комплексной плоскости.
Сразу следует отметить особенность комплексной системы координат в электротехнике – ось мнимых значений обозначается буквой j, так как буква i уже занята током.
Вектор  начинает равномерно вращаться против часовой стрелки (это положительное направление вращения) из положения 1. В прямоугольной системе координат, где аргументом является выражение ωt в радианах, угловое положение вектора на комплексной плоскости. Последовательно перенося положение конца вектора начинает равномерно вращаться против часовой стрелки (это положительное направление вращения) из положения 1. В прямоугольной системе координат, где аргументом является выражение ωt в радианах, угловое положение вектора на комплексной плоскости. Последовательно перенося положение конца вектора  , в точки 1, 2, 3, и т.д. в прямоугольную систему координат ωt, i, получим гармонические колебания тока , в точки 1, 2, 3, и т.д. в прямоугольную систему координат ωt, i, получим гармонические колебания тока  , или , или  , где φ начальная фаза, то есть при t=0. Она определяет проекции вектора , где φ начальная фаза, то есть при t=0. Она определяет проекции вектора  на оси координат в комплексной системе, то есть при t=0 составляющие тока на оси координат в комплексной системе, то есть при t=0 составляющие тока  будут будут

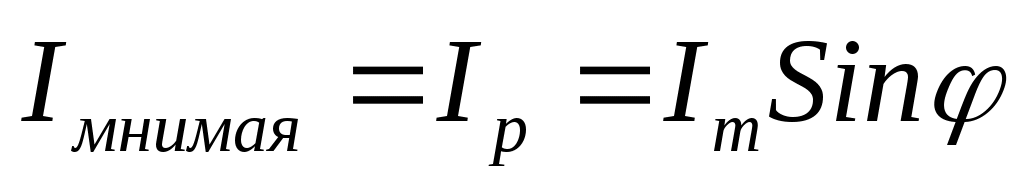
Или в векторной форме:  . Такая форма записи . Такая форма записи  называется алгебраической формой записи комплексного числа. Её удобно применять при сложении или вычитании векторов. называется алгебраической формой записи комплексного числа. Её удобно применять при сложении или вычитании векторов.
Вектор  , его положение на комплексной плоскости, можно определить, применив формулу Эйлера , его положение на комплексной плоскости, можно определить, применив формулу Эйлера
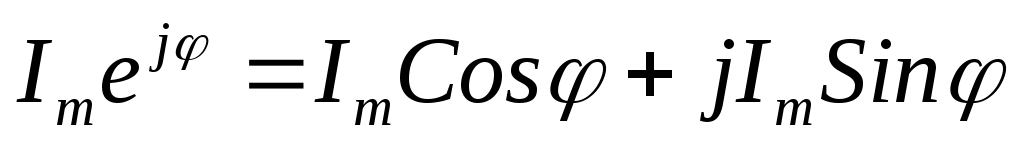
Выражение  называется показательной формой записи комплексного числа. Еёудобно применять при умножении и делении комплексных чисел называется показательной формой записи комплексного числа. Еёудобно применять при умножении и делении комплексных чисел
Переход от показательной формы записи к алгебраической очевиден – формула Эйлера. Обратный переход осуществляют, решая прямоугольный треугольник. Например, для вектора в позиции 8 (смотри рисунок 8, рекомендую сделать необходимую часть рисунка самостоятельно). По теореме Пифагора очень легко найти его длину  . Начальную фазу удобно отсчитать по часовой стрелке от оси действительных значений, то есть она будет больше 900 и отрицательная. Таким образом, решая прямоугольный треугольник . Начальную фазу удобно отсчитать по часовой стрелке от оси действительных значений, то есть она будет больше 900 и отрицательная. Таким образом, решая прямоугольный треугольник

Обратите внимание на тот факт, что знаки действительной и мнимой частей не учитываются, так как решается треугольник вне комплексной плоскости.
Опережение и отставание гармонических колебаний
В электротехнике необходимо знать какое гармоническое колебание впереди по сравнению с другими. Этим определяется характер электрической цепи, чего больше индуктивности или ёмкости.тар
Внимательно посмотрите на рисунок 8. Колебания распространяются вправо. Определить какая кривая впереди можно только, взглянув на начало координат. При t=0 косинус имеет максимальное значение, следовательно, он начал раньше синуса, то есть косинус опережает синус на 90 градусов. Обратите внимание на знаки начальных фаз. Фаза φ слева от нуля, но она положительна. Начальная фаза для косинуса справа от нуля [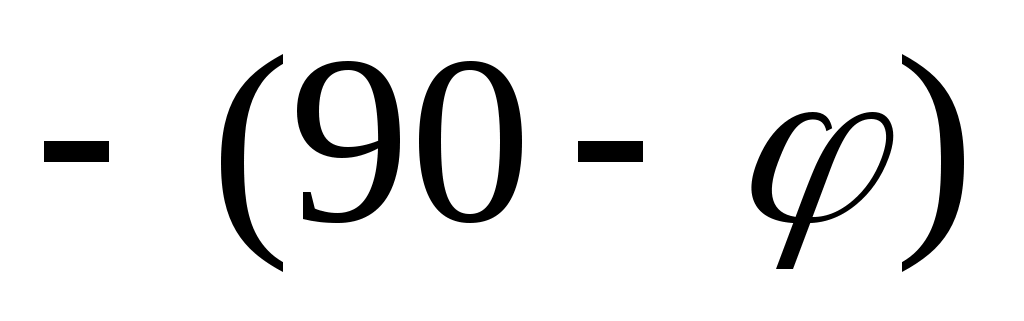 ] отрицательная. (или в другую сторону - положительная 90+φ). Сопоставьте это с направлением вращения вектора и направлением отсчета начальной фазы всегда от оси действительных значений. ] отрицательная. (или в другую сторону - положительная 90+φ). Сопоставьте это с направлением вращения вектора и направлением отсчета начальной фазы всегда от оси действительных значений.
Понятие комплексных амплитуд
Рассмотрим показательную форму записи комплексного числа для вращающегося вектора, когда получаются гармонические колебания

Сомножитель  является циклической составляющей, говорящей о вращении вектора. Сомножитель является циклической составляющей, говорящей о вращении вектора. Сомножитель  - остановленный вектор в положении начальной фазы. Эта векторная величина используется при расчете цепей переменного тока. Она получила название комплексная амплитуда и обозначается с точкой наверху. - остановленный вектор в положении начальной фазы. Эта векторная величина используется при расчете цепей переменного тока. Она получила название комплексная амплитуда и обозначается с точкой наверху.
 = =
Точка показывает, что это векторная величина на комплексной плоскости.
Переменная ЭДС  создаёт в цепи гармонически меняющийся ток, поэтому расчет можно вести только для какого-то конкретного значения времени t.Это конкретное время задаётся начальной фазой ЭДС, то есть вместо вращающегося вектора имеем остановленный, заданный для расчета значением комплексной амплитуды или комплексным действующим значением Ė=Е создаёт в цепи гармонически меняющийся ток, поэтому расчет можно вести только для какого-то конкретного значения времени t.Это конкретное время задаётся начальной фазой ЭДС, то есть вместо вращающегося вектора имеем остановленный, заданный для расчета значением комплексной амплитуды или комплексным действующим значением Ė=Е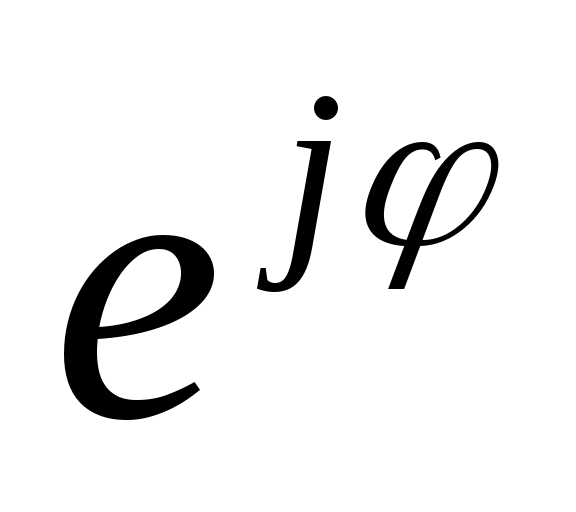 . .
Индуктивность и ёмкость в цепи переменного тока
Вспомним явление самоиндукции. ЭДС самоиндукции пропорциональна скорости изменения магнитного потока, созданным электрическим током в самой катушке индуктивности.

Магнитный поток создан движущимися электрическими зарядами, то есть током. Изменяется ток, изменяется магнитный поток, полностью повторяя изменение тока, создавая ЭДС самоиндукции, ток от которой будет иметь такое направление, чтобы своим магнитным полем препятствовать изменению магнитного поля в катушке, то есть навстречу току в катушке, (правило Ленца). С точки зрения электрических мощностей ЭДС самоиндукции является потребителем электрической энергии (её направление не совпадает с направлением электрического тока в катушке). Она создаёт препятствие (сопротивление) току. Это сопротивление получило название «индуктивное сопротивление», и обозначается оно  . Нетрудно заметить, что ЭДС самоиндукции будет возрастать с увеличением частоты ω, так как при этом возрастает скорость изменения магнитного потока. . Нетрудно заметить, что ЭДС самоиндукции будет возрастать с увеличением частоты ω, так как при этом возрастает скорость изменения магнитного потока.
Напряжение на индуктивности равно по модулю ЭДС самоиндукции, но имеют противоположное направление. Считая, что ток в индуктивности  , для напряжения на индуктивности получим , для напряжения на индуктивности получим

Круглые скобки в этом выражении имеют логическое значение, подчеркивая, что это сопротивление в законе Ома, следовательно

Следует также отметить, что ток в индуктивности изменяется по закону синуса, а напряжение на индуктивности – по закону косинуса, то есть  опережает опережает  на 900. Такое опережение могло внести только сопротивление на 900. Такое опережение могло внести только сопротивление  , следовательно, это сопротивление имеет положительную начальную фазу равную 900, и в векторной записи , следовательно, это сопротивление имеет положительную начальную фазу равную 900, и в векторной записи
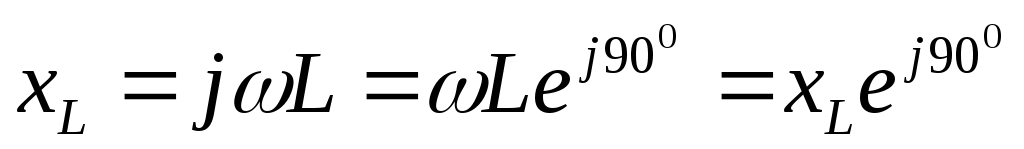
Точку над комплексными значениями сопротивлений и проводимостей не ставят, понятно и так, когда это вектор, а когда модуль вектора.
Ёмкость во всём противоположна индуктивности. Рассуждая аналогично, получим:
 
То есть на ёмкости напряжение  отстаёт от тока отстаёт от тока  на 900. Опираясь на закон Ома, выражение на 900. Опираясь на закон Ома, выражение 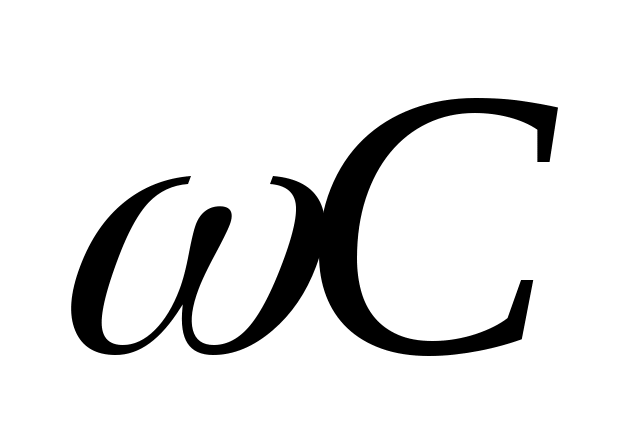 является проводимостью ёмкости, и, соответственно, является проводимостью ёмкости, и, соответственно,

Напомним, что в электротехнике фаза отсчитывается всегда от тока и положительное направление вращения против часовой стрелки, тогда в векторной форме

Закон Ома для цепей переменного тока
Для цепей переменного тока применяют закон Ома в комплексной форме:
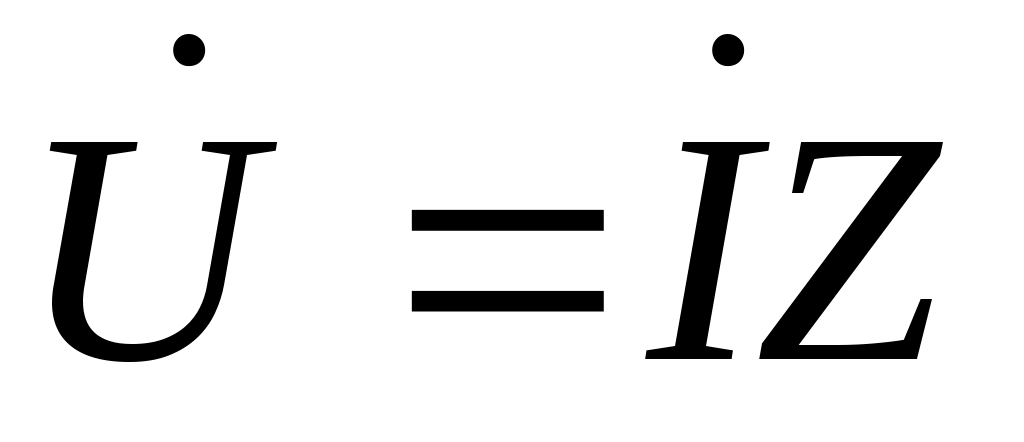 , ,
Где  , комплексное сопротивление. «Минус», если преобладает ёмкостное сопротивление, оно имеет фазу «минус 90 градусов». «+jx», если в сопротивлении Z преобладает индуктивность. Комплексное сопротивление это вектор на комплексной плоскости. Точка над Z не ставится. Начертание заглавной буквы Z без чёрточки посредине говорит, что это вектор. Модуль комплексного сопротивления обозначается малой буквой z. (малая «зет» с черточкой посередине) , комплексное сопротивление. «Минус», если преобладает ёмкостное сопротивление, оно имеет фазу «минус 90 градусов». «+jx», если в сопротивлении Z преобладает индуктивность. Комплексное сопротивление это вектор на комплексной плоскости. Точка над Z не ставится. Начертание заглавной буквы Z без чёрточки посредине говорит, что это вектор. Модуль комплексного сопротивления обозначается малой буквой z. (малая «зет» с черточкой посередине)
Рассмотрим схему простой электрической цепи.
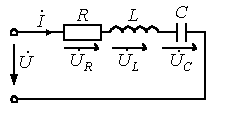
Рисунок 10. Электрическая цепь переменного тока
Приложенное к цепи напряжение:  . Здесь . Здесь  , ,  Ом. Um=100 Bольт. В комплексной форме записи Ом. Um=100 Bольт. В комплексной форме записи  . Коэффициент . Коэффициент  необходим для перехода от заданного амплитудного значения 100 В к действующему значению. Определим реактивные сопротивления, если L=0,1 Гн, а С=65 мкф необходим для перехода от заданного амплитудного значения 100 В к действующему значению. Определим реактивные сопротивления, если L=0,1 Гн, а С=65 мкф
 Ом Ом  Ом Это найдены модули сопротивлений. Их комплексные значения: Ом Это найдены модули сопротивлений. Их комплексные значения:
 Ом Ом
 Ом Ом
Таким образом, у нас есть все данные в комплексной форме записи для определения тока в цепи.
По второму закону Кирхгофа:
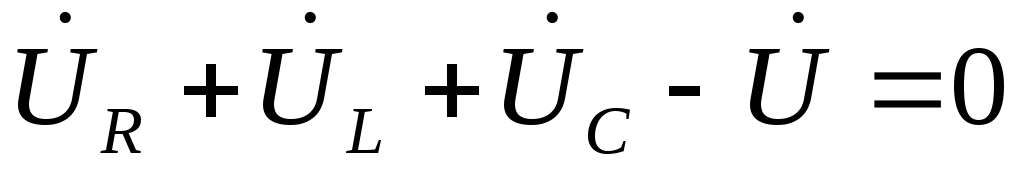
Раскрыв все значения напряжений по закону Ома
 или или

Где  - полное сопротивление цепи, записанное в комплексной (векторной) форме - полное сопротивление цепи, записанное в комплексной (векторной) форме
Или в числах
 (А) (А)
Переход от алгебраической формы 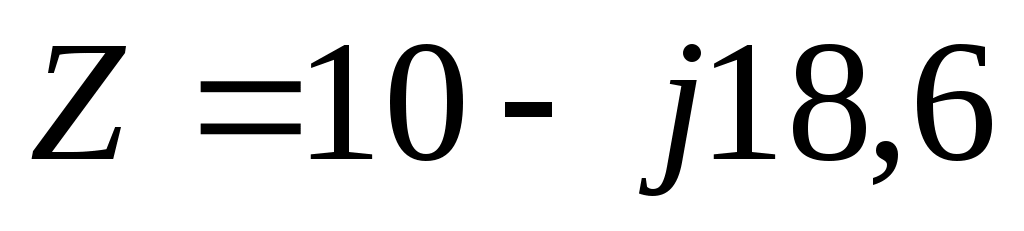 к показательной для производства деления был рассмотрен в разделе «Представление гармонических колебаний вращением вектора на комплексной плоскости» к показательной для производства деления был рассмотрен в разделе «Представление гармонических колебаний вращением вектора на комплексной плоскости»
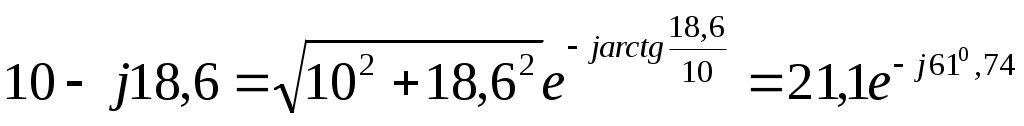 , ,
так как вектор (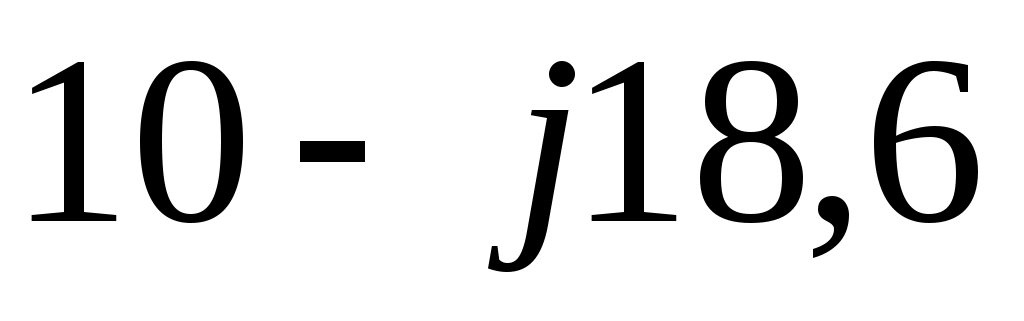 ), заданный проекциями на оси комплексной системы координат находится в четвёртой четверти и прилегает к оси мнимых значений (рисунок сделайте сами). Полученный результат является промежуточным. Для завершения расчета нужно найти мгновенное значение полученного тока как функцию времени. ), заданный проекциями на оси комплексной системы координат находится в четвёртой четверти и прилегает к оси мнимых значений (рисунок сделайте сами). Полученный результат является промежуточным. Для завершения расчета нужно найти мгновенное значение полученного тока как функцию времени.
Обратите внимание на тот факт, что при расчете мы пользовались значением 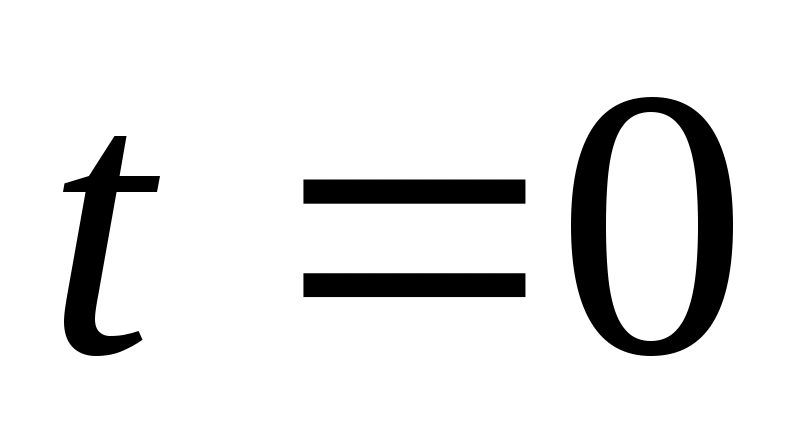 для приложенного напряжения для приложенного напряжения  , но с синусом, как видно из рисунка 8, связана мнимая составляющая приложенного напряжения, а работает составляющая, связанная с косинусом. Поэтому общее правило перехода к мгновенному значению: , но с синусом, как видно из рисунка 8, связана мнимая составляющая приложенного напряжения, а работает составляющая, связанная с косинусом. Поэтому общее правило перехода к мгновенному значению:
 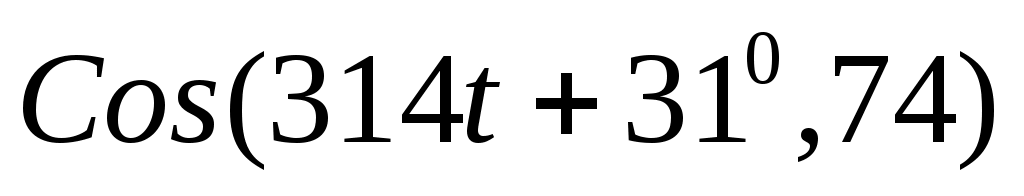
Но в нашем случае приложенное напряжение было задано именно мнимой частью, поэтому у нас   . Коэффициент . Коэффициент  - обратный переход от действующего значения (по которому велся расчет) к амплитудному. - обратный переход от действующего значения (по которому велся расчет) к амплитудному.
Ещё одно замечание. Полученный результат 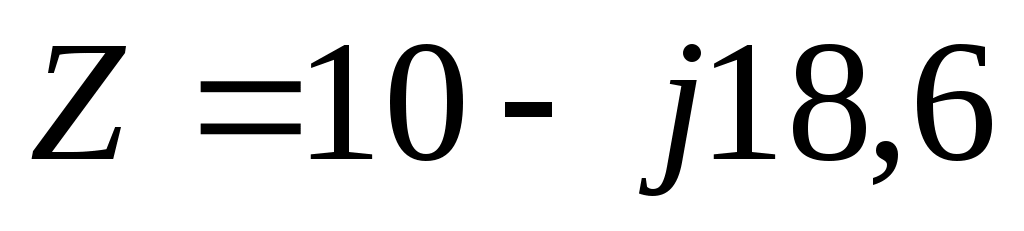 имеет отрицательную мнимую часть, как и имеет отрицательную мнимую часть, как и 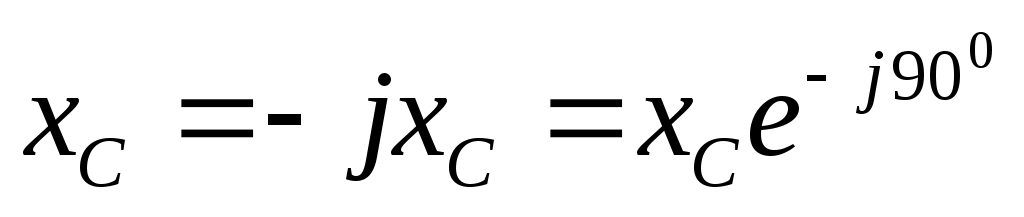 , то есть Z имеет ёмкостной характер, цепь в целом ёмкостная, а для ёмкости характерно отставание напряжения от тока. На самой ёмкости это 90 градусов, а по отношению к входному напряжению: , то есть Z имеет ёмкостной характер, цепь в целом ёмкостная, а для ёмкости характерно отставание напряжения от тока. На самой ёмкости это 90 градусов, а по отношению к входному напряжению:

Рисунок 11. Векторная диаграмма электрической цепи с ёмкостным характером
Сдвиг между током и напряжением по фазе произошёл из-за наличия в полном сопротивлении Z реактивной составляющей. Если бы не было ( ), ток и напряжение совпали по фазе (-300). Начальная фаза Z «минус 61 градус и 74 сотых градуса». Чтобы получить «минус» (смотри рисунок 9) нужно угол отсчитывать по часовой стрелке, то есть от тока. Фазовые углы всегда отсчитываются от направления тока. ), ток и напряжение совпали по фазе (-300). Начальная фаза Z «минус 61 градус и 74 сотых градуса». Чтобы получить «минус» (смотри рисунок 9) нужно угол отсчитывать по часовой стрелке, то есть от тока. Фазовые углы всегда отсчитываются от направления тока.
Векторная диаграмма напряжений
Векторная диаграмма напряжений – это графическое подтверждение выполнения второго закона Кирхгофа «Векторная сумма напряжений в контуре равна нулю».
Вернёмся к рисунку 8
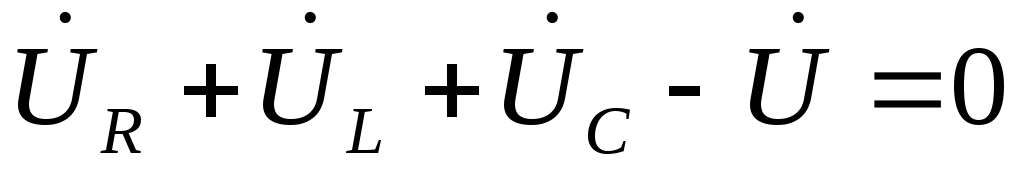
 = = 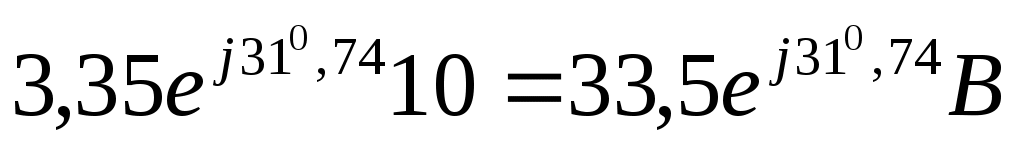
 = = 
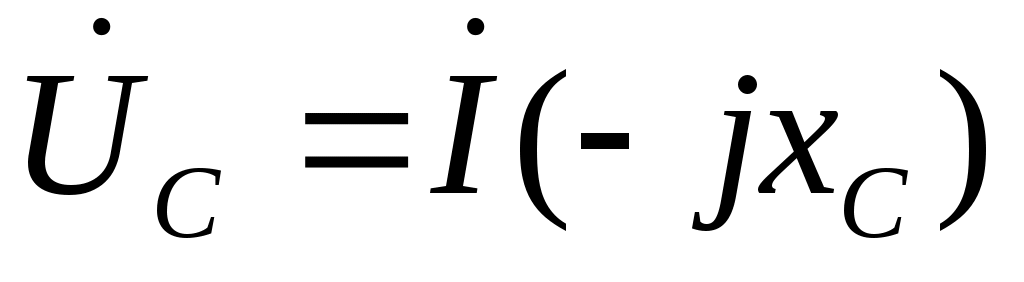 = = 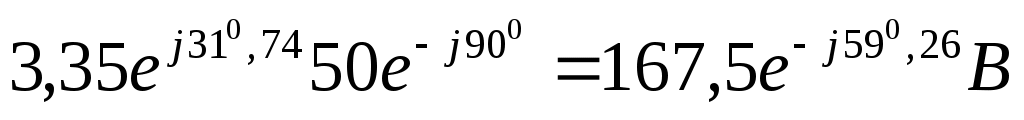


Рисунок 12. Векторная диаграмма напряжений
Здесь для сложения векторов применено правило: конец предыдущего, начало следующего. На рисунке применены более правильные индексы напряжений. Например , напряжение 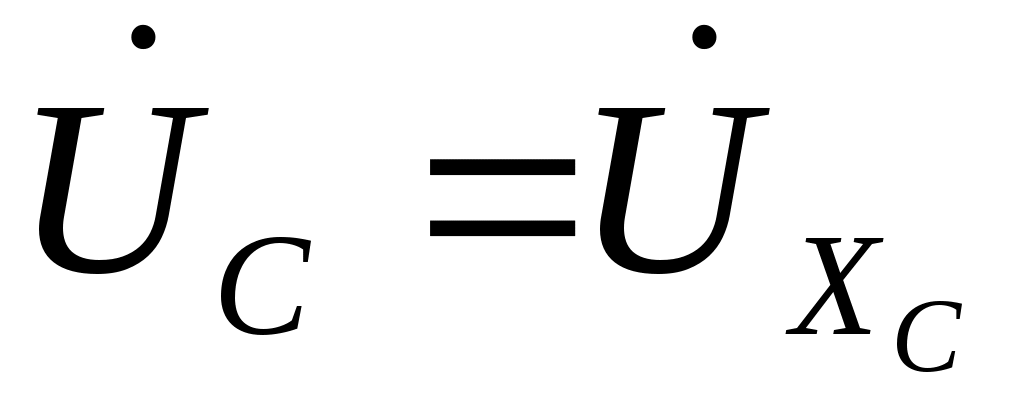 , то есть напряжение на сопротивлении , то есть напряжение на сопротивлении 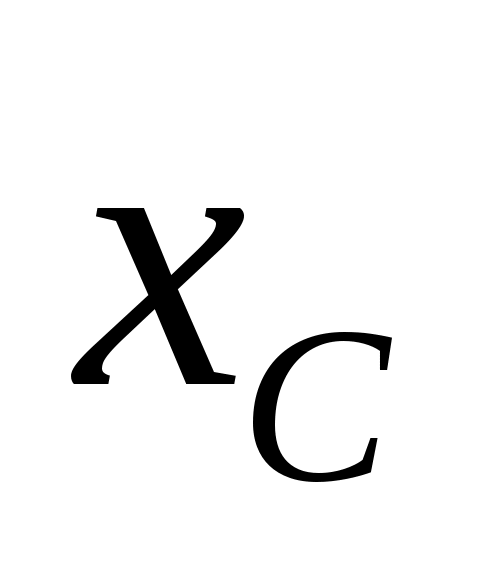 . Последний вектор . Последний вектор 
должен быть прибавлен с противоположным знаком, то есть стрелка 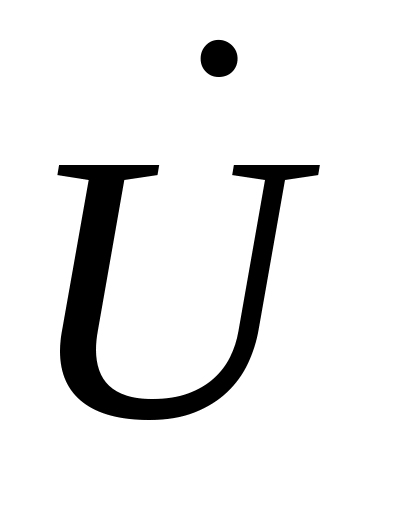 должна быть направлена к центру системы координат. На рисунке 10 векторная диаграмма соответствует уравнению должна быть направлена к центру системы координат. На рисунке 10 векторная диаграмма соответствует уравнению

Здесь векторная диаграмма построена с соблюдением масштаба и следующих правил:
Напряжение на активном сопротивлении, т.е. R совпадает по направлению с током;
Напряжение на индуктивности опережает ток на 90 градусов;
Напряжение на ёмкости отстаёт от тока на 90 градусов.
Если строить векторную диаграмму, откладывая фазовые углы (смотри расчет к рисунку 10), то систему координат приходиться переносить в конец каждого вектора, чтобы отложить фазовый угол следующего вектора. Естественно, вектора можно строить через их проекции на оси координат.
Мощности в цепи переменного тока
В цепи переменного тока ток и напряжение изменяются по гармоническому закону, и между ними может быть ещё фазовый сдвиг 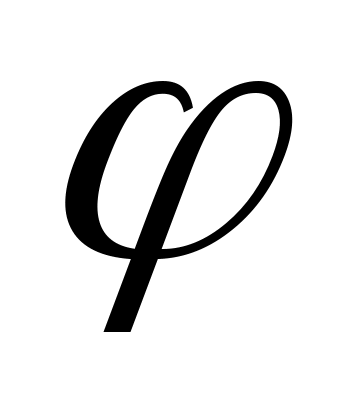 . Учитывая это, можно говорить о мгновенной мощности, мощности в конкретный момент времени t. . Учитывая это, можно говорить о мгновенной мощности, мощности в конкретный момент времени t.

Активная мощность
В результате простых тригонометрических преобразований (формула произведение синусов)получили два слагаемых
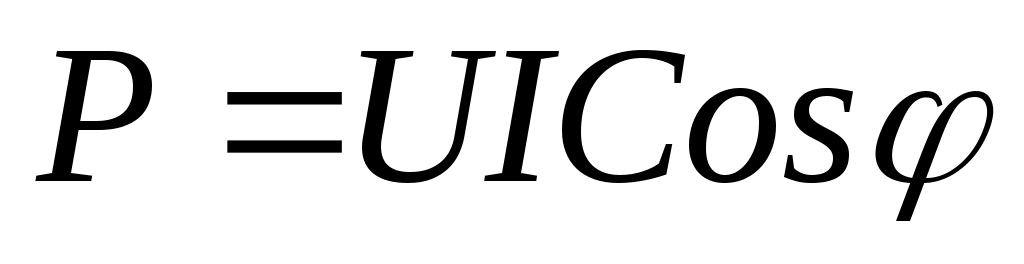 , - имеет постоянное значение , - имеет постоянное значение
Где 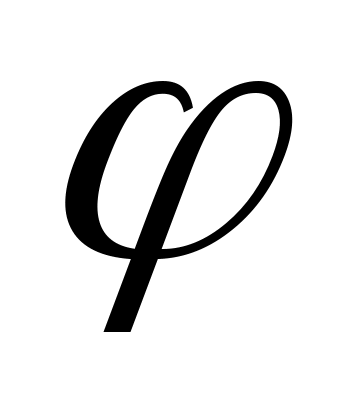 - фазовый угол между током и напряжением. Эта мощность получила название активная мощность. Сомножитель - фазовый угол между током и напряжением. Эта мощность получила название активная мощность. Сомножитель  называется «коэффициент мощности называется «коэффициент мощности  ». Если ток и напряжение совпадают по направлению, т.е. ». Если ток и напряжение совпадают по направлению, т.е.  , то , то  , и активная мощность максимальна (в цепи отсутствуют реактивные элементы). , и активная мощность максимальна (в цепи отсутствуют реактивные элементы).
Второе слагаемое:   - мощность, изменяющаяся с удвоенной частотой по отношению к частоте тока и напряжения. - мощность, изменяющаяся с удвоенной частотой по отношению к частоте тока и напряжения.

Рисунок 13. Мгновенная мощность в электрической цепи с индуктивностью
Из рисунка видно, что напряжение опережает ток, следовательно, цепь имеет индуктивный характер. Активная мощность приподнята над осью  на величину P. Относительно этого уровня гармонически изменяется мощность на величину P. Относительно этого уровня гармонически изменяется мощность  , то есть мощность Р это среднее значение за период Т мощности р. Положительное значение р соответствует мощности, потребляемой цепью (мощности отдаваемой источником в цепь), отрицательные значения р – мощности, возвращаемой источнику реактивным элементом (в данном случае индуктивностью). , то есть мощность Р это среднее значение за период Т мощности р. Положительное значение р соответствует мощности, потребляемой цепью (мощности отдаваемой источником в цепь), отрицательные значения р – мощности, возвращаемой источнику реактивным элементом (в данном случае индуктивностью).
Умножение на  это определение проекции одного вектора на другой, следовательно, переходя на комплексную плоскость это определение проекции одного вектора на другой, следовательно, переходя на комплексную плоскость
 , то есть , то есть

Реактивная мощность
Реактивная мощность – это мощность возвращаемая источнику энергии за счет обмена электоромагнитной энергией. Она обозначается Q.

Аналогично можно получить для реактивной мощности
 скалярное значение скалярное значение
В комплексом виде 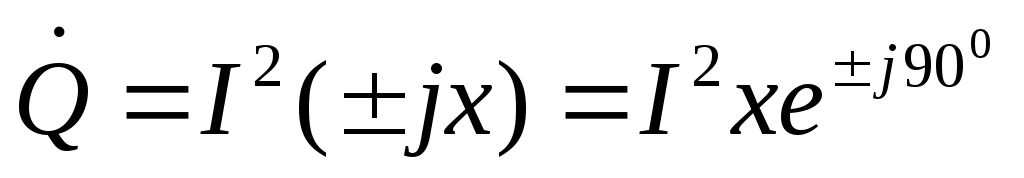
Обратите внимание, что в формулах определения Р и Q стоит действующее значение тока, а не комплексное, для которого вёлся расчет.
Единица измерения реактивной мощности Вар – Вольт-Ампер реактивный.
Полная мощность
Полная мощность это произведение действующих значений тока и напряжения
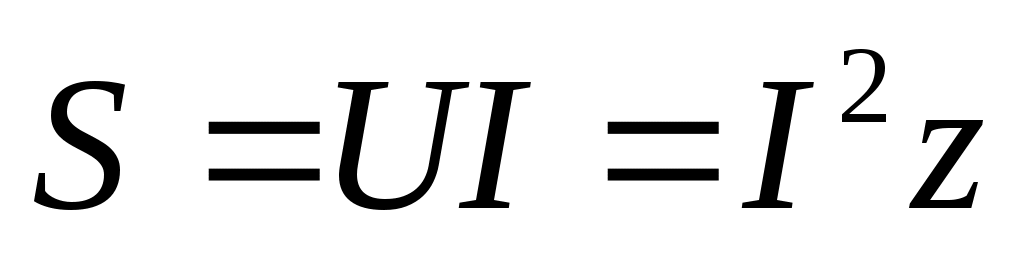 , ,
где  - полное сопротивление цепи. - полное сопротивление цепи.
Единица измерения полной мощности «ВА» - «Вольт-Ампер».
Треугольник мощностей
Так как 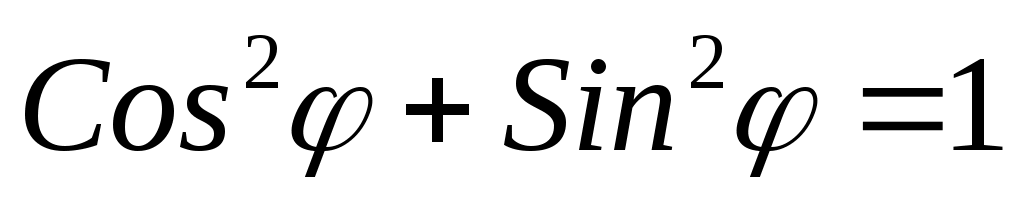 , то , то

и 
Полная, активная и реактивная мощности связаны таким же соотношением как стороны прямоугольного треугольника.
Для комплексных мощностей
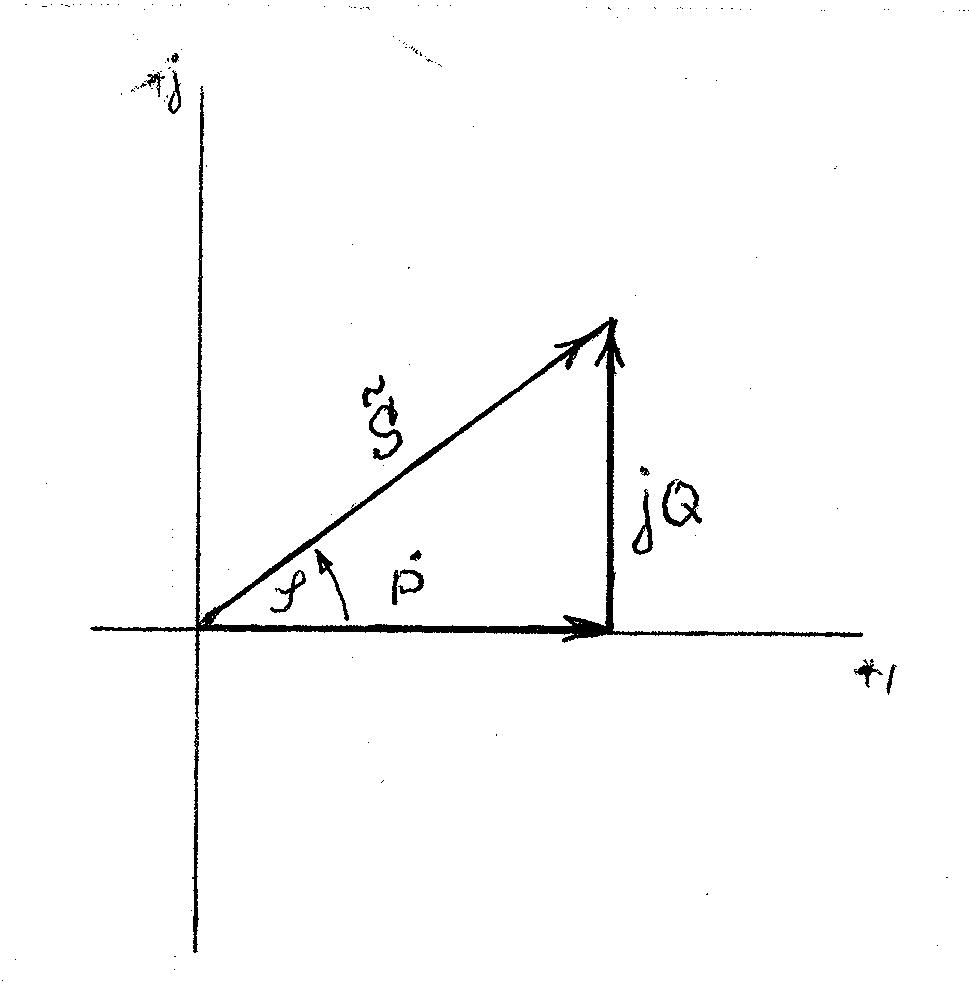
Рисунок 14. Треугольник мощностей
Если цепь будет иметь ёмкостной характер, то реактивная мощность

То угол 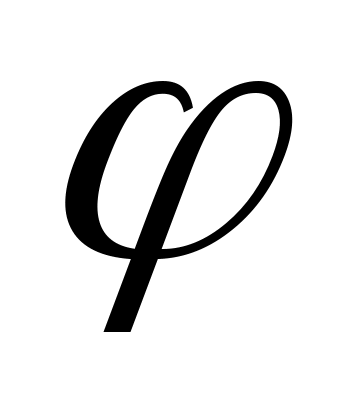 меньше нуля. Комплексная мощность (сложение векторов): меньше нуля. Комплексная мощность (сложение векторов):
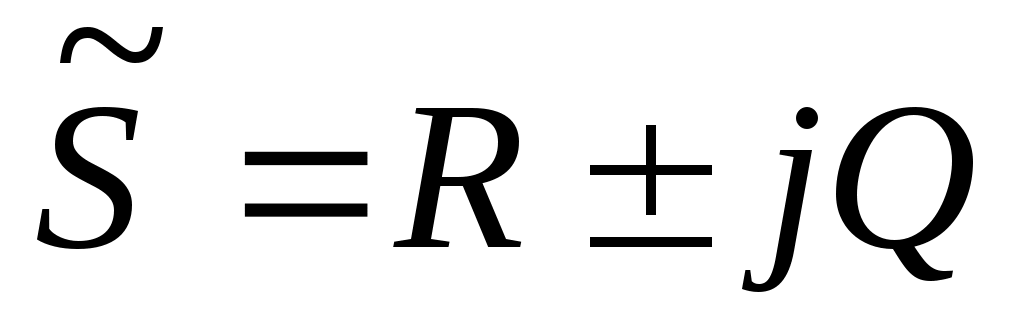
Знак «+» относится к индуктивности, «минус» - к ёмкости.
Баланс мощностей
Баланс должен выполняться по всем трём мощностям. Обычно он составляется для комплексной мощности

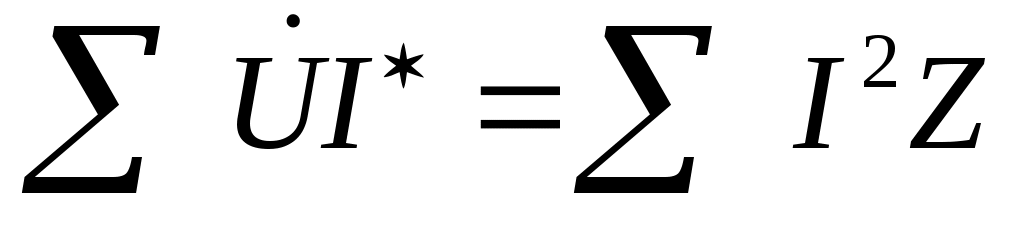
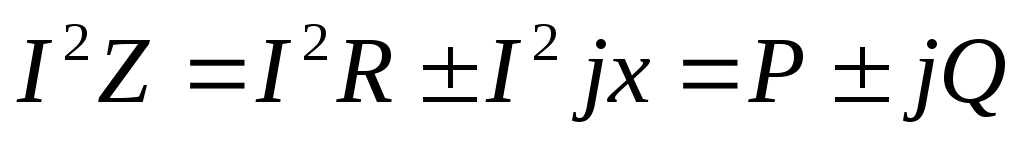
Где  спряжённый вектор вектору спряжённый вектор вектору  , то есть у , то есть у  меняется знак в показателе степени экспоненты в показательной форме записи комплексного числа меняется знак в показателе степени экспоненты в показательной форме записи комплексного числа 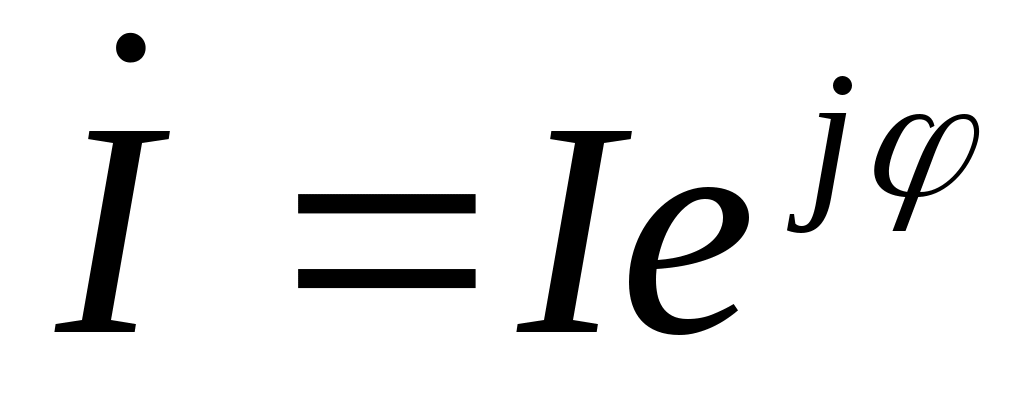 , сопряженный , сопряженный 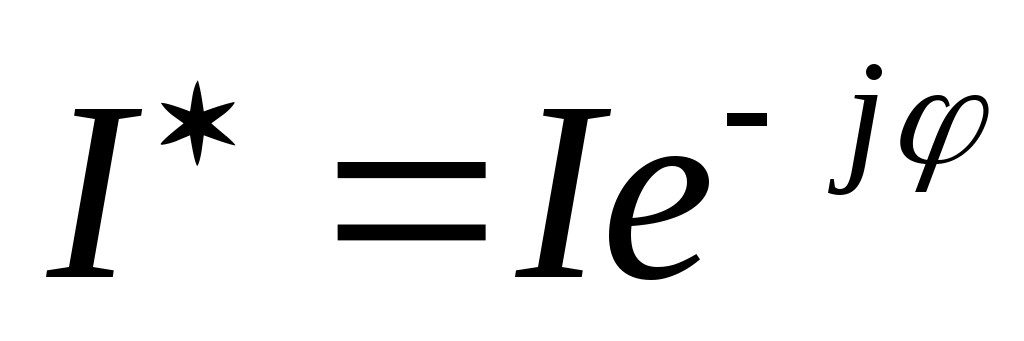
Заключение
В цепях с гармонически изменяющимся источником энергии возникает гармонически изменяющийся ток, которому оказывают сопротивление не только диссипативные элементы, но и частотно зависимые сопротивления - индуктивное и ёмкостное. Наличие реактивных сопротивлений приводит к фазовому сдвигу между током и напряжением. Чтобы не находить каждый раз фазовый сдвиг при расчете цепей, используется символический метод расчета (векторный), при котором расчет ведётся методами цепей постоянного тока, а фазовые углы получаются в процессе расчета.
Лекция 5 |
 Скачать 4.47 Mb.
Скачать 4.47 Mb. где
где


 ,
,  (А)
(А)




