метрология. Метрология. Мосты постоянного тока
 Скачать 22.2 Kb. Скачать 22.2 Kb.
|
|
Мосты постоянного тока Для измерения электрического сопротивления на постоянном токе используются одинарные или двойные мосты в зависимости от величины этого сопротивления. Одинарные мосты работают, как правило, на диапазонах от 10 до 106 Ом. Границы этого диапазона обусловлены со стороны малых значений величиной сопротивлений соединительных проводов и контактов, а со стороны больших – сопротивлением изоляции. Чувствительность мостовой схемы определяется значением измеряемого сопротивления и величиной напряжения питания. Измерение малых сопротивлений приводит к снижению чувствительности, которое может быть скомпенсировано увеличением напряжения питания. Однако, в результате ограничений на величину допустимой рассеиваемой мощности в плечах моста, постоянное увеличение напряжение питания мостовой схемы невозможно. Отмеченные недостатки отсутствуют в двойных измерительных мостах. Использование двойных мостов позволяет расширить нижний предел измеряемого сопротивления до 10–8 Ом. Для мостов постоянного тока нормирование основной погрешности осуществляется по относительной погрешности. Класс точности обозначается либо в виде одного числа c, и тогда предел допускаемой основной относительной погрешности определяется по одночленной формуле δ = с, либо в виде дроби с/d, и тогда – δ = ±[ с+ d (RК / RX ) – 1)], где RК – конечное значение сопротивления данного диапазона; RX – измеряемое сопротивление. 2. ЭДС источника с неизвестным внутренним сопротивлением измеряется дважды вольтметром на пределах 1 и 5В выходным сопротивлением 1 и 5 кОм соответственно. Класс точности вольтметра 0,5. Найти величину ЭДС и максимальные значения абсолютной и относительной погрешности, если показания вольтметра составляли 1 и 3 В. Основная инструментальная погрешность: Δинс = 𝛾∙𝑈н /100% на пределе 1В Δинс = 0,5*1/100% =± 0,005 В Относительная погрешность: δ = Δинс∙100% /𝑋изм = 0,005∙100% /1=0,5% на пределе 3В Δинс = 0,5*5/100% = ± 0,025 В Относительная погрешность: δ = Δинс∙100% /𝑋изм = 0,025∙100% /3= 0,83% 2) Методическая погрешность Действительные значения ЭДС по закону Ома при первом и втором измерениях: ε1 = Uизм1 + IV1Rв ε2 = Uизм2 + IV2Rв Подставляя значения измеренного напряжения, получаем: ε1 = 1 + IV1Rв ε2 = 3 + IV2Rв Отсюда: IV1 = U изм1 / RV1 = 1 мА IV2 = U изм2 / RV2 = 0,6 мА Подставляя в исходную формулу, получаем систему уравнений: ε1 = 1 + 1Rв ε2 = 3 + 0,6Rв Принимая ε1 = ε2, получаем: Rв = 5 кОм Отсюда, подставляя значение внутреннего сопротивления Rв в любое выражение, получаем ε = 1 + 1Rв = 6 В. Измеренные значения U изм1 = ε изм1 = 1 В и U изм2 = ε изм2 = 3 В Абсолютную погрешность определяем по формуле: ∆εм=εизм - ε Для первого измерения ∆εм=1−6=±5 В Для второго измерения ∆εм=3−6=±3 В Относительную погрешность определяем по формуле: 𝛿εм=(∆εм/ε )100% Для первого измерения: 𝛿εм=(±5/6)100%=83% Для второго измерения: 𝛿εм=(±3/6)100%=50% Выбирая из двух измерений по п.п. 1) и 2) значение большей абсолютной инструментальной и методической погрешностей, суммарную максимальную погрешность измерения определим по формуле: 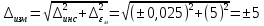 Относительная погрешность при этом: 𝛿изм=(∆изм/ε)100%=(5/6)100%=83% Таким образом, ЭДС ε = 6 В; максимальное значение абсолютной погрешности Δизм = ±0,025 В; максимальное значение относительной погрешности δизм = 83%. 3. Определить значения методической и инструментальной погрешности косвенного измерения сопротивлений 500 кОм и помощью амперметра и вольтметра по двум возможным схемам. Сопротивление амперметра 20 Ом, сопротивление вольтметра 10 кОм; напряжение источника питания 1 В; конечные значения диапазонов измерения амперметра: 2 мА; вольтметра 1 В. Классы точности: амперметра 0,5, вольтметра 1. Нарисовать схемы. 1) Методическая погрешность обусловлена влиянием измерительных приборов с сопротивлением RА и RV на значение измеряемого сопротивления Rизм. Относительная методическая погрешность измерения сопротивления: 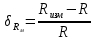 где Rизм – измеряемое значение сопротивления; R – действительное значение сопротивления. Для схем а) и б) действительное значение R1 = 100 Ом. Измеряемое значение сопротивления по закону Ома для схемы а): RA-V = RA + RV = 20 Ом + 10 кОм = 10,02 кОм; 1/Rизм = 1/ RA-V + 1/R1 = 0,01 + 0,002 = 0,012 отсюда Rизм = 83 кОм для схемы б): 1/RV-1 = 1/RV + 1/R1 = 0,1 + 0,002 = 0,102 кОм, Отсюда RV-1 = 10 кОм; Rизм = RV-1 + RА = 10 + 0,02 = 10,02 кОм. Относительная методическая погрешность измерения сопротивления по схеме а): 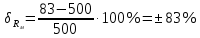 Абсолютная погрешность при этом: 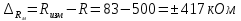 по схеме б): 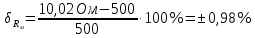 Абсолютная погрешность при этом: 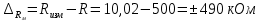 2) Абсолютная приведенная погрешность (класс точности) амперметра по условию задачи 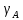 = 0,5%, вольтметра – = 0,5%, вольтметра – 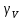 = 1%. = 1%.Абсолютная погрешность измерения амперметроме: 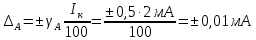 Абсолютная погрешность измерения вольтметром: 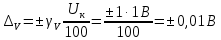 Суммарная относительная погрешность измерительного комплекса: 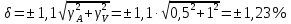 Абсолютная инструментальная погрешность измерения сопротивления: 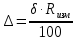 По схеме а) ∆ = 1,23∙ 83 / 100 = ±1,02 кОм По схеме б) ∆ = 1,23∙10,02 / 100 = ±0,12 кОм 4. Найти доверительный интервал относительной случайной погрешности результата 5-ти кратного измерения сопротивления резистора, если оценка среднего квадратического отклонения равна 0,92 Ом. Закон распределения случайных погрешностей нормальный. Доверительную вероятность принять равной 0,9; 0,95; 0,98. Среднее арифметическое значение результата измерения 68,8 Ом. Т.к. закон распределения результатов измерений нормальный, то с его использованием находят квантильный множитель zp при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности составляют ∆ = ±zp⋅Sx. По таблице квантилей стандартного нормального закона распределения находим при заданных вероятностях квантильные множители: zp (0,9) = 1,28; zp (0,95) = 1,645; zp (0,98) = 2,05. Таким образом, доверительные интервалы составят: ∆ (0,9) = ± 1,28∙0,92= ± 1,178; ∆ (0,95) = ± 1,645∙0,92 = ±1,513; ∆ (0,98) = ± 2,05∙0,92 = ± 1,886. 5. Класс точности цифрового вольтметра 1/0,5. Определить абсолютную погрешность и записать результат, если на диапазоне измерения 0 … 1 В вольтметр показывает 0,572 В. Предельная основная погрешность цифрового вольтметра: 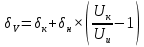 , ,где δк = 1 – погрешность вольтметра при измерении конечных значений напряжения; δн = 0,5 – погрешность вольтметра при измерении начальных значений напряжения; Uк = 1 В – предел измерения вольтметра; Uи = 0,572 В – измеренное значение напряжения. Относительная погрешность вольтметра: γV = 1 + 0,5 ( 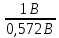 – 1) = ± 1,122%. – 1) = ± 1,122%. Абсолютную погрешность: ∆U = Uи ∙ γV / 100, Отсюда ∆U = 0,572∙(±1,122) /100 = ±0,0064 результат измерения: U = (0,572 ± 0,006) В. |
