Альтернативная математика. АльтерМат. Муниципального образования городской округ Симферополь Республики Крым Исследовательский проект Альтернативные направления математики
 Скачать 259.54 Kb. Скачать 259.54 Kb.
|
|
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №5 им.85-го АСП» Муниципального образования городской округ Симферополь Республики Крым Исследовательский проект «Альтернативные направления математики» Работу выполнил: Маньковский Даниэль Учащийся 9-Б класса МБОУ «СОШ№5 им.85-го АСП» г.Симферополь Научный руководитель: Бобрик Оксана Петровна Учитель алгебры и геометрии МБОУ «СОШ№5 им.85-го АСП» г.Симферополь Симферополь 2022 Содержание Введение……………………………………………………………………..3 Глава 1 1)Коротко о Евклидовой и Неевклидовой геометрии…..4 2)Сферическая геометрия……………………………………………….4 Глава 2 Биография Римана………………………………………………………..5 Геометрия Римана…………………………………………………..6 Биография Лобачевского…………………………………………6-7 Геометрия Лобачевского…………………………………………….7 Глава 3 Наглядные различия между 3 разделами геометрии………..8 Топология и топологические эксперименты………………..9-10 Вывод…………………………………………………….11 Источники информации…………………………………..12 Введение Математика-царица наук. Очевидно, что царица наук многогранна и во многом сложно понять ее неоднозначную натуру. Большинство ошибочно считают, что математика делится на базовую алгебру и базовую геометрию, для многих также не секрет, что существует углубленный курс математики(профильный) и математический анализ. Однако математика куда глубже и интереснее. Сейчас мы рассмотрим эту науку с той стороны, о которой не расскажут в школе. Актуальность. В наше время дети теряют интерес к науке. Новые математические направления могут заинтересовать современных подростков Цели и задачи проекта: Выяснить, какие существуют отличные от школьной программы направления математики. Доказать, что математика намного интереснее, чем кажется Разобрать основные отличия школьной программы математики от альтернативной Расширить кругозор и усилить воображение Глава 1 Возьмем геометрию. Она делится на 2 основных раздела: евклидова и неевклидова геометрия. Евклидова геометрия изучает фигуры на плоскости, с условием, что они никак не меняются от влияния внешних факторов. А вот неевклидовой геометрии нет никакой разницы до правил, в ней все что угодно может стать чем угодно. Сегодня мы узнаем: почему нам врали и сумма углов треугольника на самом деле не равна 180 градусам? Действительно ли параллельные прямые никогда не пересекаются? И чем человек, похож на спиннер? Думаю мне удалось вас заинтриговать. Начнем пожалуй с чего-то попроще для понимания – Сферической геометрии. Сферическая геометрия – это геометрия занимающаяся изучением геометрических фигур на поверхности сферы. Для начала стоит определиться зачем она нужна. Все очень просто, без нее бы просто не существовало ни географии, ни астрономии. Почему? Элементарно. Эти науки изучают Землю(в случае с географией) и другие планеты(соответсвенно в случае с астрономией), а планеты имеют форму эллипса – по сути сферы, приплюснутой у полюсов. Но, как наверное и в обычной геометрии, самая интересная фигура в сферической – треугольник, или если правильно – сферический треугольник. По сути своей это треугольник, растянутый по поверхности сферы. На картинке вы видите пример сферического треугольника. Люди с хорошим глазомером уже наверняка заметили, что с углами определенно что-то не так. Это правда. Сумма углов треугольника не имеет постоянного значения, в отличие от треугольника на плоскости. Она определяется по довольно простой формуле. Она всегда меньше 3п и больше п. Площадь такого треугольника определяется по формуле Жирара Вообще сферическими треугольниками занимается Сферическая тригонометрия. Знание формул сферической тригонометрии необходимо при решении таких задач, как, например, преобразование координат из одной системы небесных координат в другую, расчёт долготы центрального меридиана планеты Солнечной системы, разметка солнечных часов и точное направление спутниковой антенны («тарелки») на нужный спутник для приёма каналов спутникового телевидения. С этим разобрались, пойдем далее. Глава 2 Биография Римана Риман родился в Брезеленце – деревеньке в окрестностях Данненберга в Королевстве Гановер (ныне – Федеративная республика Германии). Фридрих Бернхард Риман, его отец, был бедным лютеранским священником, принимавшим участие в Наполеоновских войнах. Его мать, Шарлотта Эбелль, рано умерла. Бернхард был вторым из шестерых детей в семье. С ранних лет мальчик демонстрировал потрясающие математические способности и невероятные успехи в счёте, однако ребёнком он был застенчивым и пережил немало нервных срывов. Он был патологически робким человеком и страдал от боязни перед публичными выступлениями.  Геометрия Римана На самом деле, Евклидова геометрия от неевклидовой отличается тем, что Евклидова изображается на плоскости с нулевой кривизной – как этот стол, а неевклидова на плоскости с положительной кривизной – как этот мячик, или отрицательной – как кубок. Сферическая геометрия относиться к положительной. Тогда рассмотрим ее “сестру по кривизне” – Геометрию Римана, также называемую эллиптической. Я думаю все знают, что такое эллипс. Напомню, это круг, приплюснутый у полюсов. Именно из этого выходит главное отличие Римановской геометрии от Сферической. Любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения. При отождествлении противоположных точек сферы получается проективная плоскость, геометрия которой удовлетворяет аксиомам геометрии Римана. Не буду вдаваться в подробности. Это было сказано лишь для того, чтобы не сложилось мнение, что Сферическая и Эллиптическая геометрия идентичны. Также, из-за кривизны параллельные прямые в этой геометрии пересекаются. Я вернусь к этому позже Биография Лобачевского Никола́й Ива́нович Лобаче́вский (20 ноября (1 декабря) 1792, Нижний Новгород — 12 (24) февраля 1856, Казань) — российский математик, один из создателей неевклидовой геометрии, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии»[3]. Лобачевский в течение 40 лет преподавал в Императорском Казанском университете, в том числе 19 лет руководил им в должности ректора; его активность и умелое руководство вывели университет в число передовых российских учебных заведений. По выражению Н. П. Загоскина, Лобачевский был «великим строителем» Казанского университета[4].  Геометрия Лобачевского От положительной кривизны перейдем к отрицательной. Я думаю многие о ней наслышаны. Сейчас пойдет речь о Геометрии Лобачевского. По моему личному мнению, самая интересная из представленных сегодня. По- другому, ее также называют Гиперболической геометрией. Сегодня, я остановлюсь на самом, на мой взгляд, интересном отличии этой геометрии от школьной. В школе нам всем рассказывали такую аксиому: На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной. Все ее помнят. Однако в Геометрии Лобачевского она заменяется на: Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Глава 3 Проще увидеть. Наглядные различия между 3 разделами геометрии 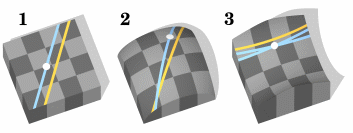 Школьная Геометрия Геометрия Римана Геометрия Лобачевского. Действительно, в этих направлениях геометрии законы совсем другие. Ради интереса я решил составить таблицу, где наглядно показал разницу в теоремах для этих 3 направлений
Топология и топологические эксперименты Казалось бы, я уже перевернул ваши взгляды на математику, но и это еще не все. Теперь, наверное самое красивое альтернативное направление математики. Топология. Наука, задачи которой звучат довольно скучно, если не вдаваться в подробности. Она изучает: в самом общем виде — явление непрерывности; в частности — свойства пространств, которые остаются неизменными при непрерывных деформациях. Например, связность, ориентируемость, компактность. Звучит сложно. Так что мы разберем лишь интересное. Вот, вы можете вывернуть этот мяч наизнанку? (проводится эксперимент, экзаменаторы убеждаются, что мяч вывернуть невозможно). А в топологии, с этим нет никаких проблем. Можете ли вы принять, что пончик и кружка – одно и тоже? А человек совершенно не отличим от спиннера? Дело в том, что в топологии, главным в любом материальном теле является количество в нем сквозных отверстий. К примеру, у пончика, или как такую форму называют в топологии, у тороида и у кружки, по одной дырке. Следовательно, топологически они равны, или гомеоморфны. То же самое и в случае с человеком и спинером. Если посчитать, то у человека четыре сквозных отверстия. Уши являются впадинами, поэтому за сквозные отверстия не считаются. И выходит, что человек гомеоморфен спиннеру. Завершить рассказ о топологии хочется еще одним экспериментом.(проводиться эксперимент с экзаменаторами). Образуйте из большого и указательного пальца одной руки кольцо, после чего зацепитесь таким же кольцом, но уже другой рукой изнутри. Попробуйте разьединить руки, не отрывая пальцы друг от друга. Это невозможно? Вы правы, в нашей материи – это невозможно. Но вот в мире топологии, возможно многое, и даже это. Взгляните: 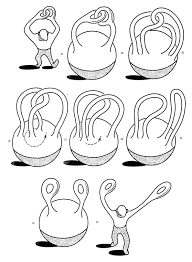 Вывод Математика- интересная и многогранная наука. Сегодня мы познакомились с ее разделами, которых нет в школьной программе. Это довольно странно, ведь мы живем не в плоском мире, а неевклидова геометрия, предоставляет нам только его. Мне кажется, всем стоит хоть раз окунуться в этот неизведанный мир математики за пределами нулевой плоскости. Наша вселенная огромна и плохо изучена, так что, на самом деле стоит «изобретать велосипед», ведь, вполне возможно, что ты найдешь что-то новое в этом потоке неизученной информации. Источники: https://youtu.be/CN_hdnnvPdo https://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F_%D0%A0%D0%B8%D0%BC%D0%B0%D0%BD%D0%B0 https://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F_%D0%9B%D0%BE%D0%B1%D0%B0%D1%87%D0%B5%D0%B2%D1%81%D0%BA%D0%BE%D0%B3%D0%BE https://ru.wikipedia.org/wiki/%D0%A1%D1%84%D0%B5%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F https://ru.wikipedia.org/wiki/%D0%A2%D0%BE%D0%BF%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%8F |
