контрольная работа. На основании данных, представленных в таблице (150 Х1, Х3, Х5)
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Вариант №7. На основании данных, представленных в таблице: (1-50; Х1, Х3, Х5) 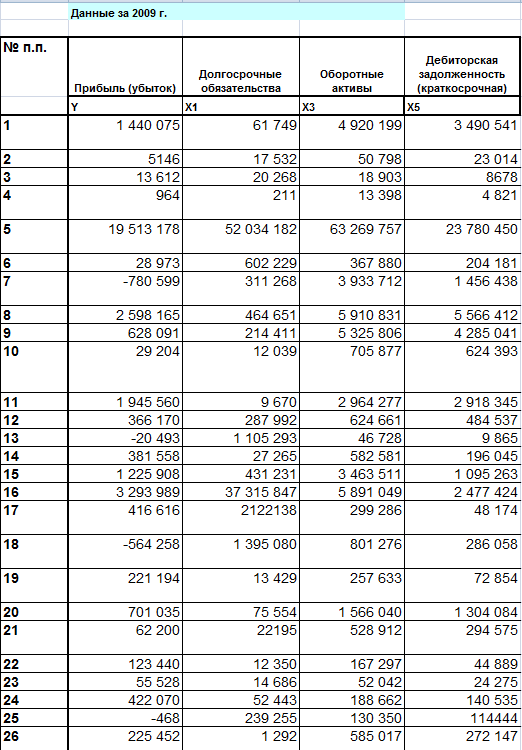  У – зависимая переменная (прибыль/убыток) Х1 – Долгосрочные обязательства Х3 – Оборотные активы Х5 – Дебиторская задолженность Х1, Х3, Х5 – зависимые, объясняющие переменные Количество наблюдений n=50, количество объясняющих переменных m=3. Постройте диаграммы рассеяния, представляющие собой зависимости Y от каждого из факторов X. Сделайте выводы о характере взаимосвязи переменных. 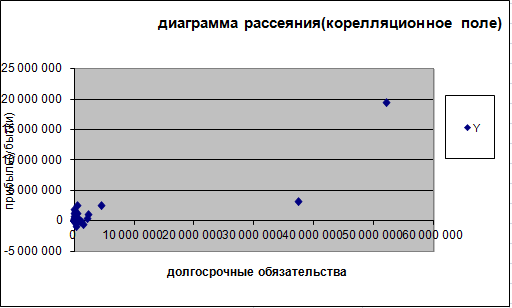 Рис.1. Диаграмма рассеяния, показывающая зависимость прибыли (убытка) от долгосрочных обязательств.  Рис.2. Диаграмма рассеяния, показывающая зависимость прибыли (убытка) от оборотных активов. 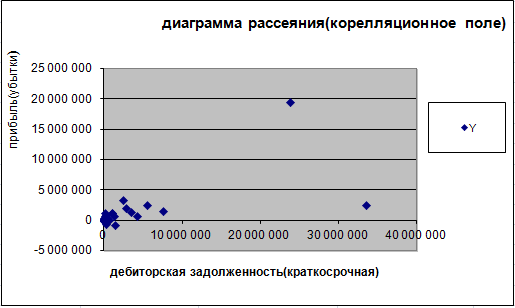 Рис.3. Диаграмма рассеяния, показывающая зависимость прибыли (убытка) от дебиторской задолженности. Вывод: по диаграмме рассеяния для x1 наблюдаем тесную прямую, линейную связь прибыли с долгосрочными обязательствами. Имеются аномальные наблюдения. По диаграмме рассеяния для x3 наблюдаем прямую, линейную со слабой зависимостью связь прибыли с оборотными активами. Имеются аномальные наблюдения. По диаграмме рассеяния для x5 наблюдаем нелинейную связь прибыли с дебиторской задолженностью. Имеются аномальные наблюдения. Осуществить двумя способами выбор факторных признаков для построения регрессионной модели: а) на основе анализа матрицы коэффициентов парной корреляции, включая проверку гипотезы о независимости объясняющих переменных (тест на выявление мультиколлинеарности Фаррара-Глоубера); б) с помощью пошагового отбора методом исключения. а) Получим матрицу коэффициентов парной корреляции. Для этого используем инструмент Корреляция (надстройка Анализ данных Excel). Табл.1. Матрица коэффициентов парной корреляции.
Анализ матрицы коэффициентов парной корреляции начинаем с анализа первого столбца матрицы, где расположены коэффициенты корреляции, отражающие тесноту связи зависимой переменной Объем реализации с включенными в анализ факторами. Анализ показывает, что зависимая переменная, т.е. объем реализации, имеет тесную связь с оборотными активами (ryx3= 0.912), с долгосрочными обязательствами (ryx1= 0.867) и с дебиторской задолженностью (ryx5= 0.654). Затем переходим к анализу остальных столбцов матрицы с целью выявления коллинеарности. Факторы х1 и х3 тесно связаны между собой (rх1х3= 0.76), что свидетельствует о наличии коллинеарности. Из этих двух переменных оставим Х3 – оборотные активы, так как rх3у= 0.91> rх1у= 0.87. В нашем примере из двух тесно связанных друг с другом факторов Х1 и Х3 (rх1х3= 0.76) один, Х5, был исключен. Так как по данной матрице мы затрудняемся выбрать связь факторов, построим матрицу частных корреляций. Используем программу VSTAT. Табл.2. Матрица частных корреляций.
Для выявления мультиколлинеарности факторов Х1, Х3, Х5 выполняют тест Феррара-Глоубера. Построим матрицу межфакторных корреляций R1 и найдем её определитель.  Оставляем только 2 фактора Х1 и Х3, которые наиболее тесно связаны с Y. Т.к. определитель 0,06 стремится к 0, то все факторы между собой зависимы и, следовательно, наблюдается мультиколлениарность. б) с помощью пошагового отбора методом исключения. Воспользуемся программой VSTAT – Регрессионный анализ – Пошаговая регрессия 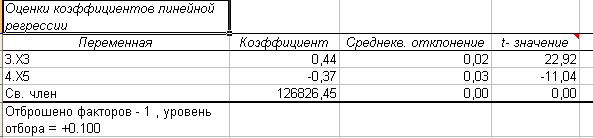 Табл.3. Пошаговая регрессия. Табл.3. Пошаговая регрессия.С помощью пошагового отбора методом исключения в программе Vstat, были выбраны параметр Х3(оборотные активы). Построить уравнение множественной регрессии в линейной форме с выбранными факторами. Дать экономическую интерпретацию коэффициентов модели регрессии. Для построения уравнения множественной регресии, необходимо рассчитать регрессию по отобранным факторам. Для этого воспользуемся программой MS Excel (данные→ анализ данных→ регрессия). Табл.4. Множественная регрессия 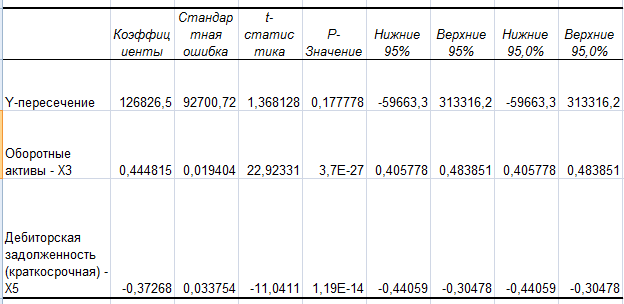 На основании полученных данных составляем уравнение множественной регрессии в линейной форме. Y = 126826,5 + 0,444815 х3- 0,37268 х5. Экономический смысл коэффициентов регрессии: при изменении оборотных активов (х3) на 1 млн.руб. прибыль изменится в противоположную сторону на 0,445 млн.руб. При изменении дебиторской задолженности (х5) на 1 млн.руб. прибыль уменьшится на -0,373 млн.руб. 4.Дайте сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности, β- и Δ-коффициентов. Воспользуемся программой Vstat. Табл.5. Оценка коэффициентов.  
Вывод: при изменении долгосрочных обязательств(х1) на 1%, прибыль меняется в ту же сторону на 0,13 %, изменение неэластично. При изменении оборотных активов(х3) на 1%, прибыль меняется в ту же сторону примерно на 1,44%, изменение эластично. Изменение дебиторской задолженности ( х5) – не эластично, так как она равна -0,70. При изменении фактора х1 на 1 СКО, прибыль меняется в ту же сторону на 0,14 своего СКО. Так же и при изменении фактора х3 на 1 СКО Прибыль изменится в ту же сторону на 1,36 своего СКО. Средняя доля влияния фактора х1 на у составляет 0,09; фактора х3 – 0,91. Наиболее сильное влияние на Прибыль (у) оказывает Оборотные активы (х3), так как Э=1,44; β=1,36; ∆=0,91. 5) Рассчитайте параметры линейной парной регрессии для наиболее подходящего фактора Рассчитаем параметры с помощью программы VSTAT. Наиболее подходящий фактор х3 – Оборотные активы.
y =26398,24 + 0,25x3 + e. 6) Оцените качество построенной модели с помощью коэффициента детерминации, средней относительной ошибки аппроксимации и F-критерия Фишера. 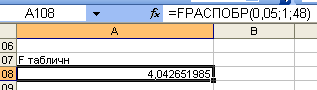
Коэффициент детерминации = 0,831. Это говорит о том, что около 83% случайных колебаний учтено в построенной модели и обусловлено случайными колебаниями, включенных в неё факторов. Не учтено в модели влияние 1-0,831=0,169 примерно 7%. F=236,387 Fтаб= Fтаб(0,05;1;48)=4,043. F больше Fтаб., следовательно, уравнение статистически значимое. Средняя относительная ошибка аппроксимации=0,912 стремится к 1, следовательно, построенная модель качественная. Проверьте выполнение условия гомоскедастичности. Для проверки условия гомоскедастичности сначала значение переменной Y упорядочиваем по возрастанию фактора Х с помощью инструмента Данные – Сортировка в Microsoft Excel. Далее из середины упорядоченной совокупности убираем С=(1/4)*50=12 центральных значений.
Для каждой из полученных совокупностей выполняем регрессионный анализ и находим две остаточные суммы квадратов. Табл.6. Остаточные суммы квадратов
Затем вычислим  Воспользуемся F-критерием Фишера: Fтабл=2,271892889 Так как F табл. > R – остатки гомоскедастичны. 8) Используя результаты регрессионного анализа, ранжируйте компании по степени эффективности. Для ранжирования берем столбец с названиями компаний и столбец с расчетным значением прибыли и сортируем по возрастанию. Табл.7. Ранжировка по возрастанию.
Вывод: компанией с самой маленькой прибылью (26830,3 млн.руб.) является Кировское Нефтегазодобывающее Управление, а с самой большой прибылью (16089382,5 млн.руб.) является Акционерная нефтяная Компания Башнефть. 9) Осуществите прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора Хj составит 80% от его максимального значения. Представьте на графике фактические данные Y, результаты моделирования, прогнозные оценки и границы доверительного интервала. y=26398,24+0,25x3+e а) точечный прогноз Х =0,8* х(max) = 0,8 * 63269757 = 50615805,6 б) точечный прогноз У = 26398,24+0,25*Х У = 26398,24 + 0,25*50615806 = 12680349,64 в) интервальный прогноз У:  найдем ошибку прогнозирования: U=Se*tтабл =1957487,488 t табл = 1,677224197 Se=1167099.48 Нижняя граница: У - U = 12680349,64 – 1957487,49 = 10722862,15 Верхняя граница: У + U = 12680349,64 + 1957487,49 = 14637837,13  Составить уравнения нелинейной регрессии: - гиперболической; - степенной; - показательной. 11. Привести графики построенных уравнений регрессии. Составим уравнения нелинейной регрессии с помощью программы VSTAT.
Вывод: Степенная, показательная и гиперболическая функции не построены (не идентифицированы), но в качестве лучшей указана функция: Выбрана функция Y(X)= +406402.483+0.000*X**4 а) гиперболическая модель: у = 1694324,77 – 2572512035*Х – линейная у = 1694324,77 - 2572512035/Х – нелинейная   б) степенная У = 4.798+0.226*X – линейная У = 62805,84*х в степени 0,226 нелинейная 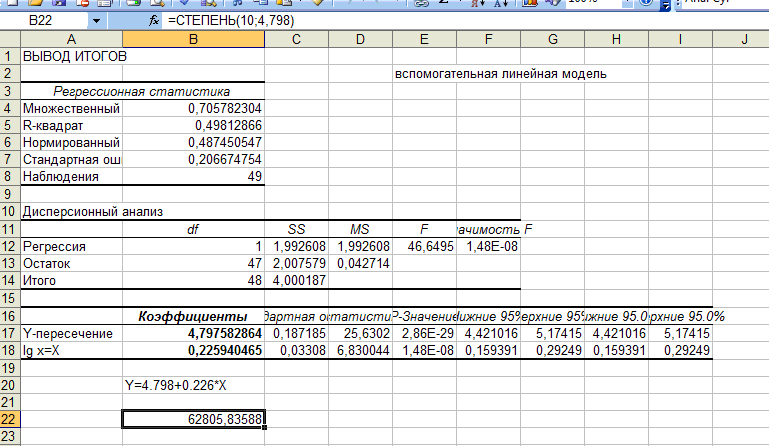  в) показательная у = -46242556,16+7917760,32*х -линейная у = 7,66504183 * 6,898602351˟- нелинейная 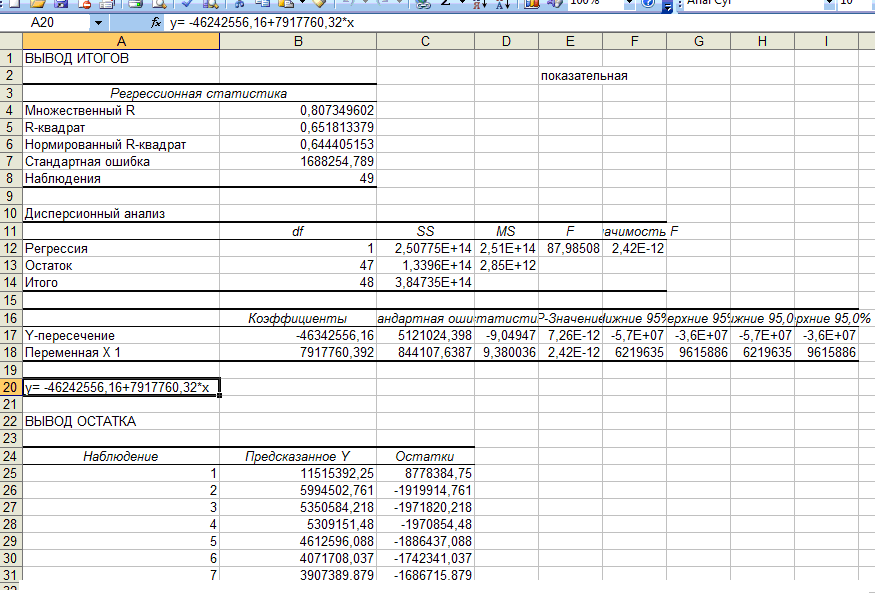 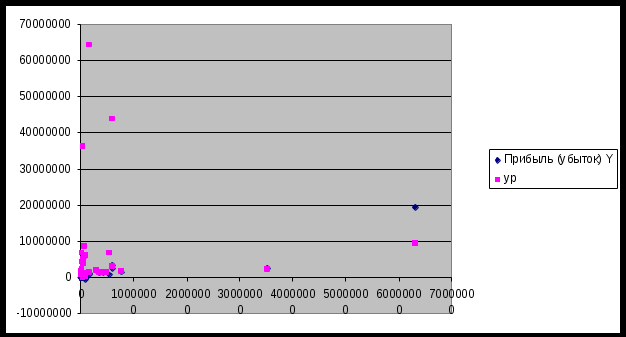 12) Для нелинейных моделей найдите коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравните модели по этим характеристикам и сделайте выводы о лучшей модели. Табл.8. Сравнение нелинейных моделей.
Лучшая из моделей – показательная. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
