Декартова система координат. На плоскости, другими словами прямоугольной координатной плоскостью
 Скачать 467.6 Kb. Скачать 467.6 Kb.
|
|
Вы уже знакомы с прямоугольной системой координат на плоскости, другими словами прямоугольной координатной плоскостью. Такую систему координат задают две взаимно перпендикулярные прямые, на каждой из которых выбрано направление и величина единичного отрезка. Эти прямые называют осями абсцисс и ординат. Точку пересечения осей называют точкой начала координат.  Прямоугольную систему координат на плоскости обозначают Оху. Каждой точке плоскости сопоставляется только одна пара чисел, которые называют её координатами. Для определения координат, из точки нужно провести перпендикуляры к осям, тем самым мы и получим абсциссу и ординату точки. Определение: Если же через точку пространства проведены три попарно перпендикулярные прямые, а на каждой из них выбрано направление и единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве. Прямые с выбранными на них направлениями называют осями координат, а точку их пересечения — началом координат. Как и на плоскости её обычно обозначают буквой О. 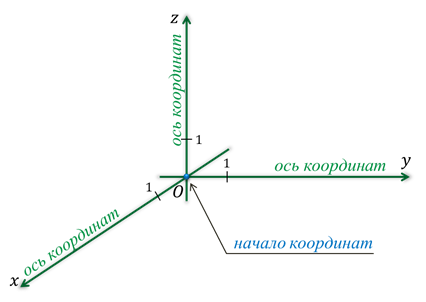 Оси координат обозначают так: Ох, Оу, Оz. И называют осью абсцисс, осью ординат и, новым является название третьей оси, ось аппликат. 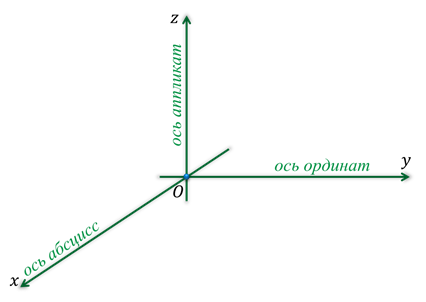 Прямоугольную систему координат в пространстве обозначают Охуz. Через каждые 2 оси координат проходят координатные плоскости: Оху, Оуz и Охz. Всего таких плоскостей 3. 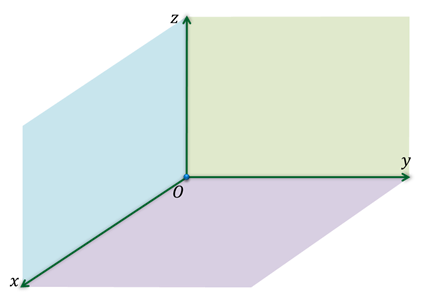 Каждая ось делится точкой О на два луча. В соответствии с этим, лучи, направление которых совпадает с направлением оси, называют положительными полуосями, а оставшиеся лучи — отрицательными полуосями.  Каждой точке пространства сопоставляется только одна тройка чисел, которые называют её координатами. Их определяют аналогично тому, как это делали на плоскости. Только через точку М проводят плоскости перпендикулярные координатным осям. 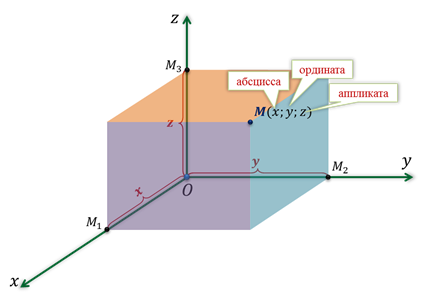 Точки пересечения проведённых плоскостей с осями координат назовём М1, М2 и М3. Первая координата точки М, то есть её абсцисса, равна длине отрезка ОМ1. Вторая координата, которую называют ординатой, равна длине отрезка ОМ2. Ну, а третья координата, а точнее аппликата, равна длине отрезка ОМ3. Координаты точки записывают в скобках, при этом первой записывают абсциссу, второй — ординату, а третьей — аппликату. В данном случае точки М1, М2 и М3 являются точками положительных полуосей, поэтому и координаты точки М будут положительными числами. Рассмотрим примеры различного расположения точек в прямоугольной системе координат. Задание: определить координаты точек А, В, С, D, Е и F. 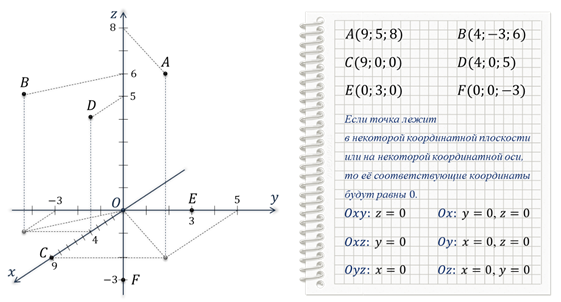 После выполнения этого задания можно сделать вывод о том, что если точка лежит в некоторой координатной плоскости или на некоторой координатной оси, то её соответствующие координаты будут равны нулю. Так если точка лежит в координатной плоскости Оxy, то её аппликата равна нулю. Если точка лежит в координатной плоскости Оxz, то её ордината равна нулю. И если точка лежит в координатной плоскости Оyz, то её абсцисса равна нулю. Ну, а в случаях, когда точка лежит на одной из осей, только одна координата является ненулевой. Задание: По координатам точек 𝐴(3;−1;0), 𝐵(0;0;−7), 𝐶(2;0;0), 𝐷(−4;0;3), 𝐸(0;−1;0), 𝐹(1;2;3), 𝐺(0;5−7), 𝐻(−√5;√3;0) определить, какие из них лежат на той или иной координатной оси или в той или иной координатной плоскости. Решение:  Задание: найти координаты проекций точки 𝐴(2;−3;5) на каждую из координатных плоскостей и на каждую из координатных осей. 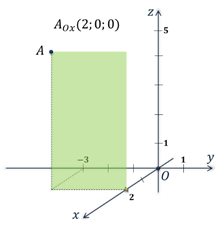 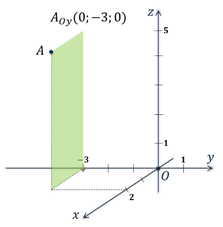 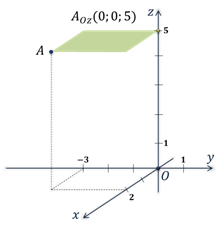 Далее найдём координаты проекций точки А на координатные плоскости. Проекцией точки А на координатную плоскость Оху является основание перпендикуляра, проведённого из точки А к данной координатной плоскости. При этом координаты полученной проекции будут такими же как у точки А, только аппликата станет равной нулю. Аналогично получим проекцию точки А на координатную плоскость Оуz. Проведём перпендикуляр из данной точки к данной координатной плоскости. Его основание и является проекцией точки А на плоскость Оуz. Координаты данной проекции равны координатам точки А, только абсцисса равна нулю. Ну, а проекция точки А на координатную плоскость Охz будет иметь координаты 2, 0, 5.  Так мы с вами нашли координаты проекций точки А на координатные оси и на координатные плоскости. Задание: 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1− куб; 𝐴(0;0;0), 𝐵(0;0;1), 𝐷(0;1;0), 𝐴1 (1;0;0). Найти координаты точек 𝐶, 𝐵1, 𝐶1 и 𝐷1. Решение: Изобразим прямоугольную систему координат. Отметим точки, являющиеся вершинами куба, координаты которых известны. 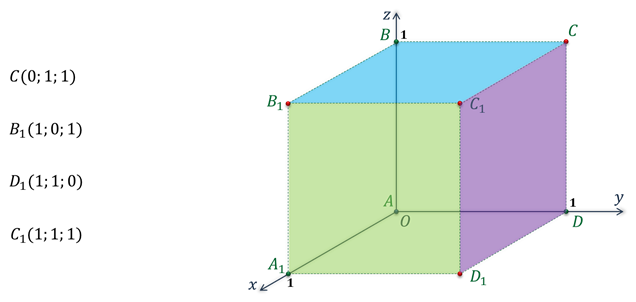 |
