лаба. Национальный исследовательский университет московский энергетический институт кафедра диагностических информационных технологий
 Скачать 173.09 Kb. Скачать 173.09 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ КАФЕДРА ДИАГНОСТИЧЕСКИХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ Типовой расчет. по дисциплине Метрология информационно-измерительных систем Выполнил студент: Дроздов А.С. Группа А-04м-22 Принял: доцент Долгачева Е.А. Москва 2022 Задание МИС_Рз2-4. Рассчитать цифровой фильтр Баттерворта верхних частот восьмого порядка с частотой среза fс = 100 Гц. Необходимо: 1. Выбрать структурную схему фильтра и частоту дискретизации fд. 2. Пояснить порядок работы схемы фильтра. 3. Найти аналитическое выражение для амплитудно-частотной характеристики фильтра  A(f ) и построить её график. A(f ) и построить её график.1. Выбрать структурную схему фильтра и частоту дискретизации fд. Структурная схема фильтра показана на рисунке 1. 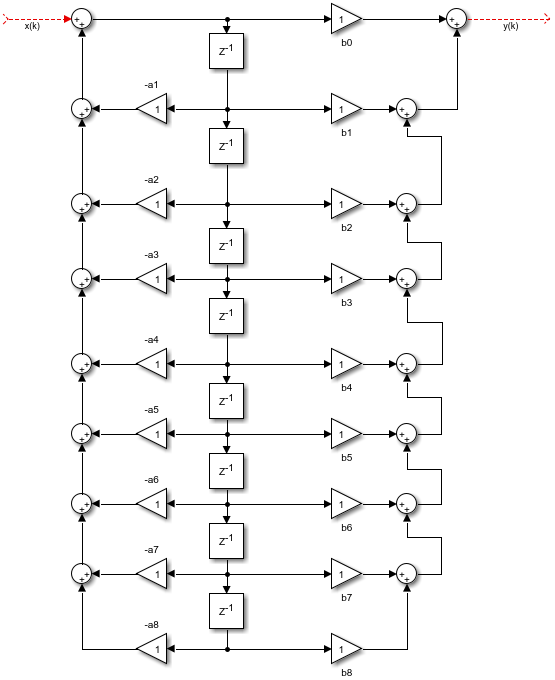 Рисунок 1. Структурная схема Частота дискретизация выбрана в 2 раза больше, чем частота среза , 200 Гц. 2. Пояснить порядок работы схемы фильтра. Задержка дискретной последовательности на один такт – это произведение z на z-1 (свойства z-преобразования). На структурной схеме такие элементы обозначаются как z-1. Порядок фильтра – это количество предыдущих отсчетов в схеме. Предыдущие отсчеты сигнала хранятся в ячейках памяти, образующие дискретную линию задержки. Эти отсчеты умножаются на коэффициенты bk и ak и суммируются, формируя выходной отсчет y(n). 3. Найти аналитическое выражение для амплитудно-частотной характеристики фильтра A(f ) и построить её график. Нахождение аналитического выражения и построение графика АЧХ выполнено в программе Matlab clear, clc N = 7; % Порядок фильтра fc = 1000; % Частота среза fs = 2000; % Частота дискретизации, выбрана как fc*2, частота Найквиста Rp = 0.01; % Неравномерность в полосе пропускания % Rs = 30; % Уровень подавления в полосе заграждения wp = pi*fc/fs; % Нормированная частота среза T = 2; % Интервал дискретизации syms s z w; % Символьные переменные Wp = tan(wp/2); % Расчет частоты среза аналогового фильтра eps_p = sqrt(power(10, Rp/10)-1); % eps_s = sqrt(power(10, Rs/10)-1); % Ws = power(10, log(eps_s/eps_p)/N)*Wp L = floor(N/2); r = N-2*L; alpha = 1/(power(eps_p, 1/N)) alpha = 1.5430 % Расчет передаточной характеристики аналогового нормированного ФВЧ % Цикл расчета произведения prod = 1; for i = 1:L teta = (2*i-1)/(2*N)*pi; prod = prod*(s^2+2*alpha*sin(teta)*s+alpha^2); end Hh(s) = 1/(eps_p*(s+alpha)^r*prod); % Передаточная характеристика нормированного ФВЧ vpa(Hh(s), 2) ans = % Частотное преобразование передаточной характеристики аналогового нормированного ФВЧ Hh1(s) = Hh(Wp/s); vpa(Hh1(s), 2) ans = 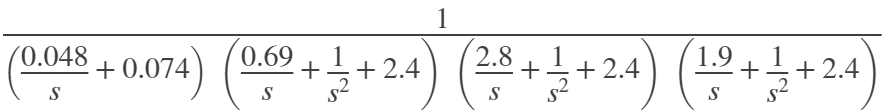 % Расчет передаточной характеристики цифрового фильтра Hh2(z) = Hh1((2/T)*(1-z^-1)/(1+z^-1)); % Билинейное преобразование vpa(Hh2(z), 2) ans = 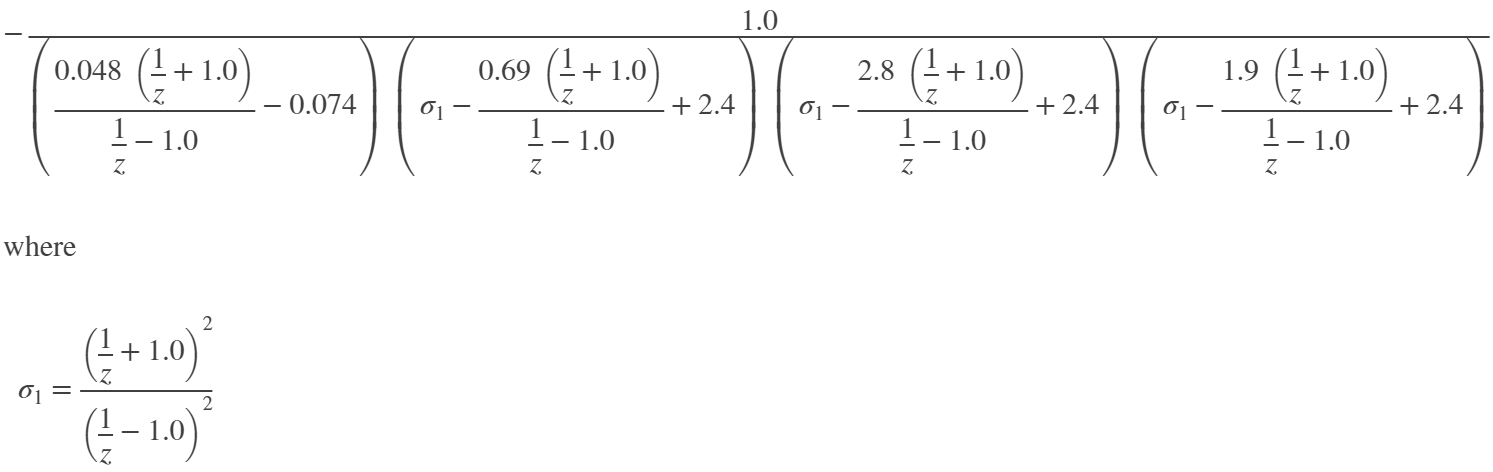 % Расчет АЧХ фильтра w = 0.01:0.01:pi; fq = double(abs(Hh2(exp(1i*w))).^2); f = fs/length(w):fs/length(w):fs; figure plot(f, fq) title('График АЧХ') xlabel('Частота, Гц') ylabel('Коэффициент усиления') 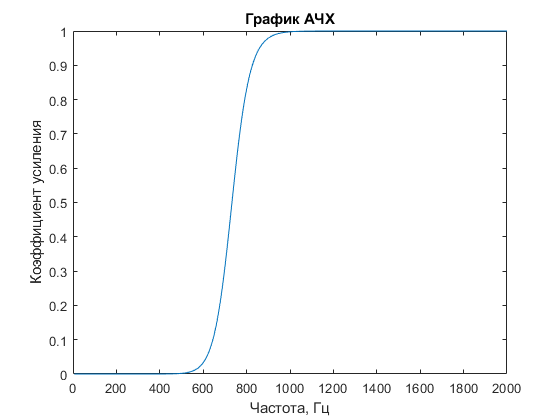 |
