Надежность и долговечность зданий и сооружений. Методы расчета и прогнозирования
 Скачать 55.38 Kb. Скачать 55.38 Kb.
|
|
Министерство науки и высшего образования РФ Казанский государственный архитектурно-строительный университет Кафедра строительных материалов РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА по дисциплине «Надежность и долговечность зданий и сооружений. Методы расчета и прогнозирования» Выполнил: ст-т гр. № 9СМ01 Руководитель: д.т.н. Сулейманов А.М. Казань, 2020 г. ЗАДАНИЕна расчетно-графическую работу по дисциплине «Надежность и долговечность зданий и сооружений. Методы расчета и прогнозирования» Студенту группы 9СМ01 Куппер М. 1.Определить коэффициенты уравнения Журкова (τ0, U0, γ) для конструкционного материала из алюминия если известны экспериментальные значения зависимости τ(σ,Т) (Таблицы 1-4); 2. Определить эквивалентную температуру эксплуатации Тэ в уравнении Журкова если известны статистические данные воздействия температур (Таблица 5); Таблица 1 зависимости τ(σ) при Т = 180 С
Таблица 2 зависимости τ(σ) при Т = 1000 С
Таблица 3 зависимости τ(σ) при Т = 2000 С
Таблица 4 зависимости τ(σ) при Т = 3000 С
Таблица 5 3. В теоретической части привести следующие сведения: - теория Гриффитса для хрупкого разрушения; - кинетическая природа прочности твердых тел; - статистическая природа прочности твердых тел; - усталостная прочность материалов. СодержаниеЗАДАНИЕ 2 Введение 5 Теория Гриффитса для хрупкого разрушения 7 Кинетическая природа прочности твердых тел 8 Усталостная прочность материалов 8 Расчетная часть 9 Задача 1 9 Задача 2 12 Заключение 13 Используемая литература 15 ВведениеУже много столетий человек задается вопросом о прочности и разрушении предметов и тел, окружающих его. На протяжении долгих лет люди сталкиваются с проблемой прочности в ходе строительства зданий и сооружений. В ходе развития истории и попыток решения вышеуказанной проблемы происходили аварии и разрешения, из которых люди выносили урок, они изучали печальный опыт прошлых лет и совершенствовали свои навыки по проектированию. Долговечность – это способность здания и строительных конструкций сохранять во времени свои эксплуатационные качества до наступления предельного состояния при условии проведения своевременного технического обслуживания и ремонта. Показателем долговечности является средний срок службы до первого капитального ремонта. Долговечность сооружений в свою очередь зависит от долговечности строительных материалов, из которых изготовлены их конструктивные элементы. Надежность характеризуется способностью здания и отдельных ее строительных конструкций выполнять свои эксплуатационные качества в заданных пределах, в течение требуемого промежутка времени. Она базируется на долговечности и безотказности работы, как строительных конструкций, так и всего здания в целом. Надежность здания ассоциируется у человека с прочностью, причем не отдельных ее систем, а в целом объекта. В проекте, при расчетах, закладывается теоретическая прочность каждой строительной конструкции. После изготовления и строительства получаем фактическую прочность. Определение теоретической надежности требует учета: количеств и качества используемых строительных конструкций и их элементов; режима и условий эксплуатации; условий стандартизации и унификации; возможности замены или ремонта отдельных конструкций и элементов. В реальных условиях изготовления, монтажа строительных конструкций возможны нарушения правил монтажа, низкое качество материалов и работ, низкий контроль на операциях при возведении, что существенно снижает долговечность и надежность. Вместе с тем к дефектам, полученным в процессе возведения, добавляются внутренние и местные напряжения, не учтенные внешние воздействия, неграмотная или неквалифицированная эксплуатация обслуживающего персонала. Вопросы качества и долговечности строительных конструкций как в техническом, так и в экономическом аспекте привлекают все большее внимание строителей. Очевидно, что во многих случаях экономически оправдано увеличение первоначальных затрат на изготовление конструкции и ее надежную защиту, если это позволяет сократить число и стоимость ремонтов в процессе эксплуатации. В связи с этими условиями определение долговечности является ключевым моментом в проектировании зданий. Поэтому следует выделить теорию Журкова – как один из самых распространненых способов определения долговечности конструкций. Теория Гриффитса для хрупкого разрушенияКинетическая природа прочности твердых телУсталостная прочность материаловРасчетная частьЗадача 1В задании 1 нам необходимо определить коэффициенты уравнения Журкова (τ0, U0, γ) для конструкционного материала из алюминия если известны экспериментальные значения зависимости τ(σ,Т) (Таблицы 1-4):
Для температуры равной Т1=18оС.
Для температуры равной Т2=100оС.
Для температуры равной Т3=200оС.
Для температуры равной Т4=200оС. Прочность различных материалов имеет линейную природу, зависит не только от величины, но и продолжительности воздействия механической нагрузки. Исходя из данных, приведенных в таблицах 1-4, построим графики. Эта прочность – длительная прочность (рис.1.) длительная прочность и механическая нагрузка находятся в линейной зависимости. 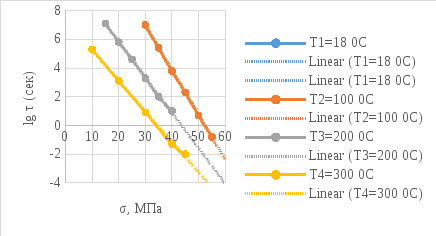 Рис. 1 Веер прямых в координатах (lg τ) – (σ) Как видно из рис.1 линейная зависимость сохраняется при различных температурах. В этой зависимости при увеличении температуры меняется лишь наклон прямой. Если эти прямые экстраполировать к оси (σ), то они будут сходиться в одной точке (полюсе). Эта точка для всех твердых тел лежит при практически одном и том же значении долговечности 10-13. Измерение долговечности при разных температурах позволяет определить температурную зависимость долговечности твердого тела при фиксированных разрывных напряжениях. Для этого необходимо измеренное значение lg τ наносить на график в зависимости от обратной абсолютной температуры t=1/T, [К] (рис.2). Т1=18+273=291К; Т2=100+273=373К; Т3=200+273=473К; Т4=300+273=573К. (1/Т1)х100=(1/291)х1000=3,43; (1/Т2)х100=(1/373)х1000=2,68; (1/Т3)х100=(1/473)х1000=2,11; (1/Т4)х100=(1/573)х1000=1,75. 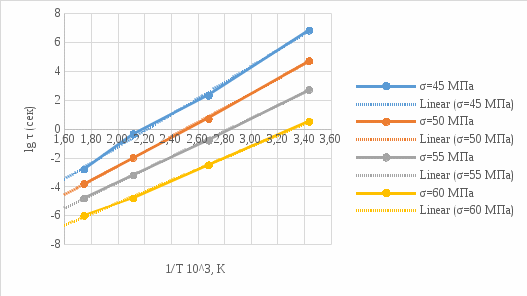 Рис.2 Веер прямых (lg τ) – (1/T) Как видно из рис.2. зависимость (lg τ) – (1/T) при различных σ с достаточной точностью оказывается линейной, при этом прямые образуют «температурный веер» с полюсом, лежащим на оси ординат. Значение U для различных σ, т.е. Uσ может быть определено из наклона прямых на графике рис.2 (lg τ) – (1/T) по формуле: 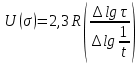 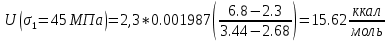 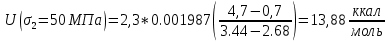 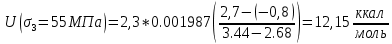 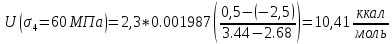 Uσ – энергия активации разрушения. Далее стоим график (Uσ) – (σ) рис.3. Экстраполируя к σ0, получаем U0 – энергия активации, [ккал/моль], а по наклону прямой определяем γ: γ =αRT 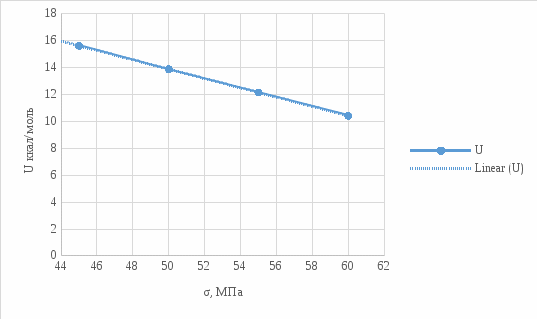 Рис.3 По графику рис.3 видно, что сам график пересекается с осью U в точке равное U0 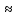 31,24 ккал/моль и γ=arct(5.2/15)=20.72⁰ 31,24 ккал/моль и γ=arct(5.2/15)=20.72⁰Коэффициент τ0 находится из положения полюса, в которой при экстраполяции сходится веер прямых в координатах (lg τ) – (σ) (рис.1) или (lg τ) – (1/T) (рис.2). Исходя из рис.1, можно сделать вывод о том, что пересечение графиков происходит в точке lg τ = -13, таким образом τ0= 10-13, сек. Таким образом, решением поставленной задачи является: τ0 = 10-13 U0 = 31,24 ккал/моль γ = 20,72⁰. Задача 2В задаче 2 нам необходимо определить эквивалентную температуру эксплуатации Тэ в уравнении Журкова если известны статистические данные воздействия температур (Таблица 5); Таблица 5
Для нахождения эквивалентной температуры эксплуатации необходимо воспользоваться формулой: 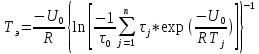 , ,где U0 – энергия активации, [Дж/моль] (ккал/моль); R – Универсальная газовая постоянная, [Дж/моль х К]; τ0 – период (время) эксплуатации, (час) или (условный год). Δ τj – продолжительность существования интервала температур (не более 5о) со средней температурой τj; n – количество интервалов температур со средней температурой τj. τ0=16+27+140+490+1059+1193+1060+1022+1190+1344+793+390+43=9867 ч. Из предыдущей задачи знаем, что U0 = 31,24 ккал/моль. Для удобства расчета данное выражение рассчитаем этапами: 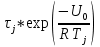 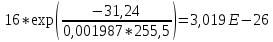 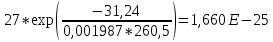 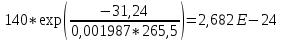 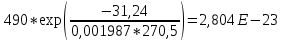 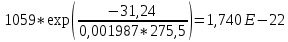 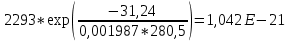  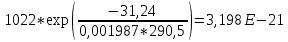 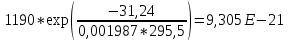 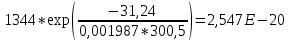 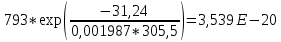 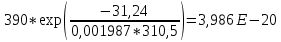 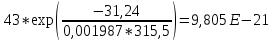 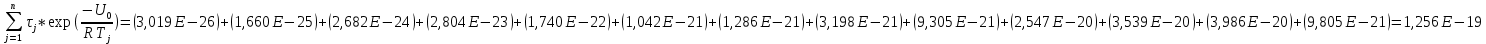 Теперь по формуле вычисляем эквивалентную температуру эксплуатации: 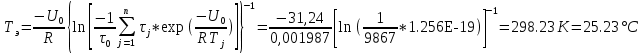 Таким образом, решением поставленной задачи является: Тэ=298,23К=25,23оС. ЗаключениеПрогнозирование долговечности строительных конструкций России является важной проблемой, которая неразрывно связана с улучшением использования основных фондов и экономией материально-технических ресурсов. Качество и долговечность строительных конструкций сокращают число ремонтов в течение срока службы здания или сооружения. Здания и инженерные сооружения возводятся из строительных материалов. Каждый строительный материал обладает рядом присущих ему свойств. Одни материалы придают прочность, несущую способность и жесткость конструкциям и сооружениям в целом. Другие материалы предназначены для облицовки внутренних и наружных стен, придания архитектурного облика сооружениям. Материалы в сооружении подвергаются воздействию окружающей среды, которая оказывает на них разрушающее действие. Поэтому сделать правильный их выбор, уметь оценить их качество и обеспечить нормальные условия эксплуатации конструкций из этих материалов – все это необходимо строителям любой специальности. В соответствии с этим каждый материал, кроме выполнения эксплуатационных функций, должен обладать свойствами, обеспечивающими надежность и долговечность сооружения. Надежность и долговечность материалов и конструкций при эксплуатации зданий и сооружений – важная научно-техническая проблема. Решение ее связано с изучением причин и механизмов разрушения материалов, поиском надежных способов предупреждения и защиты от разрушения отдельных элементов зданий и сооружений. Используемая литература1) Николаева Е.А. Основы механики разрушения. Издательство Пермского государственного технического университета, 2010. 103с. 2) Регель В. Р., Слуцкер А. И., Томашевский Э. И. Кинетическая природа прочности твердых тел.М.: Наука, 1974. 3) Ратнер С. Б., Ярцев В. П. Физическая механика пластмасс. Как прогнозируют работоспособность М.: Изд-во «Химия», 1992. 320 с 4) Ярцев В. П. Прогнозирование работоспособности полимерных материалов в деталях и конструкциях зданий и сооружений: Учеб. пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2001. 149 с. 6) ГОСТ 9.707-81 (Приложение 5). 7) Вахромеев А.М. Определение циклической долговечности материалов и конструкций транспортных средств: методические указания /А.М. Вахромеев. – М.: МАДИ, 2015. – 64 с. 8) Когаев, В.П. Расчет на прочность при напряжениях, переменных во времени / В.П. Когаев. – М.: Машиностроение, 1993. – 354 с. 9) ГОСТ 33845-2016 Композиты полимерные. Метод определения характеристик усталости в условиях циклического Нагружения. |

