Надежность 4 вариант. Вариант 4. надежность и эффективность экономических информационных систем

• Название: надежность и эффективность экономических информационных систем
• Анкор: Надежность 4 вариант
• Дата: 03.11.2021
• Размер: 128.77 Kb.
• Имя файла: Вариант 4.docx
• Тип: Документы; #262161

Тверской государственный технический университет,

факультет информационных технологий

Кафедра информационных систем

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА

по дисциплине

«НАДЕЖНОСТЬ И ЭФФЕКТИВНОСТЬ ЭКОНОМИЧЕСКИХ ИНФОРМАЦИОННЫХ СИСТЕМ»

Тверь, 2021


По структурной схеме надежности технической системы в соответствии с вариантом задания , требуемому значению вероятности безотказной работы системы γ и значениям интенсивностей отказов ее элементов γ , требуется:

1. 
   Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1-0.2.
   
2. 
   Определить γ-процентную наработку технической системы.
   
3. 
   Обеспечить увеличение γ-процентной наработки не менее ,чем в 1,5 раза за счет :
   

А) повышения надежности элементов;

В) структурного резервирования элементов системы.

Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов) Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов .Переключатели при резервировании считаются идеальными.

На схемах обведенные пунктиром m элементов являются функционально необходимыми из n параллельных ветвей.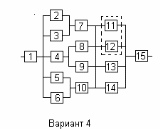

Рис.1 Исходная схема

1. В исходной схеме элементы: 2,3 образуют параллельное соединение. Заменяем их элементом А. Учитывая ,что p₂=p₃ получим:
p_A=1-q₂q₃ = 1- q₂² =1-(1-p₂ )² (1)

2. Элементы: 5,6 образуют параллельное соединение. Заменяем их элементом B. Учитывая ,что p₅=p₆ получим:
p_B=1-q₅q₆ = 1- q₅² = 1-(1-p₅ )² (2)

3. 
   Элементы: 8,9 образуют параллельное соединение. Заменяем их элементом C. Учитывая ,что p₈=p₉ получим:
   

P_C=1-q₈q₉= 1- q₈⁴ = 1-(1-p₈ )² (3)

4. Элементы 11 , 12 , 13 и 14 образуют соединение “2 из 4”, которое заменяем элементом E. Так как 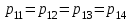, то для определения вероятности безотказной работы элемента E можно воспользоваться комбинаторным методом: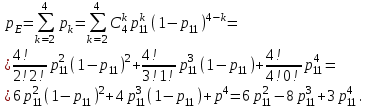

(4)

Преобразованная схема изображена на 2 рис.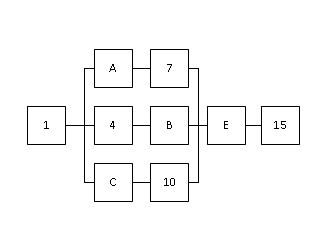



Рис. 2 Преобразованная схема

5. 
   В исходной схеме элементы: А,7 образуют последовательно соединение. Заменяем их элементом F.
   

P_F=P_A*P₇ (5)

5. 
   В исходной схеме элементы: 4,B образуют последовательно соединение. Заменяем их элементом G.
   

P_G=P₄*P_B (6)

5. 
   В исходной схеме элементы: C,10 образуют последовательно соединение. Заменяем их элементом I.
   

P_I=P_C*P₁₀ (7)

5. 
   В исходной схеме элементы: E,15 образуют последовательно соединение. Заменяем их элементом J.
   

P_J=P_E*P₁₅ (8)
Преобразованная схема изображена на 3 рис.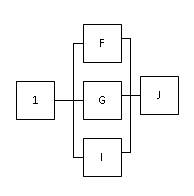



Рис. 3 Преобразованная схема

5. 
   Элементы: F,G и I образуют параллельное соединение. Заменяем их элементом K. Учитывая ,что p_F = p_G = p_I получим:
   

P_K=1-q_Fq_Gq_I = 1- q_F³ = 1-(1-p_F)³ (9)
Преобразованная схема изображена на 4 рис.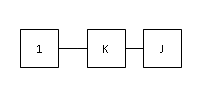



Рис. 4 Преобразованная схема
9. В преобразованной схеме элементы 1, K, J образуют последовательное соединение. Тогда вероятность безотказной работы всей системы определяется выражением:

P=p1*pK*pJ (10)

10. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 подчиняются экспоненциальному закону: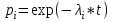

(11)
11. Результаты расчетов вероятностей безотказной работы элементов 1 - 15 исходной схемы по формуле (11) для наработки до 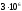часов представлены в таблице 1.
12. Результаты расчетов вероятностей безотказной работы квазиэлементов A, B, C, E, F, G, I, J и K по формулам (1) - (8) и (9) также представлены в таблице 1.

Таблица 1

Расчет вероятности безотказной работы системы

элемент	λ1, 10^-6	Наработка t, 10^6
		0,5	1	1,5	2	2,5	3	1,9	2,85
1	0,001	0,9995	0,9990	0,9985	0,9980	0,9975	0,9970	0,9981	0,9972
2-3	0,1	0,9512	0,9048	0,8607	0,8187	0,7788	0,7408	0,8270	0,7520
4	0,15	0,9277	0,8607	0,7985	0,7408	0,6873	0,6376	0,7520	0,6521
5-6	0,01	0,9950	0,9900	0,9851	0,9802	0,9753	0,9704	0,9812	0,9719
7	0,16	0,9231	0,8521	0,7866	0,7261	0,6703	0,6188	0,7379	0,6338
8-9	0,2	0,9048	0,8187	0,7408	0,6703	0,6065	0,5488	0,6839	0,5655
10	0,25	0,8825	0,7788	0,6873	0,6065	0,5353	0,4724	0,6219	0,4904
11-14	0,5	0,7788	0,6065	0,4724	0,3679	0,2865	0,2231	0,3867	0,2405
15	0,55	0,7596	0,5769	0,4382	0,3329	0,2528	0,1920	0,3517	0,2086
A		0,9976	0,9909	0,9806	0,9671	0,9511	0,9328	0,9701	0,9385
B		1,0000	0,9999	0,9998	0,9996	0,9994	0,9991	0,9996	0,9992
C		0,9909	0,9671	0,9328	0,8913	0,8452	0,7964	0,9001	0,8112
E		0,9639	0,8282	0,6449	0,4687	0,3246	0,2173	0,5018	0,2458
F		0,9209	0,8444	0,7714	0,7023	0,6375	0,5772	0,7158	0,5948
G		0,9277	0,8606	0,7983	0,7405	0,6869	0,6371	0,7517	0,6516
I		0,8745	0,7532	0,6411	0,5406	0,4524	0,3762	0,5597	0,3978
J		0,7321	0,4779	0,2826	0,1560	0,0821	0,0417	0,1765	0,0513
K		0,9995	0,9962	0,9880	0,9736	0,9524	0,9244	0,9770	0,9335
P		0,7314	0,4756	0,2788	0,1516	0,0780	0,0385	0,1721	0,0477
15'	0,332	0,8470	0,7175	0,6077	0,5148	0,4360	0,3694	0,5322	0,3882
J'		0,816459	0,594253	0,391964	0,241262	0,141534	0,080256	0,267025	0,095426
P'		0,8156	0,5914	0,3867	0,2344	0,1345	0,0740	0,2604	0,0888
16	0,315	0,8543	0,7298	0,6234	0,5326	0,4550	0,3887	0,5496	0,4075
J''		0,8234	0,9371	0,8467	0,7347	0,6171	0,5052	0,7580	0,5377
P''		0,70274	0,680612	0,520802	0,380224	0,26674	0,18096	0,4063	0,203947

13. На рис. 5 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.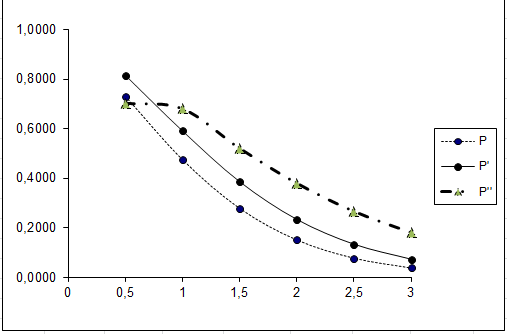


Рис 5. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`) и системы со структурным резервированием элементов (Р``).

14. По графику (рис. 5, кривая P) находим для - процентную наработку системы ч.

15. Проверочный расчет при ч показывает (таблица 1), что .

16. По условиям задания повышенная - процентная наработка системы ч.

17. Расчет показывает (таблица 1), что при ч для элементов преобразованной схемы (рис.5) и . Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент J и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.

18. Для того, чтобы при ч система в целом имела вероятность безотказной работы , необходимо, чтобы элемент J имел вероятность безотказной работы (см. формулу (10))

(12)

При этом значении элемент J останется самым ненадежным в схеме (рис. 5) и рассуждения останутся верными.

Очевидно, значение p_J, полученное по формуле (8), является минимальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях увеличение надежности системы будет большим.

19. Для определения минимально необходимой вероятности безотказной работы элемента 15 (рис..1) необходимо решить уравнение (4) относительно p₁₅ при p_J = 0.5371. Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями, более целесообразно использовать графо-аналитический метод. Для этого по данным табл. 7.1 строим график зависимости p_J = f(p₁₅). График представлен на рис. 6.


Рис. 6. Зависимость вероятности безотказной работы системы K от вероятности безотказной работы ее элементов
20. По графику при p_J = 0. 5371 находим .

21. Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (8), то для элемента 15 при находим

ч . (13)

22. Таким образом, для увеличения - процентной наработки системы необходимо увеличить надежность элемента 15 и снизить интенсивность его отказов с до ч , т.е. в 3 раза.

23. Результаты расчетов для системы с увеличенной надежностью элемента 15 приведены в таблице 1. Там же приведены расчетные значения вероятности безотказной работы системы E` и системы в целом P`. При ч вероятность безотказной работы системы , что соответствует условиям задания. График приведен на рис 5.

24. Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования - по тем же соображениям также выбираем элемент J, вероятность безотказной работы которого после резервирования должна быть не ниже .

25. Для элемента J - резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция дискретна.

26. Для повышения надежности системы добавляем к ней элементы, идентичные по надежности исходным элементу 15, до тех пор, пока вероятность безотказной работы квазиэлемента J не достигнет заданного значения.

Для расчета воспользуемся комбинаторным методом:

- добавляем элемент 16:

P_J=P_E*P₁₅*P₁₆ = 0.5377 > 0.5371
27. Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис.1) достроить элементами 16 до системы (рис. 7).



Рис. 7 Структурная схема системы после структурного резервирования
28. Результаты расчетов вероятностей безотказной работы системы J`` и системы в целом P`` представлены в таблице 1.

29. Расчеты показывают, что при ч , что соответствует условию задания.

30. На рис. 5 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элемента 15 (кривая ) и после структурного резервирования (кривая ).
Выводы:

1. На рис. 5 представлена зависимость вероятности безотказной работы системы (кривая ). Из графика видно, что 50% - наработка исходной системы составляет часов.

2. Для повышения надежности и увеличения 50% - наработки системы в 3 раза (до часов) предложены два способа:

а) повышение надежности элемента 15 и уменьшение его отказов с до ч ;

б) нагруженное резервирование основного элемента 15 идентичными по надежности резервными элементами 16 (6).

3. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис. 5) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до часов вероятность безотказной работы системы при структурном резервировании (кривая ) выше, чем при увеличении надежности элементов (кривая ).