Нахождение доверительного интервала для оценивания неизвестных параметров статистического распределения
 Скачать 54.5 Kb.
|
|
Тема №13.Доверительные интервалы Цель занятия: 1) Проверить умения студентов применять знания по пройденным темам. Содержание занятия: Нахождение доверительного интервала для оценивания неизвестных параметров статистического распределения Задача 1. Найти доверительный интервал для оценки с надежностью P=0,95 неизвестного математического ожидания A нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение S=5, выборочная средняя  , а объем выборки N=25.Решение.Интервальной оценкой называется интервал, покрывающий оцениваемый параметр. Доверительным интервалом является интервал, который с данной надежностью покрывает оцениваемый параметр. Для оценки математического ожидания A нормально распределенного количественного признака Х по выборочной средней  при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал ,Где  – точность оценки, T – значение аргумента функции Лапласа  (приложение, таблица 2).В данной задаче T находим из условия  . По приложению 2 определяем  . Таким образом, T=1,96.Далее получаем  Или  Задача 2. По данным N=9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений  и исправленное среднее квадратическое отклонение S=6. Оценить истинное значение измеряемой величины при помощи доверительного интервала с надежностью  =0,99.Решение. Оценкой математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения является доверительный интервал  .По приложению 3 приложения, по заданным N и  находим  =3,36.Таким образом  Окончательно получаем  Задача 3. Из генеральной совокупности извлечена выборка объема N. Оценить с надежностью =0,95 математическое ожидание A нормально распределенного признака Х генеральной совокупности по выборочной средней с помощью доверительного интервала.
Решение. Объем данной выборки равен   По данным задачи находим выборочную среднюю: 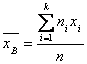  Далее находим исправленное среднее квадратическое отклонение S: 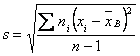  Для оценки математического ожидания A нормально распределенного количественного признака Х в случае неизвестного среднего квадратического отклонения служит доверительный интервал .По приложению 3 приложения по заданным N и находим =2,26.Таким образом  Окончательно получаем  Основные вопросы: Задание для самостоятельной работы:№№ 6-7 стр 247-248/4/ Методические рекомендации к выполнению задания: Решение задач и примеров следует излагать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Решение каждой задачи должно доводится до окончательного ответа, которого требует условие. В промежуточные вычисления не следует вводить приближенные значения корней, числа π и т.п. Полученный ответ следует проверить способами, вытекающими из существа данной задачи. Форма отчетностиписьменно |