Найдем сколькими способами можно вычеркнуть 3 строки из 5
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
 Найдем сколькими способами можно вычеркнуть 3 строки из 5: 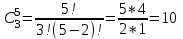 способов способовНайдем сколькими способами можно вычеркнуть 3 столбца из 4: 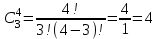 способа способаТогда найдем сколькими способами можно вычеркнуть в матрице 5*4 3 строки и 3 столбца: 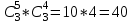 способами способами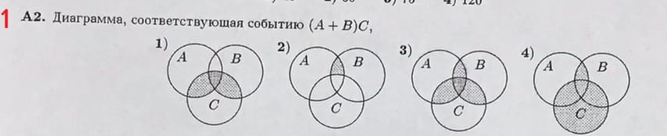 Можно записать как: 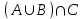 Найдем А 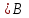 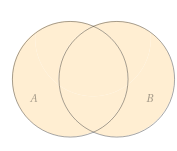 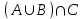   Число элементарных исходов равно числу размещений 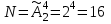  Трехзначные цифры это от 100 до 999, тогда n=900 На первом месте трехзначного числа можно записать любую из четырех четных цифр 2, 4, 6, 8, а на втором— любую из пяти четных цифр 0,2,4,6,8 Всего способов записи трехзначного числа у которого на первом и втором месте четная цифра: m=4*25=100 способов Получаем: Р=m/n=100/900=1/9  Так как площадь вписанного в окружность с радиусом R квадрата Sk равна 2R2=2 , а площадь окружности So равна πR2=π , то, следовательно, вероятность попадания точки в этот квадрата P будет: P= 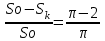  По формуле вероятности суммы двух независимых событий: Р(А+В)=Р(А)+Р(В)-Р(АВ)=0,9+0,7-(0,9*0,7)=0,97  После перекладывания карты в колоде станет 37 карт. Вероятность выпадения каждой масти равна 1/4 Введём две гипотезы: - вытащенная карта изначально была во второй колоде, 36/37; - вытащенная карта была переложена из первой колоды, 1/37. Случайное событие А - вытащенная карта бубни. По формуле полной вероятности находим Р(А)= 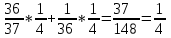  По условию, для этого остаточно 2 или 3 попадания. Эти события несовместны, поэтому вероятность разрушения объекта равна сумме вероятностей. q=2/3, p=1/3 Р=Р3(2)+Р3(3) Однако проще сначала найти вероятность противоположного события (ни одного попадания или одно попадание) 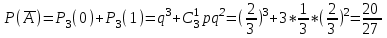 P(A)=1-20/27=7/27  Так как вероятность сдачи с первой попытки равна p=0,75, q=1-0,75=0,25 Тогда вероятность, что студент сдаст со второй попытки P=(1-0,75)*0,6=0,15 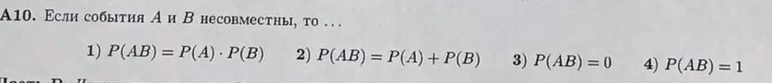 Если события A и B несовместны, то вероятность их произведения равна нулю. Другими словами, для несовместных событий A и B верна формула Если события A и B несовместны, то вероятность суммы событий A + B равна сумме вероятностей событий A и B . Другими словами, для несовместных событий A и B верна формула P (A + B) = P (A) + P (B) Скорее здесь ответ 3 чем 2  Вероятность выпадения герба равна ½, и цифры 1/2 Для первого случая : Р= 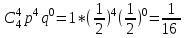 Для второго случая: Р= 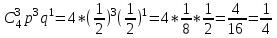 Для третьего случая: Р= 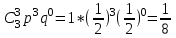 Для четвертого случая Р= 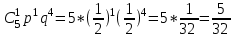  Воспользуемся интегральной теоремой Лапласа: Pn(k1,k2) = Ф(x2) – Ф(x1) где Ф(x) – функция Лапласа. 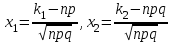 k2 = 302, k1 = 284 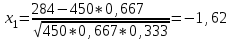 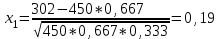 Учитывая, что функция Лапласа нечетная, т.е. Ф(-x) = -Ф(x), получим: P450(284 < x < 302) = Ф(0.19) - Ф(-1.62) = 0.0753 - (-0.4474) = 0.5227 |
