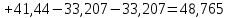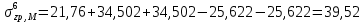механика грунтов. С.В.В._Механика грунтов_Практическая работа 3_. Напряжения в грунтах от действия внешних сил
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» Архитектурно-строительный институт (наименование института полностью) Центр Архитектурных, конструктивных решений и организации строительства (наименование кафедры/департамента/центра полностью) 08.03.01 Строительство (код и наименование направления подготовки, специальности) «Промышленное и гражданское строительство» (направленность (профиль) / специализация) Практическое задание №_3_ по учебному курсу «Механика грунтов» (наименование учебного курса) Вариант 17
Тольятти 2021 Тема «Напряжения в грунтах от действия внешних сил» Исходные данные Горизонтальная поверхность массива грунта нагружена равномерно распределенной вертикальной нагрузкой интенсивностью р1 и р2. Размеры прямоугольных площадок в плане: l1 х b1 и l2 х b2. Необходимо определить величины вертикальных напряжений σzp от совместного действия распределенных нагрузок на поверхности в грунтовой толще на вертикали, проходящей через точку M, на глубинах 1,0; 2,0; 3,0; 4,0; 5,0; 6,0 м. Расстояние между осями площадок нагружения – L = 3,0 м. По вычисленным напряжениям построить эпюру распределения σzp.
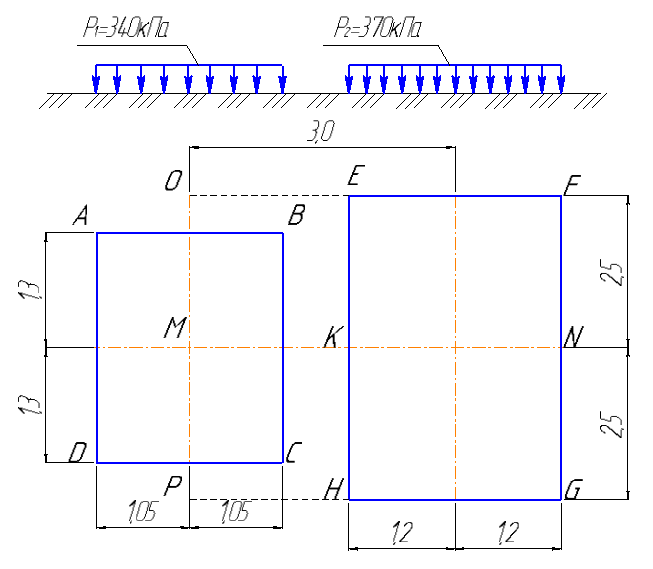 Рисунок 3.2 – Расчетная схема к заданию 3 (пример) Расчет напряжений и построение эпюры Распределение по глубине вертикальных составляющих напряжений σzp в любой точке массива грунта от действия равномерно распределенной нагрузки в пределах или за пределами плит нагружения может быть определено по методу угловых точек. Метод угловых точек применяется тогда, когда грузовая площадь может быть разбита на отдельные прямоугольники, в которых точка, соответствующая оси, является угловой. Максимальное сжимающее напряжение для площадок под центром загружения прямоугольника определяется по формуле: 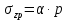 , (3.1) , (3.1)где α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения 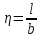 (l – длинная сторона, b – меньшая сторона независимо от направления сторон, l > b) и относительной глубины (l – длинная сторона, b – меньшая сторона независимо от направления сторон, l > b) и относительной глубины 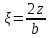 (z – глубина, на которой определяется напряжение); (z – глубина, на которой определяется напряжение);p – интенсивность равномерно распределенной нагрузки. Вертикальные напряжения по вертикали, проходящей через угловую точку загруженного прямоугольника, определяются по формуле: 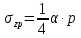 , (3.2) , (3.2)где α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения 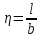 (l – длинная сторона, b – короткая сторона независимо от направления сторон, l > b) и относительной глубины (l – длинная сторона, b – короткая сторона независимо от направления сторон, l > b) и относительной глубины 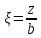 (z – глубина, на которой определяется напряжение); (z – глубина, на которой определяется напряжение);p – интенсивность равномерно распределенной нагрузки. Значения коэффициента α приведены в таблице В.1 приложения В. В соответствии с этим плиты разбивают на прямоугольники таким образом, чтобы они имели общую угловую точку M. Вводятся размеры соответствующих получившихся прямоугольников:
Искомые напряжения в точке М от действия нагрузки по прямоугольникам 1, 2 и 3, взятые со знаком «+», прямоугольникам 4 и 5 со знаком «−», определяются по формуле: 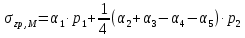 (3.3) (3.3)Вычисления вносим в табличной форме. Напряжения в точке № 1 (на глубине 1 м)
Напряжения в точке № 2 (на глубине 2 м)
Напряжения в точке № 3 (на глубине 3 м)
Напряжения в точке № 4 (на глубине 4 м)
Напряжения в точке № 5 (на глубине 5 м)
Напряжения в точке № 6 (на глубине 6 м)
Эпюра напряжений строится по полученным значениям, как показано на рисунке 3.3. Масштаб расстояний – 1:50, масштаб напряжений – 50 кПа в 1 см. 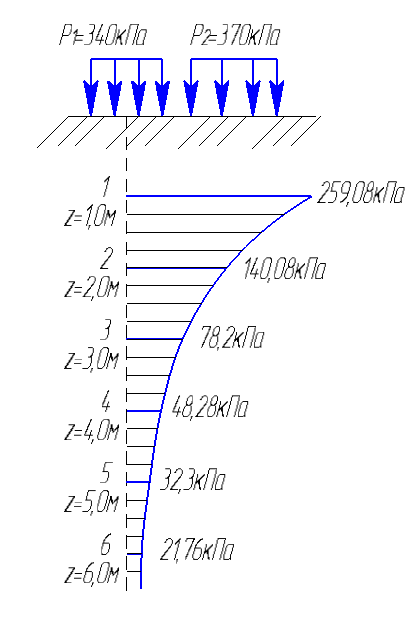 Рисунок 3.3 – Эпюра распределений вертикальных напряжений σzp Приложение В Таблица В.1 – Значения коэффициента α (СП 22.13330.2016)
Примечание Для промежуточных значений ξ и η коэффициенты α определяют интерполяцией. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

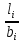
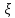
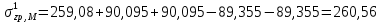
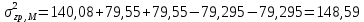
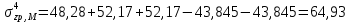
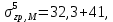 44
44