|
|
Ханикалов_Теоремыс. Некоторые теоремы разрешимости нелинейных уравнений второго рода и их приложения к уравнениям с сингулярными интегралами
Некоторые теоремы разрешимости нелинейных уравнений второго рода и их приложения к уравнениям с сингулярными интегралами
Х.Б. Ханикалов
ДГУ, Махачкала
УДК 517.946
Аннотация: В статье исследуются нелинейные уравнения второго рода с сингулярными интегралами в комплексных пространствах  . Приведены теоремы разрешимости этих уравнений. . Приведены теоремы разрешимости этих уравнений.
Ключевые слова: оператор, монотонность, коэрцитивность, нелокальная
разрешимость, пространства.
Рассматриваются общие уравнения и системы типа


в действительных и комплексных пространствах  . .
Всюду в работе  - линейный вектор-оператор, вектор - оператор - линейный вектор-оператор, вектор - оператор  - известный оператор суперпозиции, называемый оператором Немыцкого, - известный оператор суперпозиции, называемый оператором Немыцкого,  - в общем случае вектор-функция. - в общем случае вектор-функция.
В наших приложениях А – линейный сингулярный интегральный оператор и он не может быть компактным и не действует в L1. Мы нигде в работе от Fu не требуем малоконструктивного для систем условия монотонной (секторной) ограниченности оператора F.
Полученные общие результаты для уравнений (I) и (II) перенесены на случай когда А – линейный сингулярный интегральный оператор, а оператор F действует из Lp в Lq. Частично результаты анонсированы ранее в работах [5]- [7].
1. Общие теоремы существования и единственности
Всюду в работе 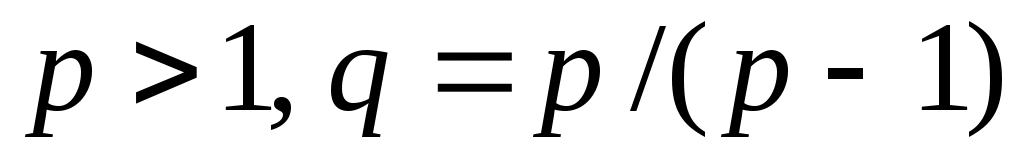 , ,
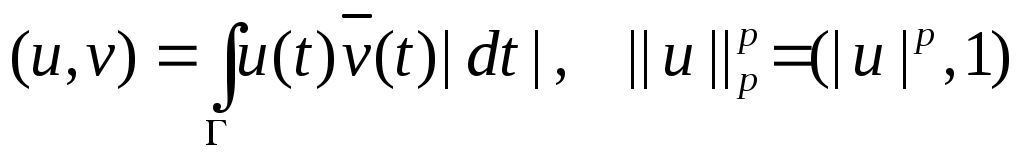 , ,
 - гладкая линия на комплексной плоскости С. Функция - гладкая линия на комплексной плоскости С. Функция   С С С С измерима на контуре измерима на контуре 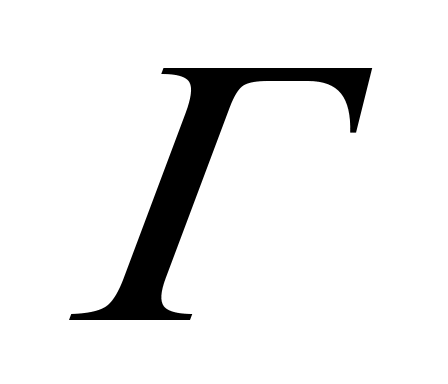 при каждом при каждом  C и непрерывна по C и непрерывна по  при каждом при каждом  . .
Функция  называется монотонной по называется монотонной по  почти при каждом почти при каждом  , если , если
 . .
Всюду в работе  - монотонная функция в комплексном С. - монотонная функция в комплексном С.
Теорема 1.1. Пусть функция  удовлетворяет неравенству удовлетворяет неравенству
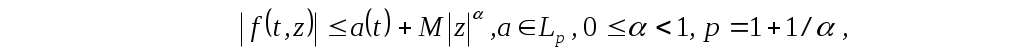 (1) (1)
линейный оператор 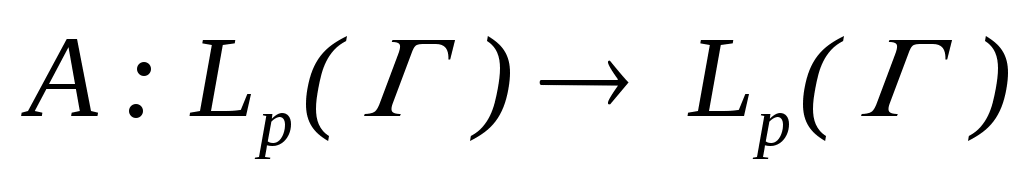 ограниченный и положительный. ограниченный и положительный.
Тогда при каждом  уравнение (I) имеет решение в уравнение (I) имеет решение в 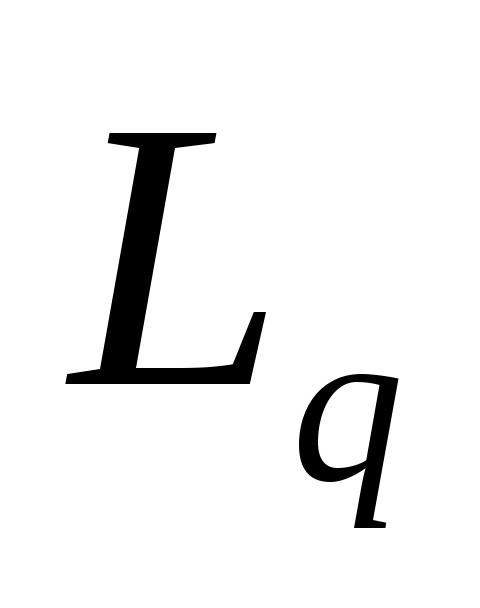 . Если, кроме того, хотя бы один из операторов А или F строго монотонен, то это решение единственное в . Если, кроме того, хотя бы один из операторов А или F строго монотонен, то это решение единственное в 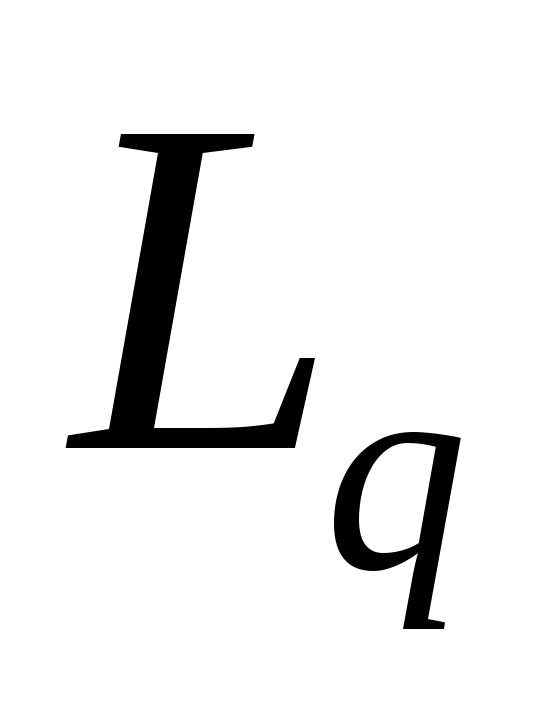 . .
Доказательство. Если в уравнении (I) сделать замену 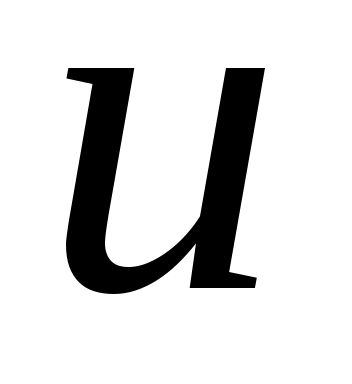 на на  а вместо а вместо  написать написать  , то у нас получится уравнение в котором , то у нас получится уравнение в котором 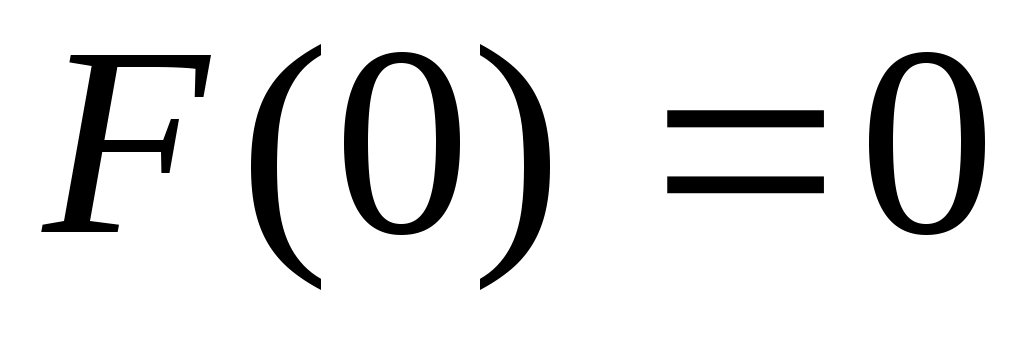 , а вместо , а вместо  будет будет 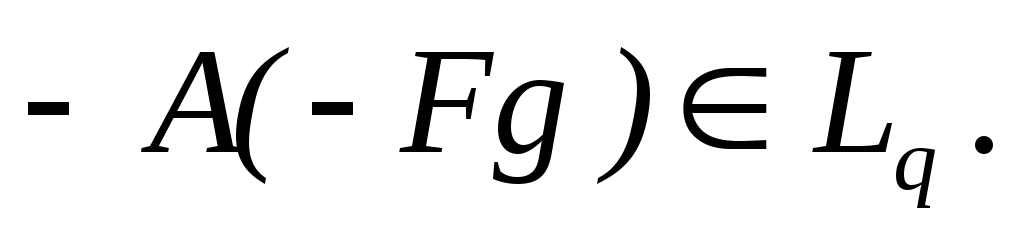 В дальнейшем В дальнейшем  и и  будем считать такими. будем считать такими.
Рассмотрим вспомогательное уравнение

где  - оператор сопряжённый A, n - натуральное число. Оператор - оператор сопряжённый A, n - натуральное число. Оператор 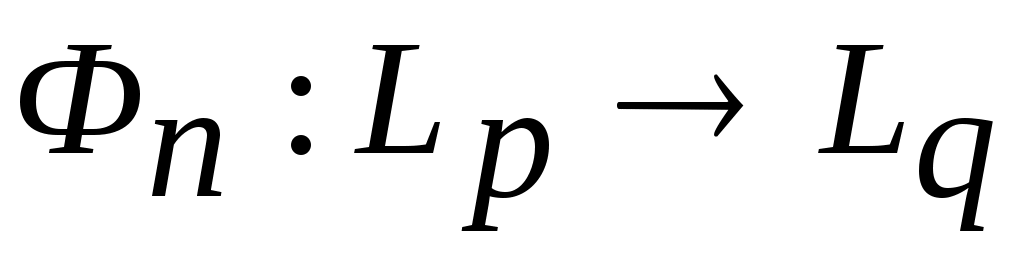 , очевидно, непрерывный и монотонный. Из коэрцитивности первого слагаемого и положительности остальных двух операторов следует коэрцитивность оператора , очевидно, непрерывный и монотонный. Из коэрцитивности первого слагаемого и положительности остальных двух операторов следует коэрцитивность оператора  при каждом фиксированном n. Поэтому уравнение при каждом фиксированном n. Поэтому уравнение 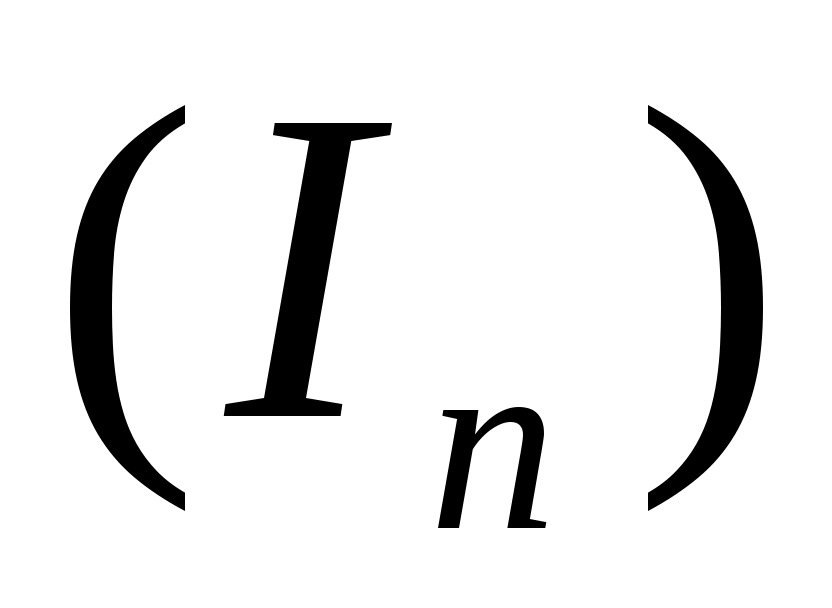 имеет решение имеет решение  (см.[4]). Из положительности каждого слагаемого в Фn следует, что (см.[4]). Из положительности каждого слагаемого в Фn следует, что

т.е. что последовательность  равномерно ограничена числом равномерно ограничена числом  . Интегрируя обе части . Интегрируя обе части  в в 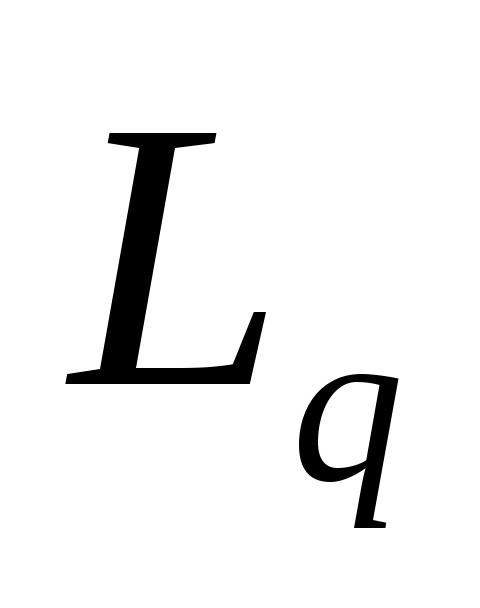 , получим , получим
 . .
Из условия (1) имеем
 . .
Из последнего с учётом  и и  , получим ограниченность последовательности , получим ограниченность последовательности Умножая обе части Умножая обе части 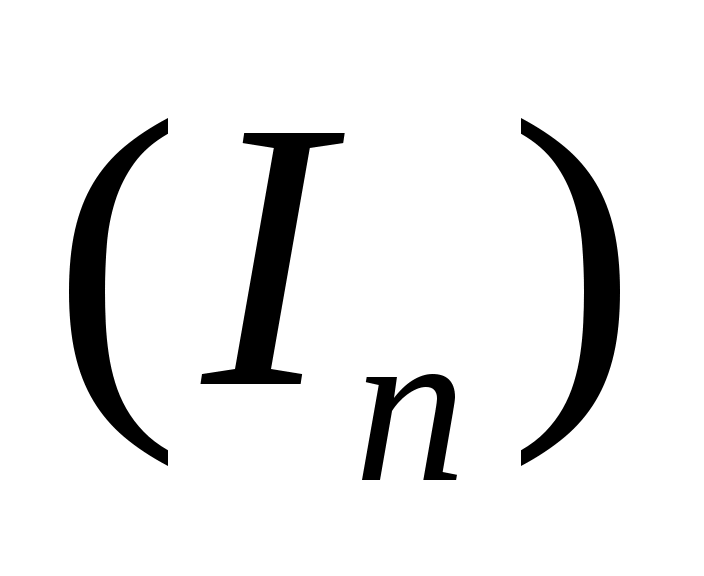 на на  , получим , получим

Отсюда следует равномерная ограниченность последовательности  Из последнего следует, что Из последнего следует, что

Из ограниченности  следует существование слабо сходящейся к следует существование слабо сходящейся к 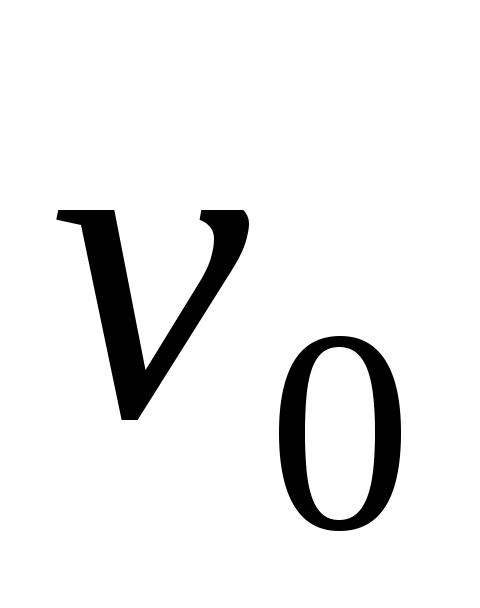 подпоследовательности подпоследовательности 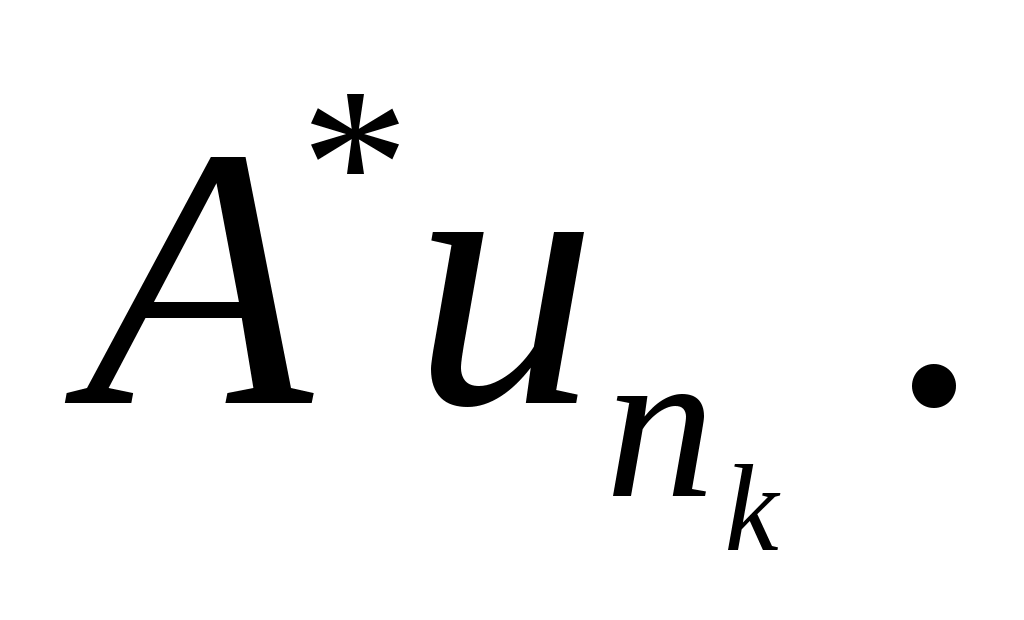
Монотонность оператора
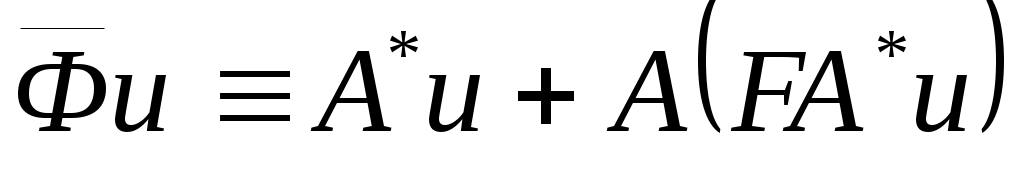
и сильная сходимость в  к нулю первого слагаемого в к нулю первого слагаемого в 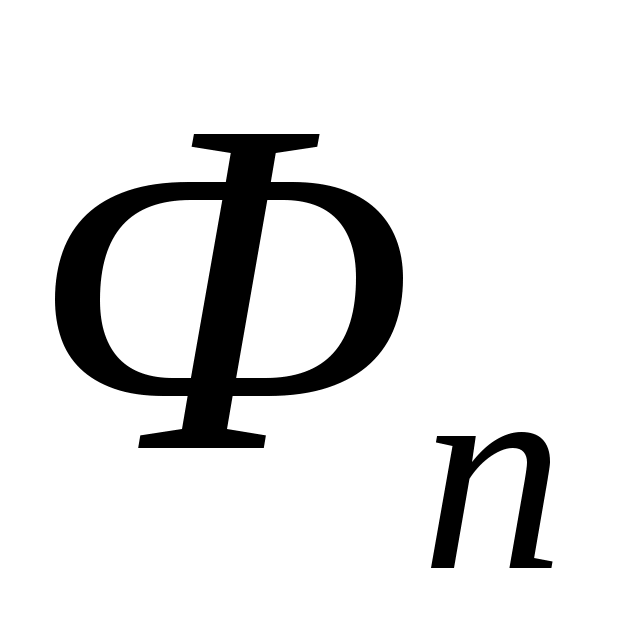 дает слабую дает слабую
сходимость  к к  . .
Из монотонности  следует, что существует следует, что существует  для которой верно для которой верно

почти всюду, т. е.  является решением уравнения (I). является решением уравнения (I).
Единственность решения вытекает непосредственно из уравнения (I).
Пусть  и и 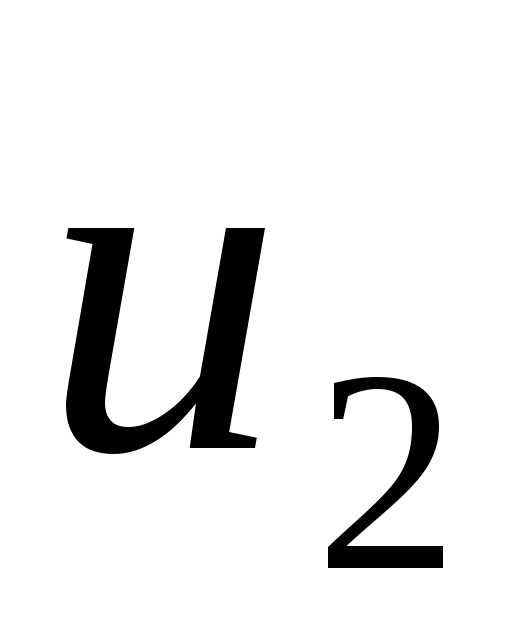 – разные решения уравнения. Тогда получим – разные решения уравнения. Тогда получим

Умножая обе части последнего равенства на выражение в скобках и интегрируя с мерой  , получим , получим

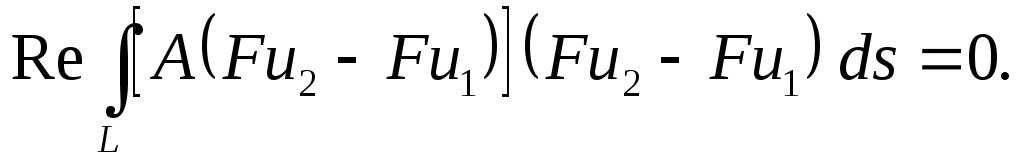 Если Если  строго монотонный, то из первого равенства следует строго монотонный, то из первого равенства следует 
Если оператор  строго монотонный, то строго монотонный, то   и уже из уравнения (I) следует и уже из уравнения (I) следует 
Следствие 1.1. Если оператор  в теореме ограничен в в теореме ограничен в  и и  - решение уравнения (I) из - решение уравнения (I) из  , то , то  Это следует из того, что Это следует из того, что 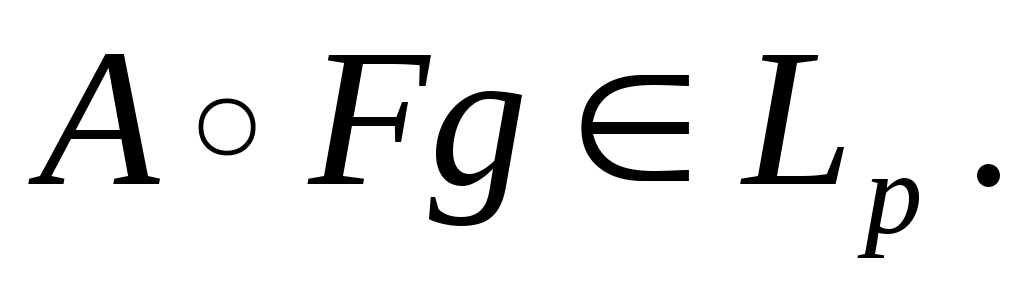
Следствие 1.2. Если в неравенстве (1) нет  , т.e. , т.e.  , то при любом измеримом , то при любом измеримом  уравнение имеет решение уравнение имеет решение  такое, что такое, что 
Это следует из того, что 
Замечание 1.1. В теореме ограничение  является в целом необходимым. Мы построили пример линейного оператора является в целом необходимым. Мы построили пример линейного оператора  и монотонного и монотонного

при которых уравнение (I) заведомо не имеет решения.
Пусть
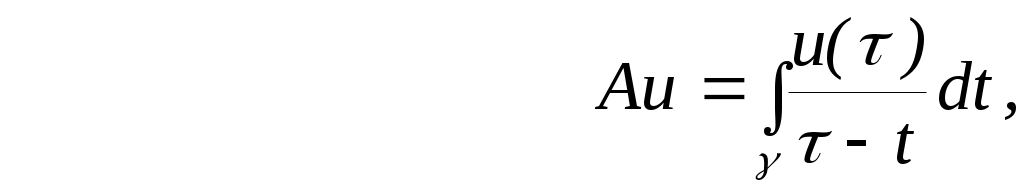
где  - единичная окружность с центром в точке (0,0). В следующем пункте 2 доказывается, что - единичная окружность с центром в точке (0,0). В следующем пункте 2 доказывается, что  – положительный оператор. – положительный оператор.
На единичной окружности функцию из   всегда можно разложить в ряд всегда можно разложить в ряд

Но если подставить  в оператор в оператор  , мы получим , мы получим
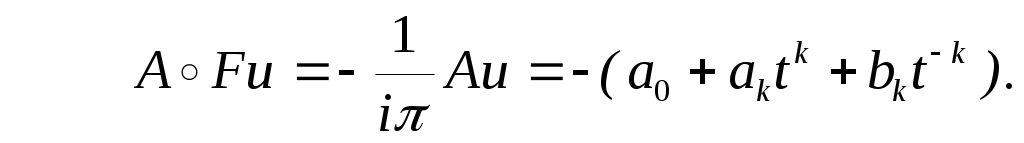
Значит

для любых 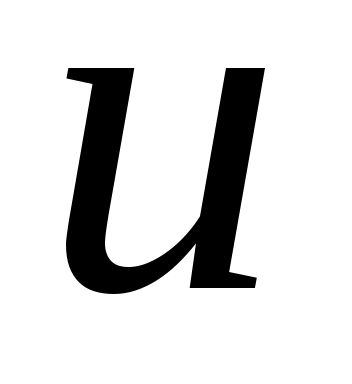 из из . Если в правой части взять . Если в правой части взять  при любом натуральном при любом натуральном  , то уравнение (I) не имеет решения ни в каком известном пространстве. , то уравнение (I) не имеет решения ни в каком известном пространстве.
Этот пример говорит и о необходимости существенных дополнительных ограничений на операторы  или или  при доказательстве гипотетического утверждения теоремы 3 работы [1]. при доказательстве гипотетического утверждения теоремы 3 работы [1].
Эти авторы так и поступили при доказательстве соответствующих утверждений в работах [3], [4].
Рассмотрим теперь уравнение (II).
Теорема 1.2. Пусть оператор  удовлетворяет условиям предыдущей теоремы, оператор удовлетворяет условиям предыдущей теоремы, оператор  - линейный ограниченный в любом - линейный ограниченный в любом  , положительный, кроме того , положительный, кроме того

Тогда уравнение (II) имеет решение в 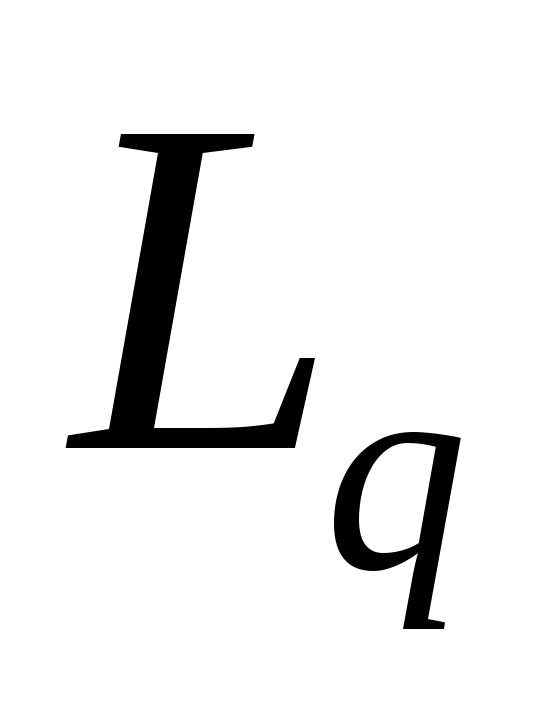 . .
Если, кроме того, хотя бы один из операторов  или или 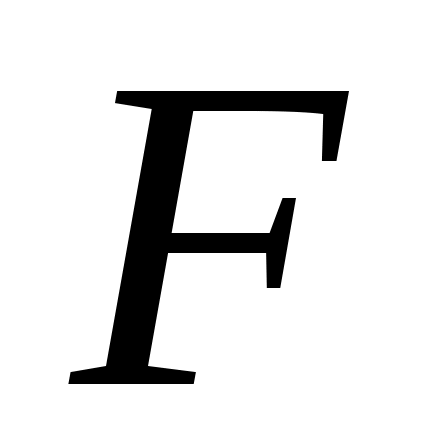 строго монотонен, то это решение единственное в строго монотонен, то это решение единственное в 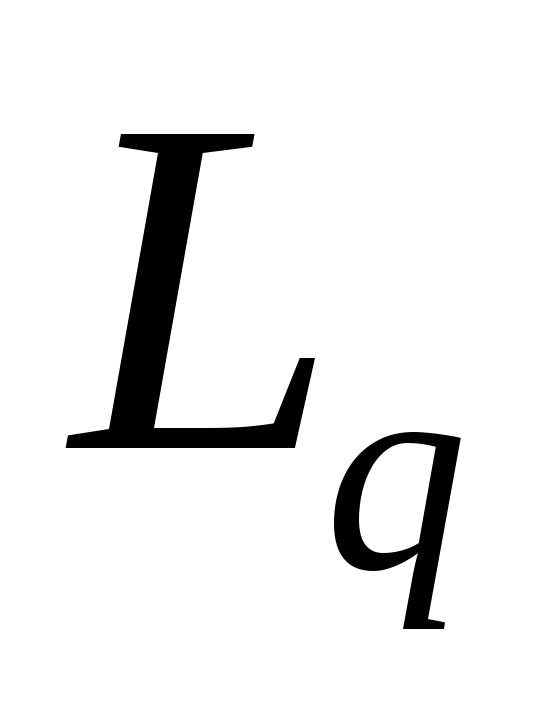 . .
Для доказательства строятся уравнения

Первое и третье слагаемые действуют из 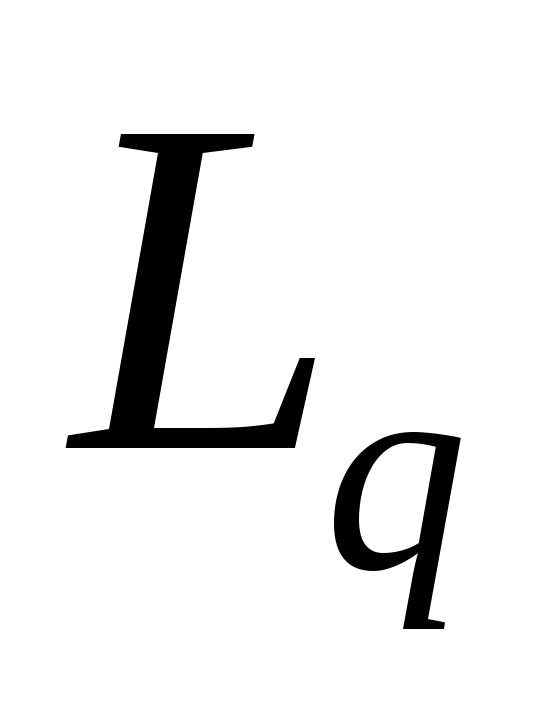 в в  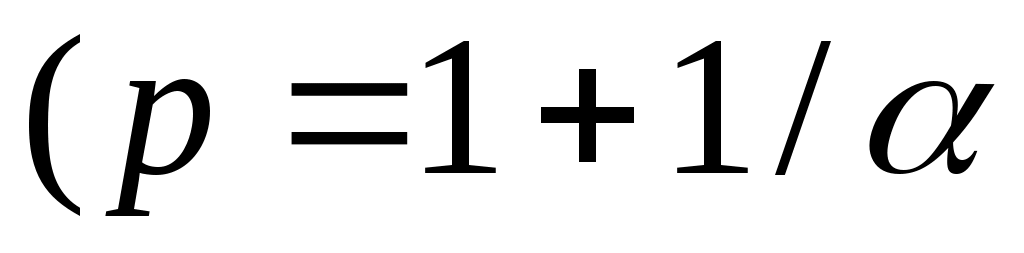 , ,  , являются непрерывными множествами, и их сумма является коэрцитивной в , являются непрерывными множествами, и их сумма является коэрцитивной в 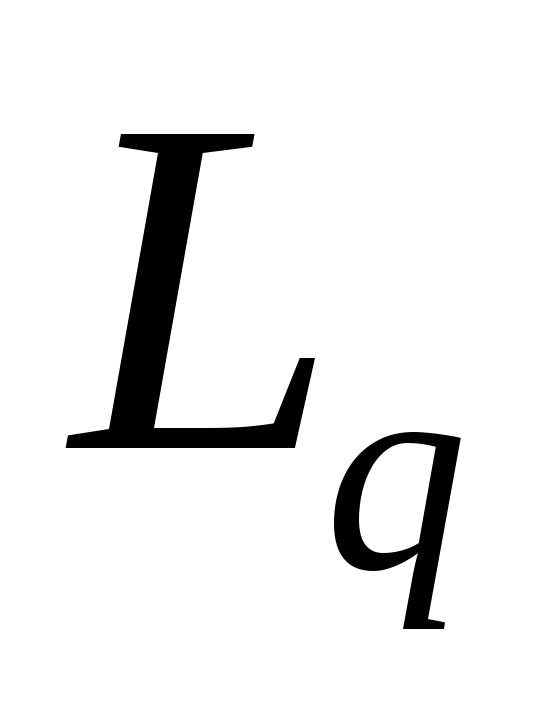 . Оператор . Оператор  положительный в том смысле, что положительный в том смысле, что  при любом при любом 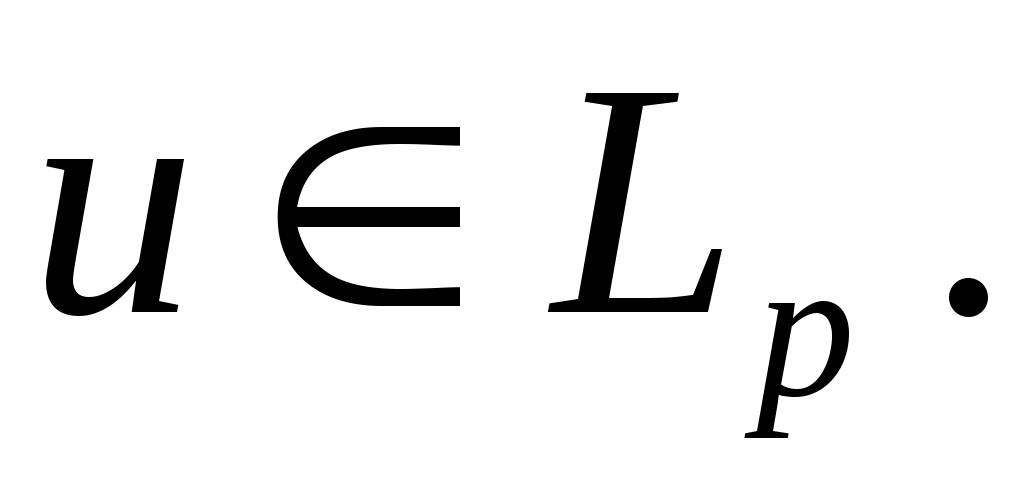
Берем общий для  и и 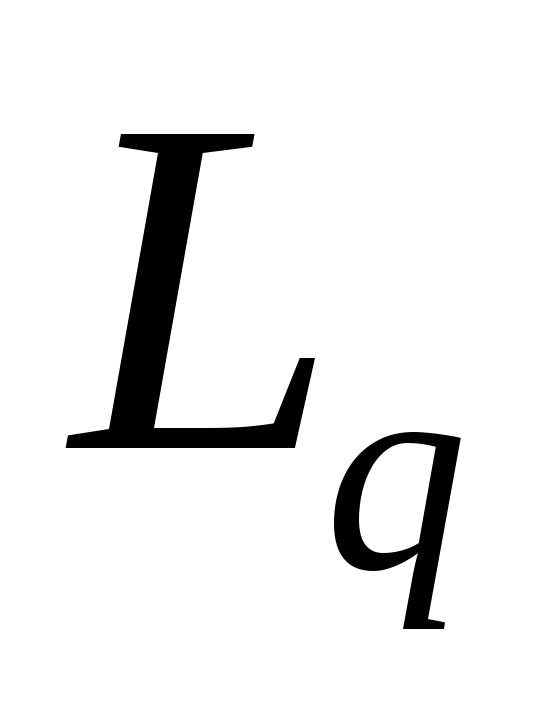 базис базис 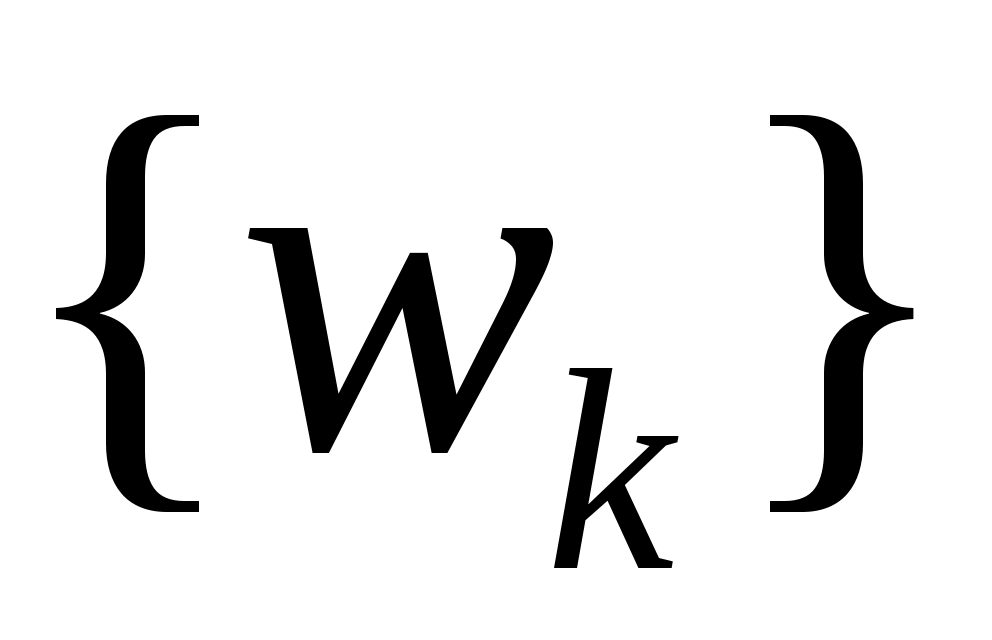 и составим подпространства из многочленов и составим подпространства из многочленов  , ,  . В этих подпространствах нормы эквивалентны и оператор . В этих подпространствах нормы эквивалентны и оператор 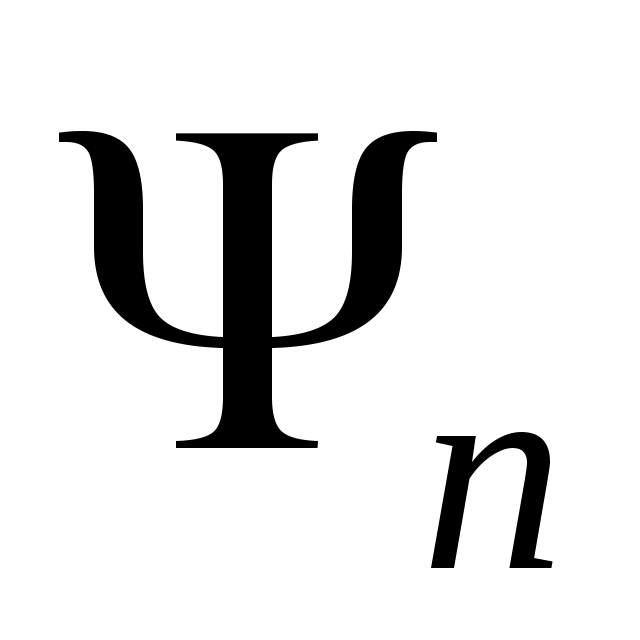 коэрцитивный как оператор из коэрцитивный как оператор из 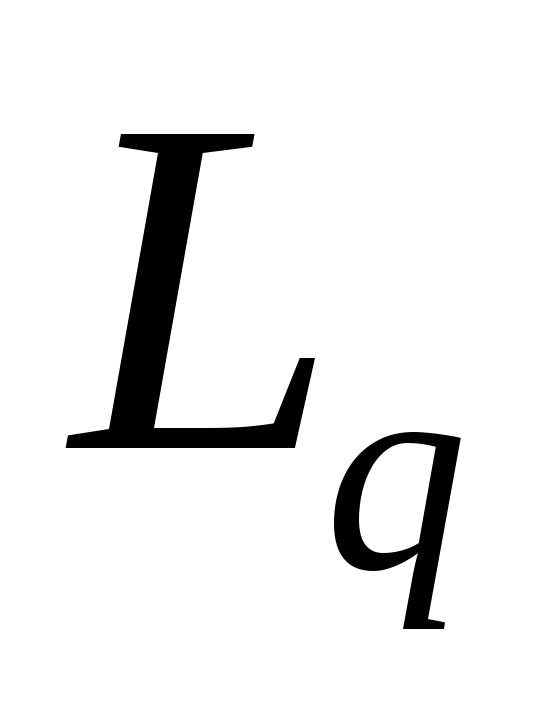 в в  . Значит уравнение . Значит уравнение  имеет решение имеет решение  в каждом в каждом  , имеющий такой смысл, что , имеющий такой смысл, что
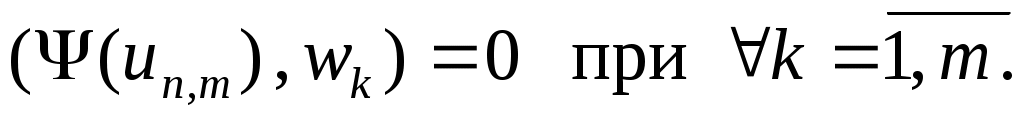
Из коэрцитивности  следует равномерная ограниченность множества следует равномерная ограниченность множества  в в 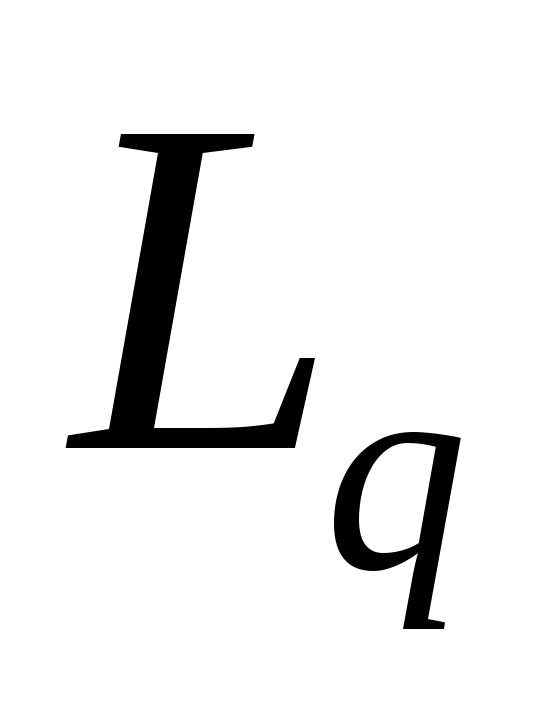 . Используя монотонность . Используя монотонность 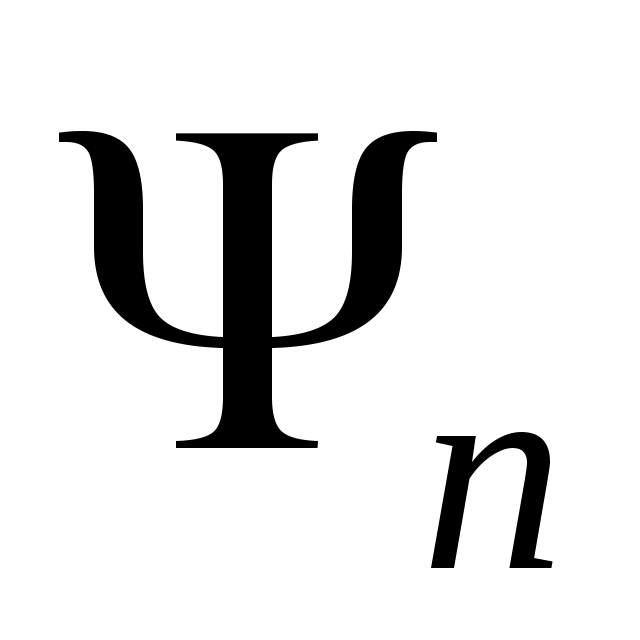 мы получим существование слабого предела мы получим существование слабого предела  подпоследовательности из подпоследовательности из  , которая является решением , которая является решением  . Но поскольку первое и третье слагаемые в . Но поскольку первое и третье слагаемые в  принадлежат принадлежат  , то и , то и 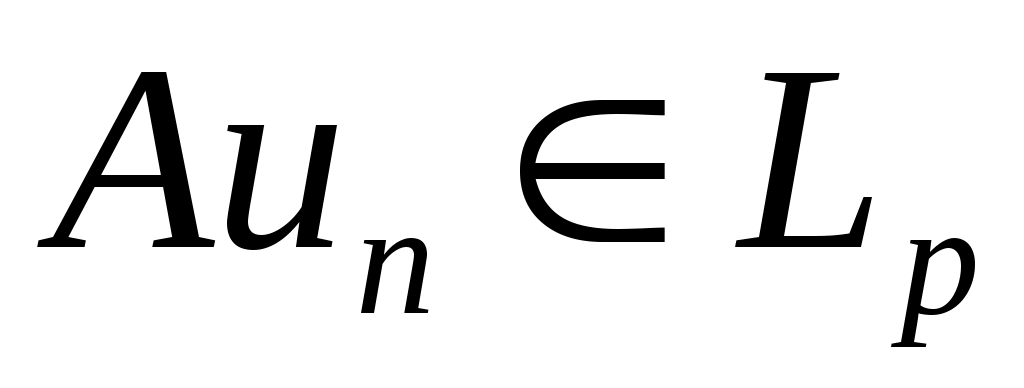 . .
Из тождества  и положительности и положительности  следует ограниченность множества следует ограниченность множества 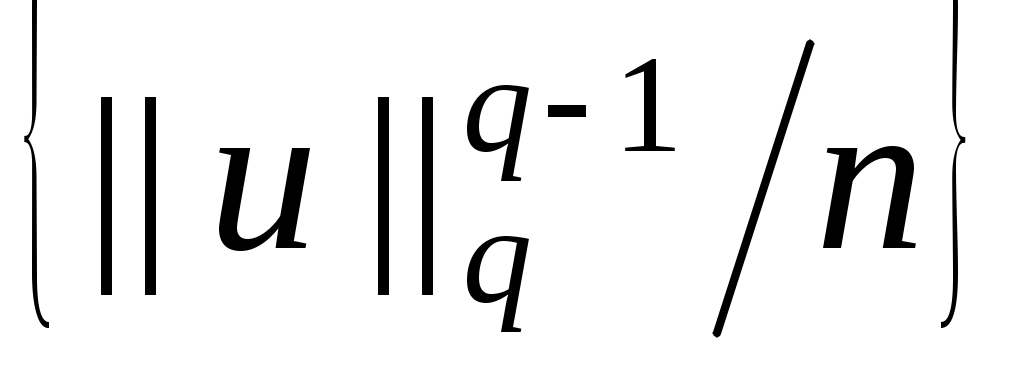 числом числом 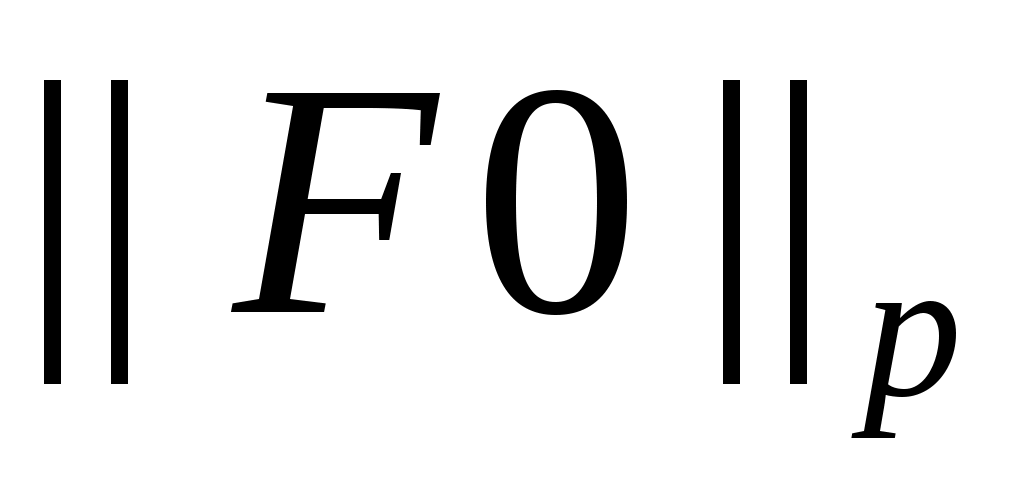 . .
Используя условия (1) и (2) получается

С учетом  , ограниченности первого слагаемого в неравенстве, , ограниченности первого слагаемого в неравенстве,  , мы получаем равномерную ограниченность , мы получаем равномерную ограниченность 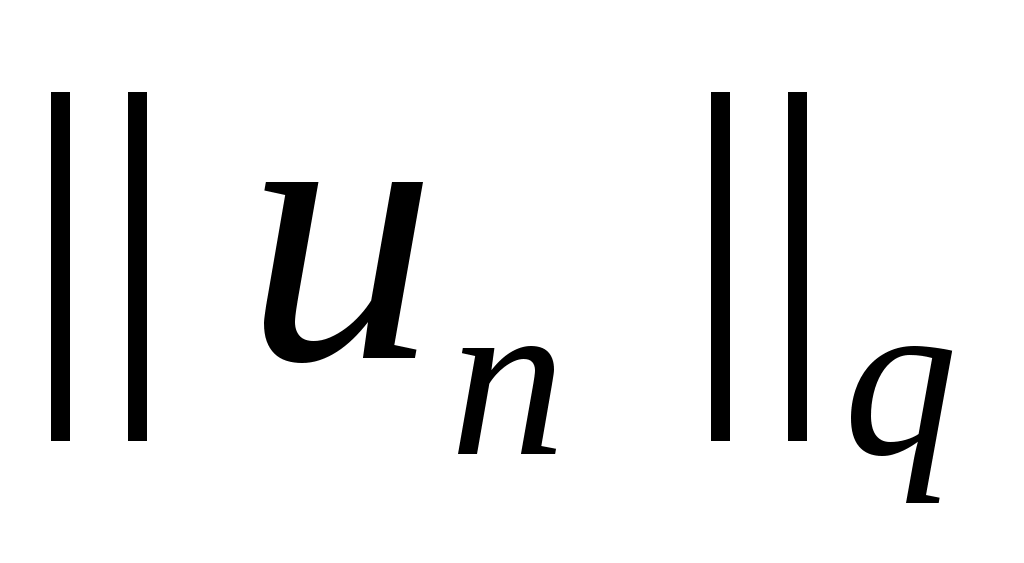 . Значит из . Значит из 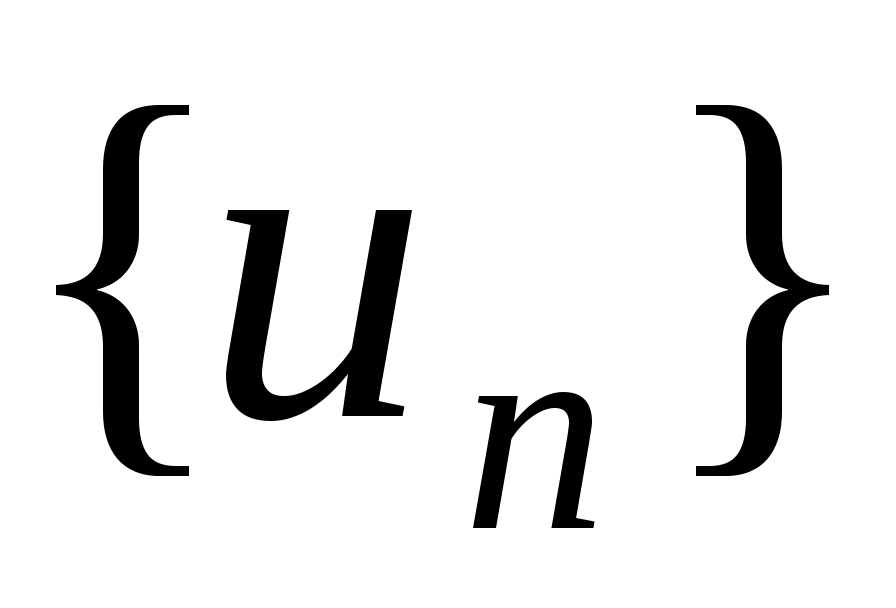 можно выделить подпоследовательность можно выделить подпоследовательность  такую, что такую, что  , ,  , ,  сходятся слабо к сходятся слабо к  , ,  , ,  соответственно. Первое слагаемое в соответственно. Первое слагаемое в  сходится к нулю по норме в сходится к нулю по норме в  . Пользуясь монотонностью . Пользуясь монотонностью  , мы получим , мы получим  , причем, , причем, 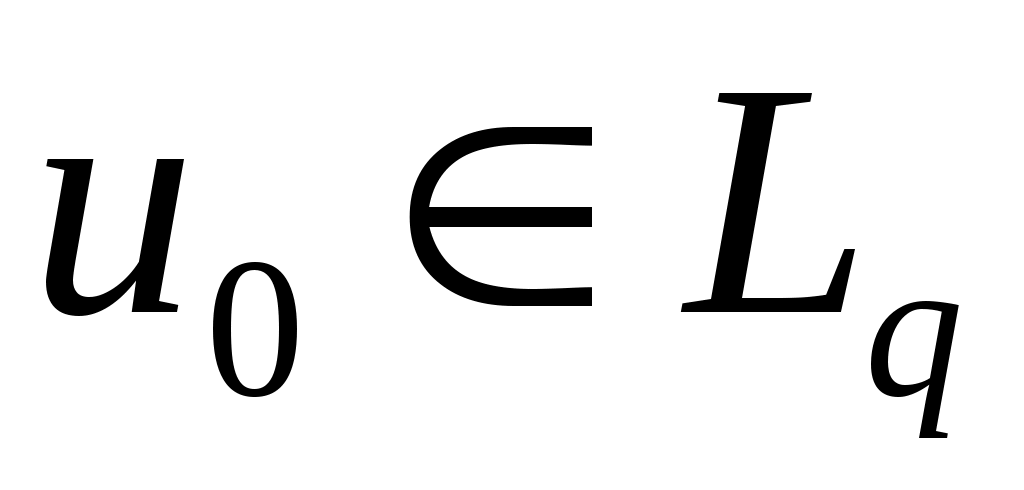 , ,  . Значит, . Значит, 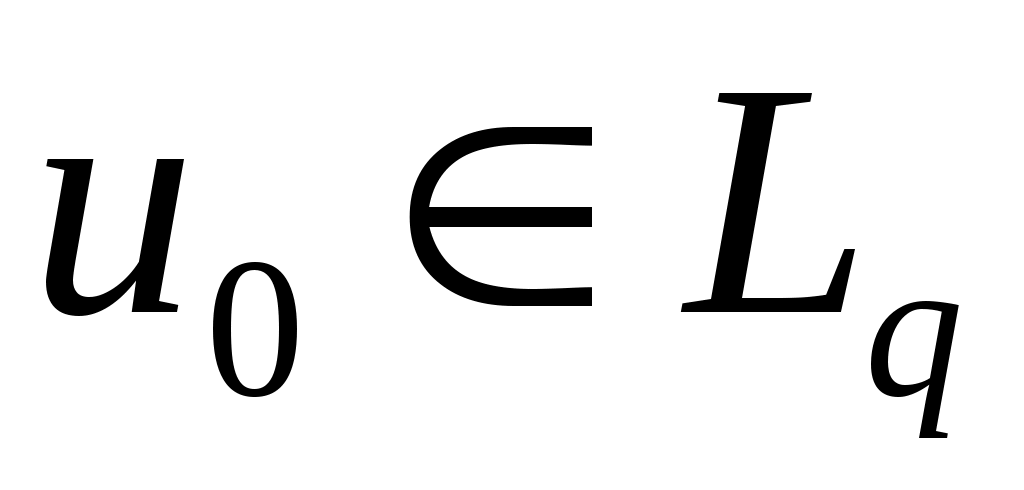 является решением уравнения (II). является решением уравнения (II).
Единственность решения доказывается как в предыдущей теореме.
Замечание 1.2. Если  , то решение уравнения существует в , то решение уравнения существует в  при тех же условиях теоремы 2. при тех же условиях теоремы 2.
Теорема 1.3. Пусть функция 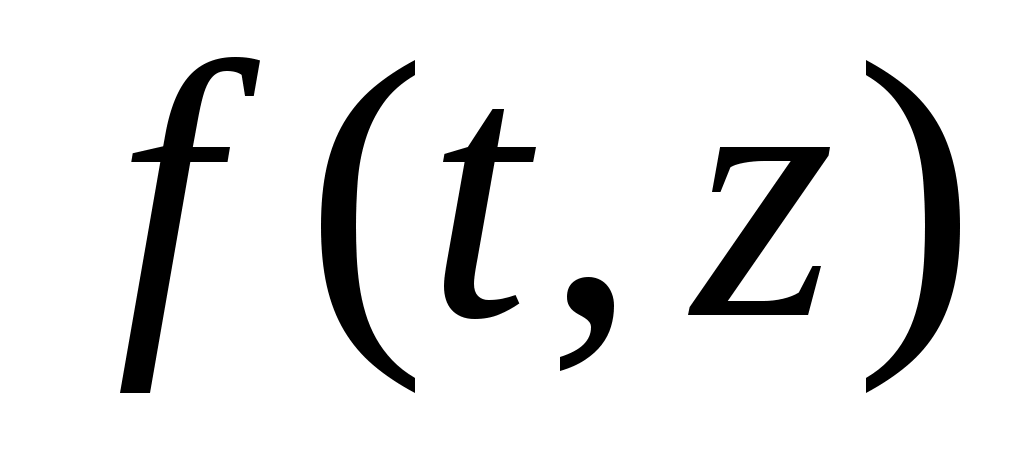 удовлетворяет неравенствам удовлетворяет неравенствам

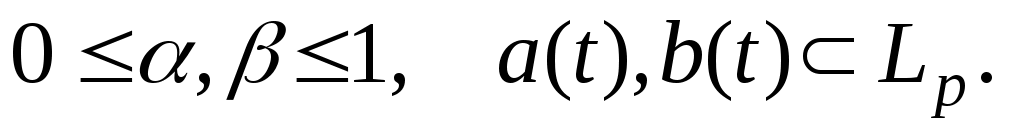
Пусть далее  – линейный непрерывный и положительный оператор при – линейный непрерывный и положительный оператор при  . Тогда уравнение (II) имеет решение в . Тогда уравнение (II) имеет решение в   . .
Доказательство. В случае  оператор оператор  непрерывный, монотонный в непрерывный, монотонный в  , а из левой части (3) следует его коэрцитивность в , а из левой части (3) следует его коэрцитивность в  . Значит, уравнение имеет решение в . Значит, уравнение имеет решение в  . .
При  строим такую “срезку” строим такую “срезку”  функции функции  , чтобы , чтобы

с сохранением монотонности 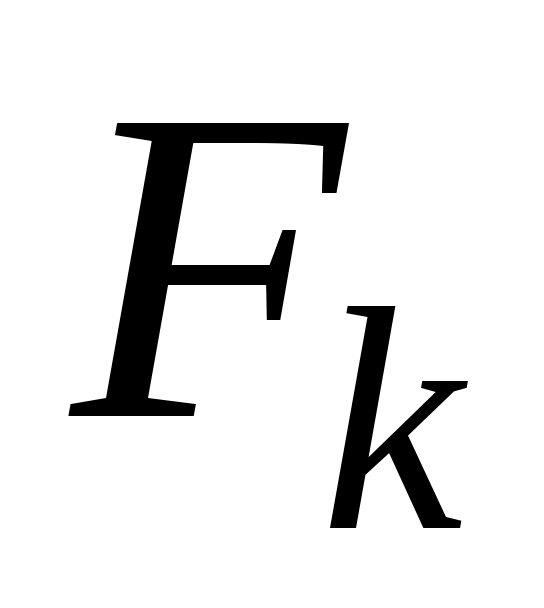 по по  . Возможность такого построения . Возможность такого построения 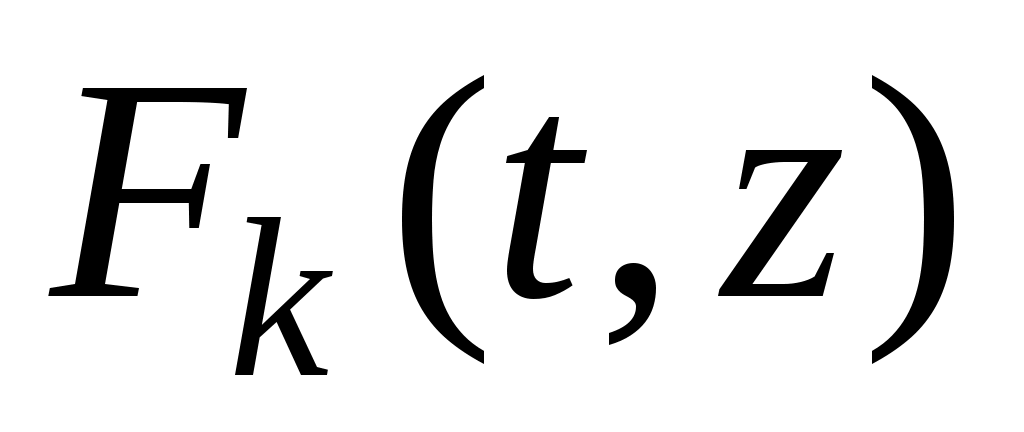 геометрически очевидна. В достаточно большом круге геометрически очевидна. В достаточно большом круге  функции функции 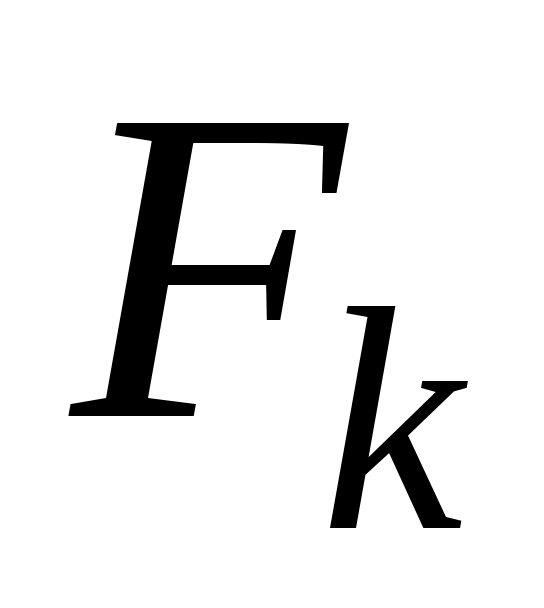 и и 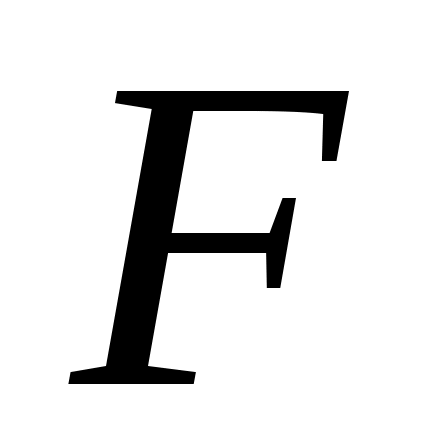 совпадают, а дальше строятся совпадают, а дальше строятся 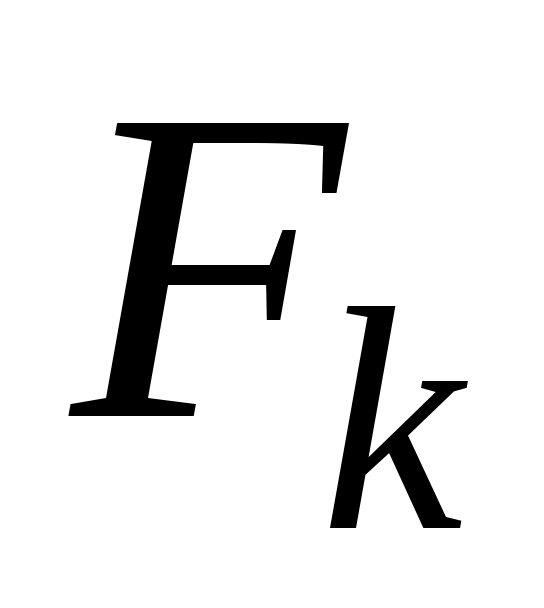 так, чтобы сохранить непрерывность и монотонность по z, конечно так, чтобы сохранить непрерывность и монотонность по z, конечно  . .
При каждом фиксированном  доказательство существования мы уже отметили, ибо доказательство существования мы уже отметили, ибо  . Значит, мы имеем последовательность . Значит, мы имеем последовательность  такую, что такую, что
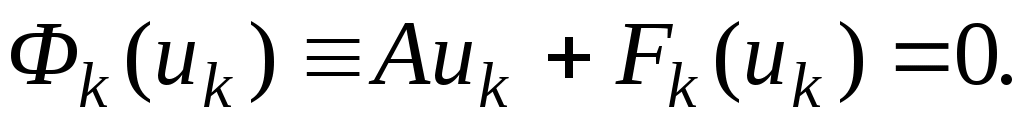
Из положительности  и из (3) следует, что и из (3) следует, что

и что последовательность  равномерно ограничена в равномерно ограничена в  . .
Из (3) также следует, что последовательность  ограничена в ограничена в  , , 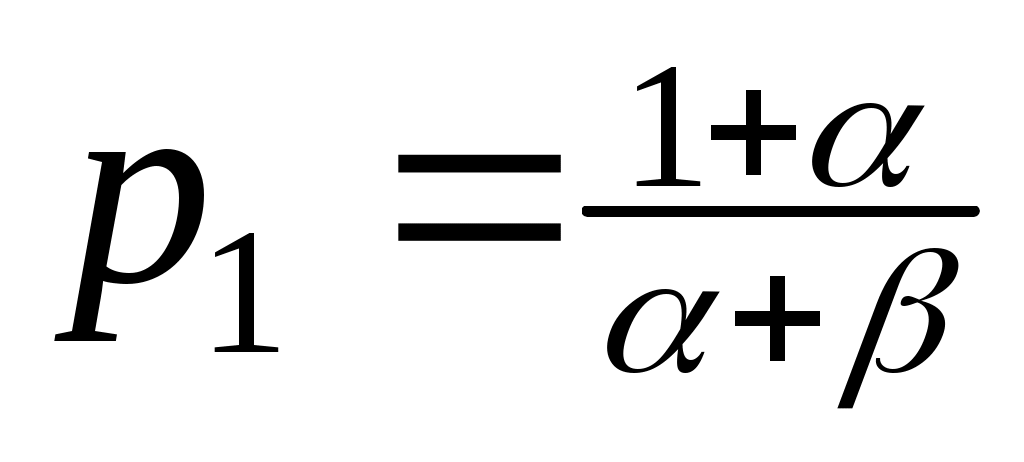 . Значит, существует подпоследовательность . Значит, существует подпоследовательность  , ,  , , 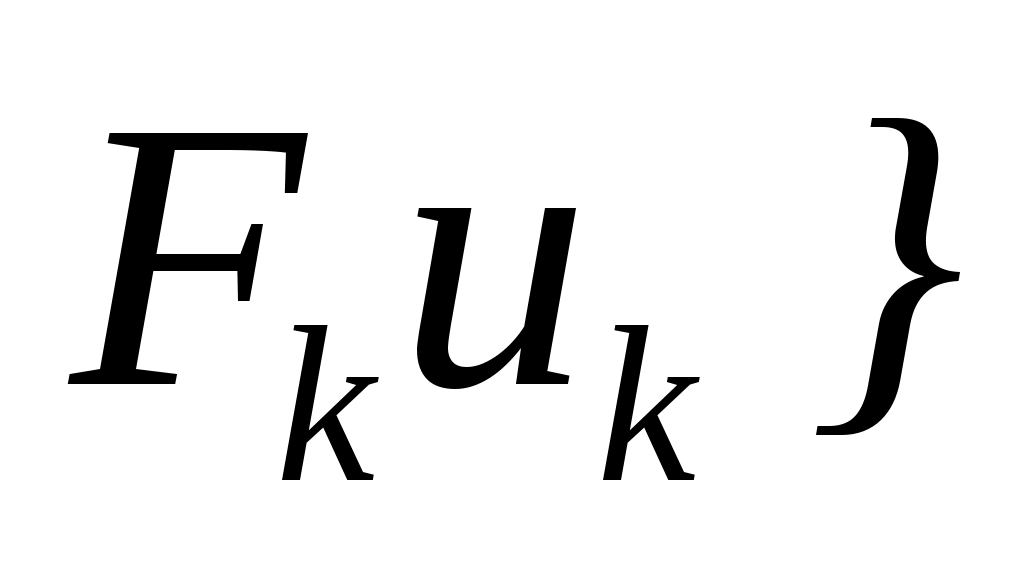 , которая слабо сходятся в пространстве , которая слабо сходятся в пространстве  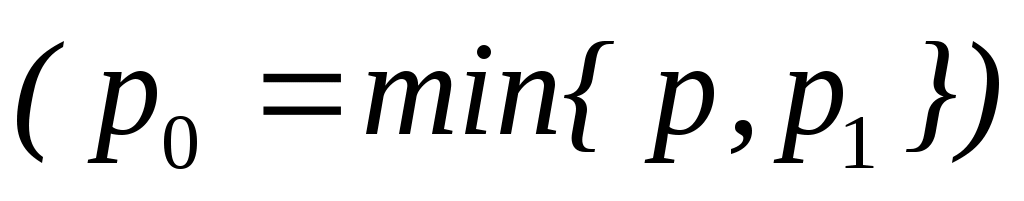 к к  , ,  , ,  и и

Из построения 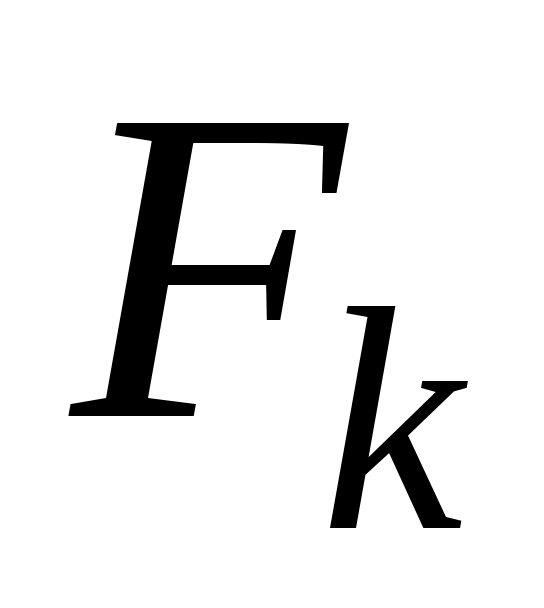 следует, что следует, что 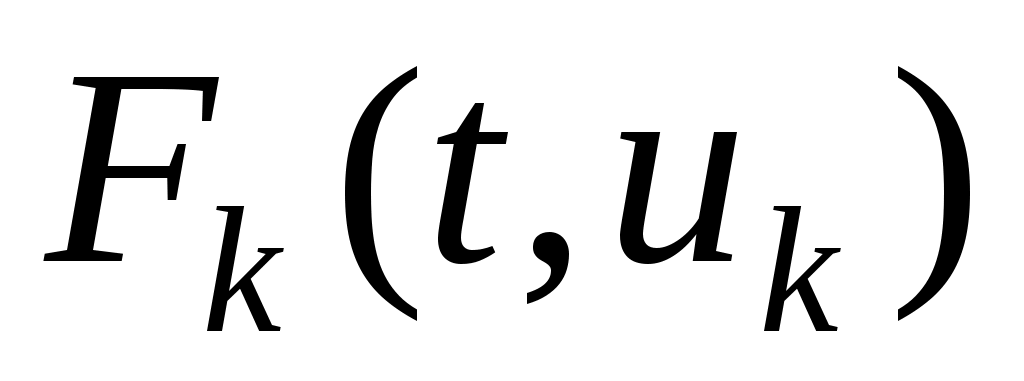 стремится к стремится к  по норме в по норме в 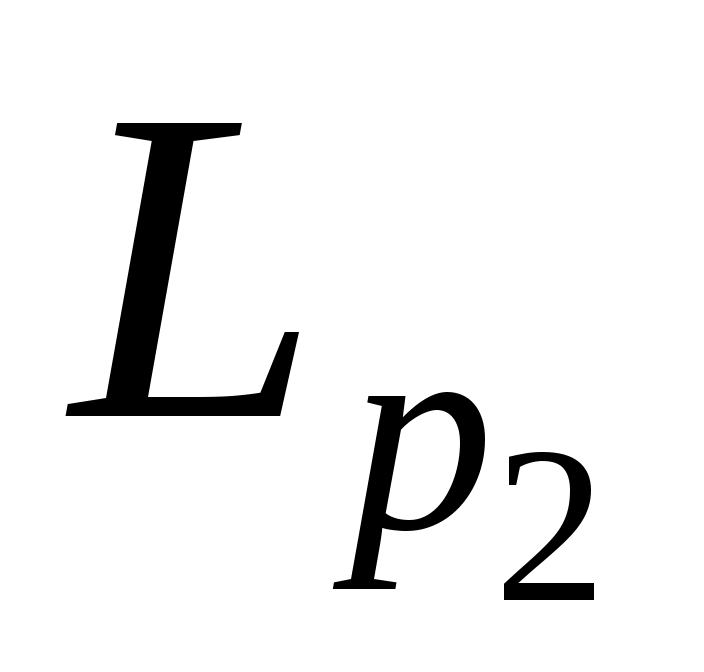 . Значит, . Значит,  есть слабый предел есть слабый предел  . .
Используя монотонность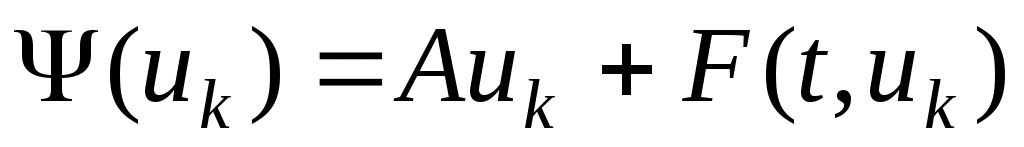 , получим, что , получим, что  , т. е. что , т. е. что  есть решение уравнения из есть решение уравнения из  . .
Замечание 1.3. Единственность решения, как и в предыдущей теореме, следует, если  или или  строго монотонны по строго монотонны по  . .
Следствие 1. 3. Если для 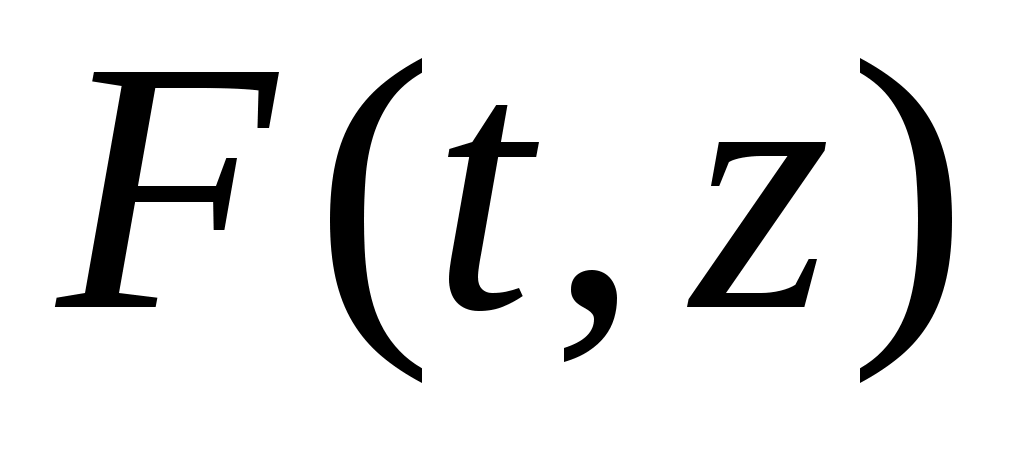 существует обратная функция существует обратная функция
 , ,
которая удовлетворяет условиям теоремы 1.3, то уравнение (I) сводится к (II) и уравнение (I) имеет решение в соответствующем   . .
2. Применение к нелинейным уравнениям с сингулярными интегралами
Обозначим через   линейные сингулярные интеграль-ные операторы линейные сингулярные интеграль-ные операторы
 , ,
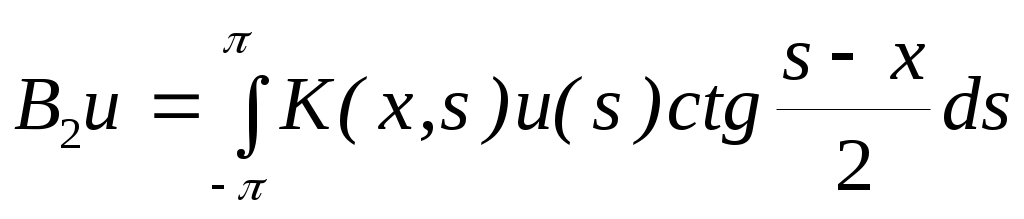 , ,
где γ - единичная окружность на комплексной плоскости, функция 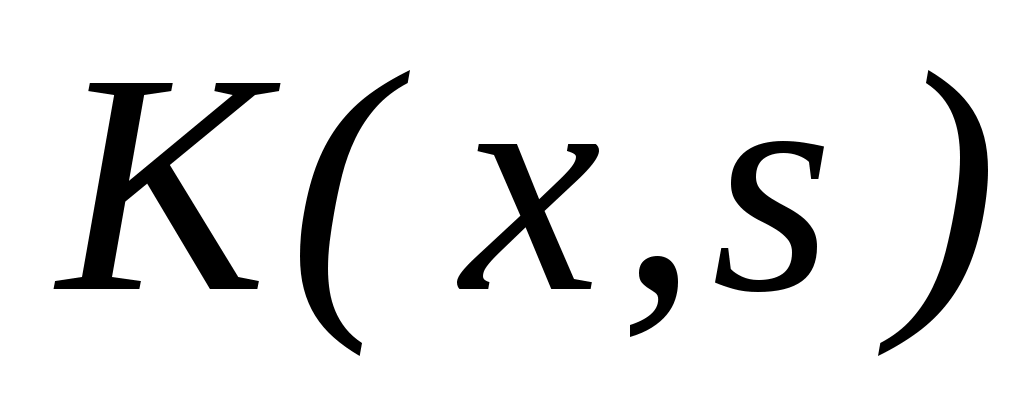 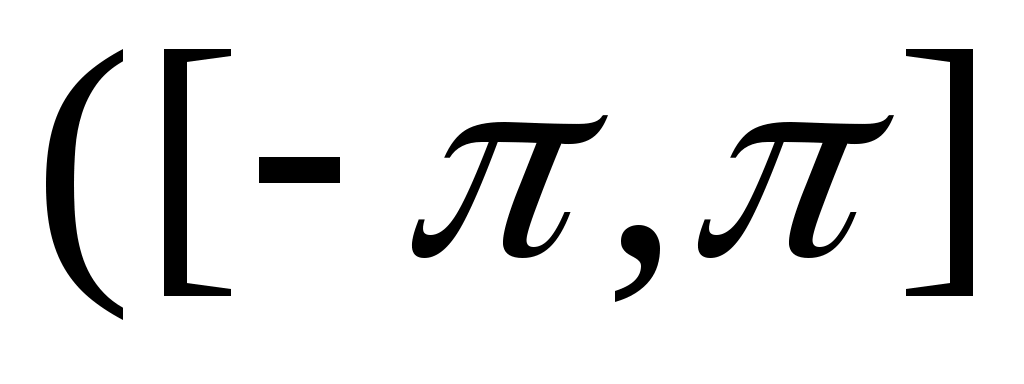 , , принадлежит принадлежит 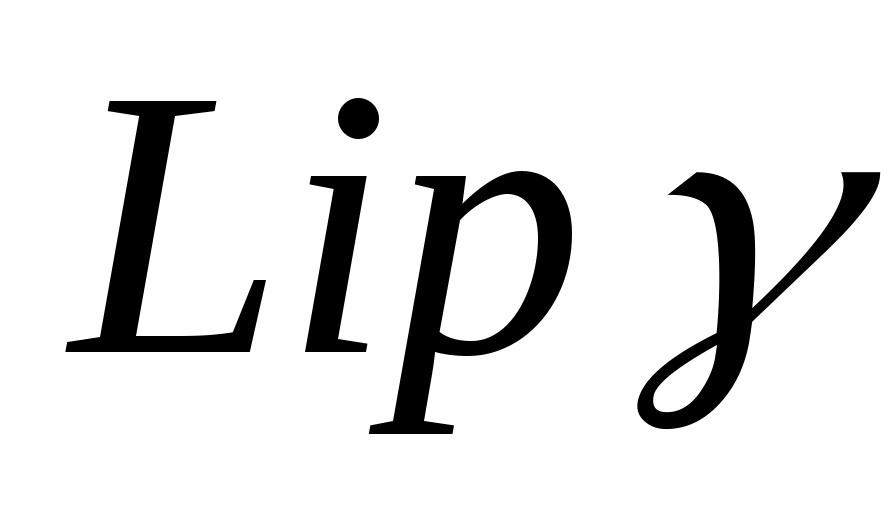 и симметрична относительно своих аргументов. и симметрична относительно своих аргументов.
Лемма 2.1. Операторы   ограничены и положительны при ограничены и положительны при  и и
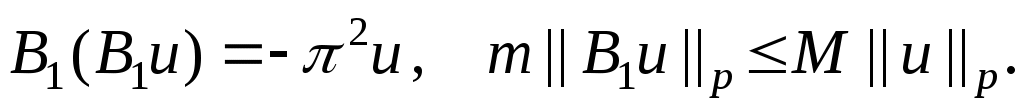
Положительность оператора  получается непосредственно из разложения получается непосредственно из разложения



Для оператора 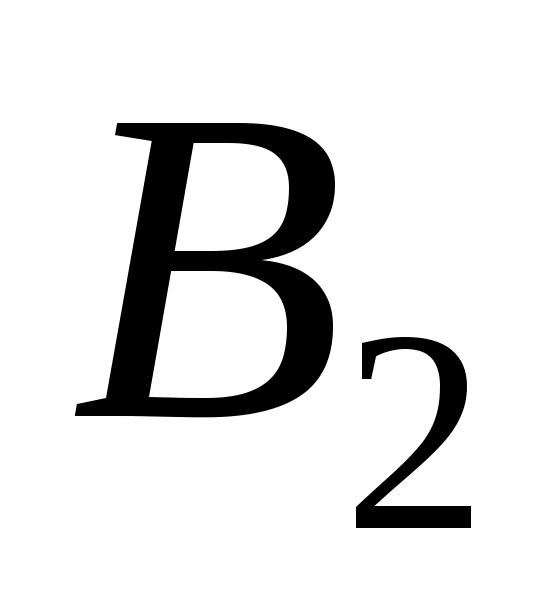 непосредственно имеем непосредственно имеем

откуда следует, что
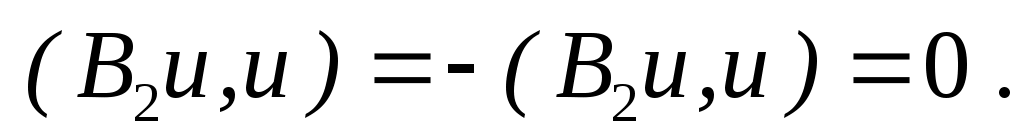
Ограниченность операторов  известна из классической теоремы Рисса (см., напр., [7]). Ограниченность известна из классической теоремы Рисса (см., напр., [7]). Ограниченность  снизу прямо следует из снизу прямо следует из
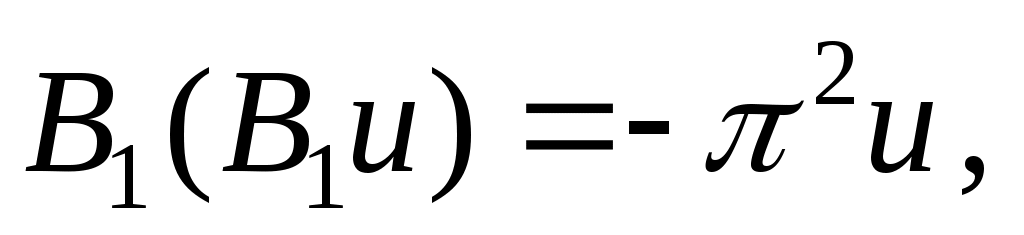
которое получается непосредственно, разлагая  в ряд Лорана на единичной окружности . в ряд Лорана на единичной окружности .
Замечание 2.1. Некоторая формула обратимости имеет место и для оператора  при при  , а именно , а именно

Это обращение следует из

Оператор  удовлетворяет всем условиям, накладываемым на оператор удовлетворяет всем условиям, накладываемым на оператор  в теоремах предыдущего параграфа. Поэтому теоремы 1.1 – 1.3 останутся справедливыми, если в них оператор в теоремах предыдущего параграфа. Поэтому теоремы 1.1 – 1.3 останутся справедливыми, если в них оператор  заменить на заменить на  . Только оператор . Только оператор  не является строго монотонным, поэтому для получения единственности строгая монотонность накладывается на функцию не является строго монотонным, поэтому для получения единственности строгая монотонность накладывается на функцию 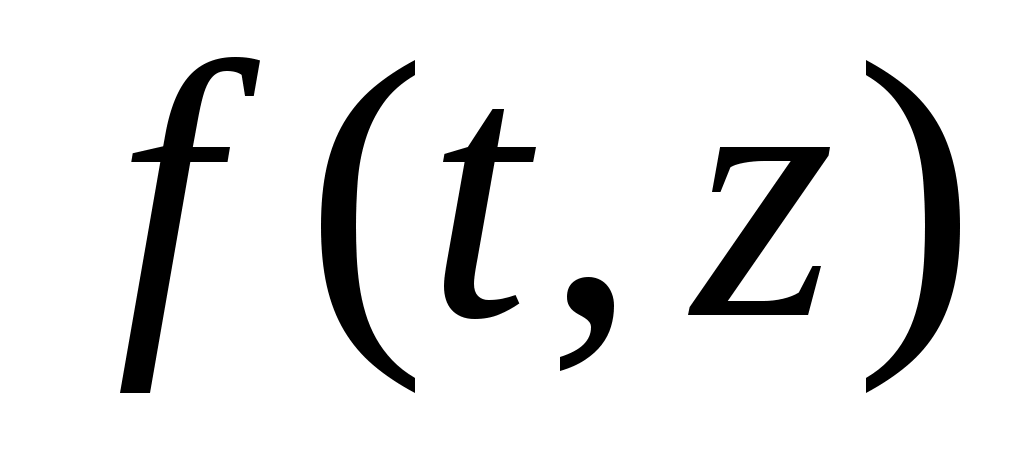 . .
Поскольку оператор  самообратим, то теоремы 1.1 - 1.3 применимы и для уравнения (I). самообратим, то теоремы 1.1 - 1.3 применимы и для уравнения (I).
Оператор  в общем случае не ограничен в в общем случае не ограничен в  снизу, поэтому в теореме 1.2 нельзя заменить снизу, поэтому в теореме 1.2 нельзя заменить  на на  . Но если взять . Но если взять  , то такой , то такой  ограничен снизу в некотором подпространстве ограничен снизу в некотором подпространстве  Функция Функция  из из  принадлежит принадлежит  , если имеет место , если имеет место
 , ,
т.е. при разложении  в тригонометрический ряд в тригонометрический ряд  . .
Поскольку правая часть g уравнения (I) можно полагать  , то уравнение (I) при , то уравнение (I) при  можно исследовать в таких подпространствах. Сопряжённым для можно исследовать в таких подпространствах. Сопряжённым для  в в  тоже является ( тоже является ( ), поэтому в теореме 1.2 можно считать ), поэтому в теореме 1.2 можно считать  . .
Применять теоремы 1.1-1.3 можно и к линейным сингулярным операторам. Но такие операторы обычно изучаются в пространствах действительных функций и для них получены более «хорошие» результаты.
ЛИТЕРАТУРА
Brézis H., Browder F.E. Some new result about Hammerstein equations. //Bull. Amer. Math. Sosiety. 1974. V. 80. P. 567-572.
Brézis H., Browder F.E. Nonlinear integral equations and systems of Hammerstein type. //Advances in Mathematics. 1975. V.18. P. 115-147.
Brézis H., Browder F.E. Maximal monotone operators in nonreflexive Banach spaces and nonlinear integral equations of Hammerstein type. //Bull. Amer. Math. Sosiety. 1975, V. 81. P. 82-88.
Вайнберг М. М. Вариационный метод и метод монотонных операторов. -М.: Наука. 1972, –416 с.
Магомедов Г.М., Ханикалов Х.Б. Теоремы разрешимости нелинейных уравнений второго рода и некоторые приложения. // Доклады AH СССР. 1983. Т.270. №5. С.1051-1053.
Магомедов Г.М., Ханикалов Х.Б. Исследование некоторых нелинейных уравнений второго рода с сингулярными интегралами. // Вестник ДГУ. 1999. Вып. 1. С.59-64.
Ханикалов Х.Б. Об одном подходе к исследованию уравнений типа Гаммерштейна. // Актуальные проблемы математики и смежные вопросы ( труды межвузовского семинара), Махачкала, ФГБОУ ВПО «ДГТУ», 2015.
С. 88-92.
Гахов Ф.Д. Краевые задачи. -М.: Наука. 1963. –624 с.
|
|
|
 Скачать 499 Kb.
Скачать 499 Kb.
