Нелинейные модели регрессии и их линеаризация
 Скачать 128.77 Kb. Скачать 128.77 Kb.
|
|
ТЕМА: Нелинейные модели регрессии и их линеаризация ЗАДАНИЕ: Изучить материал и прислать мне на Яндекс-диск протокол с решением в Excel данной задачи с указанием ФИО и даты в соответствующую предмету папку. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Пример 3.4. По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений ( Х, млн. руб. ).
Требуется: 1.Для характеристики Y от Х построить следующие модели: линейную (для сравнения с нелинейными), степенную, показательную, гиперболическую. 2.Оценить каждую модель, определив: индекс корреляции, среднюю относительную ошибку, коэффициент детерминации, F-критерий Фишера. 3.Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик. 4.Рассчитать прогнозные значения результативного признака по лучшей модели, если объем капиталовложений составит 89,573 млн. руб. 5.Результаты расчетов отобразить на графике. Решение:1. Построение линейной модели парной регрессии Определим линейный коэффициент парной корреляции по следующей формуле: 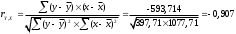 ; ;Можно сказать, что связь между объемом капиталовложений Х и объемом выпуска продукции Y обратная, достаточно сильная. Уравнение линейной регрессии имеет вид: ŷ = a + b x Таблица 3.5
Значения параметров a и b линейной модели определим, используя данные таблицы 3.5 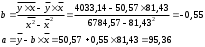 Уравнение линейной регрессии имеет вид: ŷ = 95,36 - 0,55 х С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс. руб. Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения этого недостатка. Рассчитаем коэффициент детерминации: R2 = r2yx = 0,822 Вариация результата Y (объема выпуска продукции) на 82,2 % объясняется вариацией фактора Х (объемом капиталовложений). Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера: 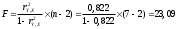 F>FТАБЛ = 6,61 для = 0,05 ; к1=m=1, k2=n-m-1=5. Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>FТАБЛ . Определим среднюю относительную ошибку: 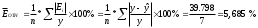 В среднем расчетные значения ŷ для линейной модели отличаются от фактических значений на 5,685 %. 2. Построение степенной модели парной регрессии Уравнение степенной модели имеет вид: 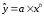 Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения: lg ŷ = lg a + b lg x
Обозначим Y = lg ŷ, X = lg x, A = lg a. Тогда уравнение примет вид: Y = A + b X - линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.6 Таблица 3.6
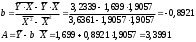 Уравнение регрессии будет иметь вид : Y=3.3991-0,8921 X Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.   Получим уравнение степенной модели регрессии: 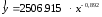 Определим индекс корреляции: 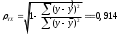 Связь между показателем y и фактором x можно считать достаточно сильной. Коэффициент детерминации: 0.836 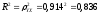 Вариация результата Y (объема выпуска продукции) на 83,6 % объясняется вариацией фактора Х (объемом капиталовложений). Рассчитаем F-критерий Фишера: 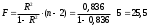 F>FТАБЛ = 6,61 для = 0,05. к1=m=1, k2=n-m-1=5 Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>FТАБЛ. Средняя относительная ошибка 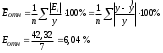 . .В среднем расчетные значения ŷ для степенной модели отличаются от фактических значений на 6,04 %. 3. Построение показательной функции Уравнение показательной кривой: ŷ = a b x Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения: lg ŷ = lg a + x lg b Обозначим Y = lg ŷ, B = lg b, A = lg a. Получим линейное уравнение регрессии: Y = A + B x . Рассчитаем его параметры, используя данные таблицы 3.7. Таблица 3.7.
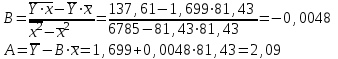 Уравнение будет иметь вид: Y=2,09-0,0048 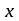 Перейдем к исходным переменным x и y, выполнив потенциирование данного уравнения: 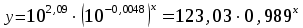 . .Определим индекс корреляции 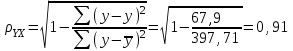 Связь между показателем y и фактором x можно считать достаточно сильной. Индекс детерминации: 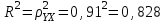 Вариация результата Y (объема выпуска продукции) на 82,8 % объясняется вариацией фактора Х (объемом капиталовложений). Рассчитаем F-критерий Фишера: 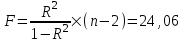 F>FТАБЛ = 6,61 для = 0,05 ; к1=m=1, k2=n-m-1=5 . Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>FТАБЛ . Средняя относительная ошибка: 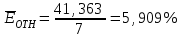 В среднем расчетные значения ŷ для показательной функции отличаются от фактических на 5.909 %. 4.Построение гиперболической функции Уравнение гиперболической функции : ŷ = a + b / x . Произведем линеаризацию модели путем замены Х = 1 / х. В результате получим линейное уравнение ŷ = a + b Х. Рассчитаем его параметры по данным таблицы 3.8 Таблица 3.8.
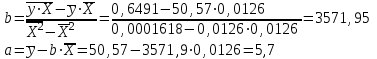 Получим следующее уравнение гиперболической модели: ŷ=5,7 + 3571,9 / х Определим индекс корреляции 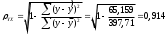 Связь между показателем y и фактором x можно считать достаточно сильной. Индекс детерминации: 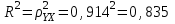 Вариация результата Y (объема выпуска продукции) на 83,5 % объясняется вариацией фактора Х (объемом капиталовложений). F-критерий Фишера: 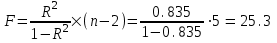 F>FТАБЛ = 6,61 для = 0,05 ; к1=m=1, k2=n-m-1=5 . Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>FТАБЛ . Средняя относительная ошибка 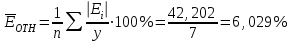 В среднем расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 6,029 %. Для выбора лучшей модели построим сводную таблицу результатов. Таблица 3.9.
Все модели имеют примерно одинаковые характеристики, но большее значение F – критерия Фишера и большее значение коэффициента детерминации R2 имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

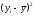
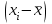
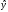
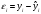
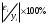
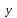
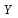
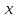
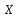
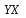
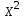
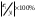
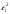
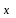
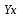
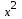
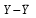
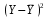
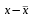
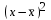
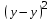
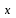
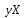
 араметры
араметры