|
|
Нелинейные уравнения с двумя переменными и их системы
Раздел:
|
Уравнения, неравенства с двумя переменными и их системы
|
ФИО педагога
|
Тойчиева С.Б.
|
Урок :2
|
|
Класс: 9
|
Количество присутствующих:
|
Количество
отсутствующих:
|
Тема урока
|
Нелинейные уравнения с двумя переменными и их системы
|
Цели обучения в соответствии
с учебной программой
|
9.2.2.1 различать линейные и нелинейные уравнения с двумя переменными;
|
Цели урока
|
Все учащиеся смогут
Узнать, что такое нелинейное уравнение с двумя переменными, научиться решать нелинейное уравнение с двумя переменными, строить графики нелинейных уравнений;
Большинство учащихся смогут
Узнать, что такое нелинейное уравнение с двумя переменными, научиться решать нелинейное уравнение с двумя переменными, строить графики нелинейных уравнений
Некоторые учащиеся смогут
Иметь понятие степени с натуральным показателем и умение выполнять преобразования и вычисления со степенями;
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Психологический настрой. Деление на группы.
Каждый учащийся получает номер от 1 до 4. Учащиеся формируют группы по полученным номерам
В начале урока сделать акценты на: концентрацию внимания учащихся совместно с учащимися определить цели урока, определить «зону ближайшего развития» учащихся
« Крестики-нолики»
Вспомнив цель предыдущего урока, с помощью следующих вопросов подводим учащихся к новой цели обучения:
1 Вопросы.
1. Запишите общий вид линейного уравнения с одной переменной.
2. Запишите общий вид линейного уравнения с двумя переменными.
3. Что называют решением линейного уравнения с двумя переменными?
4. В каких случаях можно получить уравнение, равносильное исходному уравнению?
5. Что значит решить уравнение с двумя переменными?
6. Как решить уравнение с двумя переменными?
|
Обмен в парах информацией, полученной на прошлом уроке (Стратегия 1 минута)
Отвечают на вопросы
|
Комментарий учителя
|
Слайд 1
Слайд 2
|
Середина урока
|
Решить систему. Решение записывается на доске.
Решение. Так как х2 - 2у2 - ху = (х + у)(х-2у), то заметим, что множитель, x + y + 1 ≠ 0 так как в этом случае правая часть второго уравнения системы также обратилась бы в нуль. Следовательно, система равносильна системе
Решим второе уравнение, подставив вместо значения х выражение 2у - 1
(2(2у-1)-у +1)(2у-1+у+1) =6
( 4у - 2 -у + 1)× 3у = 6
(3у-1)× 3у = 6
9у2-3у -2 = 0
у1= 1; у2 = - 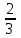
Выразив x из первого уравнения и подставив во второе, получили уравнения для нахождения у. В первое уравнение системы вместо у подставляем найденное значение и находим значения x:
х1 = 1; х2 = - 
Ответ: (1; 1); (-  ; - ; - 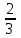 ) )
Уравнения с двумя переменными иx и y имеет вид f(x,y)=φ(x,y), где и f и φ – выражения с переменными и x и y.
Если в уравнении x(x−y)=4 подставить вместо переменной х её значение -1, а вместо у – значение 3, то получится верное равенство: 1⋅(−1−3)=4. Пара (-1; 3) значений переменных х и у является решением уравнения x(x−y)=4.
То есть решением уравнения с двумя переменными называют множество упорядоченных пар значений переменных, образующих это уравнение в верное равенство.
Нелинейные уравнения с двумя переменными решаются также как и линейные уравнения с двумя переменными, с помощью графика. При этом желательно переменную у выразить через х и построить график полученной функции. Все соответствующие координаты точек графика будут являются парами ответов данного уравнения.
Система вида {f1(x,y)=C1
F2(x,y)=C2, называется системой нелинейных уравнений с двумя переменными, если хотя бы одно из уравнений нелинейное. Нелинейные системы не имеют универсального способа решения, поэтому при решении конкретной системы уравнений нужно учитывать особенности заданных уравнений, переходя к равносильным системам.
Две системы называются равносильными, если множества их решений совпадают или обе системы не имеют решений.
Утверждения о равносильности систем уравнений:
если одно из уравнений системы заменить на равносильное уравнение, то получим систему, равносильную исходной;
если одно из уравнений системы заменить суммой каких-либо двух уравнений данной системы, то получим систему, равносильную исходной;
если одно из уравнений системы выражает зависимость какой-либо переменной, например x, через другие переменные, то, заменив в каждом уравнении системы переменную x на ее выражение через другие переменные, получим систему, равносильную исходной.
Рассмотрим некоторые методы решения нелинейных систем уравнений.
Провести самостоятельную работу по паре , которая носит дифференцированный характер, с последующей взаимопроверкой и консультацией
Самостоятельная работа дифференцированная
Задание.1
1. Постройте график уравнения 3х – у = 6.
2. Найдите точки пересечения графика уравнения 2х+ у = 4 с координатными осями без построения графика:
3. График уравнения ах + 5у = 10 проходит через точку А(5;-1). Найдите значение коэффициента а.
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Определяет решение нелинейного уравнения с двумя переменными
|
1
|
Проверяет, что пара чисел является решением нелинейного уравнения с двумя переменными
|
1
|
Выполняет действия с числами
|
1
|
Выбирает пары чисел, являющиеся решением уравнения
|
1
|
Решает системы уравнений способом сложения
|
2
|
Выполняет алгебраические преобразования уравнений
|
1
|
Использует способ сложения
|
1
|
Находит значение переменной х
|
1
|
Находит значение переменной у
|
1
|
Записывает решение системы уравнений
|
1
|
Заполните таблицу, работа выполняется в парах (пары перемешать)
Уравнение
|
Степень
|
Выражаем у через х
|
Данной формулой задается …
функция
|
Графиком является
…
|
3х+2у=6
|
|
|
|
|
у-х2=0
|
|
|
|
|
2х+у=0
|
|
|
|
|
ху=4
|
|
|
|
|
ФО оценивание по дескрипторам
Дескрипторы
|
- отвечает на вопросы;
- правильно указывают данные ответы;
- делает выводы по результатам задании .
|
Индивидуальная работа
Постройте график уравнения у-0,2х=5, выясните, проходит ли этот график через точку А(100;113)
Постройте графики уравнений
а) х2+у2=36
б) ху=12
Решите систему уравнений
 
а) х+2у=13 б) у-2х=2
ху=15 5х2-у=1
Критерии оценивания:
Учащийся достиг цели обучения, если…
- Представляет информацию в виде иллюстраций, комиксов или другом виде в т.ч. с использованием ИКТ
- допускает не более 2-х ошибок
- оригинальность выполнения работы
|
Выполняют краткую запись в тетрадях
Выполняют задание
Пары меняются составом и работают над данным заданием
Работают индивидуально
|
взаимооценивание
по дескрипторам
Прием «Карусель»
по дескрипторам
смайлики
|
Слайд 3
Слайд 4
Приложение 1
Слайд 5
Приложение 2
Слайд 6
Приложение 3
|
Конец урока
|
Рефлексия. Заполни дискуссионную карту.
«V»
|
«W»
|
«| »
|
«+»
|
«0»
|
ответил по просьбе учителя, но ответ не правильный
|
ответил по просьбе учителя, ответ правильный
|
ответил по своей инициативе, но ответ не правильный
|
ответил по своей инициативе, ответ правильный
|
не ответил
|
|
Заполнят карту.
Подводят итоги урока
|
аплодисменты
|
Приложение 4
|
Домашнее задание
|
Номер из учебника
|
Записывают в дневник домашнее задание
|
Комментарий учителя
|
| |
|
|
 Скачать 53.09 Kb.
Скачать 53.09 Kb.