Введение
На сегодняшний день изображения занимают значительное место в обмене информацией. В связи с необходимостью защиты авторских прав данных файлов и другой мультимедийной информации были разработаны цифровые водяные знаки (watermarks). Цифровой водяной знак должен отвечать следующим требованиям:
– незаметность для пользователей;
– индивидуальность алгоритма нанесения;
– возможность для автора обнаружить несанкционированное использование файла;
– невозможность удаления неуполномоченными лицами;
– устойчивость к изменениям носителя-контейнера (к изменению его формата и размеров, к масштабированию, сжатию, повороту, фильтрации, введению спецэффектов, монтажу, аналоговым и цифровым преобразованиям).
Поиск алгоритма создания цифрового водяного знака в большей степени отвечающего всем предложенным критериям является первоочередной задачей инженеров для защиты авторских прав в сети Интернет. Целью данной работы является рассмотрение метода внедрение цифрового водяного знака в изображение, путём деления ЦВЗ и изображения на равное количество частей, и встраивания в каждую часть изображения соответствующей части ЦВЗ.
Алгоритм внедрения цифрового водяного знака
Рис. 1
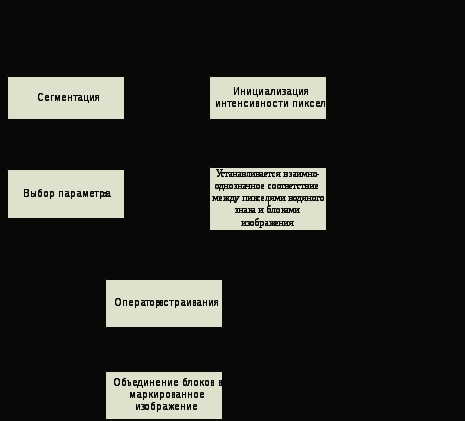
2. Инициализация начальных параметров
2.1 Изображение
Изображение, в которое будет встраиваться цифровой водяной знак, представим как 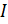 , с размерами MxN. , с размерами MxN.
I = 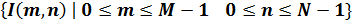 (1) (1)
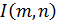 – пиксели изображения; – пиксели изображения; 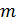 – положение пикселя по горизонтали; – положение пикселя по горизонтали; 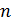 – положение пикселя по вертикали; – положение пикселя по вертикали; 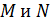 – ширина и высота изображения в пикселях соответственно; – ширина и высота изображения в пикселях соответственно;
2.2 Цифровой водяной знак
В качестве цифрового водяного знака возьмём изображение, c размерами KxL:
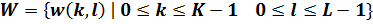 (2) (2)
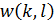 – пиксели изображения; – пиксели изображения; 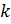 – положение пикселя по горизонтали; – положение пикселя по горизонтали; 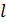 – положение пикселя по вертикали; – положение пикселя по вертикали; 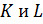 – ширина и высота водяного знака в пикселях соответственно; – ширина и высота водяного знака в пикселях соответственно;
2.3 Параметры необходимые знать для внедрения водяного знака:
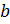 – интенсивность пикселя водяного знака; – интенсивность пикселя водяного знака; 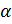 – константа, определяющая степень (силу) встраивания водяного знака. – константа, определяющая степень (силу) встраивания водяного знака.
3. Внедрение цифрового знака в изображение
Разбиение изображения на блоки, количество которых равно количеству пикселей водяного знака.
При разбиении изображения получается KL блоков с размерами
U = M/K,
V = N/ L.
Устанавливается взаимно-однозначное соответствие между пикселями водяного знака и полученными блоками, используя ключ.
Встраивание пикселя водяного знака в блок изображения.
Рассмотрим случай, когда K = L = 1, т.е. изображение состоит из одного блока, а водяной знак состоит из одного пикселя с интенсивностью b11. Пусть M,N > 1, тогда имеем некоторую избыточную возможность помещения водяного знака в пиксели изображения, и при разумном подборе оператора встраивания можно повысить устойчивость всей процедуры защиты информации в целом. Предлагается оператор встраивания, основанный на следующей формуле:
Iw(m,n) = (1-б) * I(m,n) + бb11 (3)
Iw(m,n) – маркированное изображение; b11 – интенсивность пикселя водяного знака; I(m,n) – исходное изображение; α > 0 – константа, определяющая степень (силу) встраивания водяного знака;
Выбор параметра б.
При отсутствии случайных атак, степень (среднеквадратического) искажения изображения вследствие встраивания водяного знака определяется по формуле:
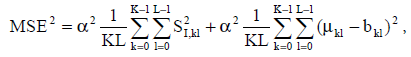 (4) (4)
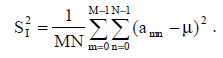 (5) (5)
MSE2 – степень искажения изображения; α > 0 – константа, определяющая степень (силу) встраивания водяного знака; 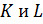 – ширина и высота водяного знака в пикселях соответственно; – ширина и высота водяного знака в пикселях соответственно; 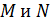 – ширина и высота изображения в пикселях соответственно; µ - средняя интенсивность пикселей изображения; – ширина и высота изображения в пикселях соответственно; µ - средняя интенсивность пикселей изображения; 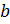 – интенсивность пикселей водяного знака; что показывает степень искажений, вносимых самой процедурой встраивания водяного знака. Выражение (4) позволяет ещё до встраивания водяного знака определить степень ожидаемых искажений и контролировать ее путем надлежащего выбора параметра б. – интенсивность пикселей водяного знака; что показывает степень искажений, вносимых самой процедурой встраивания водяного знака. Выражение (4) позволяет ещё до встраивания водяного знака определить степень ожидаемых искажений и контролировать ее путем надлежащего выбора параметра б.
Объединение блоков в маркированное изображение.
4. Алгоритм извлечения цифрового водяного знака из изображения
Используя ключ, определяем взаимнооднозначное соответствие между байтами водяного знака и блоками изображения.
Разбиваем изображение на блоки.
Извлечение ЦВЗ из блока в отсутствии каких-либо атак производится по формуле:
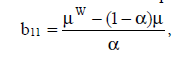 (6) (6)
где:
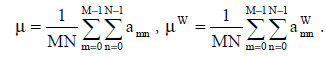 (7) (7)
b11 – интенсивность пикселя водяного знака; µ - средняя интенсивность пикселей изображения; α > 0 – константа, определяющая степень (силу) встраивания водяного знака; 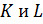 – ширина и высота водяного знака в пикселях соответственно; – ширина и высота водяного знака в пикселях соответственно; 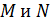 – ширина и высота изображения в пикселях соответственно. – ширина и высота изображения в пикселях соответственно.
Задача извлечения ЦВЗ сводится к оцениванию параметра b11 по выборке:
Iw(m,n) = (1-б) * I(m,n) + бb11.
цифровой байт несанкционированный
Восстанавливаем водяной знак.
Восстанавливаем исходное изображение.
5. Алгоритм извлечения водяного знака из изображения, подверженного атаке
Аддитивная модель изменения значений пикселей после атаки:
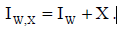 (8) (8)
Предполагается, что значения x(m,n) случайной величины X накладываются на пикселы независимо и с одинаковой функцией распределения. Тогда:
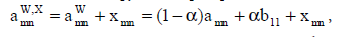 (9) (9)
и задача извлечения ЦВЗ сводится к оцениванию параметра b11 по выборке aw,x(m,n) , m = 0,1,...,M-1; n = 0,1,...,N -1.
Можно показать, что оценка наименьших квадратов при этом имеет вид:
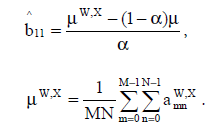 (10) (10)
Если принять, что случайная величина X распределена со средним ноль и с дисперсией 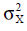 , то дисперсия оценки (10) будет равна: , то дисперсия оценки (10) будет равна:
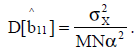 (11) (11)
Формула (11) характеризует помехоустойчивость предложенного метода встраивания ЦВЗ к атакам со случайными характеристиками.
Представляет интерес исследование степени искажения изображения вследствие встраивания в него ЦВЗ и воздействия атаки X. Для этого вычислим среднеквадратическое отклонение интенсивностей пикселов изображений I и Iw,x.
Можно показать, что:
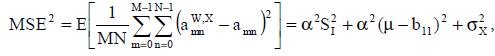 (12) (12)
где:
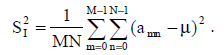 (13) (13)
Первое слагаемое выражения (12) является показателем рассеяния интенсивностей пикселов изображения I относительно средней интенсивности. Чем больше этот показатель, тем больше различаются атакованное изображение со встроенным ЦВЗ и изображение-контейнер. Этот факт показывает принципиальное различие предложенного алгоритма от адаптивного алгоритма, в котором высокие значения этого же показателя позволяют более успешно встраивать ЦВЗ.
Второе слагаемое в (12) является мерой отклонения интенсивности встраиваемого ЦВЗ от средней интенсивности пикселов изображения. Естественно, большие отклонения приведут к соответственно большим отклонениям между изображениями I и Iw,x . При этом большое значение имеет также параметр a. Третье слагаемое показывает непосредственное влияние рассеяния самой случайной величины X на процедуру встраивания.
6. Результаты моделирования и численных расчетов
Рассмотрим численные примеры встраивания и извлечения ЦВЗ в изображение и оценивания помехоустойчивости предложенной процедуры. Расчеты удобно проводить в логарифмическом масштабе на основе расчета PSNR.
Для эксперимента выбрано изображение маммограммы пациента N, имеющее размеры 256 x 256 пикселов и ЦВЗ с фотографией пациента c размерами 64 x 64. Защита информации состоит во встраивании фотографии пациента в изображение маммограммы. Встраивание ЦВЗ проведено при a = 0,07.
Визуальный анализ изображения-оригинала I и изображения со встроенным ЦВЗ W I никаких заметных различий в них не обнаружил. Значение PSNR = 31,6 дБ также свидетельствует о достаточной близости этих изображений по среднеквадратическому критерию.
Исследование устойчивости предложенного алгоритма проведено для двух типов атак.
1. Устойчивость к случайным атакам, проявляемым в соответствии с моделью (10) с использованием численного моделирования в предположении, что случайная величина X распределена как 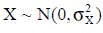 для различных значений дисперсии для различных значений дисперсии 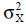 . .
PSNR (дБ) между изображениями I и Iw,x , извлеченные ЦВЗ и PSNR между встроенным и извлеченным ЦВЗ при различных значениях 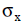
Таблица 1

В табл. 1 приведены полученные результаты для одной реализации случайной величины X . Видно, что с увеличением 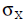 ухудшается качество извлеченного ЦВЗ, оставаясь, впрочем, на уровне, достаточном для узнавания образа пациента вплоть до значения ухудшается качество извлеченного ЦВЗ, оставаясь, впрочем, на уровне, достаточном для узнавания образа пациента вплоть до значения 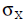 =6. Качество же изображения со встроенным ЦВЗ остается в районе 30 дБ, что никак не отражается на диагностической ценности деталей данной маммограммы. =6. Качество же изображения со встроенным ЦВЗ остается в районе 30 дБ, что никак не отражается на диагностической ценности деталей данной маммограммы.
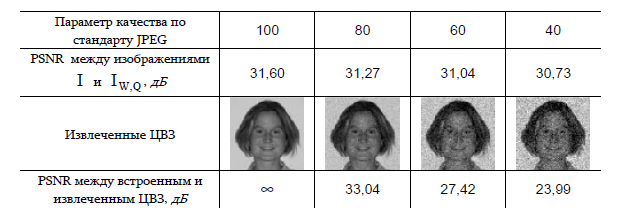
2. Устойчивость к сжатию по стандарту JPEG. В табл. 2 приведены результаты по исследованию устойчивости предложенной процедуры к атакам в виде сжатия при помощи стандарта JPEG для различных значений параметра качества Q. Эксперименты проводились на тех же изображении-контейнере и ЦВЗ.
Выводы, которые можно сделать из данных табл. 2, во многом схожи с выводами, сделанными относительно табл. 1. Отметим, однако, неожиданно высокую устойчивость предложенной процедуры к достаточно сильному сжатию изображений: ведь при параметре качества, равном всего 40, размер сжатого JPEG-файла для рассматриваемого изображения составляет около 6% от исходного при сохранении качества на уровне около 31 дБ и вполне различимом образе пациента по извлеченному ЦВЗ.
PSNR (дБ) между изображениями I и I(w,x) , извлеченные ЦВЗ и PSNR между встроенным и извлеченным ЦВЗ при различных значениях параметра качества Q.
Таблица 2
7. Пример реализации алгоритма в среде Matlab
Исходный код программы в приложении А
В данном алгоритме мы производим операции с изображением. Внедряем в исходное изображение водяной знак. Извлекаем из маркированного изображения водяной знак, и рассчитываем качество внедрения (PSNR).
PSNR полученного изображения, при выборе коэффициента б = 0.07, составляет 28dB. PSNR извлеченного водяного знака, при коэффициенте б = 0.07, составляет 70dB.
Гистограмма оригинального изображения имеет небольшие отличия от гистограммы маркированного изображения (б = 0.07), что говорит о хорошем качестве встраивания, но при б = 0.1, гистограммы сильно различаются.
PSNR полученного изображения, при выборе коэффициента б = 0.1, составляет 25dB. PSNR извлеченного водяного знака, при коэффициенте б = 0.1, составляет 73dB.
При увеличении коэффициента б, снижается качество маркированного изображение, но повышается качество извлеченного водяного знака. Поэтому перед началом внедрения ЦВЗ в изображение необходимо рассчитать оптимальный коэффициент встраивания б.
8. Пример внедрения водяного знака (qr-кода) в изображение
Исходный код программы в приложении B.
В данном алгоритме мы производим операции с изображением. Внедряем в исходное изображение qr код. Извлекаем из маркированного изображения водяной знак, и рассчитываем качество внедрения (PSNR).
PSNR полученного изображения, при выборе коэффициента б = 0.07, составляет 28dB. PSNR извлеченного водяного знака, при коэффициенте б = 0.07, составляет 277dB.
Гистограмма оригинального изображения имеет небольшие отличия от гистограммы маркированного изображения (б = 0.07), что говорит о хорошем качестве встраивания, но при б = 0.1, гистограммы сильно различаются.
PSNR полученного изображения, при выборе коэффициента б = 0.1, составляет 26dB. PSNR извлеченного водяного знака, при коэффициенте б = 0.1, составляет 282dB.
При увеличении коэффициента б, снижается качество маркированного изображение, но повышается качество извлеченного водяного знака. Поэтому перед началом внедрения ЦВЗ в изображение необходимо рассчитать оптимальный коэффициент встраивания б.
Заключение
Предложен алгоритм, основанный на встраивании цифровых водяных знаков (ЦВЗ) в пространственную область изображения и извлечения из него ЦВЗ. Получены аналитические выражения для среднеквадратической ошибки, вызываемой процедурой встраивания при наличии случайной атаки, зависящие от характеристик изображений, процедуры встраивания и атаки. Методом моделирования исследовалась устойчивость предложенного алгоритма к случайной атаке, а также к сжатию изображения по стандарту JPEG.
Список использованной литературы
1. Cox J., Miller M. L. and Bloom J.A. Digital Watermarking. - Morgan Kaufmann, 2001.
2. Hartung M., Kutter M. Multimedia Watermarking Techniques //Proceedings of the IEEE. – July, 1999. - Vol. 87, № 7. - P. 1079-1086.
3. Anand D., Niranjan U.C. Watermarking Medical Images with Patient Information //Proc. IEEE/EMSB Conference. - Hong Kong, China, Oct. 1998. – P. 703-706.
4. Асатрян Д.Г., Ланина Н.С. Адаптивный алгоритм встраивания цифровых водяных знаков в изображение //Труды научной годичной конференции Российско-Армянского (Славянского) государственного университета. - Ереван, 2006. - Т.1. - C. 87-90.
5. Podilchuk C I., Zeng W. Image-adaptive watermarking using visual models //IEEE Journal of Selected Areas in Communication. – 1998. - 16(4). – P. 525–539.
6. Chang-Hsing Lee, Yeuan-Kuen Lee. An Adaptive Digital Image Watermarking Technique for Copyright Protection // IEEE Transactions on Consumer Electronics. – 1999. - V. 45, № 4. - P. 1005-1015.
7. Asatryan D.G., Lanina N.S., Shahverdyan H.S. Adaptive Robust Algorithm for Digital Watermarking of Medical Images //Proc. of 6th Int. Conf. on Computer Science and Information Technologies - CSIT'2007. - Yerevan, 2007. - P. 161-164.
Приложения
Приложение А
clear;
clc
img=imread('F:\works\kursa4\lena.png');
img=imresize(img,[512,512]);
img=rgb2gray(img);
[M,N]=size(img);
img=double(img);
[Uimg,Simg,Vimg]=svd(img);
Simg_temp=Simg;
img_wat=imread('F:\works\kursa4\shevel.png');
img_wat=imresize(img_wat,[512,512]);
img_wat=rgb2gray(img_wat);
alfa= input('The alfa Value = ');
[x,y]=size(img_wat);
img_wat=double(img_wat);
for i=1:x
for j=1:y
Simg(i,j)=(1-alfa)*Simg(i,j) + alfa * img_wat(i,j);
end
end
% SVD for Simg (SM)
[U_SHL_w,S_SHL_w,V_SHL_w]=svd(Simg);
Wimg =Uimg* S_SHL_w * Vimg';
figure(1)
imhist(uint8(img));
title('Histogramma of original image')
figure(2)
imshow(uint8(img));
title('The Original Image')
figure(3)
imshow(uint8(img_wat));
title('The Watermark ')
figure(4)
imshow(uint8(Wimg));
title('The Watermarked Image')
figure(5)
imhist(uint8(Wimg));
title('Histogramma of watermarking image')
%%%%%%%%%%%%%%%%%%%%%%%%%%%
%calculate image quality degradation after inserting watermark
%%%%%%%%%%%%%%%%%%%%%%%%%%%
mse=mean(squeeze(sum(sum((double(img)-double(Wimg)).2))/(M*N)));
PSNR=10*log10(2552./mse);
msg=sprintf('\n\n-------------------------\nWatermark by SVD PSNR=%fdB\n-----------------------------\n\n', PSNR);
disp(msg);
%--------------------------------------------------------------------------
% %% Extraction Part
% -------------------------------------------------------------------------
[UWimg,SWimg,VWimg]=svd(Wimg);
D_1=U_SHL_w * SWimg * V_SHL_w';
for i=1:x
for j=1:y
Watermark(i,j)= (D_1(i,j) - Simg_temp(i,j)*(1-alfa))/alfa;
end
end
figure(6)
imshow(uint8(Watermark));
title('The Extracted Watermark ')
mse=mean(squeeze(sum(sum((double(img_wat)-(Watermark)).2))/(M*N)));
PSNR=10*log10(2552./mse);
msg=sprintf('\n\n-------------------------\nWatermark by SVD PSNR=%fdB\n-----------------------------\n\n', PSNR);
Приложение B
clear;
clc
img=imread('F:\works\kursa4\lena.png');
img=imresize(img,[512,512]);
img=rgb2gray(img);
[M,N]=size(img);
img=double(img);
[Uimg,Simg,Vimg]=svd(img);
Simg_temp=Simg;
% read watermark
img_wat=imread('F:qrkod.png');
img_wat=imresize(img_wat,[512,512]);
alfa= input('The alfa Value = ');
[x,y]=size(img_wat);
img_wat=double(img_wat);
for i=1:x
for j=1:y
Simg(i,j)=(1-alfa)*Simg(i,j) + alfa * img_wat(i,j);
end
end
% SVD for Simg (SM)
[U_SHL_w,S_SHL_w,V_SHL_w]=svd(Simg);
Wimg =Uimg* S_SHL_w * Vimg';
figure(1)
imhist(uint8(img));
title('Histogramma of original image')
figure(2)
imshow(uint8(img));
title('The Original Image')
figure(3)
imshow(img_wat);
title('The Watermark ')
figure(4)
imshow(uint8(Wimg));
title('The Watermarked Image')
figure(5)
imhist(uint8(Wimg));
title('Histogramma of watermarking image')
%%%%%%%%%%%%%%%%%%%%%%%%%%%
%calculate image quality degradation after inserting watermark
%%%%%%%%%%%%%%%%%%%%%%%%%%%
mse=mean(squeeze(sum(sum((double(img)-double(Wimg)).2))/(M*N)));
PSNR=10*log10(2552./mse);
msg=sprintf('\n\n-------------------------\nWatermark by SVD PSNR=%fdB\n-----------------------------\n\n', PSNR);
disp(msg);
%--------------------------------------------------------------------------
% %% Extraction Part
% -------------------------------------------------------------------------
[UWimg,SWimg,VWimg]=svd(Wimg);
D_1=U_SHL_w * SWimg * V_SHL_w';
for i=1:x
for j=1:y
Watermark(i,j)= (D_1(i,j) - Simg_temp(i,j)*(1-alfa))/alfa;
end
end
figure(6)
imshow(Watermark);
title('The Extracted Watermark ')
mse=mean(squeeze(sum(sum((double(img_wat)-(Watermark)).2))/(M*N)));
PSNR=10*log10(2552./mse);
msg=sprintf('\n\n-------------------------\nWatermark by SVD PSNR=%fdB\n-----------------------------\n\n', PSNR) |
 Скачать 3.12 Mb.
Скачать 3.12 Mb.

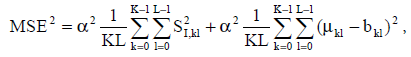 (4)
(4)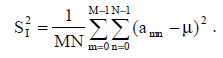 (5)
(5)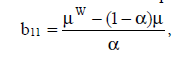 (6)
(6)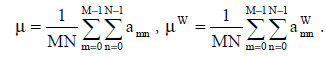 (7)
(7)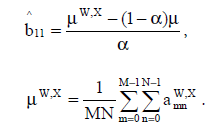 (10)
(10)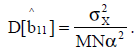 (11)
(11)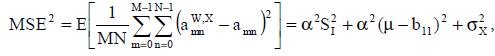 (12)
(12)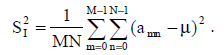 (13)
(13)
