|
|
Диплом. ГОТОВЫЙ ДИПЛОМ Адамова Гульжан. Незначительное влияние параметров линии передачи на характеристики каналов
Характеристики кабеля ОМЗКГМ-10-01-0,22-24(7,0)
Параметр
|
Значение
|
Оптическое волокно
|
Одномодовое
|
Количество ОВ
|
24
|
Диаметр кабеля, мм
|
12,9…20,8
|
Масса, кг/км
|
258…859
|
Коэффициент затухания
на длине волны 1,55 мкм, дБ/км
|
0,22, не более
|
Хроматическая дисперсия на длине волны 1,55 мкм, пс/нм∙км
|
18, не более
|
Допустимое растягивающее усилие, кН
|
7,0
|
Допустимое раздавливающее усилие,кН/см
|
0,6
|
Срок службы, лет
|
25, не менее
|
Строительная длина, м
|
5000, не более
|
2.4 Расчет оптических и передаточных параметров оптического кабеля
Основным элементом оптического кабеля является волоконный
световод – круглый стержень из оптически прозрачного диэлектрика. Оптические волноводы из-за малых размеров поперечного сечения обычно называют волоконными световодами или оптическими волокнами (ОВ).
Оптическое волокно состоит из сердцевины, по которой распространяются световые волны и оболочки. Сердцевина служит для передачи световых волн. Назначение оболочки – создание лучших условий отражения на границе «сердцевина-оболочка» и защита от излучения энергии в окружающее пространство. С целью повышения прочности и тем самым надежности волокна поверх оболочки накладывается первичное защитное упрочняющее покрытие.
Для передачи электромагнитной энергии по световоду используется явление полного внутреннего отражения на границе раздела двух сред. Эффект полного внутреннего отражения реализуется в световодах при соблюдении условия:
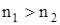 (2.9) (2.9)
где 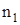 - показатель преломления сердцевины оптического волокна; - показатель преломления сердцевины оптического волокна; 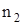 - показателя преломления оболочки оптического волокна. - показателя преломления оболочки оптического волокна.
На рисунке 2.4 изображено распространение лучей в оптическом волокне.
Распространение лучей в оптическом волокне
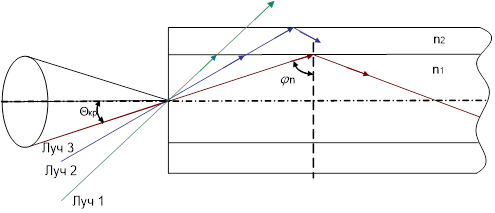
Рисунок 2.4
Луч полностью отражается на границе «сердцевина-оболочка» и остаётся внутри сердцевины (луч 3), когда угол падения ( ) меньше критического угла, который определяется соотношением: ) меньше критического угла, который определяется соотношением:
 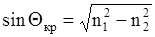 (2.10) (2.10)
Величину 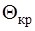 называют апертурным углом. называют апертурным углом.
Апертура - это угол между оптической осью и одной из образующих светового конуса, падающего в торец волоконного световода, при котором выполняется условие полного внутреннего отражения.
Наряду с понятием «угловая апертура» принято использовать понятие «числовая апертура» (Numerical Aperture).
Числовая апертура представляет собой синус максимального угла падения лучей на торец световода, при котором луч в световоде падает на границу «сердцевина-оболочка» под критическим углом 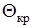 . .
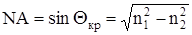 (2.11) (2.11)
Числовая апертура равна:
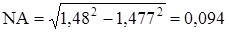
Нормированная, или характеристическая, частота – один из важнейших обобщающих параметров, который связывает структурные параметры оптического волокна и длину световой волны, распространяемой в волокне. По значению нормированной частоты можно судить о режиме работы оптического волокна. При 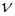 < 2,405 – режим работы оптического волокна – одномодовый. < 2,405 – режим работы оптического волокна – одномодовый.
При 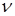 > 2,405 – режим работы оптического волокна – многомодовый. > 2,405 – режим работы оптического волокна – многомодовый.
Нормированная частота определяется по формуле:
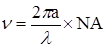 , (2.12) , (2.12)
где а – радиус сердцевины волокна, м; λ – рабочая длина волны, м; NA – числовая апертура. Нормированная частота равна:
 = 1,90 = 1,90
Из полученного результата 1,90 < 2,405 следует, что режим работы по оптическому волокну – одномодовый. Достоинством одномодовых систем является весьма широкий диапазон частот и большая пропускная способность.
Определяется длина волны и частоты, для критического режима, когда поле выходит за пределы оптического волокна и энергия по световоду не распространяется. Критическая длина волны определяется по формуле:
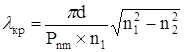 (2.13) (2.13)
где d – диаметр сердцевины оптического волокна, м; Рnm – 2,405 значение корня функции Бесселя; n1 и n2 – показатели преломления сердцевины и оболочки.
Критическая длина волны равна:
 = 0,83 мкм = 0,83 мкм
Критическая частота определяется по формуле:
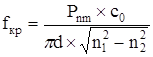 (2.14) (2.14)
где Pnm – значение корня функции Бесселя; с0 – скорость света, м/с; d – диаметр сердцевины, м; n1 и n2 – показатели преломления сердцевины и оболочки.
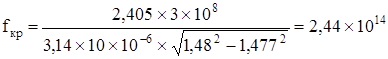
2.5 Расчет затухания, дисперсии
Затухание и потери являются параметрами, определяющими дальность передачи по оптическому кабелю и его эффективность.
Затухание световодных трактов оптических кабелей (a), характеризуется собственными потерями в световодах (ac) и дополнительными потерями, обусловленными деформацией и изгибами световодов при наложении покрытий и защитной оболочки при изготовлении кабеля (aк). Суммарное затухание равно:
a=aс +aк (2.15)
Собственные потери волоконных световодов состоят в первую очередь из потерь поглощения (aп) и потерь рассеяния (aр).
Потери на поглощение существенно зависят от чистоты материала и при наличии посторонних примесей (aпр) могут быть значительными.
Собственное затухание рассчитывается по формуле:
aс =aп +aр (2.16)
Затухание в результате поглощения (aп) связано с потерями на диэлектрическую поляризацию, оно линейно растет с частотой, зависит от свойств материала световода (tgδ) и определяется по формуле:
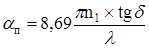 , (2.17) , (2.17)
где n1 – показатель преломления сердцевины; tgδ = 1∙10-12 – тангенс диэлектрических потерь материала сердцевины оптического волокна; λ - рабочая длина волны, км.
Затухание поглощения равно:
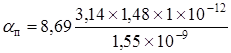 = 0,0261 дБ/км = 0,0261 дБ/км
Затухание вследствие рассеяния (aр ) обусловлено неоднородностями материала ОВ, размеры которых меньше длины волны, и тепловой флуктуацией показателя преломления.
Затухание рассеяния определяется выражением:
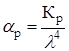 (2.18) (2.18)
где Кр – коэффициент рассеяния, для кварца равен 0,6 мкм4.
Затухание рассеяния равно:
 = 0,104 дБ/км = 0,104 дБ/км
Потери на рассеяние определяют нижний предел потерь оптического волокна. В результате, собственные потери мощности в ОВ составят:
aс = 0,0261 + 0,104 = 0,130 дБ/км
Дополнительные потери в оптических кабелях (aк) обусловлены деформацией оптических волокон в процессе изготовления кабеля - скруткой, изгибами волокон и так далее.
В общем случае дополнительные потери определяются, как:
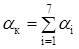 (2.19) (2.19)
В процессе изготовления волокна их классифицируют по следующим семи составляющим:
a1 – возникает вследствие приложения к оптическое-волокно (ОВ) термомеханических воздействий в процессе изготовления кабеля;
a2 – вследствие температурной зависимости коэффициента преломления материала ОВ;
a3 – вызывается микроизгибами ОВ;
a4 – возникает вследствие нарушения прямолинейности ОВ (скрутка);
a5 – возникает вследствие кручения ОВ относительно его оси;
a6 – возникает вследствие неравномерности покрытия ОВ;
a7 – возникает вследствие потерь в защитной оболочке ОВ.
При соблюдении норм технологического процесса изготовления
доминируют потери на микроизгибы.
Потери на микроизгибы и потери в защитных оболочках сравнительно невелики и составляют 0,1 дБ/км.
Расчетное суммарное затухание кабеля равно:
a = 0,130 + 0,1 = 0,23 дБ/км
При прохождении импульсных сигналов по световоду изменяется не только амплитуда импульсов, но и их форма – импульсы уширяются.
Это явление называется дисперсией (τ).
Дисперсия – это рассеивание во времени спектральных или модовых составляющих оптического сигнала, которое приводит к увеличению длительности импульса оптического излучения при распространении его по ОВ, рисунок 2.6.
Модовая (межмодовая) дисперсия обусловлена наличием большого числа мод, каждая из которых распространяется со своей скоростью, и имеет место только в многомодовом волокне.
Затухание световодных трактов оптических кабелей (a), характеризуется собственными потерями в световодах (ac) и дополнительными потерями, обусловленными деформацией и изгибами световодов при наложении покрытий и защитной оболочки при изготовлении кабеля (aк).
Искажение формы импульсов вследствие дисперсии

Рисунок 2.6
Полная классификация составляющих дисперсии оптического волокна приведена на рисунке 2.7.
Модовая (межмодовая) дисперсия обусловлена наличием большого числа мод, каждая из которых распространяется со своей скоростью, и имеет место только в многомодовом волокне.
Основной причиной возникновения хроматической (частотной) дисперсии является некогерентность источников излучения, реально работающих в спектре длин волн. Хроматическая дисперсия складывается из волноводной (внутримодовой) (τвв), материальной (τмат) и профильной (τпр):
τхр = τмат + τвв + τпр (2.20)
Волноводная (внутримодовая) дисперсия обусловлена процессами внутри моды. Она характеризуется направляющими свойствами сердцевины ОВ, а именно: зависимостью групповой скорости моды от длины волны оптического излучения, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра.
Материальная дисперсия обусловлена зависимостью показателя
преломления сердцевины и оболочки от длины волны оптического излучения.
Классификация составляющих дисперсии оптического волокна
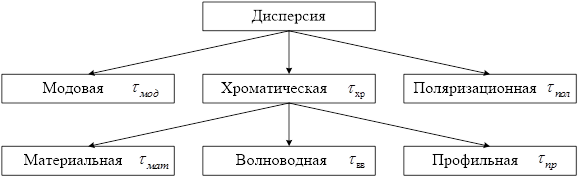
Рисунок 2.7
К основным причинам возникновения профильной дисперсии относятся поперечные и малые продольные отклонения геометрических размеров и формы волокна. Они могут возникать в процессе изготовления ОВ, строительства и эксплуатации ВОЛC.
Материальную, волноводную, профильную дисперсии определим по формулам:
τмат =∆λ М(λ), (2.21)
τвв =∆λ В(λ), (2.22)
τпр =∆λ П(λ), (2.23)
где ∆λ = 0,5 ширина спектра источника излучения, нм (для выбранной системы передачи); М(λ)=-18 пс/нм∙км удельная дисперсия материала; В(λ)=12 пс/нм∙км удельная волноводная дисперсия; П(λ)=5,5 пс/нм∙км удельная профильная дисперсия.
По формулам (2.21; 2.22; 2.23) рассчитается материальная, волноводная, профильная дисперсия:
τмат =0,5 ∙ (-18)=-9 пс/км,
τвв = 0,5 ∙ 12=6 пс/км,
τпр =0,5 ∙ 5,5=2,75 пс/км
Поляризационная модовая дисперсия возникает вследствие различной скорости распространения двух взаимно перпендикулярных поляризационных составляющих моды. Главная физическая причина появления PMD – не круглость профиля сердцевины одномодового волокна. PMD типового волокна, как правило составляет от 0,5 до 0,2 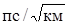 . .
Поляризационная модовая дисперсия начинает сказываться только при скорости передачи выше 2,5 Гбит/с, поэтому при расчете ее не учитываем.
Результирующая хроматическая дисперсия равна:
τхр = -9 + 6 + 2,75 = - 0,5 пс/км
Полоса частот DF, пропускаемая световодом определяет объем информации, который можно передать по ОВ. Так как импульс на приеме приходит искаженным (вследствие различия скоростей распространения в ОВ отдельных частотных составляющих сигнала), то происходит ограничение полосы пропускания сигнала. Дисперсия (t) связана с полосой пропускания следующим соотношением:
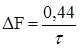 (2.24) (2.24)
Определяется полоса пропускания волоконного световода:
 = 880 ГГц∙км = 880 ГГц∙км
2.6 Расчет количества и помехоустойчивости линейных регенераторов
Характеристики линейного регенератора:
 , (2.25) , (2.25)
где a [дБ/км], L - затухание и длина ОВ, P ПОМ, P min – пиковая мощность световых импульсов на выходе ПОМ и чувствительность ПРОМ соответственно.
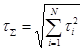 (2.26) (2.26)
где τ i– быстродействие отдельных компонент ВОСП; 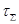 - общее быстродействие системы. - общее быстродействие системы.
В случае NRZ – кода допустимое время нарастания и спада 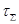 может достигать 70% от периода, т.е.: может достигать 70% от периода, т.е.:
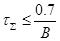 , (2.27) , (2.27)
где B – битовая скорость. Для бифазных кодов:
 , (2.28) , (2.28)
Составляющими суммы в (2) являются:
быстродействие ПОМ и его контроллера τпом;
быстродействие ПРОМ τпром; - быстродействие ОК:
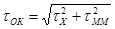 ; ; 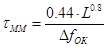 , (2.29) , (2.29)
где D - коэффициент хроматической дисперсии ОВ; 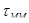 - уширение оптического сигнала, связанное с межмодовой дисперсией в многомодовом ОВ; - уширение оптического сигнала, связанное с межмодовой дисперсией в многомодовом ОВ; 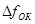 - полоса частот ОВ длиной 1км., которая является справочной величиной. - полоса частот ОВ длиной 1км., которая является справочной величиной.
В условиях, когда чувствительность РЛ определяется тепловым шумом с гауссовой статистикой его коэффициент битовыхошибок p ошопределяется формулой:
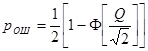 , (2.30) , (2.30)
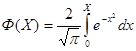 , (2.31) , (2.31)
где Ф (х)- табулированная функция ошибок:
Распространенная аппроксимация функции ошибок:
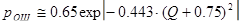 , (2.32) , (2.32)
Величина p ошполностью определяется с помощью Q -факторомпомехоустойчивости ЦСП:
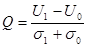 , (2.33) , (2.33)
где, U 1, U 0 - средние уровни напряжений на выходе фотоприемника
на тактовых интервалах (ТИ) длительностью 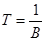 при передаче 1 и 0 соответственно; s1 и s0 - среднеквадратичные уровни шумовых напряжений на указанных ТИ. при передаче 1 и 0 соответственно; s1 и s0 - среднеквадратичные уровни шумовых напряжений на указанных ТИ.
Блок схема линейного регенератора (РЛ)
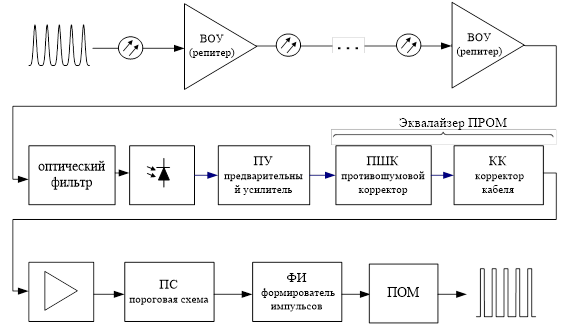
Рисунок 2.7
Выражение(2.33) справедливо, если пороговый уровень U пор решающего устройства ПРОМ установлен равным:
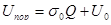 , (2.34) , (2.34)
Параметры U 1 , U 0, s1 и s0 в выражении для Q-фактора шумящего ПУ можно выразить через соотношение чисел сигнальных и шумовых фотоэлектронов на анализируемом ТИ:
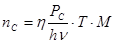 (2.35) (2.35)
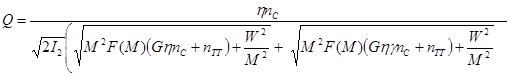 (2.36) (2.36)
где n c - среднее число сигнальных фотоэлектронов на ТИ; 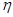 , M , F (M ) - квантовая эффективность коэффициент лавинного умножения и коэффициент , M , F (M ) - квантовая эффективность коэффициент лавинного умножения и коэффициент
шума лавинного ФД; Для p - i - n диода F (M )=1. Для ЛФД:  , где: , где:
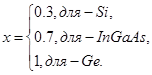 (2.37) (2.37)
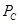 - мощность оптического сигнала; - мощность оптического сигнала; 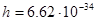 Дж/Гц – постоянная Планка; Дж/Гц – постоянная Планка;
 , (2.38) , (2.38)
Среднее число фотоэлектронов темнового тока 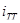 ФД на ТИ, определяющее его дробовой шум; ФД на ТИ, определяющее его дробовой шум; 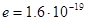 Кл – заряд электрона; T – длительность ТИ. Кл – заряд электрона; T – длительность ТИ.
G - суммарный коэффициент шума репитеров (ВОУ) регенерационного участка длиной L.
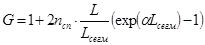 , (2.39) , (2.39)
где 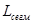 - расстояние между репитерами (ВОУ); - расстояние между репитерами (ВОУ);  - коэффициент затухания сигнала в ОВ; - коэффициент затухания сигнала в ОВ; 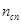 - коэффициент инверсии ВОУ, определяющий его шумовые свойства. - коэффициент инверсии ВОУ, определяющий его шумовые свойства.
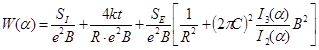 , (2.40) , (2.40)
Безразмерный температурный параметр, определяющий уровень шумов входной цепи и усилителя ПРОМ; t – температура в градусах Кельвина; 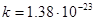 Дж/К – постоянная Больцмана; где Дж/К – постоянная Больцмана; где 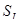 , ,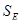 - шумовые параметры транзисторов (см. ниже). - шумовые параметры транзисторов (см. ниже).
Величина R в (2.40) определяет номинал нагрузочного резистора интегрирующего ПУ или сопротивления обратной связи ТИУ. Емкость же C складывается из выходной емкости фотодиода, входной емкости ПУ и емкости монтажа.
В формуле (2.40) коэффициенты I 2,I 3 в, называемые интегралами Персоника, устанавливают соотношение между эффективной шумовойполосой частот ПУ В эфи битовой скоростью B:
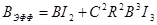 , (2.41) , (2.41)
При этом второе слагаемое (2.41) определяет уширение В эф , связанное с воздействием на помехоустойчивость ПРОМ внутреннего источника шумового напряжения  предварительного усилителя ПРОМ (см.рис.2.9). Коэффициенты I 2,I 3выражается через отношение спектров огибающей оптического сигнала на выходе ( предварительного усилителя ПРОМ (см.рис.2.9). Коэффициенты I 2,I 3выражается через отношение спектров огибающей оптического сигнала на выходе (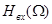 ) и входе ( ) и входе (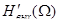 ) ПУ. Аргументом этих зависимостей является безразмерная нормированная частота О=w/T: ) ПУ. Аргументом этих зависимостей является безразмерная нормированная частота О=w/T:
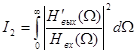 , (2.42) , (2.42)
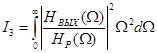 , (2.43) , (2.43)
Спектр 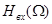 в (2.42),(2.43) определяется формой оптического сигнала на входе ПРОМ Р с (t ), которая чаще всего близка к гауссовой кривой: в (2.42),(2.43) определяется формой оптического сигнала на входе ПРОМ Р с (t ), которая чаще всего близка к гауссовой кривой:
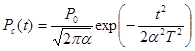 , (2.44) , (2.44)
где a-параметр формы сигнала (см. рис.2.8). Вследствие частотных ограничений АЧХ линейного тракта H (f ) сигнал Р с (t ) на выходе ПРОМ отличается от (2.44). Обычно указанные отклонения используют для минимизации межсимвольной интерференции. Именно этим условием и регламентируется форма АЧХ H (f ) цифрового ПРОМ.
Таким свойством, например, обладает тракт с характеристикой H (f ) вида «приподнятого косинуса»:
 , (2.45) , (2.45)
Которая получила широкое распространение на практике. Для сигналов гауссовой формы и АЧХ вида зависимость интегралов Персоника I 2 ,I 3 от параметра формы гауссового сигнала a изображена на рис.2.9.
Важной характеристикой ЛР является входящий в формулу (2.34) коэффициент уширения сигнала g относительно длительности ТИ. Он описывает дисперсионные искажения цифрового сигнала в ОВ и численно равен доле сигнальных фотоэлектронов рассеянных за пределы «своего» ТИ.
ЗависимостьАЧХ
приподнятого
косинуса
|
Зависимость интеграла Персоника от гаусовского
|
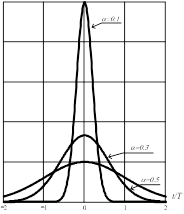
Рисунок 2.8
|
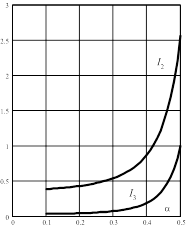
Рисунок 2.9
|
Эта доля и определяет дисперсионное уширение импульса на величину 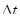 : :
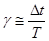 , (2.46) , (2.46)
Для сигналов гауссовой формы рассчитанная по зависимость параметра g от a изображена на рис.2.9.
В одномодовых оптических волокнах (ОВ):
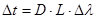 , (2.47) , (2.47)
где 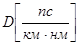 - дисперсионный коэффициент ОВ; L – длина линии связи; - дисперсионный коэффициент ОВ; L – длина линии связи; 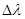 - ширина спектра оптического сигнала. - ширина спектра оптического сигнала.
Значения коэффициента D стандартизировано требованиями МСЭ-Т (ITU-T) и соответствует данным рисунка 2.10. Здесь используются обозначения: DSF (Dispersion Shift Fiber)- ОВ со смещенной дисперсией; NDSF (Non Dispersion Shift Fiber) – стандартное волокно с несмещенной дисперсией; NZ-DSF (Non Zero Dispersion Shift Fiber) – волокно с ненулевой смещенной дисперсией.
Требования на уровень дисперсии в ОВ различного типа
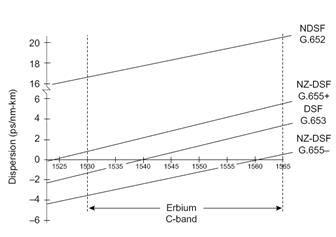
Рисунок 2.10
Для многомодового ОВ со ступенчатым профилем:
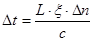 , (2.48) , (2.48)
где 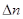 - разность показателей преломления сердцевины - разность показателей преломления сердцевины 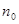 и оболочки и оболочки 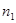 ОВ: ОВ:
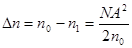 , (2.49) , (2.49)
NA – числовая апертура ОВ; 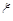 - параметр связи мод (если связи нет, то - параметр связи мод (если связи нет, то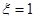 ; полная связь- ; полная связь-  ). ).
Для многомодового градиентного ОВ:
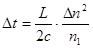 , (2.50) , (2.50)
Теоретическое ограничение на минимальную ширину линии излучения лазера 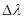 . Если излучение идеального лазера ( . Если излучение идеального лазера (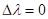 ) модулируется со высокой скоростью B , то линия излучения уширяется на величину: ) модулируется со высокой скоростью B , то линия излучения уширяется на величину:
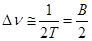
Зависимость коэффициента уширения g от параметра a сигнала гауссовой формы
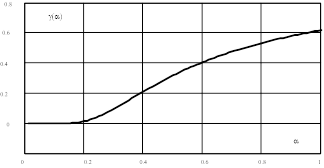
Рисунок 2.11
Откуда, учитывая, что  , получается: , получается:
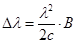 , (2.51) , (2.51)
Из (2.51) следует, что уширение линии излучения, связанное с модуляцией ЛД, при скорости B 10 Гбит/с превышает ширину спектра немодулированного излучения DBF – лазера и этот эффект следует учитывать при расчете МСИ-1. |
|
|
 Скачать 1.04 Mb.
Скачать 1.04 Mb.





 = 1,90
= 1,90 = 0,83 мкм
= 0,83 мкм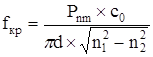 (2.14)
(2.14)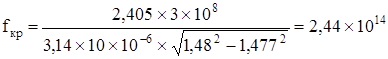
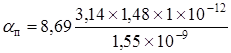 = 0,0261 дБ/км
= 0,0261 дБ/км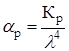 (2.18)
(2.18) = 0,104 дБ/км
= 0,104 дБ/км

 = 880 ГГц∙км
= 880 ГГц∙км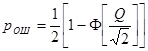 , (2.30)
, (2.30) 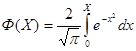 , (2.31)
, (2.31) 
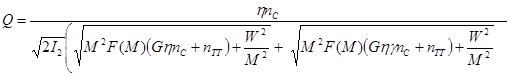 (2.36)
(2.36)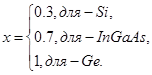 (2.37)
(2.37)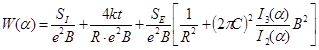 , (2.40)
, (2.40)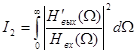 , (2.42)
, (2.42) 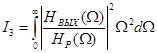 , (2.43)
, (2.43)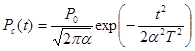 , (2.44)
, (2.44)  , (2.45)
, (2.45)