Нформатика, 10 класс К. Ю. Поляков, Е. А. Ере

• Название: Нформатика, 10 класс К. Ю. Поляков, Е. А. Ере
• Дата: 17.10.2022
• Размер: 0.84 Mb.
• Имя файла: samdo10-3bu.doc
• Тип: Документы; #738727

И
18.10.2022
нформатика, 10 класс К.Ю. Поляков, Е.А. Еремин

3. Логические основы компьютеров

Самостоятельные работы

1. 
   Доказательство логических тождеств

Используя таблицы истинности, докажите или опровергните тождества:

Вариант 1

1) 2) 3)

Вариант 2

1) 2) 3)

Вариант 3

1) 2) 3)

Вариант 4

1) 2) 3)

Вариант 5

1) 2) 3)

Вариант 6

1) 2) 3)

Вариант 7

1) 2)

3)

Вариант 8

1) 2)

3)

Вариант 9

1) 2)

3)

Вариант 10

1) 2)

3)

Ответы:

Вар.	1	2	3	4	5	6	7	8	9	10
1	+	–	–	+	–	+	+	+	+	+
2	+	+	–	–	+	–	–	+	+	–
3	+	+	+	–	+	+	–	+	–	+

2. 
   Синтез логических выражений

Постройте и упростите логические выражения, соответствующие приведённым таблицам истинности. В каждом случае выбирайте наиболее простой способ синтеза. В вашем решении опишите все шаги алгоритма.

Вариант 1

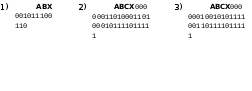
Вариант 2

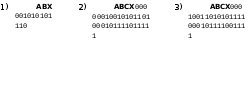
Вариант 3

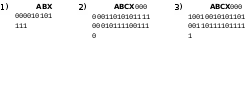
Вариант 4

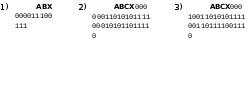
Вариант 5

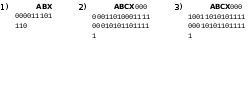
Вариант 6

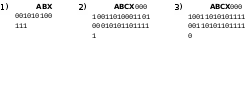
Ответы по вариантам:

Ваpиант 1	Ваpиант 2	Ваpиант 3
Ваpиант 4	Ваpиант 5	Ваpиант 6

3. 
   Построение предикатов

1-4. Задайте с помощью предиката множество точек, соответствующее заштрихованной области на плоскости.

5. Введите предикат и запишите заданное высказывание, используя кванторы.

6. Запишите отрицание высказывания, записанного в п. 5, в словесной форме и с помощью кванторов и введённого предиката.

	Вариант 1	Вариант 2	Вариант 3
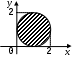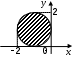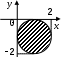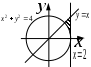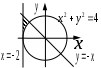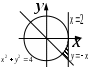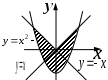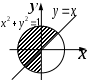	«Для любой реки существует море, в которое она впадает».	«Для любого моря существует река, которая в него впадает».	«Существует река, которая впадает во все моря».

	Вариант 4	Вариант 5	Вариант 6
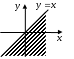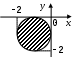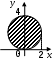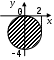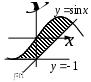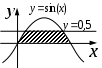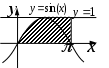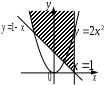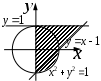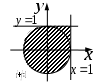	«Существует море, в которое впадают все реки».	«Найдется такая гора, что ни одна птица не может подняться выше неё».	«Для каждой горы найдется птица, которая не может подняться выше неё».

Ответы по вариантам:

Ваpиант 1

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   , где : «река впадает в море »
   
6. 
   «Найдется такая река, для которой не существует моря, в которое она впадает».
   

Ваpиант 2

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   , где : «река впадает в море »
   
6. 
   «Найдётся такое море, для которого нет рек, которые в него впадают».
   
   

Ваpиант 3

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   , где : «река впадает в море »
   
6. 
   «Нет такой реки, которая впадает во все моря».
   
   

Ваpиант 4

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   , где : «река впадает в море »
   
6. 
   «Нет такого моря, в которое впадают все реки».
   
   

Ваpиант 5

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   , где : «птица может подняться выше горы »
   
6. 
   «Не существует такой горы, что ни одна птица не может подняться выше неё».
   
   

Ваpиант 6

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   , где : «птица может подняться выше горы »
   
6. 
   «Существует такая гора, что любая птица может подняться выше неё».
   
   

Самостоятельная работа (дополнительная)
Построение схем на логических элементах

1. 
   Постройте схему, соответствующую заданной логической функции, на логических элементах «И», «ИЛИ» и «НЕ». Предварительно преобразуйте выражение так, чтобы количество использованных логических элементов было минимальным.
   
2. 
   Постройте схему, соответствующую заданной логической функции, на логических элементах «И», «ИЛИ» и «НЕ» (в базисе «И-ИЛИ-НЕ»). Предварительно преобразуйте выражение так, чтобы количество использованных логических элементов было минимальным.
   
3. 
   * Используя формулу (она следует из закона двойного отрицания и закона де Моргана), постройте схему, соответствующую логической функции из п. 1, используя только логические элементы «И-НЕ» (в базисе «И-НЕ»).
   
4. 
   * Используя формулу (она следует из закона двойного отрицания и закона де Моргана), постройте схему, соответствующую логической функции из п. 1, используя только логические элементы «ИЛИ-НЕ» (в базисе «ИЛИ-НЕ»).
   

Вариант 1	Вариант 2
Вариант 3	Вариант 4
Вариант 5	Вариант 6

Ответы по вариантам:

Вариант 1

1. 
   
   
2. 
   
   
3. 
   
   

4. 
   
   

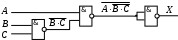
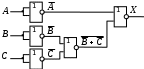
Вариант 2

1. 
   
   
2. 
   
   
3. 
   
   

4. 
   
   

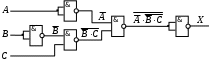
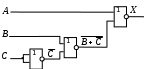
Вариант 3

1. 
   
   
2. 
   
   
3. 
   
   

4. 
   
   

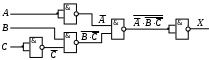
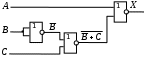
Вариант 4

1. 
   
   
2. 
   
   
3. 
   
   

4. 
   
   

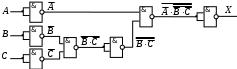
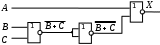
Вариант 5

1. 
   
   
2. 
   
   
3. 
   
   

4. 
   
   

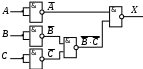
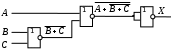
Вариант 6

1. 
   
   
2. 
   
   
3. 
   
   

4. 
   
   

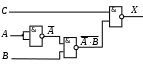
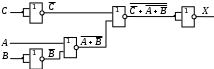
http://kpolyakov.spb.ru