конспект к уроку 7 класса. Графы и их применение. Но я думаю, что прежде всего вам бы хотелось узнать тему сегодняшнего урока
 Скачать 2.55 Mb. Скачать 2.55 Mb.
|
|
Графы и их применение. 1.) Организационный момент -Здравствуйте, ребята! -«математика» - это стройное, красивое здание, по этажам которого вы шагаете с 1-го класса. Сегодня вы пройдёте очередной шаг по дороге знаний, и я с радостью помогу вам сделать этот шаг. -Приготовьте тетрадь к работе, карандаши и линейки. Запишите в тетрадях число (04.04.22), «классная работа» 2.) Тема урока -Но я думаю, что прежде всего вам бы хотелось узнать тему сегодняшнего урока. А для этого давайте мы с вами попробуем отгадать рисунки:    (Параграф) (фотограф) (граффити) -Посмотрите внимательно на слова и давайте попробуем определить, какой слог встречается в каждом слове.? -Правильно – слог «Граф». Как вы думаете, что означает это слово? Какие ассоциации возникают у вас при этом слове? -Но у нас с вами урок математики, поэтому сегодня мы будем разговаривать не про дворянский титул «граф», а про замечательные математические объекты, с помощью которых можно решать много различных задач. В математике существует даже целый раздел «теория графов», который изучает графы, их свойства и применение. Запишем в тетрадях тему урока «Графы» 3.) Определение. Графом называют конечное множество точек, которые соединены отрезками прямых. Точки называются вершинами графа, а отрезки – ребрами графа (рисунок на презентации). -Решим небольшую задачу: У каждого из трех друзей: Васи, Миши, Коли есть свой шалаш. Они решили установить между собой связь с помощью проволочного телефона. Вопрос: какое наименьшее количество линий из проволоки им придется провести, чтобы каждый из них мог поговорить с каждым? (Молодцы! Конечно же 3 линии) -Теперь давайте немного усложним задачу: К трем друзьям присоединился 4 друг (Лёня) и построил свой шалаш. Сколько же линий нужно провести в этом случае? -Давайте попробуем нарисовать эту задачу (рисуем граф). -А теперь посмотрим, что у нас с вами получилось? (6 линий) -Вот на самом деле, мы с вами граф и нарисовали. Ещё раз посмотрите на граф, который у нас получился, такой граф называется неориентированным. Неориентированный граф – это граф. В котором у линий не указаны направления. Так же есть графы ориентированные. Ориентированный граф – это граф, у которых рёбра со стрелками, то есть они указывают направление. Давайте сразу рассмотрим на примере задачи, от прошлой она отличается тем, что граф здесь уже построен и для решения задачи необходимо верно считать все данные. (Задача)  При решении задач с ориентированными графами, не забывайте обращать внимание на то, куда направлены стрелки. Ещё одним видом графов является взвешенный граф. Взвешенный граф - это граф, рёбра которого имеют вес (дополнительную информацию) (рисунок на презентации).   Раздать таблицу  4.) Историческая справка 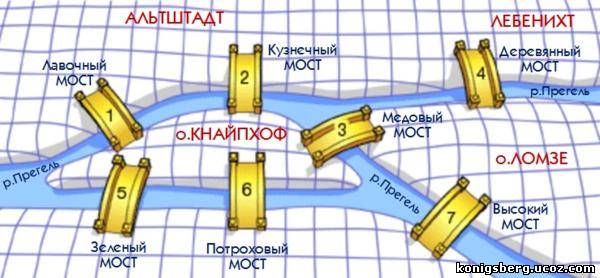 Хронологически первой в теории графов считается задача о семи кенигсбергских мостах. Она состоит в следующем. Парк города Кенигсберга (сейчас этот город называется Калининград) был расположен на обоих берегах реки Прегель и на двух островах. Острова с берегами и друг с другом были соединены семью мостами так, как на рисунке выше. Любимой забавой горожан были поиски такого маршрута, который кончался бы на том же берегу, где и начинался, проходил бы по всем мостам, но по каждому мосту – только один раз. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках - проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог. Разрешить проблему удалось знаменитому математику Леонарду Эйлеру. В 1736 году. Причем, он решил не только эту конкретную задачу, но и придумал общий метод решения подобных задач. -У меня в руках 2 картинки: домик и прямоугольник, в котором проведены диагонали. (раздать листы с картинками) У вас на листочках эти фигуры. Ваша задача: выяснить, можно ли нарисовать эти фигуры, не отрывая карандаш от листа. Кто смог нарисовать эти фигуры? Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Такими графы названы в честь учёного Леонарда Эйлера. Алгоритм решения определить степень каждой вершины; посчитать количество нечётных вершин; сделать выводы: а) заданный обход возможен, если - все вершины чётные (его можно начать с любой вершины); - две вершины нечётные (его нужно начать с одной из нечётных вершин); б) заданный обход невозможен, если нечётных вершин больше двух; 5.)Задача. Можно ли нарисовать эти фигуры, не отрывая карандаш от бумаги. 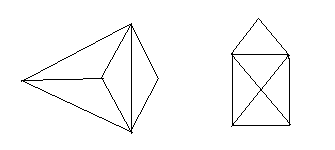  Задача о мостах. Вернёмся к задаче о Кенигсбергских мостах. При решении задачи Эйлер поступил следующим образом: он "сжал" сушу в точки, а мосты "вытянул" в линии.   Решение: Однако число линий для каждой точки на схеме является нечетным. Следовательно, задача не имеет решения. 6.)Примеры графов в жизни: схема метро; генеалогическое древо; кристаллическая решетка; электрическая схема и другие. Придумайте свои примеры графов. (В качестве примеров: схемы железных и автомобильных дорог, тепло- и электросети, дерево каталогов, планы выставок и другие). Так же типичными графами на картах города являются схемы движения городского транспорта, изображения железных дорог, схемы авиалиний, которые часто вывешивается в аэропортах. Графом является и система улиц города. Его вершины – площади и перекрестки, а ребра – улицы. Графы есть и на картах звездного неба.    Графы применяются в различных отраслях науки. Например: А) Графы и история. Историкпрослеживает родословные связи по генеалогическому дереву. Генеалогическое дерево А.С. Пушкина.  Вершины – члены рода, а связывающие их отрезки – отношения родственности. Б) Графы и физика   Инженерчертит схемы электрических цепей. Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем. 7.)РефлексияЧтобы вы могли глубже оценить свою деятельность и вклад в этот урок предлагаю закончить следующие фразы… Сегодня на уроке я узнал… Сегодня на уроке мне понравилось… Сейчас мое настроение …. Задания для самостоятельной работы: 1.)Пятеро студентов обменялись рукопожатиями. Сколько всего было сделано рукопожатий? (10) 2.)На небольшом участке сада растут 7 деревьев: ясень, тополь, ольха, рябина, каштан, липа и сосна. Рябина выше липы, ясень ниже каштана, сосна выше каштана, ольха ниже тополя, но выше сосны, а липа выше тополя. Расположите деревья от самого низкого к самому высокому. Подсказка: используйте ориентированный граф. Стрелки направляйте от более низкого дерева к более высокому. 3.)«Построй» дороги между населёнными пунктами. В таблице указана протяжённость дорог между пунктами (в километрах), через которые можно ехать. Какова длина самого короткого пути от точки А до точки Е? и какова длина самого короткого участка этого пути? Передвигаться можно только по дорогам, указанным в таблице.
|
