лабораторная матлаб. Элементы вектроного анализа. Номер варианта диапазон x
 Скачать 489.69 Kb. Скачать 489.69 Kb.
|
|
Построить графики поверхности для плоского скалярного поля 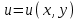 в среде Matlab c помощью команд mesh и surf. Вид функции в среде Matlab c помощью команд mesh и surf. Вид функции 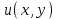 , а также диапазон и шаг изменения переменных , а также диапазон и шаг изменения переменных 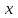 и и  указаны в таблице: указаны в таблице:
 %Задание 1 %Строим поверхности p [X Y]=meshgrid([-1:0.05:2],[-4:0.05:1]); U=X.^2+Y.^2+1; %c помощью команды mesh mesh(X,Y,U); title('График c помощью команды mesh'); xlabel('x'); ylabel('y'); figure(); %c помощью команды surf surf(X,Y,U); title('График c помощью команды surf'); xlabel('x'); ylabel('y'); Листинг программы в Matlab Результат работы 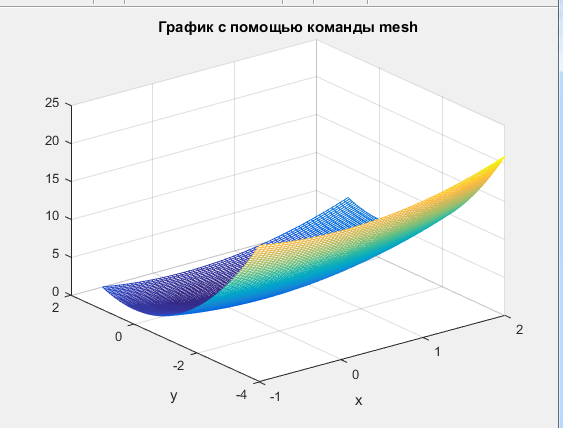 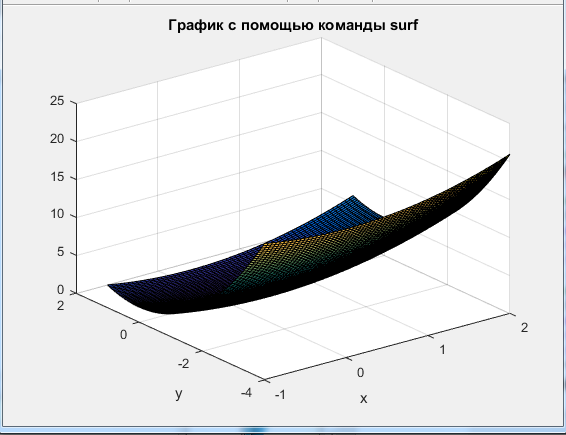 Для скалярного поля из задания 1 рассчитать значение функции, расположенное посередине диапазонов вариации переменных 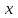 и и  . Построить линию уровня, проходящую через данную точку, с помощью команды contour. . Построить линию уровня, проходящую через данную точку, с помощью команды contour. %Задание 2 %Задаем векторное поле Xmax=2;Xmin=-1;Ymax=1;Ymin=-4 VP = @(x,y) x.^2+y.^2+1; [X Y]=meshgrid([Xmin:0.05:Xmax],[Ymin:0.05:Ymax]); U=VP(X,Y); %Значение функции в серединах вариации переменных x0=(Xmax+Xmin)/2 y0=(Ymax+Ymin)/2 U0=VP(x0,y0); fprintf('Значение функции в середине равно: %5.3f\n',U0); %Строим линию уровня contour(X,Y,U,[U0 U0]) title('Линия уровня через середину'); xlabel('x'); ylabel('y'); Листинг программы в Matlab Результат работы 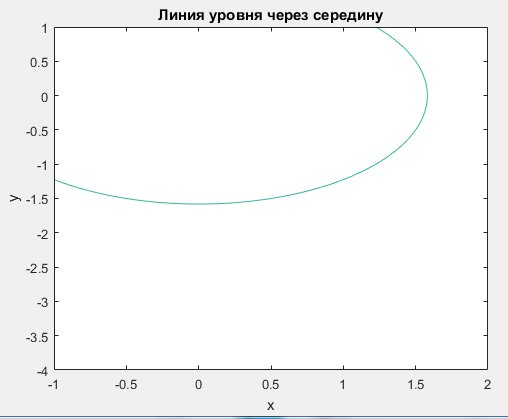 Рассчитать градиент функции скалярного поля из задания 1 в точке из задания 2 численно (аналитически) и с помощью команды gradient (найдя длину вектора градиента по полученным его координатам). Построить вектор указанного градиента совместно с линией уровня (пример - рис. 7).  %Задание 3 %Задаем векторное поле Xmax=2;Xmin=-1;Ymax=1;Ymin=-4 VP = @(x,y) x.^2+y.^2+1; %Значение функции в серединах вариации переменных x0=(Xmax+Xmin)/2 y0=(Ymax+Ymin)/2 U0=VP(x0,y0); %Задание области для градиента dx=0.01;dy=0.01;d=0.1;nx=2*d/dx+1;ny=2*d/dy+1; %XX=linspace(x0-d,x0+d,nx); %YY=linspace(y0-d,y0+d,ny); %Определение номера точки x0 ,y0 nx0=d/dx;ny0=d/dy; %Рассчет матрицы F [XX YY]=meshgrid([x0-d:dx:x0+d],[y0-d:dy:y0+d]); F=VP(XX,YY); %Рассчет матриц производных [FX,FY] = gradient(F,dx,dy); %Значение производных FX0=FX(ny0,nx0) FY0=FX(ny0,nx0) [X Y]=meshgrid([Xmin:0.05:Xmax],[Ymin:0.05:Ymax]); U=VP(X,Y); x0=(Xmax+Xmin)/2 y0=(Ymax+Ymin)/2 U0=VP(x0,y0); %Строим линию уровня contour(X,Y,U,[U0 U0]) title('Линия уровня и градиент'); xlabel('x'); ylabel('y'); grid on hold on plot([x0 FX0],[y0 FY0],'-r'); hold off Листинг программы в Matlab Результат работы  Построить набор векторов плоского векторного поля, заданного координатными функциями 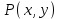 и и 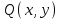 в среде Matlab c помощью команды quiver. Вид функций в среде Matlab c помощью команды quiver. Вид функций 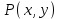 и и 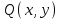 , а также диапазон и шаг изменения переменных , а также диапазон и шаг изменения переменных  и и  указаны в таблице (вектора строятся для каждой точки из диапазона координат): указаны в таблице (вектора строятся для каждой точки из диапазона координат):
 %Задание 4 %Задаем векторное поле P = @(x,y) x; Q = @(x,y) y; x=linspace(1,-1,10); y=linspace(1,-1,10); u=P(x,y); v=Q(x,y); quiver3(x,y,u,v,c); title('Набор векторов плоского векторного поля'); xlabel('x'); ylabel('y'); grid on Листинг программы в Matlab Результат работы 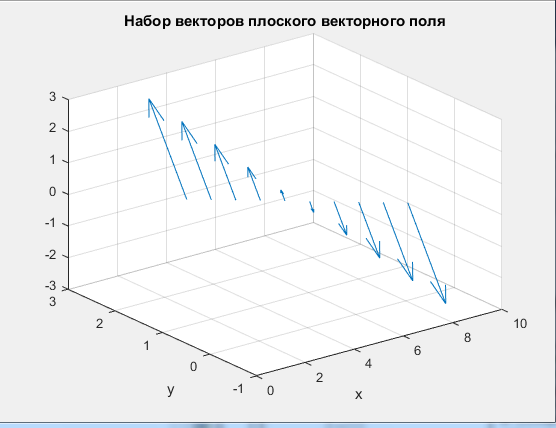 Аналитически найти выражения для семейства векторных линий для плоского векторного поля, заданного координатными функциями 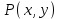 и и 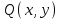 из задания 1. По заданным значениям константы c и массиву значений свободной координаты векторной линии (указаны в таблице) рассчитать массив значений зависимой координаты согласно выражению для векторной линии. По полученным массивам координат построить векторную линию и вектора поля на ней. из задания 1. По заданным значениям константы c и массиву значений свободной координаты векторной линии (указаны в таблице) рассчитать массив значений зависимой координаты согласно выражению для векторной линии. По полученным массивам координат построить векторную линию и вектора поля на ней. Решение Построить векторные линии и для плоского (двумерного) поля  . Построить несколько векторов для данного поля. . Построить несколько векторов для данного поля.По уравнению семейства линий:  Уравнение семейства линий задано в явном виде  %Задание 5 %Задаем векторное поле Xmax=1;Xmin=-1;Ymax=1;Ymin=-1 P = @(x,y) x; Q = @(x,y) y; c=1; Yx = @(x) x*c; x=linspace(0,1,10); y=Yx(x) u=P(x,y); v=Q(x,y); %Строим линию уровня quiver(x,y,u,v,c); title('Векторная линия и вектора поля'); xlabel('x'); ylabel('y'); hold on plot(x,y,'-r'); hold off grid on Листинг программы в Matlab Результат работы 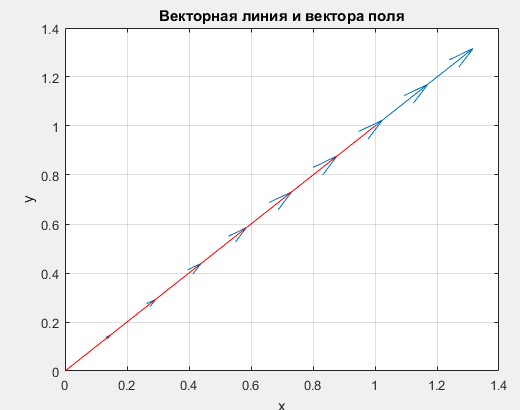 Рассчитать 3-х мерный массив координат векторов для объемного векторного поля, заданного координатными функциями 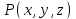 , , 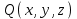 , , 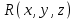 при произвольных и одинаковых диапазонах и шаге вариации переменных при произвольных и одинаковых диапазонах и шаге вариации переменных 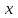 , ,  , ,  . Построить указанные вектора с помощью команды quiver3. . Построить указанные вектора с помощью команды quiver3. %Задание 6 %Задаем векторное поле P = @(x,y,z) -x.^2+z.^2./y; Q = @(x,y,z) y.^2-x.^2+z./y; R = @(x,y,z) z.^2+y.^2./x; x=-2:0.1:2; y=-2:0.1:2; z=-2:0.1:2; u=P(x,y,z); v=Q(x,y,z); w=R(x,y,z); %Строим линию уровня quiver3(x,y,z,u,v,w,10); title('Векторное поле'); grid on Листинг программы в Matlab Результат работы 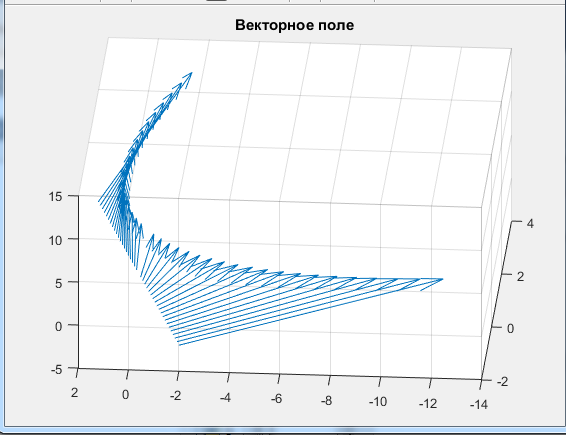 Найти значение дивергенции объемного векторного поля из задания 6 с помощью команды divergence. Построить графики срезов объема в 3-х произвольных плоскостях (команда slice), график поверхности уровня для произвольного значения функции divergence (команда isosurface) и графики срезов с поверхностей уровня в 3-х произвольных плоскостях (команда contourslice).  %Задание 7 %Задаем векторное поле P = @(x,y,z) -x.^2+z.^2./y; Q = @(x,y,z) y.^2-x.^2+z./y; R = @(x,y,z) z.^2+y.^2./x; x=-2:0.1:2; y=-2:0.1:2; z=-2:0.1:2; [U V W]=meshgrid(P(x,y,z),Q(x,y,z),R(z,y,z)); u=P(x,y,z); v=Q(x,y,z); w=R(x,y,z); div = divergence(x,y,z,U,V,W); slice(x,y,z,div,[-2 0 2],[-2 0 2],[-2 0 2]); title('Срезы объема'); figure() isosurface(x,y,x,div,1) title('Поверхность уровня'); figure() contourslice(x,y,z,div,[-2 -1 0 1 2],[-2 -1 0 1 2],[-2 -1 0 1 2],[-2 -1 0 1 2]) title('Графики срезов с поверхностей уровня'); Листинг программы в Matlab Результат работы   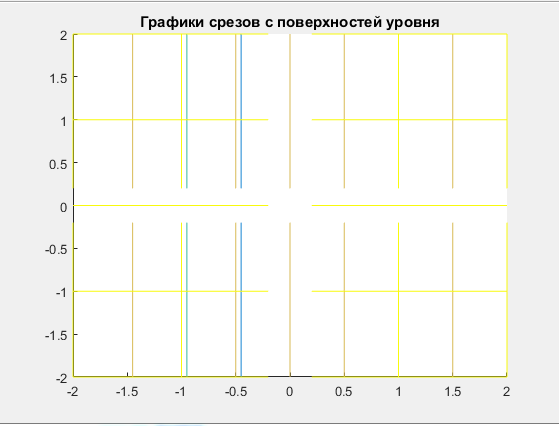 |