Вввв. ответы. Номинативная шкала
 Скачать 256.05 Kb. Скачать 256.05 Kb.
|
|
БИЛЕТ№1 Типы измерительных шкал в психологии Номинативная шкала (номинальная или шкала наименований) [потеп (лат.) - имя, название) - это шкала, классифицирующая по названию и устанавливающая соответствие признака тому или иному классу. Название же не измеряется количественно, оно лишь позволяет отличить один объект от другого или одного субъекта от другого. "мужчина/женщина", "иностранец - соотечественник"; Признак, который изменяется по дихотомической шкале наименований, называется альтернативным. Он может принимать всего два значения. Более сложный вариант номинативной шкалы - классификация из трех и более ячеек Вместо чисел при использовании шкалы наименований можно применять другие символы Разновидностью шкалы наименований является дихотомическая шкала - это шкала классификации, рассматривающаяся как вариант шкалы наименований в случае, когда мы измеряем свойство, имеющее всего лишь два уровня выраженности: "есть-нет", так называемое "точечное" свойство. Порядковая шкала (шкала порядка или ординарная шкала) -это шкала, классифицирующая по принципу "больше - меньше". Здесь субъекты могут быть ранжированы, например, по весу или росту. В порядковой шкале должно быть не менее трех классов, например, "положительная реакция - нейтральная реакция - отрицательная реакция" или "подходит для занятия вакантной должности - подходит с оговорками - не подходит". В порядковой шкале мы не знаем истинного расстояния между классами, а знаем лишь, что они образуют последовательность. Все психологические методы, использующие ранжирование, построены на применении шкалы порядка. шкала порядка позволяет ввести линейную упорядоченность объектов на некоторой оси признака. Тем самым вводится важнейшее понятие - измеряемое свойство, или линейное свойство, тогда как шкала наименований использует неточный вариант интерпретации понятия "свойство", а лишь в контексте - "свойство есть -свойства нет". Переходным вариантом шкалы порядка можно считать дихотомическую классификацию, проводимую по принципу "есть свойство (1) - нет свойства (О)" при 1 > 0. Дихотомическое разбиение множества позволяет применять не только порядок, но и метрику (переход к интервальной шкале). Интервальная шкала (шкала равных интервалов) - это шкала, классифицирующая по принципу "больше на определенное количество единиц - меньше на определенное количество единиц". Шкала интервалов - первая метрическая шкала, определяющая величину различий между объектами в проявлении свойства. Интервальная шкала представляет собой полностью упорядоченный ряд с измеренными интервалами между пунктами, причем отсчет начинается с произвольно выбранной величины. Каждое из возможных значении признака отстоит от другого на равном расстоянии. Таким образом, в шкале интервалов нулевая точка отсчета может устанавливаться произвольно, а величины единиц и направление отсчета могут определяться по избираемым константам. Шкала интервалов имеет масштабную единицу, но положение нуля на ней произвольно Шкала равных отношений - это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности измеряемого свойства. В отличие от интервальной шкалы она имеет значимую нулевую точку, которая не произвольна, а указывает на полное отсутствие измеряемого свойства. В шкалах отношений классы обозначаются числами, которые пропорциональны друг другу (например, 2 так относится к 4, как 4 к 8). Наличие нулевой точки - проблема для большинства психологических переменных. Возможности человеческой психики столь велики, что трудно себе представить абсолютный нуль в какой-либо измеряемой психологической переменной. Абсолютная глупость и абсолютная честность - понятия скорее житейской психологии. Абсолютный нуль, правда, может иметь место при подсчете количества объектов или субъектов Шкала отношений отличается от шкалы интервалов тем, что на ней определено положение "естественного нуля". Классический пример -шкала температур Кельвина. В некоторой степени шкала отношений является идеалом измерительной процедуры. Значения шкалы отношений инвариантны относительно преобразования вида: х1 = ах. Значения шкалы можно умножать на константу. К ним применимы любые статистические меры. Измерения массы, времени реакции и выполнения тестового задания - таковы области применения шкалы отношений. Отличием этой шкалы от абсолютной является отсутствие "естественной" масштабной единицы. Кроме перечисленных видов шкал ряд специалистов выделяют также абсолютную шкалу и шкалу разностей. Шкала разностей, в отличие от шкалы отношений, не имеет естественного нуля, но имеет естественную масштабную единицу измерения. Ей соответствует аддитивная группа действительных чисел. Классическим примером этой шкалы является историческая хронология. Она сходна со шкалой интервалов. Разница лишь в том, что значения этой шкалы нельзяумножать (делить) на константу. Поэтому считается, что шкала разностей - единственная с точностью до сдвига. Абсолютная шкала является развитием шкалы отношений и отличается от нее тем, что обладает естественной единицей измерения. В этом ее сходство со шкалой разностей. Число решенных задач ("сырой" балл), если задачи эквивалентны, одно из проявлений абсолютной шкалы. БИЛЕТ№2 Стандартные шкалы и стандартизация 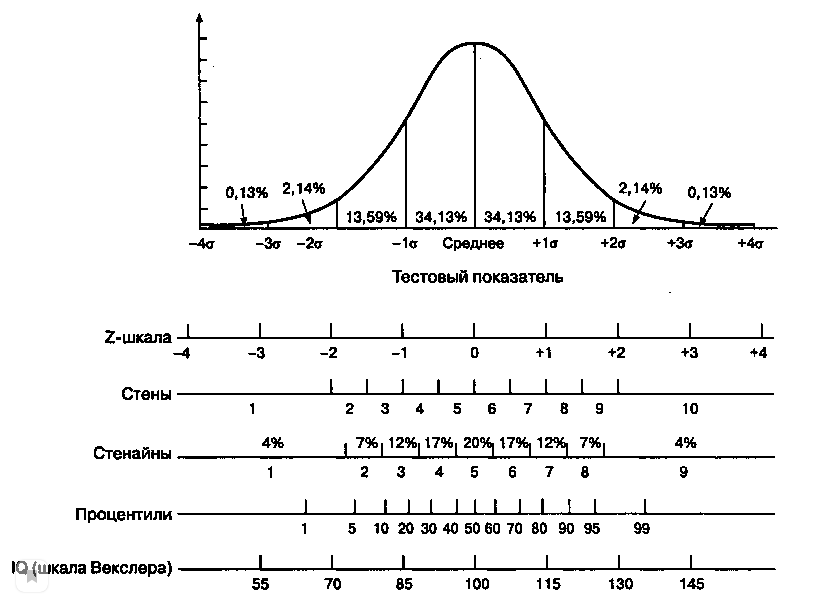 Стандартизация (преобразование) данных – перевод измерений в стандартную z-шкалу, где Мz =0, Дz =1. Формула перевода в z-шкалу : Перевод в стандартную шкалу: Sc=(Z*A)+M, где A – заданное стандартное отклонение, M – заданное среднее значение. Т-шкала Маккола: М = 50; А = 10; шкала IQ (коэффициент интеллектуальности): М = 100; А = 15; шкала стенов (стандартная десятка): М=5,5; А= 2,0; шкала стэнайнов (целочисленные значения от 1 до 9 – стандартная девятка): М = 5,0; А = 2.  БИЛЕТ№3 Меры центральной тенденции Мера центральной тенденции (Central Tendency) — это число, характеризующее выборку по уровню выраженности измеренного признака. Мода (Mode) — наиболее часто встречающееся значение в ряду данных. Среди 8 значений признака (3, 7, 3, 5, 7, 8, 7, 6) мода Мо=7 как наиболее часто встречающееся значение. Медиана (Me, Md) – «серединное значение» после упорядочивания всех выборочных значений переменной по возрастанию• если данные содержат нечетное число значений (8, 9,10,13,15), то медиана есть центральное значение, т. е. Md = 10;• если данные содержат четное число значений (5, 8, 9, 11), то медиана есть точка, лежащая посередине между двумя центральными значениями, т. е. Md= (8+9)/2=8,5. Среднее значение – это показатель, который используется для измерения центра или середины в наборе числовых данных. Среднее значение – сумма всех чисел, деленная на общее количество чисел. Сравнивать между собой две выборки по среднему арифметическому можно при соблюдении ряда условий: Достаточно большие по объему группы, чтобы судить о форме распределения; Распределения симметричны; Отсутствуют «выбросы». Если хотя бы 1-но из условий не выполняется, используют Мо, Ме. Альтернатива: ранжирование сравниваемых групп и сравнение средних, вычисленных для рангов этих групп. Билет№4 Меры изменчивости признака. Меры центральной тенденции отражают уровень выраженности измеряемого признака. Меры изменчивости применяются для численного выражения величины межиндивидуальной вариации признака. Меры изменчивости: Размах – разность максимального и минимального значения Дисперсия – мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений, измеренных значений от их среднего арифметического Стандартное значение – это среднее расстояние от среднего значения. Стандартное отклонение – это способ, с помощью которого статистики измеряют степень изменчивости (разброса или рассеяния) чисел в наборе данных. Асимметрия – степень отклонения графика распределения частот от симметричного вида относительно среднего арифметического. БИЛЕТ№5 Кривая нормального распределение. Целесообразность применения в психологии. Кривая нормального распределения – это модель, представляющая собой абсолютно симметричное и гладкое распределение данных, представляет форму колокола, и имеет следующие свойства: единица измерения является стандартное отклонение, кривая приближается к оси асимптотически и никогда не касается ее, симметрично относительно среднего значения (равного нулю). Применим в психологии по следующим причинам:Разработка тестовых шкал: разработка такой шкалы, в которой распределение тестовых показателей в стандартизации соответствовало бы нормальному распределению.Проверка нормальности выборочного распределения, для принятия решения о том, в какой шкале измерен признак – в метрической или порядковой. Так как к метрической шкале применимы практически любые математические методы анализа данных, тогда как к порядковой применим только метод ранжирования данных по количеству или качеству признака, но не позволяет сказать «насколько одна величина больше другой». Если перевести данные в гистограмму, и она напоминает колокол, то это метрическая шкала.Статистическая проверка гипотез. Если перевести данные выборки в гистограмму, и она напоминает кривую нормального распределения, то это даст предположить, что генеральная совокупность распределена нормально, и гипотеза верна. Билет№ 6 Виды статистических гипотез Статистические гипотезы делятся на два вида – нулевую и альтернативную, в зависимости от статистического метода. Альтернативная гипотеза является отрицанием нулевой гипотезы.  Билет№7. Уровень статистической значимости, зоны значимости, основания для принятия статистического вывода. Уровень значимости – это вероятность того, что исследователь счел различия существенными, а они на самом деле случайны. Когда мы указываем, что различия достоверны на 5%-ом уровне значимости, или при р<0,05, то мы имеем виду, что вероятность того, что они все-таки недостоверны, составляет 0,05 (или 0,05·100%=5%). Когда мы указываем, что различия достоверны на 1%-ом уровне значимости, или при р<0,01, то мы имеем в виду, что вероятность того, что они все-таки недостоверны, составляет 0,01. Уровень значимости – это вероятность отклонения нулевой гипотезы, в то время как она верна. Ошибка, состоящая в том, что мы отклонили нулевую гипотезу, в то время как она верна, называется ошибкой 1 рода. Если вероятность ошибки – это α, то вероятность правильного решения: 1–α. Чем меньше α, тем больше вероятность правильного решения До тех пор, однако, пока уровень статистической значимости не достигнет р=0,05, мы еще не имеем права отклонить нулевую гипотезу. Правило отклонения H0 и принятия Н1. Если эмпирическое значение критерия равняется критическому значению, соответствующему р<0,05 или превышает его, то H0 отклоняется, но мы еще не можем определенно принять H1. Если эмпирическое значение критерия равняется критическому значению, соответствующему р<0,01 или превышает его, то Н0 отклоняется и принимается H1. Исключения: критерий знаков G, критерий Т Вилкоксона и критерий U Манна-Уитни. Для них устанавливаются обратные соотношения. Практически, однако, исследователь может считать достоверными уже те различия, которые не попадают в зону незначимости, заявив, что они статистически значимы при р<0,05, или указав точный уровень значимости полученного эмпирического значения критерия, например: р=0,02. Формулирование гипотез систематизирует предположения исследователя и представляет их в четком и лаконичном виде. Статистические гипотезы подразделяются на нулевые и альтернативные, направленные и ненаправленные. Нулевая гипотеза – это гипотеза об отсутствии различий или значимых связей. Она обозначается как H0 и называется нулевой потому, что содержит число 0: X1 – Х2 = 0, где Х1, X2 – сопоставляемые значения признаков. Нулевая гипотеза – это то, что мы хотим опровергнуть, если перед нами стоит задача доказать значимость различий. Альтернативная гипотеза – это гипотеза о значимости различий. Она обозначается как Н1. Чаще в исследованиях требуется доказать наличие статистически значимых различий. Однако, бывают задачи, когда желательно доказать как раз отсутствие статистической значимости различий, то есть подтвердить нулевую гипотезу, – например, если исследователю нужно убедиться, что разные испытуемые получают хотя и различные, но уравновешенные по трудности задания, или что экспериментальная и контрольная выборки не различаются между собой по каким-то характеристикам помимо исследуемого фактора. Нулевая и альтернативная гипотезы могут быть направленными и ненаправленными. Билет№8 Параметрические критерии: основания для их выбора, порядок расчета и интерпретации. Чаще основаны на нормальном распределении результатов выборки (генеральной совокупности); обладают большей мощностью в сравнении с непараметрическими. F-критерий Фишера, t-критерий Стьюдента, критерий Уэлча, критерий Крамера Параметрические критерии включают в формулу расчета параметры распределения, то есть средние и дисперсии (t-критерий Стьюдента, критерий F Фишера и др.) Параметрические критерии могут более мощными; чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. С интервальной шкалой есть определенные проблемы. Лишь с некоторой натяжкой мы можем считать данные, представленные не в стандартизованных оценках, как интервальные. Кроме того, проверка распределения на нормальность требует достаточно сложных расчетов, результат которых заранее неизвестен. Может оказаться, что распределение признака отличается от нормального, и нам так или иначе все равно придется обратиться к непараметрическим критериям. Параметрический F-критерий Фишера Условия для применения критерия: Измерение должно быть проведено в шкале интервалов или отношений. Сравниваемые выборки должны быть распределены по нормальному закону. Основные задачи: Проверка гипотезы о различии дисперсий двух сравниваемых выборок. Проверка гипотезы о равенстве дисперсии двух выборок. Билет№ 9 Непараметрические критерии: основания для их выбора, порядок расчета и интерпретации. Критерии различия на базируются на нормальном распределении (называются также критериями свободными от распределения). Менее трудоемки в расчетах, чем параметрические. ϕ-критерий Фишера, критерий знаков G, критерий Макнамары, Н-критерий Крускала-Уоллиса, критерий Хи-квадрат (χ²) Непараметрические критерии лишены всех этих ограничений, и не требуют таких длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены лишь в одном - с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака. Эту задачу может решить только дисперсионный двухфакторный анализ. В большинстве случаев для того, чтобы мы признали различия статистически значимыми, необходимо, чтобы эмпирическое значение критерия превышало критическое, хотя есть критерии (например, критерий Манна-Уитни или критерий знаков), в которых мы должны придерживаться противоположного правила. В некоторых случаях расчетная формула критерия включает в себя количество наблюдений в исследуемой выборке, обозначаемое как n. В этом случае эмпирическое значение критерия одновременно является тестом для проверки статистических гипотез. По специальной таблице вручную мы определяем, какому уровню статистической значимости различий соответствует данная эмпирическая величина. Примером такого критерия является t-критерий Стьюдента. Или компьютерный пакет выдает уровень статистической значимости. В большинстве случаев, однако, одно и то же эмпирическое значение критерия может оказаться значимым или незначимым в зависимости от количества наблюдений в исследуемой выборке (n) или от так называемого количества степеней свободы, которое обозначается как ν или как df. Для каждого случая определение количества степеней свободы имеет свою специфику, поэтому каждая формула для расчета эмпирического значения критерия обязательно сопровождается правилом (формулой) для определения числа степеней свободы. Зная n и/или число степеней свободы, мы по специальным таблицам можем определить критические значения критерия и сопоставить с ними полученное эмпирическое значение. Условия для применения ϕ-критерий Фишера: Измерение может быть проведено в любой шкале. Характеристики выборок могут быть любыми. Нижняя граница в одной из выборок может быть 2 наблюдения, но во второй не менее 30 наблюдений. Верхняя граница не определена. Нижние границы двух выборок должны быть не меньше 5 наблюдений в каждой. 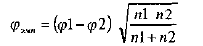 ϕ1 – величина с большей процентной долей (берется в табл. критич. знач. ϕ-критерия), ϕ2 – величина с меньшей процентной долей, n1 – количество наблюдений в первой выборке, n2 – количество наблюдений во второй выборке Билет№ 10.Виды коэффициентов корреляции. Основания для выбора критерия, его расчет. Коэффициент корреляции – это мера прямой или обратной пропорциональности между двумя переменными. «Корреляция» - в прямом переводе «соотношение». Коэффициент ранговой корреляции Спирмена ∑d² – разность рангов, N – объем выборки, количество исследуемых признаков Условия для применения критерия: Сравниваемые переменные должны быть получены в ранговой (порядковой) шкале, но могут быть измерены в шкале интервалов и в шкале отношений. Характер распределения величин не имеет значения. Число врьируемых признаков в сравниваемых выборках должно быть одинаковым. к=n Коэффициент линейной корреляции Пирсона Мх – среднее арифметическое по выборке х, Му – среднее арифметическое по выборке у, 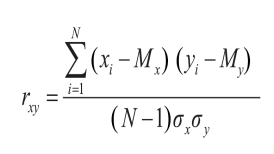 N – число признаков, Ϭ – стандартное отклонение. Условия для применения критерия: Сравниваемые переменные должны быть измерены в интервальной шкале или шкале отношений. Распределения исследуемых переменных должны быть близки к нормальным. Число признаков в выборках должно быть одинаковым. к=n–2, к – число степеней свободы – количество возможных изменений направлений признака, минус число условий, при которых он был сформирован Фи-коэффициент (коэффициент ассоциации) Арифметический аналог критерия Пирсона для бинарных данных. Условия применения критерия: Сравниваемые признаки измерены в дихотомической шкале. Число сравниваемых признаков должно быть одинаковым. к=n–2 Для расчета уровня достоверности следует использовать формулу: Тϕ=|r(эмп)|*√(n–2)/(1–r (эмп)²), где n – число коррелируемых признаков, r(эмп) – коэффициент корреляции, полученный эмпирическим путем. Тϕ сравнивается с табл. критических значений Стьюдента. |
