Нормальных уравнений
 Скачать 75.05 Kb. Скачать 75.05 Kb.
|
|
3. Система нормальных уравнений. a*n + b*∑x = ∑y a*∑x + b*∑x2 = ∑y*x Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
Для наших данных система уравнений имеет вид 22a + 709.75*b = 36.061 709.75*a + 28312.848*b = 1231.785 Домножим уравнение (1) системы на (-32.261), получим систему, которую решим методом алгебраического сложения. -709.75a -22897.245 b = -1163.372 709.75*a + 28312.848*b = 1231.785 Получаем: 5415.603*b = 68.412 Откуда b = 0.01263 Теперь найдем коэффициент «a» из уравнения (1): 22a + 709.75*b = 36.061 22a + 709.75*0.01263 = 36.061 22a = 27.097 a = 1.2317 Получаем эмпирические коэффициенты регрессии: b = 0.01263, a = 1.2317 Уравнение регрессии (эмпирическое уравнение регрессии): y = 101.23166805e0.01263x = 17.04779e0.01263x Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. 4.
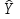 =5,828713+ =5,828713+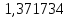 0,396937 0,396937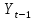 ; ;Сдвигаем исходный ряд на 1 уровней. Получаем следующую таблицу:
Расчет коэффициента автокорреляции 1-го порядка. Параметры уравнения авторегрессии. Выборочные средние. Выборочные дисперсии: Среднеквадратическое отклонение. Коэффициент автокорреляции. Линейный коэффициент автокорреляции rt,t-1: Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < rt,t-1 < 0.3: слабая; 0.3 < rt,t-1 < 0.5: умеренная; 0.5 < rt,t-1 < 0.7: заметная; 0.7 < rt,t-1 < 0.9: высокая; 0.9 < rt,t-1 < 1: весьма высокая; В нашем примере связь между рядами - слабая и обратная.
Значимость коэффициента автокорреляции. 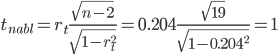 По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=19 находим tкрит: tкрит (n-m-1;α/2) = (19;0.025) = 2.093 где m = 1 - количество объясняющих переменных. Если tнабл > tкритич, то полученное значение коэффициента автокорреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента автокорреляции, отвергается). Поскольку tнабл < tкрит, то принимаем гипотезу о равенстве 0 коэффициента автокорреляции. Другими словами, коэффициент автокорреляции статистически - не значим Интервальная оценка для коэффициента автокорреляции (доверительный интервал). Доверительный интервал для коэффициента корреляции r(-0.64;0.23)
Вывод: в данном ряду динамики тенденции не наблюдается (rt,t-1 = -0.204 → 0) Самый подходящий модель это Модель множественной линейной регрессии вида 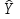 = =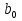 + +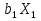 + +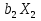 ; ; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
