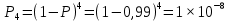НТС. НТС-1 Искаков. новосибирский государственный технический университет
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ образовательное учреждение высшего образования «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» _________________________________________________________________ Кафедра газодинамических импульсных устройств  Расчетно-графическая работа по дисциплине: «Надежность технических систем и техногенный риск» Вариант 0 Выполнил:Проверил: Студент гр. СЭ-81, ФЛА Ассистент Искаков Н.Р. Зубашевский К.М. «___» ______ 2021 г.«___» ______ 2021 г. _______________ _________________ (подпись) (подпись) Новосибирск 2021 ОглавлениеЗадача 1: Последовательное и параллельное соединения. 3 Задача 2: Мажоритарные системы. 5 Задача 3: Мостиковая система. 7 Задача 4: Однородная Марковская цепь. 9 Задача 5: Марковский процесс с дискретным состоянием и непрерывным временем. 11 Задача 6: Процесс гибели и размножения. 13 Задача 7: Циклический процесс. 15 Вывод 18 Задача 1: Последовательное и параллельное соединения.Вероятность безотказной работы элемента Р=0,99. Все элементы равно надежны. а) Последовательно-параллельное соединение: 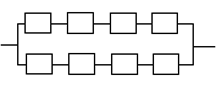 Р2=1-(1- Рn)*(1- Рn) =1-(1-0,9606)*(1-0,9606) =1-0,03942 =0,9984 Р2=1-(1- Рn)*(1- Рn) =1-(1-0,9606)*(1-0,9606) =1-0,03942 =0,9984 Р3 =1-(1- Рn)*(1- Рn)*(1- Рn) =1-0,03943 =1-0,00006 =0,99994 Р3 =1-(1- Рn)*(1- Рn)*(1- Рn) =1-0,03943 =1-0,00006 =0,99994 Р4=1-(1- Рn)*(1- Рn)*(1- Рn)*(1- Рn) =1-0,03944 =0,999998 Р4=1-(1- Рn)*(1- Рn)*(1- Рn)*(1- Рn) =1-0,03944 =0,999998б) Параллельно-последовательное соединение:  P1 = [1-(1-P)*(1-P)]n =[1-(1-0,99)*(1-0,99)]4 =0,9996 P1 = [1-(1-P)*(1-P)]n =[1-(1-0,99)*(1-0,99)]4 =0,9996 P2 = [1-(1-P) *(1-P) *(1-P)]n =0,999996 P2 = [1-(1-P) *(1-P) *(1-P)]n =0,999996 P3 = [1-(1-P)*(1-P) *(1-P) *(1-P)]n = 0,99999 P3 = [1-(1-P)*(1-P) *(1-P) *(1-P)]n = 0,99999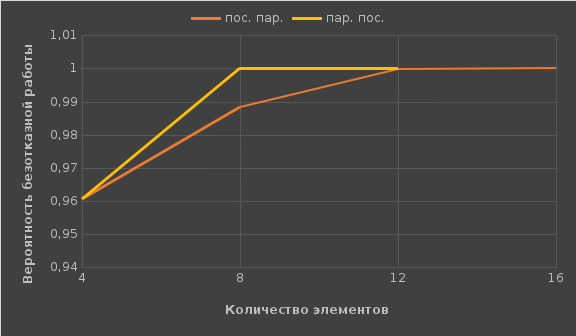 Рис.1 Зависимость вероятности безотказной работы от ее элементов. Вывод: Вероятность безотказной работы системы с увеличением числа элементов растёт. Вероятность безотказной работы системы при параллельно-последовательном резервировании элементов выше, чем при последовательно-параллельном резервировании, что позволяет при одинаковой вероятности безотказной работы уменьшить число элементов резервирования. Задача 2: Мажоритарные системы. Мажоритарная система «3 из 4». Система работоспособна, когда из четырёх её элементов любые три или все четыре работоспособны. Мажоритарная система «3 из 4». Система работоспособна, когда из четырёх её элементов любые три или все четыре работоспособны. р=0,99 Первый метод: Метод прямого перебора:
P=  = =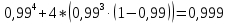 4 4Второй метод: Комбинаторный метод:  m≤k≤n m≤k≤n 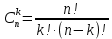    0,9606 0,9606  0,9606=0,9994 0,9606=0,9994Вывод: При расчете работоспособности двумя методами, получили идентичные значения, что говорит о правильности решения. Вероятность безотказной работы всей системы больше таковой для одного элемента, в 1,01 раз. Задача 3: Мостиковая система.р=0,99. 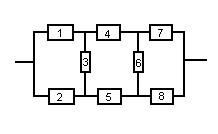 Метод 1: метод минимальных сечений. 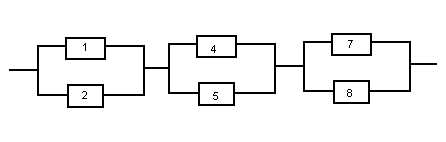 Минимальными сечениями системы называются совокупности минимального набора элементов, одновременные отказы которых приводят к отказу всей системы. Минимальными сечениями системы называются совокупности минимального набора элементов, одновременные отказы которых приводят к отказу всей системы.Рэ=(1-(1-Р)2)3=(1-(1-0,99)2)3=0,9997 М 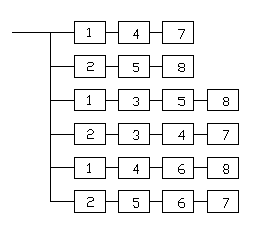 етод 2: метод минимальных путей. етод 2: метод минимальных путей.Минимальный путь — это множество элементов системы, работоспособность которых необходима и достаточна для работоспособности системы. Рэ=1-(1-Р3)2*(1-Р4)4=1-(1-0,993)2*(1-0,994)4=0,999999997 Метод 3: метод разложения относительно особого элемента. Этот метод основан на теореме математической логики о разложении функции по любому аргументу, которая может быть сформулирована следующим образом: P  =PiPjP(pi=1, pj=1)+ PiqjP(pi=1, pj=0)+ qiPjP(pi=0, pj=1)+ qiqjP(pi=0, pj=0). =PiPjP(pi=1, pj=1)+ PiqjP(pi=1, pj=0)+ qiPjP(pi=0, pj=1)+ qiqjP(pi=0, pj=0).P(pi=1, pj=1) Рэ=(1-(1-Р)2)3=(1-(1-0,99)2)3=0,9997. P  (pi=1, pj=0) (pi=1, pj=0)Р1=1-(1-Р)2=1-(1-0,99)2=0,9999 Р2=1-(1-Р2)2=1-(1-0,992)2=0,9996 Рэ=Р1*Р2=0,9999*0,9996=0,9995 P  (pi=0, pj=1) (pi=0, pj=1) Р1=1-(1-Р2)2=1-(1-0,992)2=0,9996 Р2=1-(1-Р)2=1-(1-0,99)2=0,9999 Рэ=Р1*Р2=0,9996*0,9999=0,9995 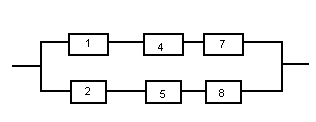 P(pi=0, pj=0) Рэ=(1-(1-Р)3)2=(1-(1-0,99)3)2=0,999998 Р= 0,99*0,99*0,9997 + 0,99 * 0,01 * 0,9995 * 2 + 0,01 * 0,01 * 0,999998= 0,9997 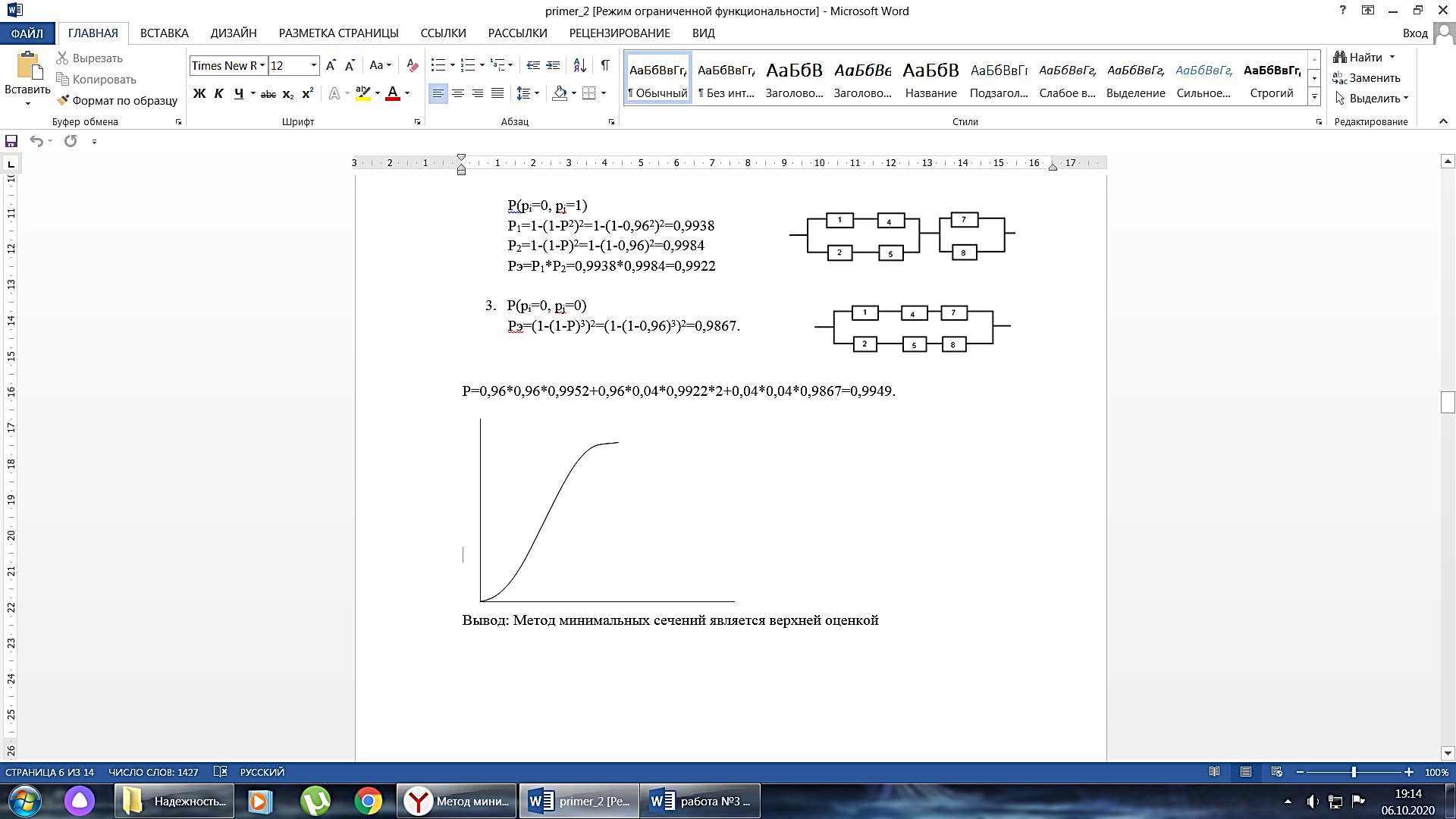 Вывод: Метод минимальных сечений является верхней оценкой. Задача 4: Однородная Марковская цепь. Где Р=0,32 Марковская цепь считается однородной, если переходные вероятности не зависят от номера шага. По некоторой цели ведётся стрельба четырьмя выстрелами в момент времени t1, t2, t3, t4. Возможны следующие состояния системы: S1 – цель невредима; S2 – незначительные повреждения; S3 – цель получила существенные повреждения; S4 - цель поражена. Размеченный граф состояний системы, показан на рисунке. В начальный момент цель находится в состоянии S1 . Определить вероятности состояний цели после четырёх выстрелов.  Так как в начальный момент цель S находится в состоянии S1, то р1(0)=1. Вероятности состояний после первого шага берутся из первой строки матрицы: р1(1)=0,38; р2(1)=0,32; р3(1)=0,2; р4(1)=0,1. Вероятности состояний после второго шага: Р1(2)=р1(1)Р11= 0,38*0,38= 0,1444; Р2(2)=р1(1)Р12+ р2(1)Р22= 0,38*0,32+0,32*0,2= 0,1856; Р3(2)=р1(1)Р13+ р2(1)Р23+ р3(1)Р33= 0,38*0,2+0,32*0,5+0,2*0,2= 0,276; Р4(2)=р1(1)Р14+ р2(1)Р24+ р3(1)Р34+ р4(1)Р44= 0,38*0,1+0,32*0,3+0,2*0,8+0,1*1= 0,394. Вероятности состояний после третьего шага: Р1(3)= р1(2)Р11= 0,1444*0,38= 0,054872; Р2(3)= р1(2)Р12+ р2(2)Р22= 0,1444*0,32+0,1856*0,2= 0,083328; Р3(3)= р1(2)Р13+ р2(2)Р23+ р3(2)Р33= 0,1444*0,2+0,1856*0,5+0,276 *0,2= 0,17688; Р4(3)= р1(2)Р14+ р2(2)Р24+ р3(2)Р34+ р4(2)Р44= 0,1444 *0,1+0,1856*0,3+0,276*0,8+0,394*1= = 0,68492. Вероятности состояний после четвёртого шага: Р1(4)=р1(3)Р11= 0,054872*0,38= 0,02085136; Р2(4)=р1(3)Р12+ р2(3)Р22= 0,054872*0,32+0,083328*0,2= 0,03422464; Р3(4)=р1(3)Р13+ р2(3)Р23+ р3(3)Р33= 0,054872*0,2+ 0,083328*0,5+0,17688*0,2=0,0880144; Р4(4)=р1(3)Р14+ р2(3)Р24+ р3(3)Р34+ р4(3)Р44= 0,054872*0,1+0,083328*0,3+0,17688*0,8+0,68492*1=0,8569096. Вывод: В данной работе была рассмотрена однородная Марковская цепь, для которой вероятности перехода от шага к шагу не изменяются. Было выявлено, что с увеличением количества шагов, вероятность нахождения системы в конечном состоянии увеличивается. Задача 5: Марковский процесс с дискретным состоянием и непрерывным временем.Состояния системы: S1 – система выполняет свои функции; S2 – система простаивает; S3 – система вышла из строя; S4 – система осматривается; S5 – проведение технического обслуживания 1; S6 - проведение технического обслуживания 2; S7 – текущий ремонт системы; S8 – капитальный ремонт системы; S9 – система списана. Переход системы S из состояния в состояние может осуществляться в любой момент времени. Задание: построить граф состояния и разметить его, записать дифференциальные уравнения Колмогорова. Решение: Граф состояния системы будет выглядеть следующим образом:                Обозначим Pi(t) – вероятность того, что в момент t система S будет находиться в состоянии Si. Найдём вероятность того, что в момент t система S будет находиться в состоянии S1. Придадим t малое приращение  t и найдём вероятность того, что в момент t+ t и найдём вероятность того, что в момент t+ t система будет находиться в состоянии S1. t система будет находиться в состоянии S1. . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S2.  . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S3.  . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S4.  . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S5.  . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S6. 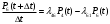 . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S7.  . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S8.  . .Найдём вероятность того, что в момент t система S будет находиться в состоянии S9.  . .Вывод: Интегрирование этой системы уравнений даст нам искомые вероятности состояний, как функции времени. Начальные условия берутся в зависимости от того, каково было начальное состояние системы. Задача 6: Процесс гибели и размножения.Марковская непрерывная цепь называется «процессом гибели и размножения», если все состояния системы можно вытянуть в одну цепочку, в которой каждое из средних состояний связано прямой и обратной связью с каждой из соседских состояний. Техническое устройство состоит их трёх одинаковых узлов; каждый из них может выходить из строя; отказавший узел немедленно начинает восстанавливаться. Состояния системы нумеруется по числу неисправных узлов: S1 – все три узла исправны; S2 – один узел отказал и восстанавливается, два исправны; S3 –два узла отказало и восстанавливаются, один исправен; S4 – все три узла восстанавливаются.  Где Р=1 Найти предельные вероятности состояний. Решение: =  *Р1 *Р1 Все вероятности выражены через Р1. Подставим эти выражения в нормировочное условие: Р1+Р2+Р3+Р4=1. Получим:   Выразим Р1: Выразим Р1: =  = =  Р2=  *Р1= *Р1=  , ,Р3=  *Р2 = *Р2 =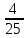 , ,Р4=  Р3= Р3= Проверка:  + + = = =1 =1Задача 7: Циклический процесс.ЭВМ может находиться в следующих состояниях: S1 – система работает; S2 – система неисправна, остановлена, ведётся поиск неисправности; S3 – неисправность оказалась незначительной и устраняется местными средствами; S4 – неисправность оказалась серьёзной и устраняется бригадой специалистов; S5 – подготовка системы к пуску. Требуется найти предельные вероятности состояний и определить средний расход, идущий на оплату работы ремонтной бригады в единицу времени (в сутки). Решение: Строим размеченный граф состояний.  Если из состояния выходит только одна стрелка, то интенсивность потока событий, стоящая у этой стрелки, равна единице, деленной на среднее время пребывания в этом состоянии. Если из состояния выходит две стрелки, то общая интенсивность равна единице, деленной на среднее время пребывания в данном состоянии, умножается для каждой стрелки на вероятность того, что переход совершается именно по этой стрелке. Среднее время пребывания системы в состоянии Si (если она в нём уже находится) равно ti=1/λi, i+1. Уравнение для предельных вероятностей состояний имеют вид:  Нормировочное условие:  . .Из уравнения для предельных вероятностей состояний одно, как мы знаем можно отбросить; отбросим самое сложное – четвёртое, а из остальных выразим Р1: 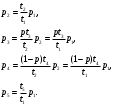 Подставляя полученные выражения в нормировочное уравнение, имеем: 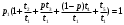 . .Отсюда: 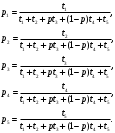 Средняя доля времени, которую система проводит в состоянии S4 равна  . Значит за час, система проводит в этом состоянии в среднем . Значит за час, система проводит в этом состоянии в среднем  часов. Умножая эту величину на 24k, получим средний расход средств на оплату бригады специалистов за сутки: С=24 k часов. Умножая эту величину на 24k, получим средний расход средств на оплату бригады специалистов за сутки: С=24 k . .ВыводНаучились решать задичи по темам: Последовательное и параллельное соединения; Мажоритарные системы; Мостиковая система; Однородная Марковская цепь; Марковский процесс с дискретным состоянием и непрерывным временем; Процесс гибели и размножения; Циклический процесс. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 =
= 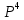 =
= =0,9606
=0,9606